Introduction

Groundwater is one the most crucial resources that supply the water needs of human beings in different parts and zones (Das and Eldho 2022). As groundwater resources are laboriously renewable in nature and the renewing process takes a lot of time and money, a comprehensive plan must be sketched in a way that exploitation carry out in a proper and efficient manner.

Since groundwater resources are the only available sources of freshwater especially in arid zones, their behavior must be investigated and predicted accurately. For this purpose, simulation of groundwater flows in aquifers is a key work that must be considered for all the aquifers. In order to have a pervasive-accurate model, parameters of aquifers have a considerable role (Swathi and Eldho 2014). Therefore, there is a big need to have the parameters of aquifers in precise state.

It is extremely vital to analytically examine the aquifer parameters including transmissivity, hydraulic conductivity, and specific yield (Thomas et al. 2018). As there is no analytical model for groundwater flow just for some simple cases (Mategaonkar and Eldiho 2011), usage of numerical methods is recommended. These methods with linking to some other methods comprise an inverse modeling for aquifer parameter estimation.

The complicated groundwater flow can be analyzed by solving the governing equations with using numerical methods including analytical element method (AEM), finite element method (FEM), finite difference method (FDM), or boundary element method (BEM) (Mategaonkar and Eldho 2011).

As we mentioned before, there is no analytical solution for groundwater flow, using analytical element method (AEM) for estimating transient flow conditions is not satisfying and recommending. The aquifer system is mostly illustrated by a PDE which usually is studied using numerical methods such as FDM and FEM (Pinder and William 2013). Nevertheless, these methods have intrinsic drawbacks based on grids connected by mesh in a predetermined manner like significant expenses in creating grid, less-accurate estimations, and difficulty in adaptive analysis (Swathi and Eldho 2013). By using FDM and FEM solutions, a grid shapes over the domains and a tiresome preprocessing must be performed (Thomas et al. 2012). Numerical solutions, like FDM and FEM, have been applied to the majority of field problems (Wang and Anderson 1995).

There are many researches which used FDM and FEM for simulation of groundwaters. Panahi et al. (2016) used MODFLOW in order to investigate groundwater fluctuations in Zanjan aquifer. They estimated volume of aquifer and found it around 357 MCM. They have also used PEST for calibration of aquifer parameters. Abdelhalim et al. (2019) investigated the more extraction of groundwater from Egypt country on aquifer with MODFLOW. They considered some scenarios. They noted that if the extraction would increase about 25–50 percent, 38 thousand cubic meters would reduce from stored water daily.

Ansarifar et al. (2019) carried out a modeling for groundwater in a coastal aquifer named Bandar-Gaz with MODFLOW. The simulation was carried out on two steady and unsteady states. Their research showed the effect of sea level on hydraulic behavior of coastal aquifer (Ansarifar et al. 2019).

Recently, meshless numerical methods are used as alternatives numerical methods like FDM and FEM for solving more complicated problems easily and precisely (Liu and Gu 2005). The meshless techniques are defined as numerical solutions accustomed to set up a system of algebraical equations for the entire domain while not employing a predetermined grid for the model discretization (Liu 2002). Meshfree technique gets rid of the disadvantage of meshing that exists in FDM and FEM (Mohtashami et al. 2017). Using the nodes in meshless solutions for approximation of the governing equations declines the enormous work needed to predetermine for groundwater modeling such as in mesh-based methods (Mohtashami et al. 2022a). Myriad meshless-based strategies found their place in various applications and presented great potential as a remarkable and effective numerical solution tool.

Some of the usage of this methods in groundwater studies are explained.

Li et al. (2003) applied a MFree strategy based on collocation method with radial basis function to model contaminant transport of aquifer . They conducted that the method performed precisely and appropriately. Liu (2006) used radial point collocation method (RPCM) for solving convection–diffusion burger equation in 2D manner based on interpolation scheme. He illustrated that the model performed interestingly for solving fluid-based problems. Mategaonkar and Eldho (2011) applied a MFree model (polynomial point collocation method) to groundwater flow problems in porous media in both 1- and 2-dimensional manner. They illustrated that compared to analytical methods and FEM model, the meshless-based model was more satisfying. Mohtashami et al. (2021) used a meshless method for simulation of groundwater and linked it to particle filter in order to have more precise results.

Although the strategies and methods used to model groundwater systems are very important and each one provides different results, the input data to the models are also of particular importance as the main and initial tools to start the modeling process. As the input data to the model are natural in nature, they may not be uniformly and proportionally distributed in the groundwater system and may be associated with errors. Therefore, the validation and verification of input data to the model significantly influence the accuracy of the model results. Few works have been done to evaluate and validate data using an optimization algorithm. Simulation–optimization models are widely applied for predicting parameters of aquifer based on inverse modeling approach (Swathi and Eldho 2018).

Swathi et al. (2014) applied a MLPG model coupled with partial swarm optimization (PSO) to predict the behavior of groundwater system and optimize the input data simultaneously. Comparing to genetic algorithm (GA) and Levenberg–Marquardt algorithm (LMA), the coupled model represented better results. Thomas et al. (2018) used a simulation–optimization model based on radial point collocation meshfree method (RPCM) coupling with cat swarm optimization (CSO). The results of RPCM-CSO were more satisfying comparing to RPCM-PSO and RPCM-EMPSO (radial point collocation method coupling with elitist mutated partial swarm optimization.

In this study, with aim of finding the precise value of aquifer parameters, a new simulation–optimization named MLPG-MTLBO is engaged. Simulation procedure is carried out with meshless local Petrov–Galerkin (MLPG) and optimization model is modified teaching learning-based optimization (MTLBO), a new developed model in this part. These two models are linked to each other and generate an inverse modeling of MLPG-MTLBO for estimation of aquifer parameters. The proposed model will be applied to two aquifers: A standard and a real one.

Materials and methods

In this section, all the methods used for this study explained including optimization algorithm, simulation model, governing equation, and case studies. In optimization stage, MTLBO in the following of TLBO is going to be described, and then, its procedure for optimizing clearly will be expressed. Then, simulation model, MLPG, will be presented in details.

Modify teaching: learning-based optimization (MTLBO) algorithm

A new version of TLBO algorithm (MTBLO) introduced by Hosseinaei et al. (2021) is used as optimization model in this study. In MTLBO, two terms are added in teaching and learning stages of TLBO algorithm. Exploration and exploitation phases also exist in this model (Hosseinaei et al. 2021).

In the stage of exploration, the entire space is examined and at last the region with the best solutions is found. In the stage of exploitation, the mentioned space of previous stage is examined as well. MTLBO similarly of TLBO has teaching and learning phases. One of the differences is that in teaching stage of MTLBO, a term is added. Also, in learning stage, for increasing the speed of searching some technique is applied. These changes are described in the following paragraph.

In the learning phase, for improving the speed of searching for the best response, movement in search space gets smaller and equals to half of the pervious value. Corrections of the TLBO are considered in two stages.

In the learner phases, despite TLBO, movement is toward the best learning (teaching). In addition of that, to improve the speed of students’ learning, running from the worst learner for more space is applied. Therefore, in MTLBO algorithm, firstly, the students are sorted from the worst to the best (teaching). Based on the noted correction, a new term can be added in teaching stage of the TLBO. The modified teaching stage of the TLBO can be determined in Eq. 1 (Hosseinaei et al. 2021):

$${\text{X}}_{{\text{new,i}}} {\text{ = X}}_{{\text{old,i}}} {\text{ + rand*}}\left( {{\text{X}}_{{{\text{teacher}}}} {\text{ - T}}_{{\text{F}}} {\text{*Mean}}} \right){\text{ + rand*}}\left( {{\text{Mean - X}}_{{{\text{worst}}}} } \right)$$
(1)

In this equation, \({X}_{\mathrm{worst}}\) is the worst grade among all the students and TF denotes to the teaching factor.

In the learning stage, a conceptual analysis of TLBO gets clearer which leads to better solutions. In other words, it is considered that a half of the current dimensions (solutions) are changed in the MTLBO.

Meshless local Petrov–Galerkin (MLPG)

Meshless methods due to its independency of meshing have advantageous in comparison with grid-based methods, e.g., FDM and FEM. However, they are in developing stage, they proved their capability in solving partial differential equations. Many scientists used these methods on their work, regardless to its application, whether fluid or solid and reported their results satisfactory and acceptable (Liu and Gu 2005).

The principle of these methods is to enforce the governed equation on some nodes. Nodes are the element which scattered on boundary and the domain. Distance between nodes can be equal and different. You also have the permission to add or remove nodes whenever you need (Liu 2002).

There are many meshless methods for usage. Application of this method is important as well. For example, some meshless methods must be implemented for fluid problems. SPH (smoothed particle hydrodynamic) is one of the fluid meshless methods that applied to rapid flow like surface water. MLPG is another meshless method that is used in our study.

MLPG is usable in both applications, fluid and solid mechanics. It was proposed on 1998 for the first time by Atluri and Zhu (Atluri and Zhu 1998). They developed this method on some studies in 2000 and 2002 as well. MLPG uses two functions in its main body code, weight and shape function. They are determined by W and \(\varnothing\) in the following equations (Mohtashami et al. 2022b).

Governed equation of groundwater flow in confined aquifer

Groundwater flow equation in transient is expressed in Eq. 2 (Dupouit 1863):

$$k_{x} \frac{\partial }{\partial x}\left( {\frac{\partial H}{{\partial x}}} \right) + k_{y} \frac{\partial }{\partial y}\left( {\frac{\partial H}{{\partial y}}} \right) = S\frac{\partial H}{{\partial t}} + Q \times \delta \left( {x - x_{w} } \right)\left( {y - y_{w} } \right) + q$$
(2)

where \(H\) is groundwater table (m), \(k\) denotes hydraulic conductivity coefficient (m/s), S is specific storage, \(Q\) indicates the rate of extraction or injection flow in wells (– for extraction wells and + for injection wells) [m/s], and q is precipitation with + sign and evaporation with–sign. \(\delta \left(x-{x}_{w}\right)\left(y-{y}_{w}\right)\) is the Dirac delta function.

After discretization of Eq. 2, \(KU=F\) form of equations is generated as Eqs. 3–5:

$$\left[ {\text{K = stiffness}} \right] = k\left( {\left[ {\iint\limits_{\Omega } {\frac{{\partial W_{i} }}{\partial x}\frac{\partial \emptyset }{{\partial x}}d\Omega } + \iint\limits_{\Omega } {\frac{{\partial W_{i} }}{\partial y}\frac{\partial \emptyset }{{\partial y}}d\Omega }} \right]} \right) - \left( {\iint\limits_{\Omega } {W_{i} S\left( {\frac{1}{\Delta t}} \right)d\Omega }} \right)$$
(3)
$$\left[ {U = Unknows} \right] = H^{{\left( {n + 1} \right)}}$$
(4)
$$\left[ {F = {\text{Forcebody}}} \right] = \iint\limits_{\Omega } {W_{i} S\left( {\frac{{H^{\left( n \right)} }}{\Delta t}} \right)d\Omega + Q \times \delta \left( {x - x_{w} } \right)\left( {y - y_{w} } \right)}$$
(5)

\(W\), \(\mathrm{\varnothing }\), \(\Delta t\), \({H}^{(n+1)}\), and \({H}^{(n)}\) are weight function, shape function, time step, groundwater table in the next time step, and groundwater head in the current time step, respectively.

Governed groundwater flow equation in unconfined aquifer

Groundwater flow equation in unsteady state is expressed in Eq. 6 (Wang and Anderson 1995):

$$k_{x} \frac{\partial }{\partial x}\left( {H\frac{\partial H}{{\partial x}}} \right) + k_{y} \frac{\partial }{\partial y}\left( {H\frac{\partial H}{{\partial y}}} \right) = \frac{\partial H}{{\partial t}}S_{y} + Q \times \delta \left( {x - x_{w} } \right)\left( {y - y_{w} } \right) + q$$
(6)

where \({S}_{y}\) is specific yield.

As the following equation substituted in Eq. 6:

$$\frac{{\partial H^{2} }}{\partial x} = 2H\frac{\partial H}{{\partial x}} , \frac{{\partial H^{2} }}{\partial y} = 2H\frac{\partial H}{{\partial y}}$$
(7)

We have:

$$\frac{\partial }{\partial x}\left( {k_{x} \frac{{\partial H^{2} }}{\partial x}} \right) + \frac{\partial }{\partial y}\left( {k_{y} \frac{{\partial H^{2} }}{\partial y}} \right) = 2 \times \left( {\frac{{S_{y} \partial H}}{\partial t} + Q \times \delta \left( {x - x_{w} } \right)\left( {y - y_{w} } \right)} \right)$$
(8)

With considering the assumption that the aquifer is homogeneous and isotropic (\(k_{x} = k_{y}\)):

$$k\left( {\left[ {\left( {\frac{{\partial^{2} H^{2} }}{{\partial x^{2} }}} \right) + \left( {\frac{{\partial^{2} H^{2} }}{{\partial y^{2} }}} \right)} \right]} \right) = 2\left( {S_{y} \frac{\partial H}{{\partial t}} + Q \times \delta \left( {x - x_{w} } \right)\left( {y - y_{w} } \right)} \right)$$
(10)

\(KU = F\) form of linear equations is generated.

$$\left[ K \right] = - 2k\left[ {\iint\limits_{\Omega } {\frac{{\partial W_{i} }}{\partial x}H^{n} \frac{\partial \emptyset }{{\partial x}}d\Omega } + \iint\limits_{\Omega } {\frac{{\partial W_{i} }}{\partial y}H^{n} \frac{\partial \emptyset }{{\partial y}}d\Omega }} \right] - 2\iint\limits_{\Omega } {W_{i} S_{y} \left( {\frac{1}{\Delta t}} \right)d\Omega }.$$
(10)
$$\left[ U \right] = H^{n + 1}$$
(11)
$$\left[ F \right] = - 2\iint\limits_{\Omega } {W_{i} S_{y} \left( {\frac{{H^{n} }}{\Delta t}} \right)d\Omega + Q \times \delta \left( {x - x_{w} } \right)\left( {y - y_{w} } \right)}$$
(12)

Objective function

In this research, the objective function is defined as the weighted difference between observation and simulation groundwater table in that zone gets minimized. In optimization model, the simulated groundwater table is acquired by MLPG flow model. Also, the objective function is the summation of the weighted squared difference of the observation and simulation groundwater values. The objective function is defined as Eq. 13 (Thomas et al. 2018):

$${\text{Min}} S = \mathop \sum \limits_{m = 1}^{M} \mathop \sum \limits_{t = t0}^{{t_{{{\text{final}}}} }} w_{m,t} \left[ {h_{{m,t\_{\text{Obs}}}} - h_{{m,t\_{\text{Com}}}} } \right]^{2}$$
(13)

Subject to upper bound and lower bound on parameters

$${k}_{i,min}\le {k}_{i}\le {k}_{i,max}$$

or

$${Sy}_{i,min}\le {Sy}_{i}\le {Sy}_{i,max}$$

or

$${T}_{i,min}\le {T}_{i}\le {T}_{i,max}$$

In this equation, \({h}_{m,t\_Obs}\) and \({h}_{m,t\_Com}\) are the observation and simulation groundwater tables; \({k}_{i}\), \({Sy}_{i}\), and \({T}_{i}\) are the hydraulic conductivity coefficient, specific yield, and transmissivity coefficients at node i; M is the number of piezometers; \({t}_{0}\) and \({t}_{final}\) are starting and ending time of simulation period, \(S\) is the weighted summation of the squares of the differences between the simulated and observed groundwater table, and \({w}_{m,t}\) is a weighting coefficient.

In this study, the weight coefficient is 1. With using MLPG-MTLBO, the objective function and the parameters are computed. Figure 1 shows the flowchart of our work.

Fig. 1
figure 1

Flowchart of MLPG-MTLBO model

Full size image

The flowchart of the MLPG-MTLBO is drawn in Fig. 1. The model comprises of two simulation and optimization models. MLPG-MTLBO starts from optimization model, the first parameter of optimization algorithm initialized. For computation of objective function, simulation model is started.

Standard aquifer

A confined aquifer, studied in Sharief et al. (2008), is depicted in Fig. 2. Area, thickness, and storage coefficient are 1800*1000 m2, 10 m, and 0.0004, respectively. There are two regions which the aquifer is recharged by them with value of 0.00024 and 0.00012 m/day (Sharief et al. 2008). There are also three extraction wells on the coordinate of (800,200), (800,800), and (1400, 600). The extraction rate from these wells is 200, 500, and 700 m3/day respectively. An injection well is located on (400,800) coordinate and recharges the aquifer with the value of 800 m3/day. The aquifer comprises of three zones. Each zone has different transmissivity coefficient in x and y direction. Boundary conditions for both west and east edges are shown in Fig. 2. North and south sides are impervious as well. Wells located in (600, 400), (1600, 400), and (1000, 600) are determined by observation wells and depicted with blue color.

Fig. 2
figure 2

Representation of 2-dimensional of standard aquifer

Full size image

Real aquifer

Birjand unconfined aquifer which is placed in the east of Iran, South Khorasan province, has 269 km2 area. This aquifer has 190 extraction wells and 10 piezometers. The height of Birjand from the sea is 1491 m. Annual precipitation is 146 mm/year and the average temperature is 16.5 °C. The average thickness of this aquifer is 30 m. Figure 3(a) shows Birjand unconfined aquifer in Iran. In Fig. 3(c), aquifer with its extraction wells (blue symbol) and observation well (red symbols) is determined.

Fig. 3
figure 3

Location of Birjand unconfined aquifer in Iran

Full size image

Results and discussion

In order to investigate the capability of proposed model on finding the aquifer parameters, this model was applied on two aquifers, standard and a real aquifer. Standard aquifer is counted as a real case study with simple geometry, known as a good test case for the MLPG-MTLBO model. As noted previously, this aquifer is divided on three zones with different value of T on each direction (\({T}_{x}\ne {T}_{y}\)).

MLPG-MTLBO with the aim of computing aquifer parameters, i.e., transmissivity coefficients on each zone in this problem, is engaged to this aquifer. In the simulation stage, 60 nodes are scattered on the domain and its boundary. These nodes have the same distance to each other exactly 200 m. Following figure shows the scattered nodes. Blue nodes are placed on the boundary and the red nodes are placed on the domain.

Six ranges of transmissivity coefficient are considered for three zones. Three rages relate to transmissivity coefficient in x direction and three ranges are for transmissivity in y direction. Ranges for \({T}_{x}\) in zone 1, 2, and 3 are [400–600], [300–500], and [200–300], respectively. These ranges for \({T}_{y}\) in zone 1, zone 2, and zone 3 are [200–400], [200–300], and [100–300], respectively.

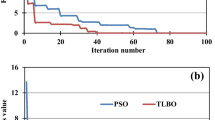
After implementation of the proposed model, transmissivity coefficients are achieved for each zone in each direction. Table 1 shows the computed values against the true values (Fig. 4).

Table 1 Coordinates of observation wells (piezometers) in Birjand aquifer (Majidi et al. 2022)
Full size table
Fig. 4
figure 4

Nodal distribution in standard aquifer

Full size image

According to the table, estimated values by MLPG-MTLBO have a bit higher accuracy than MLPG-TLBO. This is due to the MTLBO optimization which has some modification on its algorithm. The values of relative error of MLPG-MTLBO present the power of MLPG-MTLBO inverse modeling for estimation of aquifer parameter (Table 2).

Table 2 Comparison of MLPG-TLBO and MLPG-MTLBO performance
Full size table

As the revealed results of MLPG-MTLBO are satisfactory for standard case, it is applied in the real case. For the real case, Birjand unconfined aquifer was chosen. Nodes with the equal distance of 500 m are placed on the aquifer and its boundary. Boundary of this aquifer is irregular and has its complexity in simulation stage. Node distribution is depicted in Fig. 5. There are 1175 nodes in this aquifer. A total of 110 of them are on the boundary and determined with blue color. For the purpose of parameters estimation, this aquifer is divided to 14 zones. This makes the cost of computation to be lower. All of the 14 zones are depicted with different symbols and colors in Fig. 5.

Fig. 5
figure 5

Considered 14 different zones in Birjand aquifer

Full size image

For this problem, parameter estimation is carried out for finding hydraulic conductivity coefficients and specific yield. These coefficients are mainly determined by pumping tests, but according to the high cost and complicated condition for these tests, few numbers of them are done for Birjand aquifer. Using MLPG-MTLBO makes it simple and computes the parameters in each zone in a way that the objective function arrives to minimum.

Ranges for hydraulic conductivity coefficient and specific yield are [5–65], [0.01–0.5]. These values are chosen due to the values of pumping test results of for 10 pumping wells located in the aquifer based on the report of regional water company of South Khorasan.

MLPG-MTLBO is applied for this aquifer. Implementation is carried out on a home use laptop (Core I5/8 Gb RAM) and MATLAB 2018 programming software. Results are depicted in Fig. 6.

Fig. 6
figure 6

Achieved results for a) hydraulic conductivity coefficient and b) specific yield

Full size image

Different colors show different values of hydraulic conductivity coefficients and specific yield in the aquifers. Table 3 presents the estimated hydrodynamic values for all the zones of aquifer.

Table 3 Estimated hydrodynamic values for all the zones of aquifer
Full size table

As you can see hydrodynamic parameters for all zones are estimated. Southwest of aquifer has the least value of hydraulic conductivity coefficient around 2 m/day and zone 6 has the maximum value. Maximum and minimum values of specific yield are for zone 8 and zone 13 respectively.

Groundwater table computed with using the estimated parameters achieved by MLPG-MTLBO. Simulation is carried out for a year with monthly time step. Simulation results for the first and the last period of simulation are presented in the following figures and tables. Observation head is also mentioned in these tables (Tables 4 and 5).

Table 4 Groundwater table at the end of first month of simulation
Full size table
Table 5 Groundwater table at the end of last month of simulation
Full size table

According to the results, some error criteria used in groundwater fields, e.g., RMSE, MSE, and ME, are calculated. The formula of these error criteria is explained in Sadeghi Tabas et al. (2017) research.

Table 6 presents the value of error criteria for FDM, MLPG, and MLPG-MTLBO. Based on this table, MLPG-MTLBO has the highest accuracy, Also MLPG is more accurate than FDM. However, all the three numerical methods reveal satisfactory results, but MLPG-MTLBO has the most reliable groundwater head among them.

Table 6 Computation of error criteria for different methods
Full size table

RMSE for MLPG-MTLBO is the least value. This fact shows the accuracy of MLPG-MTLBO in estimation of aquifer parameters that leads to results with this accuracy. Following figures indicate computed groundwater head for all twelve months in each piezometer based on the applied numerical method.

These graphs show the results of three different methods in comparison with observation groundwater. Observation graph (orange line) presents the groundwater head where all the results must be compared to it. The blue line indicates MODFLOW head which is based on FDM. All the blue lines have the same trend with observation line. This fact shows the power of FDM in modeling. However, blue lines have distance to observation line in comparison with other lines.

Red line stands for MLPG results which is derived by Mohtashami et al. (2017) research. As it can be seen, MLPG is more accurate than FDM. Trend of MLPG generally does not follow the trend of observation line. For instance, in piezometer 7, MLPG has increasing trend; however, observation line is decreasing. Totally, MLPG is closer than FDM to observation results. It is noticeable that in piezometer 4 in the sixth month due to the high extraction of groundwater in the location of that piezometer, a huge drawdown occurred on the aquifer based on MLPG.

Our proposed model (black line), MLPG-MTLBO, is depicted in Fig. 7. MLPG-MTLBO has the exact trend of observation results. Also, the acquired results by MLPG-MTLBO have the most closeness to observation values. This means the good performance of MLPG-MTLBO model in estimating aquifer parameters leads to high accuracy of groundwater head.

Fig. 7
figure 7

Comparison of different models in simulation stage

Full size image

According to the computed groundwater tables for all nodes, 3-dimentional view of aquifer is illustrated in Fig. 8. Groundwater table is higher in the east of aquifer, and it has decreasing value while traveling to the west. At the center of aquifer, as it obvious, due to the dense of extraction wells, drawdown is appeared.

Fig. 8
figure 8

Acquired groundwater head after one year simulation in a) 3D view b) 2D view

Full size image

West of the aquifer has the least groundwater head around 1264.45 m.

Conclusion

Understanding the behavior of groundwater system is highly dependent on precise value of aquifer parameters. In order to estimate these parameters, an inverse modeling would be suggested and applied. This study uses simulation–optimization model as an inverse modeling for this purpose. MLPG-MTLBO is S/O model that for parameter estimation, minimized, the summation of the weighted squared difference of the observation and simulation groundwater values. In the most minimization state, aquifer parameters will be derived. MLPG-MTLBO is applied on two aquifers, standard and a real case study. On standard aquifer, transmissivity coefficients for three different zones are computed. The closeness of estimated values to true ones shows the power of this S/O model. Big challenge for this model is the real aquifer. MLPG-MTLBO is engaged on Birjand unconfined aquifer. Hydraulic conductivity coefficients and specific yield are computed for 14 zones of Birjand aquifer. The estimation is too precise that makes the RMSE to reduce from 0.757 to 0.356 m. This means the power of engaged S/O model for this purpose.