Introduction

Evaporation is defined as a physical process where the water molecules escaped from the surface as enough energy is absorbed that overcomes the vapor pressure (Malik et al. 2021). Evaporation hence constitutes the majority of losses that might be occurred in any water system which could be thence exacerbated water scarcity. This is exceptionally true in arid to semi-arid areas where the molecules have enough heat energy to escape. Therefore, an accurate estimation of the evaporation losses play a pivotal role in better water resources management, crop water demands and irrigation scheduling (Fan et al. 2016; Gong et al. 2021; Kushwaha et al. 2021).

In arid and semi-arid regions, high rates of evaporation are typically be witnessed in the summer season. Thence, water losses into the atmosphere from reservoirs, river basins, and natural lakes might be exacerbated leading to deterioration of water levels (Boers et al. 1986; Sayl et al. 2016; Khan et al. 2019). As such, an accurate quantification of losses from water bodies is crucially important to be considered for proper planning and managing of any water resources project (Abd-Elaty et al. 2022; Moazenzadeh et al. 2018; Vishwakarma et al. 2022). Recently, the impact of climate changes has exacerbated the influence of evaporation on surface water balance (Sartori 2000), where the global warming has negative influence on the relationship between evaporation and water management (Eames et al. 1997; Kushwaha et al. 2016, b).

There are two ways to estimate evaporation; either directly such as the pan evaporation (PE) method or indirectly like mass transfer, water and energy balance (Lundberg, 1993), and Penman methods (Zhao et al. 2013). However, the Class A pan method is globally used for estimating evaporation as it is well adapted to relatively estimate the evaporation levels in different climatic characteristics regions (Masoner et al. 2008). Accordingly, the evaporation amount of 60- or 20-cm-diameter pans can be converted into that amount of Class A pan. Nonetheless, the costly nature of the class A method represents the essential obstacle of its application in many developing countries (Ashrafzadeh et al. 2019; Wu et al. 2020). In order to be reliably predictive, the evaporation losses models should be accounting for the driving meteorological variables such as relative humidity (RH), sunshine hours (Sh), wind speed (WS), rainfall (RF), minimum (Tmin), maximum (Tmax), and mean (Tmean) temperatures. As such, many of empirical models have been configured for predicting evaporation rates from metrological variables like Thornthwaite equations, Priestley–Taylor and Penman–Monteith. However, the stochasticity features in addition to the nonlinearity and non-stationary of the meteorological variables employed in building a predictive model necessitate developing rigorous and reliable intelligent models that could be capable to eliminate the stochasticity inherited in the evaporation-meteorological variables relationship (Elbeltagi et al. 2022; Kisi et al. 2017a; Kushwaha et al. 2022a; Salih et al. 2020; Khan et al. 2018; Naganna et al. 2019).

Owing to its capacity in tackling the complexity accompanied by highly stochastic features of many environmental problems (Chia et al. 2020), machine learning (ML) methods have been recently identified as a paramount method to address various aspects of the association between predictors and predictands. In the literature, many successful applications of machine learning methods were reported in various topics of hydrology and climatology. For instance, rainfall (Salih et al. 2020; Adnan et al. 2021), streamflow (Parisouj et al. 2020; Feng and Tian 2020), drought (Malik et al. 2020a; Parisouj et al. 2020), surface water quality (Rezaie-Balf et al. 2020; Chen et al. 2020), groundwater (Mosavi et al. 2021; Rahman et al. 2020), evapotranspiration (Granata 2019; Ferreira and da Cunha 2020; Granata et al. 2020; Granata and Di Nunno 2021), and many others (Al-Mukhtar 2019; Ghaemi et al. 2019; Keshtegar et al. 2019; Majhi et al. 2020; Yang et al. 2020). As a case in point, the applicability of deep neural network architecture with long short-term memory (Deep-LSTM) cells to estimate daily pan evaporation with minimum input features was investigated in a study by Majhi et al. (2020). They proposed to that end number of input combinations to predict the daily evaporation rates in three areas of Chhattisgarh state in India. The investigation suggested that the proposed Deep-LSTM model was capable to successfully model the daily evaporation losses with improved accuracy as compared to multilayer artificial neural network and empirical methods (Hargreaves and Blaney–Criddle). In another study by Zhu et al. (2020), the performance of hybridized extreme learning machine (ELM) model with particle swarm optimization (PSO) was explored to estimate the daily ETo in the arid region of Northwest China. The comparison of the obtained results with those counterparts from the original ELM, artificial neural networks (ANN) and random forests (RF) models along with six empirical models indicated a superior performance of ELM-PSO models for estimating ETo more accurately than others. A comparative study on the performance of ElasticNet linear regression, extreme gradient boosting, long short‑term memory in addition to two empirical techniques, i.e., Stephens‑Stewart and Thornthwaite, was carried out by Abed et al. (2021) in two weather stations in Malaysia. They found that the ML models outperformed the empirical models with the same input configurations. The bat algorithm (Bat) was coupled with gradient boosting in a study by Dong et al. (2021). Its performance was compared with random forest and original CatBoost (CB) for forecasting daily pan evaporation in arid and semi-arid regions of northwest China. They pointed out that the hybrid model outperformed the other models and presented comprehensive performance results (seasonally and spatially) compared to CatBoost and random forest. Emadi et al. (2021) evaluated the applications of wavelet-hybrids artificial neural networks (WANN), adaptive neuro-fuzzy inference system (WANFIS), and gene expression programming (WGEP) to estimate monthly evaporation in a study area in the Northwest and central part of Iran. They compared their results with those standalone models. It was revealed that the WGEP method has superiority in terms of performance and accuracy in comparison with the others and single models.

From the above-mentioned literature, it has been demonstrated that the ML performances were superior in comparison with other methods and depending on the input factors under various climatic conditions, the performance varies. However, the hybrid technique, where two or more models are combined and coupled (Chia et al. 2020), has recently drew more attention in climate and hydrology studies because of its capacity to capture the various patterns in data series by combining multi-technique features in one algorithm (Ghaemi et al. 2019). Yet, the generalization of the capability of these models over various climatic zones is arguable (Al-Mukhtar 2019) owing to the fact that each climatic region is associated with certain characteristics of stochasticity and non-stationarity. Therefore, it is essential to investigate newly developed models and explore their applicability for specific climatic features. As such, the main aim of this study was to explore the predictability of new hybrid methods, i.e., bagging and random subspace-based reduced-error pruning tree (REPTree) algorithms for modeling pan evaporation rates. Using these methods in water-related subjects has been rarely reported in the literature. Therefore, this study represents a novel framework to increase the prediction accuracy of applying machine learning in solving such complex physical relationships.

Materials and methods

Study area and data

The study area encompasses three different areas in Iraq which are Baghdad, Basrah, and Mosul. The latitude–longitude–altitude of the above stations are 33° 20′ 26″ N- 44° 24′ 03″ E- 41 m a.s.l, 30° 31′ 58″ N- 47° 47′ 50″ E- 6 m a.s.l, and 36° 20′ 06″ N- 43° 07′ 08″ E- 228 m a.s.l, respectively. These areas are situated in the middle, south, and north of Iraq, respectively (Fig. 1). Accordingly, the meteorological parameters which include T max., T min., T mean, WS, and RH to predict the monthly pan evaporation were collected for the study areas. The collected data span over the period of 1990–2013 for Baghdad and Mosul stations and 1990–2012 for Basrah, on a monthly time scale. The collected data were subdivided into two datasets, i.e., 75% for training and 25% for testing. The detailed statistical characteristics of the climatic parameters used in modeling configurations are listed in Table 1. The climatic condition at the selected stations is represented by climate variables (Table 1) such as Tmin (0.7–32.9 °C), Tmax (12.9–47.70 °C), RH (20–82%), WS (1.4–2.5), and PE (48.70–624.80 mm) at Baghdad; Tmin (4.7–34.60 °C), Tmax (14.60–48.90 °C), RH (17–80%), WS (1.7–7.7 m/s), and PE (41.40–645.90 mm) at Basrah; and Tmin (− 2.2–27.40 °C), Tmax (8.30–46.40 °C), RH (19–88%), WS (0.2–3.7 m/s), and PE (21.50–464.10 mm) at Mosul station, respectively.

Fig. 1
figure 1

The study area location

Full size image
Table 1 Statistics of the measured meteorological parameters at study areas
Full size table

Methods

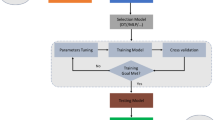
Five evolutionary ML methods were evaluated in this study for forecasting PE, which are additive regression (AR), additive regression-random subspace (AR-RSS), AR-Bagging, additive regression-reduced error pruning tree (AR-REPTree), and AR-M5 pruned models. The evaluated methods were applied on data from three different climatic stations in Iraq. The proposed methodology applied in this study was explained as given in Fig. 2. A brief description on the individual methods is given in the following.

Fig. 2
figure 2

The flowchart of the proposed methodology

Full size image

Additive regression AR

AR is a nonparametric regression method suggested by Friedman and Stuetzle (1981). In contrast to the ordinary regression, AR uses one smoother function to describe the relationship between predictors and predictands. As such, it can overcome the issue of curse dimensionality inherited in other p-dimensional smoother. The additive model takes the following form:

$$ E\left[ {y_{i} |x_{i1} , \ldots , x_{ip} } \right] = \beta_{o} + \sum\nolimits_{j = 1}^{p} {f_{i} \left( {x_{ij} } \right)} $$
(1)

where \(\sum\nolimits_{j = 1}^{p} {f_{i} \left( {x_{ij} } \right)}\) are the smooth functions fitted from the data and \(\beta_{o}\) is the regression coefficient.

Random subspace (RSS)

RSS is one of the machine learning ensemble methods which is used for decision trees. In contrast to other trees-based decision methods, the method uses a systematic construction of decision trees in which each tree is being independently generated based on parallel learning algorithm (Ho 1998). Additionally, its structure as an ensemble learning method works on reducing the correlation between learners by randomly sampling subset of the training points and features instead of the entire both dataset. Thence, the learners produce different models that can be reliably averaged. The generated trees are clustered randomly into subspaces through a majority voting method. So that, the majority of voting is employed in the subspace ensemble system for the sample of X (Eq. (2)):

$$ \beta \left( x \right) = \arg \max_{{y \in \left( { - 1,1} \right)}} \sum\nolimits_{b} {\delta_{{{\text{sgn}} \left( {C^{b} \left( x \right)} \right),y}} } $$
(2)

where \(\delta\) is the Kronecker symbol and y ∈ {− 1, 1} is a decision (class label) of the classifier, \(C^{b} \left( x \right)\) is the classifier of each subspace b (Skurichina and Duin 2002).

One of the attractive features of RSS is being sensibly adapted for high-dimensional problems where the number of features is much larger than the number of training points (Arabameri et al. 2021).

M5 pruned (M5P)

M5 model tree method (Quinlan 1992) is a tree-based model used in solving predictor-predict and regression problems of numerical values (Kisi et al. 2017b). In this method, two main steps are adopted in building the M5 model, i.e., data splitting into subsets at each node; and constructing a multivariate regression for each node (Malik et al. 2020a). In the first step, the data are split by computing the standard deviation reduction (SDR) at each leaf (Eq. (3)). So that the standard deviation of the classes values reaching a node is treated as an error index at that node. Subsequently, the expected reduction of that error is calculated by testing each attribute at that node. Thence, the subsets data are selected based on maximizing the expected error reduction (Al-Mukhtar 2021a).

$$ {\text{SDR}} = sd\left( T \right) - \sum\nolimits_{i} {\frac{{\left| {T_{i} } \right|}}{\left| T \right|} \times sd(T_{i} )} $$
(3)

where T is a set of cases in the data that reach a node, \(sd\) is the standard deviation, and \(T_{i}\) is the subset of cases that have the ith outcomes of the potential test.

In the second step, a multivariate linear regression model is constructed for each node at the model subtree. The M5 model compares the accuracy of the constructed linear model with the subtree at this node to ensure the same level of information. The decision on selection the optimal model is concluded based on the lower estimated error from either the obtained linear model or the model subtree. To minimize the standard error, the linear models are simplified by eliminating parameters using a greedy search method to remove variables which have little contribution to the model. Finally, the pruning and smoothing processes are set up to improve the prediction accuracy (Arabameri et al. 2021). The non-leaf nodes starting from the tree bottom are examined so that the subtree at a node is pruned depending on the least estimated error. If the linear model is opted, the subtree at this node is pruned as a leaf. The prediction accuracy is ultimately enhanced by the smoothing process where the predicted value at the leaf is adjusted by the equation below:

$$ PV\left( S \right) = \frac{{n_{i} \times PV\left( {S_{i} } \right) + k \times M\left( S \right)}}{{n_{i} + k}} $$
(4)

where \(PV\left( {S_{i} } \right)\) is the predicted value at \(S_{i}\), \(n_{i}\) number of training cases, \(S_{i}\) is the case follow a branch of subtree \(S\), \(k\) is the smoothing factor, and \(M\left( S \right)\) is the value given by the model at \(S\).

Reduced error pruning tree (REPTree)

REPTree is one of the pruning algorithms used in machine learning that characterize as simple and computationally speed (Quinlan 1987). It has been commonly used as a baseline method for the purpose of comparison with other pruning methods (Mohamed et al. 2012; Ganatra and Bhensdadia 2012). The algorithm is based on the principle of information gain and reducing the variance error (Chen et al. 2019a, b). The data are split based on the information gain reach at each node, and then, the subtrees are pruned by the reduced error. The algorithm starts from every non-leaf subtree in the test data where the change in misclassification is examined which arises when the subtree is replaced by the most common classified class at the node (Quinlan 1987). The subtree would be replaced by a leaf when the new induced tree has equal or less error than before. The process is repeated over until any further replacements increase the variance error of the test data.

Bagging

Bagging or bootstrap aggregating (Breiman 1996) is the most common ensemble learning method which is used to improve the accuracy performance of forecasting models (Li et al. 2020) by reducing the variation of a noisy data. In bagging, multiple learning algorithms are combined to obtain better predictive performance so that a stronger learners are constructed from weak ones (Saha et al. 2016). In contrast to other ensemble learning, a bootstrap replication of the original dataset is used to generate training sets and trains the base learners on these sub datasets (Al-Mukhtar 2021b). Then, the bagging averages out the resulting models in regression problems (Tyralis et al. 2019).

Statistical performance indicators

Five statistical performance indicators, i.e., mean absolute error, root mean square error, relative absolute error, root relative standard error, the correlation coefficient were applied to assess the five predictor AI models. The mathematical expression of each indicator is explained as below (Moriasi et al. 2007):

Mean absolute error (MAE)

$$ {\text{MAE}} = \frac{1}{N}\sum\nolimits_{1}^{N} {\left| {PE_{p}^{i} - PE_{O}^{i} } \right|} $$
(5)

Root mean square error (RMSE)

$$ {\text{RMSE}} = \sqrt[2]{{\frac{1}{N}\sum\nolimits_{i}^{N} {\left( {PE_{O}^{i} - PE_{p}^{i} } \right)^{2} } }} $$
(6)

Relative absolute error (RAE)

$$ {\text{RAE}} = \left| {\frac{{PE_{O}^{i} - PE_{p}^{i} }}{{PE_{p}^{i} }}} \right| \times 100 $$
(7)

Root relative square error (RRSE)

$$ {\text{RRSE}} = \frac{{\sqrt[2]{{\mathop \sum \nolimits_{I}^{N} \left( {PE_{p }^{i} - PE_{O }^{i} } \right)^{2} }}}}{{\sqrt[2]{{\mathop \sum \nolimits_{I}^{N} \left( {PE_{O }^{i} - \overline{{PE_{O} }} } \right)^{2} }}}} $$
(8)

The correlation coefficient (r)

$$ r = \frac{{\mathop \sum \nolimits_{i}^{N} (PE_{O }^{i} - \overline{{PE_{O} }} )\left( {PE_{p }^{i} - \overline{{PE_{p} }} } \right)}}{{\sqrt[2]{{\mathop \sum \nolimits_{I}^{N} \left( {PE_{O }^{i} - \overline{{PE_{O} }} } \right)^{2} \mathop \sum \nolimits_{I}^{N} \left( {PE_{p }^{i} - \overline{{PE_{p} }} } \right)^{2} }}}} $$
(9)

where N is the total number of data points, \(PE_{O}^{i}\) is the observed evaporation value, \(PE_{p}^{i}\) is the predicted evaporation value, and \(\overline{{PE_{O} }} \) and \(\overline{{PE_{p} }}\) are the mean values of the observed and predicted evaporation values, respectively.

Results

The forecast results for the best data-driven models for each station (Baghdad and Mosul) are shown in the sections below. The projections offered are based on validation data sets for time series of evaporation, which is often used to characterize agricultural meteorological events such as droughts and for irrigation system design. The applied models were set up using data from three different climatic characteristics stations in Iraq. The parameters of the machine learning algorithm used for modeling PE in these three regions were listed as shown in Table 2.

Table 2 The tuning parameters of the applied models
Full size table

Input selection using best subset model

The selection of the optimal input parameters is a critical step in modeling for the best performance of the chosen models. For the optimal input combination, many combinations of meteorological parameters were used. Tables 3, 4 provide the statistical analysis of the five combinations that were examined in this research. At two stations in Baghdad and Mosul, the optimal input combination was chosen using the seven statistical criteria of MSE, R2, adjusted R2, Mallows' Cp, Akaike's AIC, Schwarz's SBC, Amemiya's PC, with the results presented in Tables 3, 4. The smallest and nearest to zero values of MSE, Mallows' Cp, Akaike's AIC, Schwarz's SBC, Amemiya's PC and the highest and near to 1 values of R2, adjusted R2 considered as best input combination in subset linear regression analysis.

Table 3 Inputs selection using regression analysis for modeling PE at Baghdad station
Full size table
Table 4 Inputs selection using regression analysis for modeling PE at Mosul station
Full size table

The bold blue row in Table 3 is observed as the optimum input combination because it contains the lowest values of MSE of 1733.377, Mallows' Cp of 4.229, Akaike's AIC of 2151.826, Schwarz's SBC of 2166.478 and Amemiya's PC of 0.103, and the highest values of R2 (0.934) and Adj-R2 (0.934) of all input combinations at the Baghdad station. A similar result is seen in Table 4, where the bold blue row was observed as the optimum input combination, with the lowest values of MSE of 979.668, Mallows' Cp of 5.00, Akaike's AIC of 1988.474, Schwarz's SBC of 2006.789 and Amemiya's PC of 0.061, and the highest values of R2 (0.940) and Adj- R2 (0.939) among all the input combinations at the Mosul station.

Sensitivity analysis

The inputs combinations predominantly influence the performance of the models. Some may provide a positive contribution to the accuracy of the chosen model, while others might make a negative contribution. The selection of the most important relevant factors was carried out using sensitivity analysis to capture the optimal performance of daily PE models at two stations in Iraq. Tables 5, 6, as well as Figs. 3, 4 show the findings of the regression analysis that was conducted. The results of the regression analysis on all input parameters revealed that Tmax, Tmin, Tmean, RH, and WS, with absolute standard error coefficients of 0.000, 0.000, 0.038, 0.039, and 0.018, were identified as the most influential input parameters for estimation of evaporation at the Baghdad, whereas, absolute standard error coefficients were 0.000, 0.172, 0.213, 0.061, and 0.015 at Mosul station, respectively. The standardized coefficients of the input variable for sensitivity analysis are shown in Figs. 3, 4 for Baghdad and Mosul station, respectively.

Table 5 Sensitivity analysis of input variables at Baghdad station
Full size table
Table 6 Sensitivity analysis of input variables at Mosul station
Full size table
Fig. 3
figure 3

The standardized coefficients of input variable for sensitivity analysis at Baghdad station for evaporation

Full size image
Fig. 4
figure 4

The standardized coefficients of input variable for sensitivity analysis at Mosul station for evaporation

Full size image

Modeling of pan evaporation

In the present study, five evolutionary machine learning, additive regression, AR-RSS, AR-Bagging, AR-REPTree, and AR-M5P models, were applied for forecasting monthly evaporation, and results were compared with classic AR to see the accuracy improvement of the new methods. For this purpose, the MAE, RMSE, RAE, RRSE, and r measures were considered.

Training and testing the selected models at Baghdad station

The monthly PE was estimated using AR, AR-RSS, AR-Bagging, AR-REPTree, and AR-M5P models based on MAE, RMSE, RAE, RRSE, and r for both training and testing stages at Baghdad station. The values of MAE, RMSE, RAE, RRSE, and r criteria during the training and testing periods for AR, AR-RSS, AR-Bagging, AR-REPTree, and AR-M5P models are presented in Table 7. As evaluated for Baghdad station from Table 7, the AR, AR-RSS, AR-Bagging, AR-REPTree, and AR-M5P models provided MAE = 30.34, 31.12, 31.33, 33.313, and 29.65; RMSE = 41.19, 41.50, 40.14, 44.35, and 39.58; RAE = 21.18, 21.73, 21.87, 23.25, and 20.70; RRSE = 25.27, 25.47, 24.63, 27.21, and 24.29; r = 0.968, 0.967, 0.970, 0.962, and 0.970 during training period. In addition, the AR, AR-RSS, AR-Bagging, AR-REPTree, and AR-M5P models provided MAE = 35.51, 45.72, 37.74, 37.81, and 33.82; RMSE = 48.68, 59.18, 47.35, 50.13, and 45.05; RAE = 25.98, 33.46, 27.62, 27.67, and 24.75; RRSE = 30.80, 37.44, 29.96, 31.72, and 28.50; r = 0.966, 0.949, 0.962, 0.958, and 0.972 during testing period, respectively. Table 7 showing the AR-M5P model attained the most accurate simulation during the testing stage. Therefore, AR-M5P model was the best performed model according to the statistical criteria (i.e., minimum MAE, RMSE, RAE, and RRSE values, and maximum r values) in testing stage followed by AR-Bagging model closely.

Table 7 MAE, RMSE, RAE, RRSE, and r for meta-heuristics algorithms-based models during the training and testing span at Baghdad station
Full size table

The temporal variation along with the scatter plots (right side) of the simulated versus observed monthly evaporation data for the AR, AR-RSS, AR-Bagging, AR-REPTree, and AR-M5P models is plotted in Fig. 5a–e during the testing stage. In scatter plots, the regression line provided the coefficient of determination (R2) as 0.934 for the additive regression (AR) model, 0.902 for the AR-RSS model, 0.925 for AR-Bagging model, 0.918 for AR-REPTree model, and 0.944 for AR-M5P model during the testing stage, respectively. The regression line (RL) and the line of 1:1 were close to each other for all models. The RL was above the best fit (1:1) for AR, AR-RSS, AR-Bagging, AR-REPTree, and AR-M5P models. This means that at Baghdad station, the five models slightly overpredict the monthly PE values. Radar charts display MAE and RSME of AR, AR-RSS, AR-Bagging, AR-REPTree, and AR-M5P models during testing at Baghdad station plotted in Fig. 6. As can be raised from Fig. 6, the applied models were very close to each other. In other words, AR-REPTree was seen as the furthest from the observed point which introduces the AR-REPTree model as the worst model. On the opposite side, AR-M5P was the closest model to the observed point based on the standard deviation, correlation, and RMSE (Fig. 7). This demonstrates the superiority of the AR-M5P model in comparison with the others.

Fig. 5
figure 5figure 5

Observed vs estimated daily evaporation values by the AR, AR-RSS, AR-Bagging, AR-REPTree, and AR-M5P models during testing at Baghdad station

Full size image
Fig. 6
figure 6

Radar charts display MAE and RSME of AR, AR-RSS, AR-Bagging, AR-REPTree, and AR-M5P models during testing at Baghdad station

Full size image
Fig. 7
figure 7

Taylor diagrams of AR, AR-RSS, AR-Bagging, AR-REPTree, and AR-M5P during testing span at Baghdad station

Full size image

Training and testing the selected models at Mosul station

The monthly PE was estimated using AR, AR-RSS, AR-Bagging, AR-REPTree, and AR-M5P models based on MAE, RMSE, RAE, RRSE, and r for both training and testing stages at Mosul station. The values of MAE, RMSE, RAE, RRSE, and r criteria during the training and testing periods for AR, AR-RSS, AR-Bagging, AR-REPTree, and AR-M5P models are given in Table 8. As evaluated for Mosul station from Table 8, the AR, AR-RSS, AR-Bagging, AR-REPTree, and AR-M5P models provided MAE = 23.62, 21.97, 22.46, 26.66, and 22.75; RMSE = 33.96, 29.38, 29.97, 38.09, and 29.21; RAE = 20.42, 19.00, 19.42, 23.05, and 19.67; RRSE = 26.24, 22.71, 23.16, 29.43, and 22.57; r = 0.965, 0.974, 0.972, 0.957, and 0.974 during training period. In addition, the AR, AR-RSS, AR-Bagging, AR-REPTree, and AR-M5P models provided MAE = 29.68, 26.93, 27.37, 27.01, and 25.82; RMSE = 42.34, 37.31, 37.94, 38.62, and 35.95; RAE = 27.30, 24.77, 25.17, 24.84, and 23.75; RRSE = 34.92, 30.77, 31.29, 31.85, and 29.64; r = 0.945, 0.959, 0.959, 0.962, and 0.956 during testing period, respectively. Table 8 proves that the AR-M5P model outperformed the other models during the testing period according to the statistical criteria (i.e., minimum MAE, RMSE, RAE, and RRSE values, and maximum r values) in testing stage followed by AR-RSS model.

Table 8 MAE RMSE, RAE, RRSE, and r for meta-heuristics algorithms-based models during the training and testing span at Mosul station
Full size table

The temporal variation along with the scatter plots (right side) of the simulated versus observed monthly evaporation data for the AR, AR-RSS, AR-Bagging, AR-REPTree, and AR-M5P models is plotted in Fig. 8a–e during the testing stage. The coefficient of determination (R2) was 0.894 for the AR model, 0.921 for the AR-RSS model, 0.921 for AR-Bagging model, 0.926 for AR-REPTree model, and 0.915 for AR-M5P model during the testing stage, respectively. It can be revealed that the RL and the line of fit (1:1) were close to each other for all applied models. The RL was above the best fit (1:1) for AR, AR-RSS, AR-Bagging, AR-REPTree, and AR-M5P models which implies that at Mosul station, the five models slightly overpredict the monthly PE values. Radar charts display MAE and RSME of AR, AR-RSS, AR-Bagging, AR-REPTree, and AR-M5P models during testing at Mosul station plotted in Fig. 9. It is noticed that all models were very close to each other; however, AR was the furthest from the observed point, while AR-M5P was the closest. Suggesting that AR-REPTree was the worst model, and AR-M5P was the best based on the standard deviation, correlation, and RMSE (Fig. 10).

Fig. 8
figure 8figure 8

Observed vs estimated daily evaporation values by the AR, AR-RSS, AR-Bagging, AR-REPTree, and AR-M5P models during testing at Mosul station

Full size image
Fig. 9
figure 9

Radar charts display the best performance indicators of AR, AR-RSS, AR-Bagging, AR-REPTree, and AR-M5P models during testing at Mosul station

Full size image
Fig. 10
figure 10

Taylor diagrams of AR, AR-RSS, AR-Bagging, AR-REPTree, and AR-M5P during testing span at Mosul station

Full size image

Validation best candidate model at Basrah station

The best selected model was utilized for validation to predict of monthly evaporation at Basrah station. AR-M5P model was found best algorithm for both stations, i.e., Baghdad and Mosul; therefore, AR-M5P model was used for validation of best candidate model at Basrah station. The values of MAE, RMSE, RAE, RRSE, and r criteria during the validation period AR-M5P models are presented in Table 9. As evaluated for Basrah station from Table 9, the AR-M5P models provided MAE, RMSE, RAE, RRSE, and r = 47.23, 67.23, 31.19, 39.30, and 0.942, respectively.

Table 9 Validation results (i.e., MAE, RMSE, RAE, RRSE, and r) for best candidate model at Basrah station
Full size table

The temporal variation along with the scatter plots (right side) of the simulated versus observed monthly evaporation data for the AR, AR-RSS, AR-Bagging, AR-REPTree, and AR-M5P models is plotted in Fig. 11 during the testing stage. In scatter figure, the coefficient of determination (R2) was 0.887. The fitted RL and the perfect line of fit (1:1) were close to each other. The RL was above the best fit (1:1) for AR-M5P models. This means that at Basrah station, the model slightly overpredicts the monthly PE values.

Fig. 11
figure 11

Observed vs estimated daily evaporation values by the best model AR-M5P during validation at Basrah station: a temporal variation; b scatter plot

Full size image

Discussion

According to the results of the subset regression analysis, the best input combination for the Baghdad station was selected as T, RH, and W, and the best input combination for the Mosul station was selected as Tmin, T, RH, and W, indicating that all of these variables have an effect on pan evaporation. According to the relevant literature, all of these factors have a physical impact on pan evaporation. This demonstrates that the subset regression analysis was performed correctly. The heuristic models AR-M5P outperform the other algorithm models at both stations when compared to the other algorithms. As a result, the AR-M5P model was employed for the validation of the best candidate model at the Basrah station. The use of all of these models in various contexts may only be conceivable after they have been calibrated with fresh data. It was discovered that all of the heuristic models significantly overestimated the pan evaporation values, particularly for the Baghdad, Mosul, and Basrah stations, with the exception of one. One possible explanation for this might be the disparity between the training, test, and validation data ranges at this station. As a result, extrapolating the results of the applicable models becomes challenging.

The results of this study were validated with other recent works (Chen et al. 2019a, b; Kumar et al. 2021; Kushwaha et al. 2021; Lin et al. 2013; Malik et al. 2020b; Vishwakarma et al. 2022) conducted in different continents of the world. Lin et al. (2013) investigated the performance of two different ML techniques (i.e., SVM and backpropagation network) for estimating daily evaporation values. They demonstrated the superiority of the applied support vector machine to estimate the daily PE values and revealed that it can be used as promising alternative for evaporation prediction. The predictability of five ML methods [i.e., multi-model artificial neural network (MM-ANN), MARS, SVM, multi-gene genetic programming (MGGP), and M5Tree] to predict the monthly PE in India was investigated by Malik et al. (2020a), who made a similar commitment. They reported that the MM-ANN and MGGP algorithms were superior in prediction performance when compared to the MARS and SVM algorithms, as well as the M5Tree method as indicated by lowest RMSE. Kushwaha et al. (2021) evaluated four ML algorithms (i.e., SVM, RT, REPTree, and RSS) under diverse climate conditions in Northern India. They concluded that SVM outperformed over other applied algorithms as it has a high value of correlation coefficient and Willmott index and low value of MAE and RMSE. Similarly, Chen et al. (2019a, b) evaluated the prediction of monthly PE from SVM at 6 different stations, located in the Yangtze River in China. They proved that SVM was better than the traditional methods for estimating PE. In parallel to the above literature, the findings of this study confirmed that the AR-M5P hybrid algorithm was more accurate than other applied algorithms in terms of predicting the pan evaporation rates at the selected stations.

Overall, our findings indicate that hybrid models have a stronger predictive value in real-world situations and maybe employed more effectively in watersheds with little data. In addition to predicting pan evaporation, these types of models may be used to forecast a wide range of hydrological and water resources phenomena, including ETo, suspended and bed sediment loads, rainfall, and groundwater contamination. Especially in developing countries where technical skills and understanding of the processes occurring in the watershed are lacking, these algorithms could be used in data-poor watersheds or for measuring some phenomena that are time-consuming or expensive, such as suspended or bed load in rivers, or nitrate and other heavy metals measurement in groundwater. Lastly, it is noteworthy to mention that despite the superior performances of hybrid meta-heuristics algorithms proved through the present study; several drawbacks and limitations might be diagnosed which hinder a generalized conclusion. Such as limitations are represented by the uncertainties inherited in inputs datasets, the established scenarios, modeling methods with large search space and model parameters, etc. where all the above mentioned conditions are ultimately influence the applicability of the proposed methods. Hence, further validations should be carried out to validate the methods at different areas under different agroclimatic conditions with various scenarios.

Conclusions and outlook

In this study, five machines learning evolutionary were applied for forecasting monthly evaporation and results were compared with classic AR to see the accuracy improvement of the new methods. The developed models encompass additive regression, AR-RSS, AR-Bagging, AR-REPTree, and AR-M5P models. Data from three different climatic characteristics regions in Iraq were employed for the sake of models evaluations using several statistical metrics (MAE, RMSE, RAE, RRSE, and r). The best input combination was determined based on the regression subset. As such, the optimal input combination for the Baghdad station was Tmean, RH, and WS, and the best input combination for the Mosul station was Tmin, RH, and WS, indicating that all of these variables affect pan evaporation. It was concluded that the hybrid models have a stronger predictive capability in real-world situations and maybe employed more effectively in watersheds with little data. However, the AR-M5P was found to be the best performance among the other evaluated methods as it shows the least error indices values. The statistical indicators, i.e., the MAE, RMSE, RAE, RRSE, and r, obtained from AR-M5P in Baghdad were 33.82, 45.05, 24.75, 28.50, and 0.972, respectively, while those indicators in Mosul were 25.82, 35.95, 23.75, 29.64, and 0.956, respectively. The superior performance from AR-M5P highlighted the effectiveness of using AI methods in tackling complicated relationships which could be used for further data analysis in water resources and hydrology.