Introduction

Water contamination is one type of pollution caused by improper use of pesticides. It simply refers to the presence of undesirable substances in water, altering its properties and rendering it unfit for use. This can occur when pesticides are applied to croplands and are carried away by wind and rainfall into water bodies (Abdelhameed et al. 2018; Rani and Shanker 2018). As a result, they alter the physical, chemical, and biological conditions of such water bodies, rendering them toxic and contaminated (Bayat et al. 2018; Arihilam and Arihilam 2019; Gomes et al. 2018). Pesticide pollution of water resources as a result of agricultural operations is a global issue (Jusoh et al. 2013; Eunji et al. 2018; Saleh et al. 2020). In addition to the fossil fuels, human activities have also resulted in the pollution of water sources and eventually loss in ecosystem function and endanger human health (Mojiri et al. 2020; Manasa and Mehta 2020; García-García et al. 2015). Pesticides have varying health effects depending on their chemical composition. Numerous pesticides on the market today are composed of organophosphorus compounds. While some organophosphorus compounds are extremely toxic to humans, they generally degrade rapidly in the environment and have been rarely detected in groundwater (Laksaci et al. 2017; Tolmacheva et al. 2018; Kılıç et al. 2020).

Deltamethrin is a synthetic pyrethroid insecticide that kills insects both directly and indirectly via digestion. It is used for a variety of crops throughout the year, and as a result, it is abundant in the environment. Additionally, it is non-biodegradable after six months of storage at 40 °C, stable when exposed to atmospheric oxygen, and undergoes isomerization when exposed to sunlight (Hassan et al. 2013). Numerous methods for pesticide removal from aqueous solutions have been developed involving physical, chemical, and biological technologies including precipitation with coagulation (Zolgharnein et al. 2011), membrane filtration (Farrukh et al. 2014; Musbah et al. 2018), and photochemical degradation (Sakkas et al. 2010). Despite the abundance of available treatment techniques, adsorption technology has been widely used to remove organophosphorus pesticides due to its low capital cost, simplicity of design, high removal efficiency, insensitivity to toxic substances, and ease of operation (Hokkanen et al. 2016). The adsorption process using activated carbon is the most efficient and promising fundamental technique for waste water treatment. Commercial activated carbons are expensive and require elaborate reactivation and regeneration processes to achieve precise surface properties (Zhiyuan et al. 2020; Streat et al. 1995; Li et al. 2009; Babel and Kurniawan 2003; Kanel et al. 2006). These processes frequently result in the degradation of the carbon's adsorption properties and impairing the operation's economic viability. As a result, low-cost adsorbents capable of being used in large-scale water decontamination processes are required. These adsorbents could be waste generated in large quantities that can be used directly or after transformation into more active products in adsorption processes (Memon et al. 2008; Mojiri et al. 2019). The use of low-cost agricultural waste byproducts such as coconut leaves (Ramlah et al. 2016), banana peels (Jamil et al. 2008), orange peel (Moreno-Pirajá and Giraldo 2012), coffee shells (Acosta et al. 2016), corn straw (Zeng et al. 2018), tobacco stems (Chen et al. 2017), and rubber seed shells (Thanchonok et al. 2015) has also been investigated as alternatives to activated carbon for pesticides removal. The main objective of this paper is to develop a low-cost activated adsorbent from African walnut shells (AWS) to remove deltamethrin from contaminated water streams and evaluate the influence of operating conditions using equilibrium and isotherms models.

Experimental

Chemicals and standards

Analytical-grade deltamethrin insecticide was acquired from Sigma-Aldrich with a 98% purity having a molecular weight of 505.20 g/mol. The structure, identity, and physicochemical properties of deltamethrin are illustrated in Table 1. Other chemical reagents including hydrochloric acid, sodium hydroxide, potassium hydroxide, and spectroscopic grade methanol were obtained from Merck Company. A stock solution of deltamethrin pesticide with a concentration of 200 ppm was prepared. Methanol: water was used to prepare the solution (60:40 v/v) as the pesticide has a low solubility in water, after which dilutions of 5 ppm, 10 ppm, 15 ppm, 20 ppm, 25 ppm and 30 ppm were made and used as the working standard solutions. Spectroscopic-grade methanol was used as blank for all absorption measurements. A UV-Spectrum analysis was carried out to determine the best wavelength for measurement. The absorbance was measured at 280 nm for calibration curve determination through the UV–Vis spectrophotometer (Shimadzu UV-1700).

Table 1 Properties of deltamethrin insecticide
Full size table

Preparation of adsorbent

The African walnut shells (AWS) were obtained in Nigeria from a retail store. After being washed with distilled water, they were put in an oven and dried at a temperature of 105 °C for 24 h. The shells were grounded and sieved using a SPEX miller machine to achieve a particle size of 0.6 mm. To turn the substance into a fine powder to be heated using a muffle furnace, the substance was first carbonized at 600 °C over for 2 h. The carbonized samples were mixed in potassium hydroxide (KOH) with an impregnation ratios of 1:1 and 2:1 (KOHAWS1 and KOHAWS2, respectively) for 12 h and dried at 105 °C. In order to increase the porosity and surface area of the substance, further chemical treatment was carried out by heating at 800 °C under the N2 atmosphere flow for 3 h. Acid washing was conducted by soaking the prepared samples for 2 h in 0.1 HCl and washed severely to a neutral pH with distilled water and then oven-dried at 110 °C to achieve a constant weight. Oven-dried samples were kept in the dessicator until further analysis.

Characterization of adsorbent

Surface morphology of a material is determined by scanning electron microscope (SEM) which shows micrograph of the material with different pores, structures, and sizes in micrometer. SEM micrographs of AWS (without activation), KOHAWS1, KOHAWS2 were obtained using SEM JEOL JSM—6610LV at the same diameter. The spectra of AWS before and after activation were determined using a Fourier transform infrared spectroscopy (FTIR) (Nicolet 6700 Thermo Electron) to identify the kind of surface functional groups responsible for pesticide binding. The Brunauer–Emmett–Teller (BET) surface area analysis via the micrometrics (Microactive for Tristar II plus version 2.02, Quantachrome instrument) was used to measure the surface area (m2/g), pore volume (cm3/g), and pore diameter (nm) of the adsorbents by the N2 adsorption–desorption isotherms models. The materials were pre-heated at 150 °C by nitrogen adsorption and oven-dried for 16 h before the tests, after which the samples were degassed for 5 h at 300 °C. The BET method was used to determine the surface area of the adsorbents and in calculating the micropore and mesopore surface area in accordance with the IUPAC classifications. The Barret–Joymer–Hanlenda (BJH) method was used to determine the volume and pore size distribution in the mesopore range. A pH drift method was used to identify the adsorbent’s point of zero charge (Williams and Aydinlik 2018). 0.15 g of KOHAWS was weighed into a sealed bottle containing 0.1 M NaCl and shaken at 200 rpm for 24 h. for initial pH between 2 and 12. The suspensions were then centrifuged, and the final pH (pHf) after filtration was measured by using a pH meter (Mettler Toledo).

Batch adsorption experiments

Batch sorption analysis was carried out using sealed containers by preparing 250 mL deltamethrin solutions at initial 5–25 mg/L concentrations. In each of the sealed bottles, 0.1 g of adsorbents was added (KOHAWS1 and KOHAWS2) and kept in a mechanical water bath shaker at a constant temperature with an agitation speed of 150 rpm for stabilization. These were shaken at different time intervals (5, 10, 20, 30, 45, 60, 75, 90, 120 min) until equilibrium was reached. The quantity of deltamethrin adsorbed at time, t was calculated as shown in Eq. (1). The UV–VIS spectrophotometer (Shimadzu UV-1700) was used to evaluate deltamethrin concentrations in the solution at wavelength of 280 nm before and after adsorption. At an initial pesticide concentration of 5 ppm and 0.1 g adsorbent, the pH influence on deltamethrin adsorption onto AWS was studied at the pH range of 2–10. With the addition of aliquot portions of 0.1 M HCl and 0.1 M NaOH solutions, the initial pH values were adjusted. Solutions were kept in sealed bottles and placed for 24 h of contact time in a water bath shaker at 150 rpm at 30 °C. The solutions were then filtered with a 0.45-μm syringe filter, and the final residual concentrations were measured by a UV–Visible spectrophotometer. To investigate the effect of adsorbent dosage, sorbent doses at 0.04 g, 0.08 g, 0.12 g, and 0.16 g were used under same equilibrium conditions. The effect of agitation speed was also determined in the range of 80–200 rpm under equilibrium conditions.

$$ q_{t } = \frac{{\left( {C_{O} - C_{t} } \right)V}}{W} $$
(1)

where qt denotes the amount of deltamethrin adsorbed at time t; Co and Ct (mg/L) denote the deltamethrin concentrations at starting concentration and time t (min), respectively. The final volume is V (L), and the mass of sorbent is denoted by W (g).

Desorption studies

After the batch sorption experiments, the KOHAWS loaded with deltamethrin was collected and gently washed with distilled water to eliminate un-adsorbed deltamethrin. The KOHAWS was separated from the suspension by filtration with 0.45-µm filter. 1 g of the deltamethrin loaded KOHAWS was mixed with three desorption solvents (acetone, acetonitrile, and ethyl acetate) and was shaken in a mechanical water bath for 90 min which is the studied equilibrium time at pH 6 with speed of 150 rpm. The concentration of the deltamethrin was estimated spectrophotometrically. The desorbed KOHAWS was repeatedly washed with distilled water and oven dried for 12 h at 105 °C. The desorption studies were carried out for 3 consecutive cycles for regeneration and reusability of the KOHAWS.

Analysis of data

Adsorption capacity and removal efficiency

Deltamethrin removal efficiency by AWS was determined using Eq. 2, where Co (mg/L) and Ce (mg/L) are the deltamethrin concentrations at initial and at equilibrium. As stated in Eq. 3, qe (mg/g) is the quantity of deltamethrin adsorbed at equilibrium. In this equation, V (L) is final solution volume, and W (g) is sorbent mass.

$$ {\text{Removal efficiency}} \left( \% \right) = \frac{{\left( {C_{o} - C_{e} } \right)}}{{C_{0} }} \times 100 $$
(2)
$$ q_{e} = \frac{{\left( {C_{O} - C_{e} } \right)V}}{W} $$
(3)

Adsorption isotherm models

Freundlich, Halsey, Harkin–Jura, Temkin, and Langmuir isotherm models were chosen to explain the deltamethrin adsorption mechanism in the equilibrium onto AWS. In multilayer adsorption, the Freundlich isotherm is a mathematical model that describes the non-uniform distribution of adsorption heat and affinity throughout the heterogeneous surface (Zhao et al. 2018). The nonlinear and linear forms of the Freundlich isotherm model (Freundlich 1906) can be mathematically represented in Eqs. 4 and 5.

$$ q_{{\text{e}}} = K_{{\text{f}}} C_{{\text{e}}}^{1/n} $$
(4)
$$ \log q_{{\text{e}}} = \log K_{{\text{F}}} + \left( \frac{1}{n} \right)\log C_{{\text{e}}} $$
(5)

where the quantity of deltamethrin adsorbed is qe (mg g−1); the Freundlich constants are denoted by Kf (mg g−1) and 1/n, which are measurements of sorption capacity and Freundlich exponent, respectively.

The regression coefficient (R2) and the root mean square error (RMSE) were also used to identify the best fitting model and validity of the models, respectively. The RMSE as expressed by Nazari et al. (2016) is shown in Eq. 6.

$$ {\text{RMSE}} = \sqrt {\frac{{\mathop \sum \nolimits_{n - 1}^{n} (q_{{\text{e}}} \cdot \exp - q_{{\text{e}}} \cdot {\text{cal}})^{2} }}{n}} $$
(6)

where n is the number of experimental data and qe is the amount of deltamethrin adsorbed (mg/g). The Langmuir isotherm model assumes a monolayer adsorption (Miyah et al. 2018; Langmuir 1918), and the linear form of the isotherm is mathematically expressed in Eqs. 7 and 8.

$$ q_{{\text{e}}} = \frac{{Q_{{\text{m}}} KC_{{\text{e}}} }}{{1 + KC_{{\text{e}}} }} $$
(7)
$$ \frac{{C_{e} }}{{q_{e} }} = \frac{1}{{KQ_{m} }} + \frac{{C_{e} }}{{Q_{m} }} $$
(8)

where Ce represents the deltamethrin equilibrium concentration (ppm) (mg L−1), qe represents the quantity of deltamethrin adsorbed (mg g−1), Qm represents the maximum sorption capacity (mg g−1) denoted as 1/slope, and K represents the Langmuir constant (L/mg).

As illustrated in Eq. 9, the dimensionless separation factor for equilibrium parameter, RL, is a significant criterion in the simulation of the Langmuir isotherm (Miyah et al. 2018).

$$ R_{{\text{L}}} = \frac{1}{{1 + bC_{i} }} $$
(9)

where Ci is the optimal starting concentration of deltamethrin and b is the Langmuir constant (L mg-1) (ppm). The type of the adsorption process and the form of the isotherm may be determined by the values of RL. Unfavorable (RL > 1), linear (RL = 1), favorable (0 < RL < 1), and irreversible (RL = 0) adsorption processes are represented by the value of RL.

The Halsey isotherm is another isotherm model that is associated with multi-layer adsorption at a distant from the surface of an adsorbent (Malekbala et al. 2015). Equation 10 illustrates the linear form of the Halsey isotherm.

$$ q_{{\text{e}}} = \frac{1}{{n_{{\text{H}}} }}\ln K_{{{\text{H}} }} - \left( \frac{1}{n} \right)\ln C_{{\text{e}}} $$
(10)

where nH and KH are the Hasley isotherm constants.

The Harkin–Jura isotherm model was also used to describe the adsorption process. The model also assumes a multi-layer adsorption on the sorbent surface possessing heterogeneous distribution. The linear form of the model is expressed mathematically as shown in Eq. (11).

$$ \frac{1}{{q_{{\text{e}}}^{2} }} = \frac{B}{A} - \left( \frac{1}{A} \right)\log C_{{\text{e}}} $$
(11)

The Harkin–Jura constants are B and A. The Harkin–Jura constants were determined by plotting 1/qe2 versus log Ce in a linear form.

The Temkin isotherm model predicts that as the adsorption surface increases, the thermal adsorption of all molecules decreases linearly, and that the adsorption has a constant dispersion of binding energy up to maximum binding power. The equation for Temkin isotherm is expressed in Eq. 12.

$$ q_{{\text{e}}} = \frac{{{\text{RT}}}}{{b_{{\text{T}}} }} \ln A_{{\text{T}}} + \left\{ {\frac{{{\text{RT}}}}{b}} \right\}\ln C_{{\text{e}}} $$
(12)

where AT is the Temkin isotherm equilibrium binding constant (L/g), bT denotes the Temkin isotherm constant, R denotes the universal gas constant (8.314 J/mol/K), T denotes the temperature at 298 K, and B denotes the heat of sorption constant (J/mol).

Adsorption kinetics

To find the best fit for the experimental data, the pseudo-first- and second-order models were used. Equation 13 and Eq. 14 illustrate the mathematical form of the pseudo-first-order (Lagergren 1898) and pseudo-second-order models (Ho and Mckay 1999), respectively.

$$ \log \left( {q_{{\text{e}}} - q_{t} } \right) = - \frac{{K_{1} }}{2.303}t + \log (q_{{\text{e}}} ) $$
(13)

where K1 is the pseudo-first-order rate constant of the sorption (min−1); qe and qt are the amounts of sorbate sorbed by the sorbent at equilibrium and time t (mg/g).

$$ \frac{t}{{ q_{t} }} = \frac{1}{{k_{2} q_{{\text{e}}}^{2} }} + \frac{1}{{q_{{\text{e}}} }}t $$
(14)

where 1/qe is the slope, 1/k2qe2 is the intercept, and K2 is the rate constant (g/mg min).

Results and discussion

Adsorbent characterization

Scanning electron microscopy (SEM)

Scanning electron microscopy (SEM) was used to examine the adsorbents surface morphology. The SEM micrograph was analyzed at 10 µm in diameter. The images obtained illustrate the amorphous nature of AWS with various shapes and sizes as well as heterogeneous morphology. Figure 1a presents the SEM image of AWS before KOH activation with which the pores distribution was not visible. After activation, the micrograph of KOHAWS1 showed an irregular pore distribution and shape as shown in Fig. 1b. The SEM image of KOHAWS2 showed similar heterogeneous porous nature with a fine rounded sphere, rounded cavities with a diameter 10 µm as shown in Fig. 1c. The results are consistent with previous studies (Williams et al. 2020; Abdelhameed et al. 2021; Tang et al. 2020).

Fig. 1
figure 1

SEM images of a AWS (before KOH activation), b KOHAWS1 after activation, and c KOHAWS2 after activation

Full size image

Fourier transformed infrared spectroscopy (FTIR)

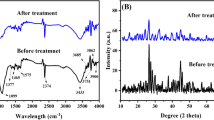
The appearance of a large number of peaks at different locations on the adsorbents in the FT-IR spectrum indicates the complex chemical nature of the material. The FTIR spectrum of the AWS before activation as shown in Fig. 2a showed a strong broad peak around 3674 cm−1 and 3432 cm−1 which indicates the presence of O–H stretching of alcohol groups (Diel et al. 2021; Wang et al. 2021). The peak around 1610 cm−1 is due to the C=C stretching of conjugated alkenes. The spectra bands at 1028 cm−1 are attributed to a C–N stretching of amine groups. KOHAWS1 showed functional band groups assigned to O–H stretching vibrations of phenols and alcohols in the region of 3356 cm−1 (Chen et al. 2017), the spectrum is assigned to acyclic C=C bonds around 1648 cm−1, and the bands around 1052 cm−1 correspond to C–O stretching for primary alcohol as shown in Fig. 2b. The spectra showed a sharp peak band of O–H stretching vibration at 3395 cm−1 for alcoholic and phenolic groups after increasing the activating agent. The band about 1635 cm−1 also corresponds to primary amine N–H stretching for KOHAWS2; the relatively extreme band at around 1230 cm−1 is assigned to the stretching vibrations of the aromatic ester C=O bonds (Çiğdem and Yunus 2018; Hu et al. 2021; Hamadeen et al. 2021) as shown in Fig. 2c. The oxygen groups found in the AWS include carbonyl groups, ethers, esters, alcohols, and phenol groups from the band allocations. The results obtained confirm the existence of functional groups such as alcohol, carbonyl, carboxylic, and ether groups that may play an important role in the pesticide binding process.

Fig. 2
figure 2

FT-IR spectra of a AWS (Without activation), b KOHAWS1 and c KOHAWS2

Full size image

pH point of zero charge

The adsorption mechanism is not always an electrostatic attraction between the sorbent and the sorbate. Therefore, the pH point zero charge (pHPZC) is used to confirm whether the adsorption mechanism follows an electrostatic interaction or another mechanism such as complexation, dissolution or precipitation (Rasaie et al. 2021; Alikhani et al. 2021). The ∆pH (pHfinal – pHinitial) was plotted against the initial pH to determine the pHPZC. The pH where the ∆pH was zero was taken as the pHpzc. pHPZC of KOHAWS1 and KOHAWS2 was 7.4 and 7.6, respectively, as shown in Fig. 3a and Fig. 3b, respectively.

Fig. 3
figure 3

pH point zero charge of a KOHAWS1 and b KOHAWS2

Full size image

Brunauer–Emmett–Teller (BET) analysis

The N2 adsorption–desorption isotherm models and the BET technique were used to examine the surface area of the activated AWS (Bruanuer et al. 1938). As shown in Table 2, AWS has a high SBET (353.02 m2/g), and the surface area (SBET) increased following activation with KOH. KOHAWS1 had a SBET of 812.23 m2/g and a pore volume of 0.123 cm3/g, whereas KOHAWS2 had a SBET and pore volume of 814.42 m2/g and 0.343 cm3/g, respectively. The increased pore volume of the sorbent signifies a rapid deltamethrin adsorption onto the KOHAWS. Figure 4a, b and Fig. 5a, b show the N2 adsorption–desorption graphs of AWS and KOHAWS, as well as the related BJH pore size distribution plots. It was also discovered that the activated AWS N2 adsorption–desorption isotherm models are a mixture of Type II and Type IV isotherms (Thommes et al. 2015). Type II is defined by physisorption with form, which is the consequence of unconstrained monolayer coverage up to a high P/Po. Mesoporous adsorbents are illustrated by Type IV isotherms. The adsorbent adsorptive interactions as well as the interactions between the molecules in the condensed form influence the adsorption characteristics in mesopores. Thus, the study reveals that the average pore distribution for all the adsorbents was in the mesopore range (2–50 nm) which is strongly evident in the pore size distribution as reported in the IUPAC classification (Thommes et al. 2015; Wang et al. 2021; Alikhani et al. 2021). The presence of a mesoporous structure is necessary to enhance the deltamethrin removal efficiencies.

Table 2 BET Surface are analysis before and after activation
Full size table
Fig. 4
figure 4

N2 adsorption–desorption isotherm for a AWS (before activation) and b KOHAWS (after activation)

Full size image
Fig. 5
figure 5

Pore size distribution of a AWS (before activation) and b KOHAWS (after activation)

Full size image

Effect of pH

The solution pH can have a major impact on the efficiency because it affects the surface charge density of the sorbent and therefore the interactions between the sorbate and the sorbent (Nazal et al. 2021; Chen et al. 2017; Zeng et al. 2018). The pHPZC of KOHAWS1 and KOHAWS2 were determined to be 7.4 and 7.6, respectively, as stated in the preceding section. Adsorption in acidic or basic solutions would be determined by the properties of the sorbent and the analyte. The efficacy of the adsorption is largely reliant on the solution pH. At an initial pesticide concentration of 5 ppm and 0.1 g adsorbent, the pH influence on deltamethrin adsorption onto AWS (KOHAWS1, KOHAWS2) was studied at the pH range of 2–10. As shown in Fig. 6, the removal efficiency was seen to be low at pH 2 (66.2%) for KOHAWS1 but gradually increased with increasing pH until pH 6.0 which had the highest percentage of 97.4% and thereafter decreases gradually in alkaline pH to 73.1%. Similarly, for the pH effect of sorption of deltamethrin onto KOHAWS2, it was observed that pH 2 had the lowest percentage removal of 58.1% and increased until it reached equilibrium at pH 6 with a high removal efficiency of 98.2%. The analysis typically showed that the adsorbed quantity of the deltamethrin onto AWS increases with an increase in solution pH. Therefore, the pH of the solution influences the carbon surface charge and the electrolyte dissociation or protonation (Vassileva et al. 2016; Bedin et al. 2016). These results suggest that at a solution pH lower than the pHPZC, the external surface charge becomes positively charged which would favor an electrostatic interaction.

Fig. 6
figure 6

Effect of solution pH on deltamethrin removal efficiency of KOHAWS1 and KOHAWS2

Full size image

Effect of contact time and initial concentration

The contact time is an important parameter that influences the removal efficiency and verifies the kinetics of the process (PraiseGod et al. 2017). As shown in Fig. 7a, the amount of deltamethrin adsorbed by the KOHAWS1 and KOHAWS2 sorbent was calculated at different initial concentrations of 5, 10, 15, 20, 25 mg/L. The effects of contact time and initial concentrations of deltamethrin on adsorption using KOHAWS1 and KOHAWS2 have shown that deltamethrin adsorption increases with time until it reaches equilibrium and a constant value after which no further deltamethrin is extracted from the solution. Deltamethrin adsorption was rapid at the initial stages of the contact period, as shown in Fig. 7a and Fig. 7b, and slowed down near equilibrium. As a consequence of the high affinity of the interacting groups on the surface of the activated carbon formed (Yu et al. 2014), deltamethrin adsorption was rapid. The high initial adsorptive rate at the starting point was caused by the adsorption of deltamethrin by the adsorbent’s exterior surface. The amount adsorbed at equilibrium (qt) increased from 11.1 to 40.375 mg g−1 for KOHAWS1 with an initial concentration increase from 5 to 25 mg/L as shown in Fig. 7b For KOHAWS2, the amount adsorbed at equilibrium (qt) increased from 11.138 to 42.625 mg g−1. The removal efficiency reduced from 88.8% at 5 mg/L to 64.6% at 25 mg/L highest concentration for KOHAWS1, while there was an increase in removal efficiency from 68.2% at 5 mg/L to 89.1% at 25 mg/L indicating 5 mg/L initial concentration having the highest removal efficiency which was used for equilibrium studies.

Fig. 7
figure 7

Effect of contact time and initial concentration on the adsorption of deltamethrin onto a KOHAWS1 and b KOHAWS2

Full size image

Effect of adsorbent dosage

The sorbent dosage also affects the adsorption capacity of the adsorbent for a given initial concentration. Commonly increasing adsorbent dosage improves adsorption efficiency. The results as shown in Fig. 8 reveal removal efficiency of deltamethrin was increased by an increase in sorbent dosage. KOHAWS2 had the highest removal efficiency of 98.65% with 0.16 g sorbent dose, while KOHAWS1 had efficiency with 0.16 g sorbent to be 96.58%. The increase in removal efficiency with increasing sorbent dosages is probably due to the greater amount of AWS for activation as well as the surface area and pore volume available at higher sorbent dose, providing more active sorption sites resulting in a higher removable percentage (Thanchanok et al. 2015; Yi et al. 2013).

Fig. 8
figure 8

Effect of the adsorbent dosage on deltamethrin removal

Full size image

Effect of agitation speed

Under equilibrium conditions, the impact of agitation speed was measured in the range of 80–200 rpm. Figure 9 illustrates the highest adsorption occurred at 150 rpm with an overall removal efficiency of 88.6% and 86.8% for KOHAWS2 and KOHAWS1, respectively. Removal efficiency initially improved with increasing sample speed, but then started to decrease at higher speed. From these observations, it can be inferred that the adsorption was greatly affected by the agitation speed. This may also be ascribed to increased turbulence and as a result a reduction in the depth of the boundary layer surrounding the particles of the sorbent as a result of increased agitation (Bilal et al. 2016).

Fig. 9
figure 9

Effect of agitation speed on deltamethrin removal

Full size image

Adsorption isotherms

The equilibrium sorption isotherm essentially expresses the basic relationship at a given temperature between the sorbate concentration and its extent of accumulation on the sorbent surface. The linear forms of the isotherms and parameters of the models of Langmuir, Freundlich, Halsey, Harkin–Jura, and Temkin are shown in Table 3. The Langmuir isotherm as plotted in Fig. 10a and Fig. 10b shows that KOHAWS1 and KOHAWS2 had a coefficient (R2) of 0.9969 and 0.9852, respectively, and which showed a maximum sorption capacity of 57.64 mg/g. For the dimensionless separation factor of the adsorption of deltamethrin onto AWS, it can be deducted that KOHAWS1 and KOHAWS2 had a RL values of 0.290 and 0.348, respectively, indicating a favorable adsorption process (Williams and Aydinlik 2018). The regression coefficient (R2) as shown in Fig. 11a and Fig. 11b for Freundlich isotherm models and the root mean square error (RMSE) were also used to identify the best fitting model and validity of the models, respectively, as shown in Table 3. A linear plot of ln qe versus ln Ce shows a regression coefficient (R2) of 0.9609 for KOHAWS1 and regression coefficient (R2) of 0.9533 for KOHAWS2 for Halsey isotherm model as shown in Fig. 12a and Fig. 12b. Multilayer sorption on the interface of sorbent with a heterogeneous pore structure is assumed in the Harkin–Jura isotherm model. The Harkin–Jura constants were obtained from the linear plot of 1/qe2 against log Ce. According to the results obtained as shown in Fig. 13a, the regression coefficient (R2) for KOHAWS1 is 0.7349 while that of KOHAWS2 is 0.8409 as shown in Fig. 13b.

Table 3 Freundlich, Langmuir, Halsey, Harkin–Jura, and Temkin isotherm parameters for deltamethrin adsorption onto AWS at 30 °C
Full size table
Fig. 10
figure 10

Langmuir isotherm for a KOHAWS1 and b KOHAWS2

Full size image
Fig. 11
figure 11

Freundlich isotherm for a KOHAWS1 and b KOHAWS2

Full size image
Fig. 12
figure 12

Halsey isotherm for a KOHAWS1 and b KOHAWS2

Full size image
Fig. 13
figure 13

Harkin–Jura isotherm for a KOHAWS1 and b KOHAWS2

Full size image

Adsorption heat of all molecules reduces linearly with increasing monolayer coverage in the Temkin isotherm model, which assumes equivalent binding affinity and homogeneous distribution of adsorbed heat (Srivastava et al. 2020). Plotting the quantity sorbed (qe) against lnCe results in a linear graph for determining the Temkin constants. According to the plotted graphs in Fig. 14a, b, it was observed that the regression coefficients (R2) for KOHAWS1 and KOHAWS2 were 0.9865 and 0.9651, respectively. From the experimental data, it is evident that Langmuir model fits better (R2 of 0.9969 and 0.9852 for KOHAWS1 and KOHAWS2, respectively) than Freundlich model (R2 of 0.9791 and 0.9823 for KOHAWS1 and KOHAWS2, respectively. These findings are consistent with recent studies (Spessato et al. 2021; Viera et al. 2021; Nazal et al. 2021; Spessato et al. 2021). The isotherm models which express a multi-layer adsorption (Harkin–Jura and Halsey isotherm model) do not fit with the experimental data. This is an indication that the adsorption model represents a monolayer adsorption with KOHAWS2 having the highest sorption capacity of 57.64 mg g−1.

Fig. 14
figure 14

Temkin isotherm for a KOHAWS1 and KOHAWS2

Full size image

Adsorption kinetics

The sorption equilibrium also provides information on the adsorption process kinetics. The kinetics of the sorption process is important for inferring effectiveness and determining the kind of adsorption mechanism based on the physico-chemical characteristics of the adsorbent and pesticide. In this research, the pseudo-first-order (PFO) and pseudo-second-order (PSO) kinetics were used to test which was best fitted with the experimental data. The PFO entails a linear plot of log (qe − qt) versus t as shown in Fig. 15a, b for KOHAWS1 and KOHAWS2, as shown in Fig. 7a, b, which indicate a rise in deltamethrin removal for all initial pesticide concentrations tested. It can be deducted that at the initial time, the adsorption rate was faster but steadily decreased with time before equilibrium was reached. This may be due to the fact that the active sites available on both adsorbents appear to be saturated gradually over time, thus slowing the adsorption of deltamethrin to the bulk of the activated carbon. The PFO and PSO kinetics data for both KOHAWS1 and KOHAWS2 are provided in Table 4. The PFO model was more evident at the initial concentration of 5 ppm with a regression coefficient (R2) of 0.989 and 0.995 for KOHAWS1 and KOHAWS2, respectively, and pseudo-rate constant (K1) values of 0.0081 min−1 and 0.0082 min−1 for KOHAWS1 and KOHAWS2, respectively. According to Table 4, the regression coefficient (R2) for all deltamethrin concentrations for the PFO was higher than for the PSO model. The PFO model can also be used explicitly to differentiate deltamethrin concentration and qe values from both the experimental data and the measured data used to test the model (Vithanage et al. 2016). The parameters which were calculated from deltamethrin adsorption onto KOHAWS1 and KOHAWS2 show more correlation with the PFO kinetics but could not be fitted with the PSO kinetics model. These findings are consistent with recent studies (Hu et al. 2021; Wang et al. 2021; Rigueto et al. 2021; Rasaie et al. 2021; Diel et al. 2021). This may also be seen in the larger values of the PFO rate constant (K1) compared to PSO rate constant (K2). The best fitting of experimental data to the PFO model assumes that physisorption interactions can be more attributed to deltamethrin adsorption onto the sorbent (Vithanage et al. 2016), and adsorption also depends on deltamethrin initial concentration. When the initial concentration is more comparable to surface coverage, the PFO kinetics are also highly applicable (Azizian 2004).

Fig. 15
figure 15

Pseudo-first-order kinetic model for a KOHAWS1 and b KOHAWS2

Full size image
Table 4 Results comparison between PFO and PSO kinetic models
Full size table

Desorption and reusability

The reusability of KOHAWS is significant for the adsorptive removal for real waste water application. It was found that acetone had the highest recovery efficiency (94.56%) while acetonitrile (73.1%) and ethyl acetate (51.4%) are not good desorption solvents according to this study as shown in Fig. 16a. It was also observed that the recovery efficiencies slightly decreased from 91.2 to 68.5% after three cycles as shown in Fig. 16b. The slight decrease in the recovery efficiencies may be attributed to the loss of some of the adsorption sites during the regeneration process (Mandal and Singh 2017).

Fig. 16
figure 16

a Desorption of deltamethrin by different solvents. b Reusability of the KOHAWS

Full size image

Possible adsorption mechanism

Sorbent surface charge density

In general, adsorption of pesticides by an adsorbent involves a series of steps involving the migration of adsorbate from the aqueous state to the solid phase. Cations adsorb better on negatively charged surfaces, while anion adsorption is easier on positively charged surfaces. The adsorption mechanism is not always an electrostatic interaction between the adsorbate and adsorbent; pHpzc is basically used to explain whether the adsorption follows an electrostatic interaction or another mechanism (Duranoğlu and Beker 2012; Eunji et al. 2018). According to the present study, deltamethrin removal may be affected by sorbent-sorbate interaction due to electrostatic attraction. At a solution pH < pHpzc, the external surface charge becomes positive which would favor an electrostatic interaction. Therefore, the cationic deltamethrin could be strongly adsorbed onto the negative AWS via electrostatic attraction indicating that the adsorption of deltamethrin onto AWS is pH dependent.

Performance evaluation: adsorbate–adsorbent interaction

However, adsorption is not solely dependent on physical or chemical factors but rather a mixture of both. Adsorption mechanisms are affected by a variety of factors. Parameters such as sorbate solubility, sorbent specific surface area, and sorbate molecular mass have a significant impact on the sorbent–sorbate interaction. According to Table 5, this study used parameters like the sorbate solubility, the specific surface area of the sorbent (SBET), sorbent quantity (q mol/g), and sorbate preferential sorption (qP). Effective surface area (eSBET) has been introduced as a new attribute in adsorption evaluations along with preferential sorption (qP), which is the fraction of sorbent concentrations in solution to sorbate concentrations on surfaces. Due to the fact that morphological and chemical adsorption is dependent on the amount of pertinent binding sites with a sufficient affinity for sorption regardless of the total SBET of the adsorbent, derivation of eSBET is essential (Ighalo et al. 2020). According to Ighalo et al. (2020), the relationship between eSBET and qP is that as eSBET increases, qP increases. This signifies that new pore is formed and micropores increase as a result of the activation mechanism used and more pores that are active for adsorption develop as well. Because of this, eSBET increases in proportion to the activation. SBET plays an important role in adsorption even though the chemistry of the sorbate–sorbent interface is important. For this present study, the qP, which was used as a key index parameter in determining the magnitude of sorbent–sorbate interactions, was found to have values of approximately 1 for both adsorbents, suggesting that the sorbates had a comparatively higher proclivity for the sorbent over persisting in the solution.

Table 5 Parameters and sorption characteristics of adsorbents
Full size table

Comparison of KOHAWS with other low cost adsorbents for pesticide removal

Under similar operating conditions, the most commonly used low-cost adsorbents for removal of pesticides were compared with the present study. As shown in Table 6, it was observed that the adsorption capacity of KOHAWS was higher than majority of the adsorbents for deltamethrin removal. Additionally, the removal efficiency of KOHAWS is higher than the other adsorbents used for pesticides removal which is an indication that the prepared adsorbent for this study is an auspicious material for removal of deltamethrin and likewise wastewater treatment applications.

Table 6 Comparison of KOHAWS with other adsorbents for pesticides removal
Full size table

Conclusion

This research demonstrates that novel African walnut shells that have been activated and chemically modified are a potential low-cost adsorbent for deltamethrin removal from aqueous solutions. The study revealed a high SBET of 812.23 m2/g and 814.42 m2/g for KOHAWS1 and KOHAWS2, respectively, after KOH-activation. The FTIR spectra analysis shows that the activated KOHAWS contains oxygen groups such as carbonyl, esters, alcohols, and phenol groups which are essential in pesticide removal. Under equilibrium conditions, adsorption data fitted the Langmuir isotherm model with a higher R2 values for both activated sorbents with the highest adsorption capacity at 57.64 mg g−1. According to the experimental data, the kinetics of the study also reveals deltamethrin sorption correlates with the PFO model which points to physisorption mechanism. In addition, the mechanism of adsorption was highly pH dependent, which further proves that electrostatic interactions play a pivotal role in the sorption behavior of the deltamethrin sorption onto KOHAWS. Finally, the findings of this study reveal deltamethrin adsorption onto novel AWS which will serve as a vibrant, cost-effective, low-cost adsorbent for pesticide removal from water and waste water.