Introduction

Derivation tunnels are constructed to derive river flow even in flood condition from the construction area of the dams. After the dam construction, the revaluation of these tunnels for different purposes, e.g., the outlet vent, is very important for economical aspect. However, in the operation, these tunnels in huge dimensions can be exposed to some important damages such as corrosion and cavitation due to high flow velocities and so sub-pressures. To overcome these challenges, the best method is to aerate the flow using aeration devices called as aerators or aeration vent.

Recently, computational fluid dynamics (CFD) method has been widely used to determine the hydrodynamics of the flows in the hydraulic structures. Aydin (2005) and Oztürk et al. (2008) investigated bottom-inlet spillway aerator by using CFD analysis and determined their scale effects comparing some other experimental results. Azimi and Shabanlou (2018) simulated turbulence and flow conditions passing through a side weir and a circular channel in the numerical model under supercritical flow conditions using the Flow 3D software program. When the experimental and numerical results were compared, a good agreement was observed between the results of the side-weir Froude number, flow rate over the side weir and discharge coefficient of the side weir. Aydın and Işık (2015) explained the advantages and disadvantages of experimental studies through examples and also explained the actuality and usability of numerical analysis. Lee et al. (2014) successfully applied the CFD analysis to determine the optimal pitch angle of the Banana Jet Fan. They concluded that when designing the jet fan in the tunnel ventilation, the pitch angle effects of airflow and friction loss must be considered. Akhtari and Seyedashraf (2017) numerically studied the effect of middle vanes on the flow structure in open channels with sharp 60° bends using the standard and RNG k–ε turbulence models. Kumcu (2017) experimentally and numerically investigated the hydraulic characteristics of Kavsak Dam and Hydroelectric Power Plant. The author obtained a good agreement between the physical and numerical models with regard to flow characteristics. The cavitational risk on the spillway was also successfully obtained numerically by two-dimensional CFD model using Flow 3D software. The CFD results indicated more than 10% air concentration, which is sufficient to prevent cavitation. Thanh and Ling-Ling (2015) aimed to predict some characteristics of flow through the spillway with a breast wall by using the physical and numerical modeling. The authors preferred the RNG k–ε turbulence model for their numerical solutions, since it showed more accurately than the standard k–ε model when comparing with the physical model data. Pfister and Hager (2010a, b) presented two comprehensive studies experimentally. They scrutinized the air transport phenomenon and hydraulic design of chute aerators. Aydin (2017) experimentally and numerically investigated the aeration performance of the bottom-inlet aerators for preventing from cavitation. It was concluded that the bottom-inlet aerator’s performance is greater than the conventional aerator for same flow conditions.

In this study, the CFD model with RNG turbulence model was also used to simulate the outlet tunnel and the aerator gallery of Ilısu Dam. For this purpose, firstly the CFD models of the Ilısu Dam outlet with 1/40 scale were performed and the results of the CFD were compared with physical model results to determine CFD model performance. Then, the CFD simulations with 1/40-scaled and full-scaled models (prototype) were performed to estimate scale effects on the Ilısu Dam outlet aeration. Finally, in order to improve the aeration performance of the aerator gallery, new different design was tested using also CFD simulation techniques.

Physical model

The Ilısu Dam taken in consideration in this study was constructed as a concrete-face rock fill dam with 135 m height on Dicle River in Turkey. It was planned that one of huge three derivation tunnels having 12 m diameter and 1000 m length of the dam is converted into the outlet vent to discharge of the reservoir after construction. Another derivation tunnel parallel to this tunnel was considered as aeration tunnel. Two tunnels called as DT1 (aeration tunnel) and DT2 (outlet vent) were connected by a bypass aeration gallery having a horseshoe cross section. The physical model tests with 1/40 scale in this study were carried out in Hydraulic Laboratory of State Hydraulic Works in Turkey (DSI Report 2013). To achieve dynamic similarity with geometric and kinematic similarity, model and prototype must have same length, time and force scale ratio. Dynamic similarity ensures two ways for incompressible flow: If there is no free surface, Reynolds numbers of model and prototype are equal. However, if there is a free surface, Reynolds, Froude and (if necessary) Weber and cavitation numbers of model and prototype are correspondingly equal (White 2003). For the model tests including free surface, exact dynamic similarity is only achieved by equivalent Froude and Reynolds numbers.

$$Re_{\text{m}} = Re_{\text{p}} \Rightarrow \frac{{V_{\text{m}} L_{\text{m}} }}{{\nu_{\text{m}} }} = \frac{{V_{\text{p}} L_{\text{p}} }}{{\nu_{\text{p}} }}$$
(1)
$$Fr_{\text{m}} = Fr_{\text{p}} \Rightarrow \frac{{V_{\text{m}}^{2} }}{{gL_{\text{m}} }} = \frac{{V_{\text{p}}^{2} }}{{gL_{\text{p}} }}$$
(2)

To match Froude and Reynolds numbers, the kinematic viscosity ratio must be as follows:

$$\frac{{\nu_{\text{m}} }}{{\nu_{\text{p}} }} = \frac{{L_{\text{m}} }}{{L_{\text{p}} }}\frac{{V_{\text{m}} }}{{V_{\text{p}} }} = \frac{{L_{\text{m}} }}{{L_{\text{p}} }}\left( {\frac{{L_{\text{m}} }}{{L_{\text{p}} }}} \right)^{1/2} = L_{\text{r}}^{3/2}$$
(3)

in which V is averaged flow velocity, L is length, i.e., hydraulic diameter, g is gravitational acceleration, ν is kinematic viscosity and subscripts m and p represent model and prototype, respectively.

To obtain the exact similarity, it is necessary to use a fluid which provides kinematic viscosity by Eq. (3). In most laboratory tests, this is very difficult or impossible. In practice, the water is used for the physical model tests. The Froude similarity is usually used in free surface flows because the body forces and gravity are dominant. Therefore, the Reynolds number similarity can be neglected because the viscous effects are too low beside the other effects. Typically, Reynolds number of the model is regarded as too small for the range from 10 to 1000. To estimate high-Reynolds-numbers prototype data, an extrapolation curve obtained from low-Reynolds-numbers model data can be used. Using such method, considerable uncertainty in the prototype data estimate is observed, especially for Reynolds numbers higher than 106. However, it was pointed out that there is no choice in hydraulic model testing (White 2003). Therefore, the obscured Reynolds number effects in Froude number similarity will emerge, especially for the small scales of hydraulic models, which are called as scale effects.

On the other hand, when considering air flow in the hydraulic model, the important parameters are the Reynolds and Mach numbers. In this case, the following relation can be obtained for compressible fluids. The compressibility parameters in a gas flow can change in some other parameters such as viscosity and pressure

$$\frac{{V_{\text{m}} }}{{a_{\text{m}} }} = \frac{{V_{\text{p}} }}{{a_{\text{p}} }},$$
(4)

and then from Eq. (1),

$$\frac{{\nu_{\text{m}} }}{{\nu_{\text{p}} }} = \frac{{L_{\text{m}} }}{{L_{\text{p}} }}\frac{{a_{\text{m}} }}{{a_{\text{p}} }},$$
(5)

in which a is acceleration. This requires low viscosity and high speed of sound in air flow model such as wind-tunnel test. Hydrogen may be used instead of the air but it is too expensive and dangerous (White 2003). As can be understood from these explanations, the similarity of air–water flow for hydraulic models is very complicated. The compressibility effects of high-velocity air flow are generally neglected in the hydraulic model tests when using Froude number similarity. The physical model tests (Fig. 1) were performed with Froude numbers similarity with 1/40 scale (DSI Report 2013). Therefore, some scale effects can be expected in the physical model test results, especially in air flow measurements. The model scales with Froude number similarity are given in Table 1.

Fig. 1
figure 1

A view from physical laboratory model (DSI Report 2013)

Full size image
Table 1 Model and prototype scales according to Froude number similarity
Full size table

Numerical model

Governing equations

The continuity and Navier–Stokes equations of fluid motion can be given as follows for incompressible flows in the Cartesian coordinate systems:

$$\frac{\partial }{\partial x}\left( {uA_{x} } \right) + \frac{\partial }{\partial y}\left( {vA_{y} } \right) + \frac{\partial }{\partial z}\left( {wA_{z} } \right) = 0$$
(6)
$$\begin{aligned} & \frac{\partial u}{\partial t} + \frac{1}{{V_{F} }}\left[ {uA_{x} \frac{\partial u}{\partial x} + vA_{y} \frac{\partial u}{\partial y} + wA_{z} \frac{\partial u}{\partial z}} \right] = - \frac{1}{\rho }\frac{\partial p}{\partial x} + G_{x} + f_{x} \\ & \frac{\partial v}{\partial t} + \frac{1}{{V_{F} }}\left[ {uA_{x} \frac{\partial v}{\partial x} + vA_{y} \frac{\partial v}{\partial y} + wA_{z} \frac{\partial v}{\partial z}} \right] = - \frac{1}{\rho }\frac{\partial p}{\partial y} + G_{y} + f_{y} \\ & \frac{\partial w}{\partial t} + \frac{1}{{V_{F} }}\left[ {uA_{x} \frac{\partial w}{\partial x} + vA_{y} \frac{\partial w}{\partial y} + wA_{z} \frac{\partial w}{\partial z}} \right] = - \frac{1}{\rho }\frac{\partial p}{\partial z} + G_{z} + f_{z} \\ \end{aligned}$$
(7)

In the equations, ρ is the water density; Ax, Ay and Az are the fractional area open to flow in the x-, y- and z-directions, respectively; u, v and w are the components of flow velocity in the x-, y- and z-directions, respectively, VF is the volume fraction open to flow; Gx, Gy, Gz are body acceleration components; and fx, fy, fz are viscous acceleration components.

The CFD solver uses Volume of Fluid (VOF) scheme to describe interaction of two-phase (air–water) flow. For a cell in the domain, if volume fraction F = 0, the cell is full with a phase (i.e., air); if F = 1, then the cell is full with the other phase (i.e., water); and if 0 < F < 1, the cell contains an interface between two phases (i.e., free surface). The VOF formulation based on Hirt and Nichols (1981) for two-phase flows is defined as follows:

$$\frac{\partial F}{\partial t} + \frac{1}{{V_{F} }}\left[ {\frac{\partial }{\partial x}\left( {FA_{x} u} \right) + R\frac{\partial }{\partial y}\left( {FA_{y} v} \right) + \frac{\partial }{\partial z}\left( {FA_{z} w} \right)} \right] = 0$$
(8)

Turbulence model

CFD codes introduce several turbulence models based on analytical or/and experimental approaches in the literature. According to many researchers in the literature, renormalized group (RNG) turbulence model (Yakhot and Smith 1992; Yakhot and Orszag 1986) is most favorable model in the hydraulic applications. In this model, some statistical approaches are implemented to derive the averaged equations for turbulence quantities, e.g., turbulent kinetic energy (k) and its dissipation rate (ε). Although this model’s equations are similar to those of standard k–ε model, the equation constants determined empirically are obtained explicitly in the RNG model. The RNG model can be especially preferable to define low-intensity turbulence flows and flows having strong shear regions more accurately (FLOW-3D 2014). The governing equations of RNG turbulence model for k and ε are given below:

$$\frac{\partial k}{\partial t} + u_{j} \frac{\partial k}{{x_{j} }} = \frac{\partial }{{\partial x_{j} }}\left[ {\left( {\nu + \frac{{\nu_{t} }}{{\sigma_{k} }}} \right)\frac{\partial k}{{\partial x_{j} }}} \right] + G - \varepsilon$$
(9)
$$\begin{aligned}\frac{\partial \varepsilon }{\partial t} + u_{j} \frac{\partial \varepsilon }{{x_{j} }} &= \frac{\partial }{{\partial x_{j} }}\left[ {\left( {\nu + \frac{{\nu_{t} }}{{\sigma_{\varepsilon } }}} \right)\frac{\partial \varepsilon }{{\partial x_{j} }}} \right] + C_{\varepsilon 1} \frac{\varepsilon }{k}G \\&\quad- C_{\varepsilon 2} \frac{{\varepsilon^{2} }}{k} - C_{\mu } \eta^{3} \frac{{1 - \eta /\eta_{0} }}{{1 + \beta \eta^{3} }}\frac{{\varepsilon^{2} }}{k}\end{aligned}$$
(10)

where ν is kinematic viscosity and eddy viscosity can be obtained by Eq. (11):

$$\nu_{t} = C_{\mu } \frac{{k^{2} }}{\varepsilon }$$
(11)
$$G = \nu_{t} \left( {\frac{{\partial u_{i} }}{{x_{j} }} + \frac{{\partial u_{j} }}{{x_{i} }}} \right)\frac{{\partial u_{i} }}{{\partial u_{j} }}$$
(12)
$$\eta = \frac{k}{\varepsilon }\sqrt {\frac{G}{{\nu_{t} }}}$$
(13)

Constants in the RNG equations are given as β = 0.012, ηo = 4.38, Cµ = 0.085, Cε1 = 1.42, Cε2 = 1.68, σk = σε = 0.72.

Boundary conditions and mesh generation

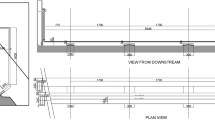
The geometry and boundary condition of the model are illustrated in Fig. 2. In the simulations, high-resolution structured mesh was used to ensure mesh independences of the analysis results as shown in Fig. 3. The numerical models were performed with 1/40-scale and prototype dimensions (full-scaled). Two-phase turbulent flow model with Navier–Stokes equations was considered in the numerical solutions. Solution convergence was achieved approximately in the flow times of 8 s for 1/40-scaled model and 80 s for prototype dimensions. The timescale is 6.32 for Froude number similarity as seen in Table 1.

Fig. 2
figure 2

CFD model geometry and boundary conditions

Full size image
Fig. 3
figure 3

Mesh structures of the numerical model

Full size image

Results and discussions

Verification of numerical model

Some experimental data of 1/40-scaled model were presented to identify the numerical uncertainties of the numerical model with the same scale. Figure 4 illustrates some view of some numerical results from the CFD analyses. The outputs in this figure demonstrate that the numerical results were physically realized. The aeration performances of the outlet tunnel obtained from physical and numerical model (1/40 scaled) are presented in Table 2. In this table, Ht is water head in the reservoir, Hmax is maximum reservoir head, D is diameter of outlet tunnel, A is cross-sectional area of outlet tunnel, V is mean velocity of water flow, Q is water discharge in the tunnel, β is air entrainment rate and subscripts of w, a and m represent water, air and model, respectively. As seen from Table 2 and Fig. 5, while there are big differences up to 49% between the CFD and experimental results for low discharge, the difference is reduced to 2% for higher discharges. The mean relative error approximately is 20% for 1/40-scaled model. The reason for the differences may be due to selected mesh structures, turbulence model and errors of measurement devices in the experiments. In the numerical computing, the flow is supposed to be fully turbulent, but the viscous effects are dominant at low discharge for the physical model studies that the values are low. In particular for low discharge, the numerical results may be more sensitive to the mesh structures. If the finer mesh is used for low discharge, the results may be more compatible. However, the more the cell elements, the more the computational effort and time. Therefore, an optimal mesh size was used for computational effort and accuracy.

Fig. 4
figure 4

Views from CFD analysis of the Ilısu outlet and aerator

Full size image
Table 2 CFD and experimental results for 1/40-scaled model
Full size table
Fig. 5
figure 5

Comparison of experimental and numerical results for 1/40-scaled model: a air entrainment discharge, b air entrainment rate

Full size image

The results from CFD analyses with the model and the prototype dimensions are plotted in Fig. 6 to see the scale effects between the model (scaled 1/40) and the prototype. The differences seen in these graphs are probably due to scale effects, because except for the scale, all the specifications of model and prototype in the numerical simulations are designed as the same. The scale effects were determined from 8.6 to 23.6% for maximum and minimum flow discharges, respectively. The ranges of Reynolds numbers are Re = 1.6 × 105–3.2 × 105 for model and Re = 42 × 106–81 × 106 for prototype. It is generally accepted that if Reynolds number is lower than 105, the scale effects can be neglected. Pinto (1988) also stated that the scale effects for 1/8 scale will not occur if Reynolds number is lower than 3.3 × 105. When evaluated together these information, for a 1/40-scaled hydraulic model, considerable scale effects, as seen in Fig. 6, can be expected.

Fig. 6
figure 6

Model–prototype comparison for CFD results: a air entrainment discharge, b air entrainment rate

Full size image

Original design

In order to understand the aeration mechanism in air gallery, velocity vectors along longitudinal sections of air gallery are given for different outlet flows in Fig. 7. The air passes from DT1 to DT2 tunnel due to negative pressure created by high-velocity water jet from box-sectioned conduits in DT2 tunnel. The velocities in the gallery can reach 20 m/s. From the analysis results of 1/40-scaled model and prototype, it is seen that the velocities on the profiles approximately agree with Froude similarity scale for velocity (1/\(\sqrt {40}\)). While the maximum velocities in the gallery occur above of the gallery, the minimum velocities were observed in the two corners of the gallery. The stagnant corners cause a decrease in aeration performance to restrict the air entrainment. In order to understand better the air transport in the gallery, the air velocity contours on the cross sections in Fig. 8 are presented in Fig. 9 for the maximum water discharge. As seen in these sections, the maximum velocities occur above at the beginning of the gallery due to the momentum effects of the air entering from bottom. The minimum velocity also formed at bottom of the gallery in section A which corresponds to beginning of the gallery. Then, the air velocity is more uniform in the following sections with a low velocity core in middle of the second half of the gallery. These distributions on the section indicate a seconder helicoidal flow along the gallery. This mechanism required an improvement in the design of the aeration gallery to provide better aeration efficiency.

Fig. 7
figure 7

Air velocity contours of prototype for different water discharges along aeration gallery

Full size image
Fig. 8
figure 8

Cross sections along the aeration gallery

Full size image
Fig. 9
figure 9

Air velocity contours at the different section of prototype air gallery (Qw = 764 m3/s)

Full size image

Enhanced designs

Two new enhanced designs were developed to improve the aeration performance of the aerator gallery. In first enhanced design, a box section having the same cross-sectional area as the original section was used. The box-sectioned aeration gallery connects two tunnels (DT1 and DT2) from the top side using two curves. In this way, the increase in aeration efficiency was intended eliminating stagnant regions from the corners of the original design. The first enhanced design of the gallery is shown in Fig. 10a. The aeration mechanism of the enhanced design no 1 (EDN-1) is displayed for different water discharges in Fig. 11. The figures show that the velocities in the gallery increase with the water discharge in the main outlet tunnel. As similar to original design, while the maximum velocities were seen above of the gallery, the minimum velocities occur below of the gallery at the first half part of the gallery. However, unlike the original design, there are no stagnant regions in the elbows because the curve connections divert the air flow from DT1 to the gallery and from the gallery to DT2 tunnel. Therefore, more uniform and efficient aeration was ensured by this new enhanced design.

Fig. 10
figure 10

Enhanced designs of the aeration gallery: a design no 1, b design no 2

Full size image
Fig. 11
figure 11

Velocity contours of enhanced design no 1

Full size image

In another enhanced design, the two main tunnels (DT1 and DT2) are directly connected by a gallery having original horseshoe cross section (Fig. 10b). The velocity profiles on longitudinal section of the enhanced design no 2 (EDN-2) are also given in Fig. 12 for different water discharges. As similar to the other design results, while increasing the water discharge in DT2 tunnel, the air flow velocities in the gallery also increase considerably. Figure 12 points out that EDN-2 provides higher and more uniform velocity distribution than the other designs along the gallery.

Fig. 12
figure 12

Velocity contours of enhanced design no 2

Full size image

The air entrainment rates for the all designs are given comparatively in Table 3 for the all designs. This table indicated that EDN-1 is 50% more efficient than the original design, and EDN-2 provides 100% more efficient approximately. The aeration performance results are also plotted comparatively in Fig. 13a, b. The increments in the aeration performance were seen clearly in these figures. The average air concentration can be calculated by \(C_{\text{o}} = \beta /(1 + \beta )\). Russell and Sheehan (1974) stated that latest 5% air concentration was required for preventing cavitational damage. Aydin et al. (2018) also reported from detailed literature review that the required air concentration is approximately 6–8% to protect cavitation damage. In this study, while the mean air concentration is determined as 37% for the original design, it is determined as 46% and 54% for EDN-1 and EDN-2, respectively that is considerably higher than the limits for avoiding the cavitation. But the aim of the aeration in the outlet is not only the cavitational damage but also the other uses such as pressure reduction and corrosion. So it can be stated that more aeration brings more usefulness. According to the results and explanations, it is clear that EDN-2 is the most effective design among the all designs (Fig. 14).

Table 3 Comparison of aeration performance of the original and enhanced designs
Full size table
Fig. 13
figure 13

Aeration performance of enhanced designs: a air entrainment rate versus dimensionless head, b air discharge versus water discharge

Full size image
Fig. 14
figure 14

Views from CFD analysis of enhanced designs: a EDN-1, b EDN-2

Full size image

Conclusions

In this study, the original design of an outlet tunnel and its aeration system was analyzed using CFD models with model and prototype dimensions. Then, determining the defects of the original design, two new enhanced designs have been proposed to improve the aeration efficiency of the aeration system. The obtained results from the study were outlined below:

  1. 1.

    The analysis of multiphase mixture model such as air–water flow is very complex both experimentally and numerically. The CFD method used can successfully model the two-phase flows in the outlet and aeration system. The CFD results were quite useful to determine and then eliminate the scale effects. The numerical results agree with the scaled physical model for high water discharge but there are some deviations for low water discharges.

  2. 2.

    Considering Reynolds numbers ranges of 1.6 × 105–3.2 × 105 for 1/40-scaled model and 42 × 106–81 × 106 for prototype, significant scale effects can be expected in the model studies. The scale effects due to 1/40 scale were determined from 8.6 to 23.6% for maximum and minimum flow discharges respectively obtained from the CFD analyses of model and prototype.

  3. 3.

    The results show that the two new designs, EDN-1 and EDN-2, considerably improved the aeration performance of the aeration gallery by approximately 50% and 100%, respectively. Therefore, it can be stated that EDN-1 is the best design in respect to aeration efficiency and economical.

It is also concluded that the model studies are very difficult and expensive for huge water structures. Since the experimental models also require small scales, the scale effects are inevitable especially for multiphase flow such as air–water mixture flows. The results show that CFD simulation which is very flexible may be a good alternative. It is concluded that the CFD technics can helps the engineers to design the hydraulic structures with real dimensions discarding scale effects. But anyways, the deficiency of the numerical models should be regarded in the analysis.