Introduction

Sedimentation in reservoirs is an outcome of constructing an obstruction in a flowing river, which results in an abatement of the transport capacity of river. The capacity of reservoir diminishes due to silt aggregation and altered sediment balance due to erosion of river downstream. Reservoir sedimentation represents a serious threat to the storage available. Globally, the annual loss rates relative to installed capacity are generally estimated to range between 0.5 and 1% (Mahmood 1987; White 2001; Basson 2009; Schleiss et al. 2010). Pakistan is confronting major issue of sedimentation which is continuously depleting the useful storage of reservoirs. Indus river system has three reservoirs, i.e. Chahsma, Tarbela and Mangla. As per hydrographic survey of 2011–2012, reservoir capacities of Chashma and Terbella have reduced to 60 and 35% of gross storage capacity. Whereas the reservoir capacity for Mangla Reservoir after raising of Mangla dam has been reduced to 1% of gross storage capacity (Pakistan Water and Power Development Authority 2012). All reservoirs trap a portion of the sediment load carried by inflows and, therefore, will experience a continuous reduction in storage volume. The sediment deposition has unfavourable impact, for example, increase in back water level, formation of shoals. Due to the increase in sedimentation flow, regulation diminishes and eventually the reservoir could not achieve its objectives like irrigation, flood mitigation and hydropower generation etc. For a sustainable use of reservoir, it will be necessary to regulate the flows and effective sediment management should be carried out. Since the last few years number of numerical models have been developed and utilized to investigate the reservoir sedimentation problems in rivers and natural streams. Zeleke et al., (2013) used SRH-1D model to predict the sediment inflow to Angereb dam reservoir. The simulation results were in good agreement with the measured sediment deposition in the reservoir. One-dimensional numerical model GSTARS-3 developed by Yang and Simoes (2002) based on theory of minimum stream power has some additional features that it can be applied for determination of channel width while keeping depth as a known parameter for given hydraulic and sediment routing conditions.

Yang and Simoes (2002) applied GSTARS-3 model for simulation of sedimentation and delta movement in Terbela Reservoir in Pakistan. The profile of the bed simulated using GSTARS-3 was in good agreement with the measured profile. In the present study, GSTARS-3 (Generalized Sediment Transport for Alluvial Ricers) sediment transport model along with GIS software was used to determine (1) sediment inflow to Chashma Reservoir, (2) sediment pattern and rate of deposition in the Chashma Reservoir and (3) to explore the ways to enhance the life of reservoir based on various operational scenarios for sediment management.

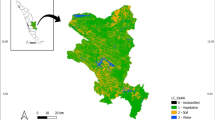
Location of the study area

The Chashma Barrage is situated on the Indus River at a distance of 56 km from Jinnah Barrage. The barrage supplies water to the Chashma Jhelum Link (CJ Link) Canal on the left bank and Chashma Right Bank Canal (CRBC) on the right bank. Chashma Barrage has shallow reservoir with some storage component, original gross storage capacity of the reservoir was 0.87 MAF (1.073 BCM) with live and dead storage of 0.72 MAF (0.888 BCM) and 0.15 MAF (0.185 BCM), respectively. Five hydrographic surveys of Chashma Reservoir were carried out since the operation of reservoir started. The hydrographic surveys of Chashma Reservoir revealed that capacity of the reservoir is depleting vigorously due to sediment deposition. Location plan of Chashma Reservoir and reduction in reservoir capacity are shown in Fig. 1. The maximum and minimum designed reservoir levels are 649 ft. (197.81 m) and 638.15 ft. (194.51 m), respectively. The last hydrographic survey in 2011–2012 showed that the gross capacity depleted to 0.348 MAF (0.429 BCM), live capacity to 0.231 MAF (0.285 BCM) and dead storage as 0.117 MAF (0.144 BCM) (ISRIP-WAPDA). The problem of Chashma Reservoir is that it is indiscriminately being filled up and drawdown several times each year without respect to its response to this treatment. Sand bars developed in front of the barrage in the form of delta. The delta has spread to the barrage like a braided stream. Analysis of hydrographic survey shows that process of bela and active river channels formation has almost stabilized. Growth of weeds and bushes on belas stabilized the sediment layers. Additionally, during low flow season the gates of the barrage are closed to provide water to the hydle power station. Because of this, the water upstream of barrage ponded up and sediments started settling down.

Fig. 1
figure 1

Location plan of Chashma Barrage

Full size image

Methodology

The processes involved in this study include data collection, data analysis and selection of suitable transport model. Calibration of the model is done before hydraulic and sediment routing computation for Chahsma Reservoir. GSTRAS-3 is capable of performing hydraulic and sediment routing computations both in longitudinal and lateral directions. Furthermore, it is also capable of computing channel geometry with fixed or movable boundary conditions.

Data collection

Following necessary data were collected and used for GSTARS3 sediment transport model:

Geometry data

Cross-sectional geometry was defined by X–Y coordinate which is a lateral location and bed elevation. Lateral locations (X) were given using a reference point for each cross section, and the coordinate pair was entered in order of increasing X coordinate, i.e. starting from the left-hand side of the cross section and marching towards the right-hand side (looking downstream). In this study, 15 cross sections were used to cover entire reservoir for modelling purposes.

Hydrological data

Hydrological data include water discharges, temperatures and water surface elevations. Daily discharge data for Chashma Barrage for the year 1971–2012 was collected from surface water hydrology project (SWHP), WAPDA. Mean annual flow for Chashma Reservoir is 117,000 ft3/s (3313 m3/s) whereas the peak annual discharge is 313,627 ft3/s (8881 m3/s). Discharge required for flushing of reservoir should be twice of mean annual flow available. Therefore, flushing of Chahsma Reservoir was performed for an available discharge of 2,340,000 ft3/s (6626 m3/s). Flushing discharge is available during flood season for two months, i.e. July–August.

Sediment data

Sediment data comprise of bed gradation data and sediment inflow hydrograph. Bed gradation data and suspended sediment load data for D/S of Jinnah Barrage was collected from WAPDA and sediment gradation curve for suspended load was plotted. Particle size distribution at D/S of Jinnah Barrage showed that suspended sediment load comprises of 18% clay, 75% silt and 7% of sand. Sediment inflow to Chahsma Reservoir is specified in terms of sediment rating curve downstream of Jinnah Barrage. The measured suspended sediment load data for the period of 2012–2013 has been used for developing the sediment rating curve which is used as inflow boundary condition at downstream of Jinnah Barrage as shown in Fig. 2.

Fig. 2
figure 2

Sediment rating curve

Full size image

Calibration of model

The model was calibrated by simulating the observed sediment deposition from the year 1971 to 2008. By slightly adjusting the Manning’s “n” value and using eight-sediment transport function, a good agreement between measured and simulated values can be found. Figure 3 shows calibration for the Chashma Reservoir thalweg profile using eight-sediment transport function. Out of the eight-sediment transport function, Yang’s (1973 + 84) sediment transport function gave more closer results to actually observed thalweg profiles. Reservoir capacity computed using Yang’s 1973 + 84 sediment transport function is 0.3283 which is 2.28% more than the actually observed capacity of reservoir in 2008. Figure 4 shows the thalweg profile of reservoir using Yang’s 1973 + 84 sediment transport function.

Fig. 3
figure 3

Performance of various sediment transport functions in estimating the bed levels

Full size image
Fig. 4
figure 4

Calibration of the model using Yang’s 1973 + 84 sediment transport function for the year 1971–2008

Full size image

Validation of model

The validation of model is done to evaluate its performance by using the parameters which were adjusted during calibration process. The validation of model is performed by using the bathymetry data for the year 2008 to 2012 using Yang’s 1973 + 84 sediment transport function. After simulation, the reservoir capacity computed is 0.321 MAF which is 7.71% lesser than the capacity computed using hydrographic survey in 2012. Figure 5 shows the validation of Chashma Reservoir.

Fig. 5
figure 5

Validation of the model using Yang’s 1973 + 84 sediment transport function for the year 1971–2008

Full size image

Results

After calibration and validation model was applied for future application from 2013 to 2054 for five different operational scenarios. The adjusted GSTARS3 model was applied for 10-, 20- and 42-year simulation period. The results of above five scenarios are as follows:

Scenario-1

In scenario no. 1, flow and pond level values of the last 42 years were repeated for future prediction of Chashma Reservoir storage capacity. The storage capacity computed for 10, 20 and 42 years of simulation was 0.285 MAF (0.352 BCM), 0.264 MAF (0.326 BCM) and 0.233 MAF (0.287 BCM). This showed that the capacity of reservoir would be depleted to 73% of gross storage capacity after 42 years of simulation. The change in bed elevation for 10, 20 and 42 years of simulation is shown in Fig. 6. However, it is reasonable to compare the GSTARS-3 results with HEC-RAS results for Chashma Reservoir which shows that the capacity of reservoir would be depleted to 0.245 (0.302 BCM) MAF while operating under existing conditions (Shah 2010).

Fig. 6
figure 6

Simulation results for scenario-1

Full size image

Scenario-2

In scenario no. 2, flow values of the last 42 years were taken for simulation period. Besides this, pond level was kept at 638.15 ft. for 15 days (1st July–15th July) to see the trends for sediment flushing. The storage capacity computed after 10, 20 and 42 years of operation was 0.393 MAF (0.485 BCM), 0.414 MAF (0.511 BCM) and 0.429 MAF (0.529 BCM). The results of scenario-2 revealed that the capacity of reservoir would recover to 23% of gross storage capacity after 42 years of operation while considering 15 days flushing. The change in bed elevation and sediment trap efficiency for 10-, 20- and 42-year simulation period is shown in Fig. 7.

Fig. 7
figure 7

Simulation results for scenario-2

Full size image

Scenario-3

In scenario no. 3, flow values of the last 42 years were taken for simulation period. Besides this, pond level was kept at 638.15 ft. for 30 days (1st July–30th July) to see the trends for sediment flushing. The storage capacity computed after 10, 20 and 42 years of operation was 0.435 MAF (0.537 BCM), 0.440 MAF (0.543 BCM) and 0.476 MAF (0.587 BCM). The results of scenario-3 revealed that the capacity of reservoir would recover to 37% of gross storage capacity after 42 years of operation while considering 30-day flushing. The change in bed elevation and sediment trap efficiency for 10-, 20- and 42-year simulation period is shown in Fig. 8.

Fig. 8
figure 8

Simulation results for scenario-3

Full size image

Scenario-4

In scenario no. 4, flow values of the last 42 years were taken for simulation period. Besides this, pond level was kept at 638.15 ft. for 45-day flushing (1st July–15th August) to see the trends. The storage capacity computed after 10, 20 and 42 years of operation was 0.501 MAF (0.618 BCM), 0.538 MAF (0.664 BCM) and 0.579 MAF (0.714 BCM). The results of scenario-4 revealed that the capacity of reservoir would recover to 66% of gross storage capacity after 42 years of operation while considering 45-day flushing. The change in bed elevation and sediment trap efficiency for 10-, 20- and 42-year simulation period is shown in Fig. 9.

Fig. 9
figure 9

Simulation results for scenario-4

Full size image

Scenario-5

In scenario no. 5, flow values of the last 42 years were taken for simulation period. Besides this, pond level was kept at 638.15 ft. for 60 days flushing (July–August) to see the trends. The storage capacity computed after 10, 20 and 42 years of operation was 0.594 MAF (0.733 BCM), 0.601 MAF (0.741 BCM) and 0.644 MAF (0.794 BCM) (85% Gross storage capacity). The change in bed elevation and sediment trap efficiency for 10-, 20- and 42-year simulation period is shown in Fig. 10.

Fig. 10
figure 10

Simulation results for scenario-5

Full size image

Discussion

Performance of GSTARS3 sediment transport model was assessed statistically using MAPE, Nash–Sutcliffe efficiency and R2. Nash–Sutcliffe efficiency is a statistical tool which is used to compare the simulated results with the actually observed bathymetric survey data. NSE values for calibration and validation of sediment transport model were found as 0.64 and 0.45 with the coefficient of determination 0.67 and 0.70. The difference between measured and simulated thalweg for calibration and validation of sediment transport model was found as 0.55 and 1.5%. Yang (2008) compared the sediment simulation results of Tarbela Reservoir with the bathymetric survey in Pakistan and concluded that the error less than 20% is acceptable between the measured and simulated results.

GSTARS-3 software is capable to determine the amount of sediment accumulated in the reservoir as well as the amount of sediments that exit the river reach. Amount of sediments deposited in the Chashma Reservoir during calibration and validation of model were 9.283 × 108 and 9.437 × 108 Ton, respectively. However, it is reasonable to compare this with Terbela Reservoir in Pakistan where amount of sediments entered into the reservoir were 1.01 × 1010 Ton from 1976 to 1994. Similarly, the amount of sediments deposited in Tapu Reservoir in Thailand was 2.3 × 106 Ton from 1987 to 1990. Both of these reservoirs were also modelled using GSTARS-3 sediment transport model.

Sediment trap efficiency was computed for 10-, 20- and 42-year simulation period for all the five scenarios and then compared with Brune curve for normal ponded reservoir as shown in Table 1. Intensive research studies based on field data were carried out in India to verify validity of Brune curve for Matatila, Hirakhud, Bhakra and Gandhi Sagar Reservoirs (Batuca and Jordaan 2000). Brune curve overestimated the trap efficiency for the first two reservoirs.

Table 1 Sediment trap efficiencies
Full size table

Integrating GSTARS3 results to GIS software

The results obtained from GSTARS3 simulation were incorporated to GIS software to visualize sediment accumulation in the reservoir. Delta formation was observed just 1.0 km from main barrage portion. Therefore, two sections had been selected from fifteen sections where most of the sedimentation took place, i.e. cross section number 1 and cross section number 19. Cross section 1 and cross section 19 exist at a distance of 3 and 8.5 km from main barrage portion. A digital elevation model (DEM) was generated by combining the geometry output from GSTARS-3 model. Figure 11a, b showed the elevation of Chashma Reservoir during calibration and validation of sediment transport model. Figure 11a showed that the elevations of points at section 1 and section 19 in year 2008 range between 620–648 ft. (188.97–197.51 m) and 624–644 ft. (190.19–196.29 m). Whereas, for validation elevation of section 1 and section 19 ranges between 613–645 ft. (186.84–196.59 m) and 617–637 ft. (188.06–194.16 m). The bed elevation of Chashma Reservoir for validation was lowered than the calibration results. This is just because of the super flood in 2010. After the super flood of 2010, the capacity of the Chashma Reservoir was improved. Figure 11c showed that the elevation of Chashma Reservoir for 10, 20 and 42 years of simulation for scenario 1 ranges between 604–634 ft. (184–193.24 m), 599–625 ft. (182.58–190.5 m) and 598–634 ft. (182.27–193.24 m) for section 1 and 614–639 ft. (187.14–194.77 m), 599–635 ft. (182.57–193.55 m) and 604–634 ft. (184–193.24 m) for section 19. This showed that the elevation of Chashma Reservoir increases during 42 years of operation under existing conditions for future prediction of reservoir capacity. The results of scenario-1 showed that only 27% of gross storage capacity is left. Figure 11d showed the elevation for scenario-II considering 15 days of flushing. The bed elevation of Chashma Reservoir after 42 years of operation decreased from 609 to 598 ft. (185.62–182.27 m) for section 1 and 614–604 ft. (187.14–184 m) for section 19. Figure 11e showed the elevation of Chashma Reservoir for 30 days flushing considering scenario-III. The elevation of points further decreased from 606 to 588 ft. (184.71–179.22 m) for section 1 and 616–595 (187.76–181.35 m) for section 19. Figure 11f showed the elevation for Chashma Reservoir for 45 days flushing decreased from 606 to 594 ft. (184.71–181.05 m) for section 1 and 611–600 ft. (186.23–182.88 m) for section 19. Similarly, for scenario-V considering 60 days of flushing the elevation of points further decreased and ranges between 607 and 583 ft. (185–177.70 m) for section 1 and 617–604 ft. (188–184 m) for section 19 as shown in Fig. 11g. The figure showed the change in cross section of reservoir as per change in reservoir elevation. Furthermore, sediment movement towards the power channel increased which can cause negative impacts on long term power generation.

Fig. 11
figure 11

Simulated bed profiles of Chashma Reservoir using various scenarios

Full size image

Conclusions

Following are the conclusions drawn from this study:

  1. 1.

    Average sedimentation rate in reservoir till 2012 is estimated as 0.0124 MAF/year (0.015 BCM/year).

  2. 2.

    The storage capacity of Chashma Reservoir would deplete to 0.233 MAF (0.287 BCM) (73% loss) in the year 2054 for scenario-1 (under existing conditions).

  3. 3.

    Scenario-2 is more effective as 23% of reservoir capacity was recovered after 15 days of flushing and sediment trapped in the reservoir was lesser than the other flushing scenarios. The trap efficiency for Scenario-2 ranges between 43 and 11%.

  4. 4.

    Depositional patterns in Chashma Reservoir showed that sediment movement towards the power channel increases. This would cause the negative effect on the power generation and also wear and tear of turbines.