Introduction

The adverse effects of pharmaceutical residues in the aquatic environment have become an issue for the whole world (Margot et al. 2013; Halling-Sorensen et al. 1998).

Presence of pharmaceutical residues in wastewater and surface water has been proven for many years by several studies (Bercu et al. 2008; Cunningham et al. 2009; Jones et al. 2004; Heberer 2002; Nanaki and Kyzas 2015). They are detected at low concentrations, ranging from µg L−1 to ng L−1. Even though that these concentrations are very low and are difficult to detect, they have adverse impact on human health and environmental (Daughton and Ternes 1999). Elimination rate of the pharmaceutical substances varies according to the process employed; such as activated carbon filtration, UV treatment followed by biological treatment. Moreover, adsorption clay offers a large cation exchange capacity, high specific surface area and a significant swelling (Chen et al. 2008). The objective of this work is to make a contribution in the field of treatment of water by testing adsorption of three molecules (NAP, IBU, CBZ) onto clay mixture smectite and kaolinite, on base of different parameters to evaluate the adsorption performance, the kinetics of the adsorbent and the adsorption isotherms were studied to comprehend the adsorption processes.

Materials and method

Presentation of materials

Natural clay (CB) was collected from Jbel Sejnane (north east of Tunisia) and purified by mixing the clay frequently with NaCl solution to obtain a homo-ionic Na-clay noted (CP) (Chen et al. 2008). This step was performed by shaking 4 g of clay with 120 cm3 of a NaCl (1 M), then centrifuging the suspensions (Lopez-Ramon et al. 1999).

This process was repeated seven times. The Na-clay was then washed many times with distilled water. This cleaning was stopped when the AgNO3 test for chloride ions was negative. After drying at 60 °C, the clay was crushed and sieved through less than 100 μm to get of the very fine particles (<2 µm). The specific surface area (Ss) and cation exchange capacity (CEC) were measured by the BET and Metson methods, respectively (AFNOR NF X 31e130).

The pH of the point of zero charge (pZC) has been determined according to a method previously described in the literature (Lopez-Ramon et al. 1999), 50 mL of a 0.01 M NaCl solution was first placed in a series of amber vials. The pH was then adjusted to successive initial values between 2 and 12, by adding either HCl or NaOH and the clay (0.15 g) was added to the solution. The final pH, reached after 48 h, is measured and plotted against the initial pH. The pH at which the curve crosses the line pH (final) = pH (initial) is taken as the pH of the given adsorbent.

Three pharmaceuticals were selected in this research as target compounds: carbamazepine (an antiepileptic), ibuprofen and naproxen (analgesics), the molecular structure and physicochemical properties of these pharmaceuticals are summarized in Table 1.

Table 1 Molecular structure and main physicochemical properties of studied pharmaceuticals
Full size table

Ibuprofen, naproxen and carbamazepine solutions with different concentrations were prepared by diluting the stock solution in ultra-pure water. NAP, IBU and CBZ concentrations were determined using the absorbance (at 230, 220 and 271 nm, respectively) of the solutions using the UV spectra of the solution by a spectrophotometer (model of SP-3000 Plus).

The X-Ray diffraction pattern of the clay was recorded by X’Pert PRO MPD working on monochromatic radiation Copper Kα1 (1.5406 Å). A counter (PM 8203) records a signal proportional to the intensity of the diffracted beam. The chemical composition of clay is performed by spectroscopy of emission out of gun plasma ICP PERKIN ELMER 3300. The spectroscopic studies were performed using a scanning electron microscopy (SEM, JSM.6300).

Adsorption experiments

All the adsorption experiments were carried out at (298 ± 0.2 K), by batch adsorption. Stock solutions of pharmaceuticals were prepared as 50 mg L−1 by dissolution in ultrapure water. Individual batch adsorption experiments were carried out by shaking 25 mg of clay with 25 mL of pharmaceuticals solution in a series of reagent flasks at a constant speed (250 rpm) in a mechanical shaker for 6 h and centrifuged at 4000 rpm after the samples were separated with the aid of a syringe nylon microfilter (0.45 µm), and the concentration of each solution was measured by spectrophotometer at the corresponding wavelength. The pH of pharmaceuticals solution was adjusted with (0.1 M) HCl or (0.1 M) NaOH.

Adsorption isotherm

To identify the mechanism of the adsorption process, the adsorption isotherm values were evaluated and analyzed. Different isotherm models are available in the literature. Simple, reliable, and widely used models, such as linear, Langmuir, and Freundlich isotherms, were used in this present study. The chosen isotherm models were applied to establish the relationship between the amount of pharmaceuticals adsorbed by the clay and its equilibrium concentration in the aqueous solution. The equilibrium studies were carried out using 25 mg of clay in 25 mL of pharmaceuticals aqueous at different concentrations. The sorption capacity of the clay was evaluated by the amount of pharmaceuticals aqueous adsorbed using the following expression:

$$Q = \frac{{{(}C_{\text{0}} - C_{\text{e}} {) \times }V}}{M}\varvec{ }$$
(1)

where, Q is the amount of solute retained per mass unit of the adsorbent (mg g−1), C 0 and C e are the initial and equilibrium concentration of pharmaceuticals in the solution (mg L−1).

M is the amount of sorbent (g), and V is the volume of the solution (L).

The percentage of the pharmaceuticals was evaluated as follows:

$$R\,(\%) =\frac{(C_{\text{0}} - C_{\text{e}}) \times 100}{C_{\text{0}}}$$
(2)

The Langmuir model assumes that the adsorbent surface is homogeneous and contains only one type of binding site, so the energy of adsorption is constant, which is presented by the following equation:

$$Q_{e} = \frac{{K_{L} \cdot Q_{e} \cdot C_{e} }}{{\left( {1 + (K_{L} \cdot C_{e} )} \right)}}$$
(3)

The linear form of Langmuir adsorption isotherm can be expressed as follows:

$$\frac{{C_{\text{e}} }}{{Q_{\text{e}} }} = \frac{\text{1}}{{Q_{\text{0}} \cdot K_{\text{L}} }} + \frac{\text{1}}{{Q_{\text{0}} }} \cdot \text{ }C_{\text{e}}$$
(4)

where Q 0 (mg g−1) is the Langmuir constant related to the maximum monolayer adsorption capacity and K L (L mg−1) is the constant related to the free energy or net enthalpy of the adsorption (Angove et al. 1997).

The Freundlich model can be applied for multilayer adsorption on a heterogeneous adsorbent surface, with sites that have different energies of adsorption. The Freundlich model is given by the following equation (Freundlich 1906).

$$Q_{\text{e}} = K_{\text{F}} \cdot \left( {C_{\text{e}}^{{\frac{\text{1}}{n}}} } \right)$$
(5)

This expression can be linearized to give the following equation:

$$\text{Ln }\;Q_{\text{e}} = \text{Ln}K_{\text{F}} + \frac{\text{1}}{n} \cdot \text{Ln}C_{\text{e}}$$
(6)

where “K F” (mg g−1) and “n” are Freundlich constants related to adsorption capacity and intensity, respectively.

Dubinin–Radushkevich (DR) isotherm has been used to describe the sorption of drugs onto clay and helps in understanding the type of adsorption (Donat et al. 2005; Hosseini et al. 2003). DR equation can be written as Eq. (7).

The DR equation has the following form

$$\text{ln}\;q_{\text{e}} = \text{ln } q_{\text{s}} - k\varepsilon^{\text{2}}$$
(7)

where q e is DR monolayer capacity (mg g−1), k is a constant related to adsorption energy; q s is the amount of drugs adsorbed per unit weight of adsorbent (mg g−1) and ε is the Polanyi potential, which can be expressed as:

$$\varepsilon = \text{RT}\;\text{ln}\left(1 + \frac{1}{C_{\text{e}}} \right)$$

where C e is the equilibrium concentration of drug in aqueous solution (mg L−1), R is the gas constant and T is the temperature (K), the slope of the line makes it possible to calculate the value of k and the intercept gives the adsorption capacity, q m.

Adsorption kinetics

Kinetic models are helpful in understanding the mechanism of molecule adsorption and in evaluating the performance of the adsorbents. A number of kinetic models have been developed to describe the kinetics of heavy molecule adsorption. In this present study, the kinetic of pharmaceuticals adsorption on the clay were determined with different kinetic models such as the first-order and the pseudo-second order models.

The period of time necessary to reach the equilibrium, previous kinetic experiments were performed. Fixed amounts of adsorbent (25 mg) and volumes of adsorptive solution (25 mL) of initial concentration equal to (50 mg L−1) were kept in contact under shaking (250 rpm) and at constant temperature (T = 298 ± 0.2 K) for different preset time intervals [0–360 min]. Whenever varies in time we take a sample and make it past the centrifuge.

Finally, the supernatant was analyzed by the spectrometer.

The first-order rate equation of the Lagergren is one of the most widely used kinetic models for the adsorption of a solute from a solution (Lagergren 1898). The model has the following form:

$$\frac{{\text{d}Q}}{{\text{d}t}} = K_{\text{1}} \left( {Q_{\text{e}} - Q_{t} } \right)$$
(8)

where Q e (mg g−1) is the amount of the metal ions adsorbed on the adsorbent at equilibrium, and K 1 (min−1) is the rate constant of the first-order adsorption. After integration and application of boundary conditions Q t  = 0 at t = 0 and Q t  = Q t at t = t, the integral form of Eq. (8) becomes the following:

$$\text{Ln}\left( {Q_{\text{e}} - Q_{t} } \right) = \ln Q_{\text{e}} - K_{\text{1}} \cdot t\text{ }$$
(9)

The second-order kinetic model, on the basis of the adsorption equilibrium capacity, is as follows (Hosseini et al. 2003).

$$\frac{{\text{d}Q}}{{\rm d}t} = K_{\text{2}} \left( {Q_{\text{e}} - Q_{t} } \right)^{\text{2}}$$
(10)

where K 2 (g mg−1 min−1) is the rate constant of the second-order equation and Q (mg g−1) is the maximum dye adsorbed. After definite integration through the application of boundary conditions Q t  = 0 at t = 0 and Q t  = Q t at t = t, Eq. (10) becomes the following:

$$\frac{t}{{Q_{t} }} = \frac{1}{{2\left( {Q_{\text{e}}^{2} \cdot K_{2} } \right)}} + \varvec{ }\frac{t}{{Q_{\text{e}} }}$$
(11)

If the second-order kinetic model is applicable, then the plot of \(\varvec{ }\frac{t}{{Q_{\text{e}} }}\) versus t should give a straight line, and Q e and K 2 could be obtained from the slope and intercept of the straight line, respectively.

Sorption thermodynamics

Thermodynamic parameters, including changes in the free energy (ΔG°), enthalpy (ΔH°), and entropy (ΔS°) associated with the adsorption process, can be determined using the following equations (Ho and McKay 1998; Moore and Reynolds 1997).

$$\Delta G{^\circ} = -\,\text{RT}\ln K_{\text{c}}$$
(12)
$$\Delta G{^\circ} = \Delta H{^\circ } - T\Delta S{^\circ }$$
(13)

The plot of LnK c, as a function of \(\frac{1}{T}\), yields a straight line, from which ΔH° and ΔS° can be calculated from the slope and intercept, respectively.

Results and discussion

Characteristics of the clay

Chemical compositions in weight percentage for the raw material denoted as CB, and for the Na-purified clay denoted as CP are given in Table 2.

Table 2 Chemical composition of Jebel Sejnane clay
Full size table

The CEC and SSA for the Na-purified dried clay fraction are 46 meq/100 g, 69.5 m2 g−1.

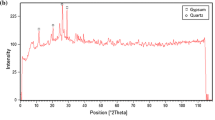
The X-ray diffraction (XRD) of the clay is shown in Fig. 1. The clay contains a mixture of quartz and kaolinite-smectite. Figure 2 shows the FT-IR spectrum of the clay. An intense band located at 1020 cm−1, this band is characteristic of the Si–O stretching vibration of cristobalite. The band at 3700 cm−1 corresponds to the stretching vibration of the hydroxyl groups located between the tetrahedral and octahedral layers of the clay (Leite et al. 2008). The absorption located at 3600 cm−1 and the band near 1650 cm−1 is due to the presence of water molecules adsorbed on the clay structure (Madejova and Komadel 2001). The band at 790 cm−1 may be evidence for the presence of silica and quartz. Other bands located at 920 and 530 cm−1 correspond to deformations of Al–Al–OH and Al–O–Si, respectively (Yaneva and Koumanova 2006). SEM photographs show the textural structural examination of clay before and after the adsorption Fig. 3.

Fig. 1
figure 1

XRD powder of Na-purified clay (CP)

Full size image
Fig. 2
figure 2

FT-IR spectra of Na-purified clay (CP)

Full size image
Fig. 3
figure 3

SEM images of clay and clay after adsorption of pharmaceuticals

Full size image

In Fig. 3a, clay showed a non-homogeneous surface. Also, the surface change in the SEM photograph of the clay after adsorption of drugs indicates the structural changes in the sorbent which is depicted in Fig. 3b.

The point of zero charge (pZC) of the clay used in this study presented in Fig. 4. The clay was observed to possess a point of zero charge (pZC) at a pH(pZC) = 3.78, so its surface has a high affinity for cations at pHs above this value. The surface of the clay was neutral at pH = 3.78.

Fig. 4
figure 4

Zeta potential of clay

Full size image

Effect of contact time

Figure 5 shows pharmaceuticals removal at different contact times using clay as an adsorbent. Pharmaceutical removal increased rather rapidly with the increase of contact time, but then gradually approached a more or less constant value denoting the attainment of equilibrium. The fast kinetics of adsorption during the first minutes of the reaction can be interpreted by the fact that at the beginning of adsorption the number of available active sites on the surface of the adsorbent material is much greater than that remaining after sites a certain time (Stipp 1999). In addition a chemical interaction diffusion and other driving forces can occurred. Besides, the sorption rate decreased due to less sorption as a result of the migration of pharmaceutical cation layer to the interior pore/capillary surfaces. After 240 min, the rate of removal of pharmaceuticals is constant indicate the equilibrium and the non-availability of sorption sites. The maximum adsorption of drugs onto clay was observed at 240 min for CBZ, 240 min for NAP and 180 min for IBU.

Fig. 5
figure 5

Effect of contact time on the adsorption of pharmaceuticals onto the clay (T = 298.0 ± 0.2 °K, pH = 6)

Full size image

Modeling of adsorption isotherm

The kinetic models for adsorption are useful for clarifying the mechanism of adsorption (see Figs. 6, 7).

Fig. 6
figure 6

First-order model equation of pharmaceuticals adsorption

Full size image
Fig. 7
figure 7

Pseudo-second order model equation for pharmaceuticals adsorption

Full size image

The adsorption kinetics of three drugs on clay were investigated using the first-order kinetics and the pseudo-second-order kinetics

According to the results of the correlation coefficients (R) shown in Table 3, we note that the pseudo-second order model is the most reliable way to determine the order of adsorption kinetics for all pharmaceuticals by clay. Furthermore, The values of Q cal calculated by the pseudo-second order model in Table 3; are close to that determined experimentally, which confirms that the adsorption kinetics of the drug onto clay are pseudo-second order.

Table 3 Kinetic parameters for the adsorption of pharmaceuticals onto clay
Full size table

Adsorption isotherms

The objective of the isotherms has been used as the better method in the study of the theoretical aspects of adsorption. The result in Fig. 8 show the influence of the concentration in the ability of pharmaceuticals amount adsorbed which increases with the rise of equilibrium concentration (see Table 4).

Fig. 8
figure 8

Adsorption isotherm on pharmaceuticals onto clay (pH = 6, T = 298.0 ± 0.2 °K)

Full size image
Table 4 Isotherm parameters obtained by fitting equilibrium data with the Langmuir, Freundlich and Dubinin – Radushkevich isotherms for the adsorption of pharmaceuticals on clay
Full size table

The amount of adsorbed naproxen and ibuprofen onto clay is higher than that of carbamazepine, as can be seen, the adsorption efficacy ranking is as follows: naproxen (Q e = 37 mg g−1) > ibuprofen (Q e = 36 mg g−1) > carbamazepine (Q e = 32 mg g−1). This could be due to (pH = 6) carbamazepine is in its neutral form; naproxen and ibuprofen are both protonated. In addition, the surface of the clay is negatively charged, it is reasonable that naproxen–ibuprofen will be absorbed more important than the carbamazepine. According to Fig. 8, we observe that the adsorption isotherms of three pharmaceutical molecules (NAP, IBU, CBZ) onto clay have the same look: the quantity of drugs increases for low concentrations in solution and then attenuated to achieve forme plate corresponding to a saturation of adsorption sites.

The shape of the isotherm pharmaceuticals at pH = 6 is S-type (Cuerda-Correa et al. (2010). Indeed, the isotherms of this class have a concavity facing upward at a low concentration; the adsorbed molecules promote the subsequent adsorption of other molecules. This is due to the interactions between the molecules which are attracted to van der Waals forces.

Sorbent isotherms

Constants of isotherms are commonly used in describing the adsorption equilibrium from aqueous solutions.

The experimental equilibrium data were modeled using the Freundlich model, the Langmuir model and Dubinin–Radushkevich (DR) isotherm model to quantify the adsorption capacity of the adsorbent for the removal of pharmaceuticals.

Figures 9 and 10 show the Freundlich and Langmuir equation obtained by the adsorption of pharmaceuticals onto clay.

Fig. 9
figure 9

Freundlich model for the adsorption of pharmaceuticals onto clay

Full size image
Fig. 10
figure 10

Langmuir model for the adsorption of pharmaceuticals onto clay

Full size image

Figure 11 shown the lnq e against ε 2; the slopes of the line makes it possible to calculate the value of k and the intercept gives the adsorption capacity, q m.

Fig. 11
figure 11

Dubinin–Radushkevich model for the adsorption of pharmaceuticals onto clay

Full size image

The isotherm results obtained for Langmuir, Freundlich and Dubinin–Radushkevich (DR) models are presented in Table 5; On the basis of the correlation coefficient values (R 2), the Freundlich model is the most reliable for the description of the isotherms adsorption than their Langmuir model.

Table 5 Experimental results of thermodynamics of adsorption of pharmaceuticals
Full size table

The (DR) isotherm is more general than the Langmuir and Freundlich isotherm, it was studied to differentiate between the chemical and physical adsorption.

The constant k is used to calculate the mean free energy E (kJ mol−1) defined as the free energy change when 1 mol of ion is transferred to the surface of the solid from infinity in solution (Polanyi 1932; Bering et al. 1972). The equation can be given as follows:

$$E = (2k)^{{\left( { - \frac{1}{2}} \right)}}$$

For drugs sorption onto clay, the mean free energy values obtained in this work (Table 5) are 0.78 kJ mol−1 of ibuprofen, 0.43 kJ mol−1 of naproxen and 0.54 kJ mol−1 of carbamazepine at 298°K. This parameter gives information concerning the nature of adsorption, while the values energy for an ion-exchange mechanism is 8–16 kJ mol−1 (Ho et al. 2001), therefore the adsorption process of three drugs into clay is controlled by physical adsorption.

Effect of pH

Figure 12 shows the effect of pH on the removal of pharmaceuticals, into the clay at different pH values. Generally, the absorptions of pharmaceutical depend strongly on the pH of the solution (Rivera-Jiménez et al. 2010; Bui and Choi 2009).

Fig. 12
figure 12

Effect of pH on the removal of pharmaceuticals onto clay, (C i  = 50 mg L−1, T = 298.0 ± 0.2°K)

Full size image

From the figure, it may be concluded that the retention of drugs is remarkably influenced by the pH. This parameter plays a very important role in the adsorption process, and particularly, in the adsorption capacity. When the pH increased from 4 to 11, the removal of drugs reduced gradually.

The pKa of naproxen and ibuprofen are 4.2 and 4.96, respectively. For basic pH values, the dissociation degree of the surface groups of the adsorbent as well as that of the chemicals is high, so the adsorbent and the solutes occur in their negatively charged forms.

The adsorption of pharmaceuticals onto clay can be leading to an electrostatic repulsion between them. This implies that the adsorption is disfavored. In the case of carbamazepine, it’s a neutral compound in the pH tested range; its binding onto clay is solely attributable to a non electrostatic interaction involving the hydrogen bonding probably through the oxygen groups of esters—and van der Waals interactions (Turku et al. 2007).

Effect of temperature

Figure 13 depicts the adsorption isotherms of naproxen, ibuprofen and carbamazepine at different temperatures. The adsorption isotherms shown in Fig. 13 indicate clearly that the increase of the temperature affects negatively at the adsorption process. Besides, as temperature rises, the adsorption capacity decreases markedly. We noticed that the increase of temperature from 298 to 333 K induces a decrease of the adsorption capacity. The rise of temperature ensures the destabilization of the physical forces involved, so we concluded that there is an optimum value of temperature to promote the adsorption of pharmaceuticals.

Fig. 13
figure 13

Effect of temperature on the adsorption of pharmaceuticals onto clay (C i  = 50 mg L−1, pH = 6)

Full size image

In general, the adsorption is always accompanied by a thermal process (Rytwo and Ruiz-Hitzky 2003; Ramesh et al. 2005) which may be either exothermic (ΔH° < 0) or endothermic (ΔH° > 0). Measuring the heat of adsorption ΔH° is the main criterion that differentiates the chemisorption of physisorption.

The heat of adsorption ΔH° is given by the Gibbs–Helmholtz relationship (El-Rahman et al. 2006; Demirbas et al. 2006):

$$\Delta G{^\circ} = -\, \text{RT}\ln K_{\text{c}}$$
(14)
$$\Delta G{^\circ} = \Delta H{^\circ } - T\Delta S{^\circ }$$
(15)
$$\frac{{\left( {14} \right)}}{{\left( {15} \right)}}\;{\text{Ln}}K_{\text{c}} = \frac{{\Delta S{^\circ }}}{R} - \varvec{ }\frac{{\Delta H{^\circ }}}{R \cdot T}$$
$$\text{With}: K_{\text{c}} = \frac{{C_{\text{e}} }}{{M \cdot \text{(}C_{\text{0}} - C_{\text{e}} \text{)}}} \cdot V$$

where: K c equilibrium constant, ΔG° Gibbs free energy (J mol−1), ΔH° enthalpy (KJ mol−1), ΔS° entropy (KJ mol−1 K−1), T absolute temperature (K), C o initial concentration of the adsorbate, C e equilibrium concentration of the adsorbate, V volume of solution, m mass of the sorbent, R gas constant (8.314 J mol−1 K−1).

The heat of adsorption ΔH° and the entropy ΔS° adsorption on clay was determined graphically by plotting LnK c in function of the inverse of the temperature in Kelvin of the medium as shown in Fig. 14.

Fig. 14
figure 14

Determination of the enthalpies and entropies of adsorption of pharmaceuticals onto clay

Full size image

The positive value of ΔH° (11.06 kJ mol−1) confirms that the adsorption of adsorbate on the clay is an endothermic process. Also, the low values of this heat (<40 kJ mol−1) indicate that this is a physical adsorption. The positive value of ΔS° (0.03 kJ mol−1 K−1) corresponds to an increase in randomness at the solid solution interface with some structural changes in the adsorbate and adsorbent (Kyzas and Koltsakidou 2015). Also, some structural changes may have taken place as a result of interaction of molecule with active groups in the clay surface (Yadava et al. 1991).

The negative values of ΔG° of drugs onto clay at different temperatures explain the spontaneous nature of the sorption process

Conclusion

This study indicates that the clay which contains a mixture of (smectite-kaolinite) and quartz could be used as an efficient low-cost adsorbent. Kinetic data of pharmaceuticals followed the pseudo-second-order kinetic model. Langmuir and Freundlich equations were used to describe the adsorption of drugs onto clay. The Freundlich equation is in good agreement with the experimental results. The adsorption isotherms pharmaceuticals of clay are satisfactorily described by the Freundlich model. The positive values of ΔH° confirm the endothermic nature of the adsorption. The increasing values of ΔG° with temperature show the spontaneity in the sorption processes pharmaceuticals reagent on clay.