Introduction

Drinking arsenic-contaminated water leads to a series of health problems. Arsenic is a toxic metalloid element that is now recognized to be an important contaminant in drinking water in many countries of south-East Asia including Bangladesh (Sohel et al. 2009), Pakistan (Islam-ul-haq et al. 2007), China (Li et al. 2011), etc. The effects of arsenic are not immediately visible as people can absorb significant quantities of arsenic without any immediate health complications. Treatments are required to remove arsenic and provide treated water for consumption. Some cost effective filtration systems have been developed in past but the main problem is that the socio-economic conditions of the effected people do not allow use of these filters easily in developing countries. There is need to provide low cost technique for removal of arsenic so that safe water is provided at consumer’s end (António et al. 2009).

Drinking water is now recognized as a major source of human intake of arsenic in its most toxic (inorganic) form (Dinesh et al. 2007 ). Arsenic is found in natural environment and behaves as a metalloid. It can exist in organic and inorganic (i.e., most toxic) forms. About one-third of the arsenic in the atmosphere comes from high temperature natural processes, such as coal-fired power plants, burning vegetation and volcanic activity. Rest comes from human activities. Due to natural geological contamination, high levels of inorganic arsenic can be found in drinking water that has come from deep drilled wells (Bundschuh et al. 2011). This is particularly true for Bangladesh, India and Taiwan (Garelick et al. 2005).

In 2010, the World health organization (WHO) estimates that due to long-term arsenic exposure, thousands of people from Pakistan to Vietnam died of cancer each year. Cardiovascular disease and mental development of children are also caused by arsenic (Scott et al. 2010). In the light of potency of arsenic, United States Environmental protection agency (US-EPA) concluded that arsenic is Group A carcinogen, known to trigger skin, bladder, and lung cancers and thus has become a metaphor for poison. Hundreds of millions of people daily use drinking water with arsenic concentrations several times higher than the World Health Organization (WHO) recommended limit of 10 millionths of a gram per liter of water (10 µg/L) (Garelick et al. 2005; Moffat et al. 2014).

The predominant forms of As in water supplies mostly are inorganic species arsenate [As(V)] and arsenite [As(III)]. Arsenic is exclusively sensitive to mobilization (pH 6.5–8.5) and exists under both oxidizing and reducing conditions among heavy metalloids. The As(V) species are mostly stable in oxygen-rich environment and exist as oxyanions (H2AsO4 − and HAsO4 2−) at neutral pH, whereas As(III) species predominant in moderately reducing anaerobic conditions exist as H3AsO3 at neutral pH. As(III) is more toxic and more difficult to remove with the conventionally applied physiochemical treatment methods than As(V) (Dinesh et al. 2007).

A large number of remediation technologies for arsenic removal have been developed, but mostly are available for central water treatment plants at industrial level. However, options for local treatment of water are not fully developed. The available methods include arsenic removal by ion exchange, removal by filtration and precipitation/co-precipitation, coagulation/electro coagulation, removal by adsorption onto artificial and natural sorbents, water softening with lime, membrane processes and bioremediation (António et al. 2009; Dinesh et al. 2007; Dhiraj et al. 2008). These technologies mostly have cost issue and are greatly used for heavy metal removal from wastewater (Dinesh et al. 2007). Many researchers have tried to use naturally occurring materials as low cost adsorbents for removing heavy metals. The metal adsorption capacities of adsorbents depend upon different factors such as concentration of metal ions, pH, contact time and characteristics of individual adsorbent. One of the cost effective and highly efficient sources for adsorption technology is waste of agriculture (Roya et al. 2013). Studies reveal that a variety of agricultural waste materials such as wheat bran, wheat husk (Roya et al. 2013), bark of the trees, coconut shells, ground net shell, walnut shells, tea waste (Dhiraj et al. 2008), coffee beans (Boonamnuayvitaya et al. 2004), maize corn cob (Sekhula et al. 2012), sugar cane bagasse, apple, banana, orange peels (Annadurai et al. 2003), soya bean hulls, sugar beet pulp, sunflower stalks (Hashem et al. 2007), cotton stalks, etc. have been tried to remove metal ions either in their natural form or after some physical or chemical modification (Dinesh et al. 2007). However, a very few studies were done on raw rice husk (Nurul Amin et al. 2006) as a remediation material for removal of arsenic from groundwater.

The purpose of the present work is to explore the potential of raw rice husk as adsorbent in a fixed bed column as well as batch studies for removing As(V) from drinking water. Rice husk is available easily at no or very low cost as agro waste. Moreover, the effect of various parameters such as flow rate, adsorbent volume, and diameter of column, particle size of adsorbent and initial metal concentration on the removal of arsenic was investigated to reveal the performance of column.

Materials and methods

Reagents adsorbent preparation

The reagents that have been used in the present study were of analytical grade and used to make calibration standards. Stock solutions (1000 μg/L) of As(V) were prepared in distilled water from solid KH2AsO4. Rice husk was the adsorbent used for the removal of arsenic ions from their aqueous solution. Rice husk was taken from a local market. Then, it was ground and sieved to a size of 1.18 mm (No# 16), 850 µm (No# 20) and 710 µm (No# 25) to have uniform size of adsorbent. Three different sizes were used to study the effect of particle size of rice husk on removal efficiency of arsenic, whereas to study the effect of other parameters such as flow rate, initial arsenic concentration feed and bed height, only one of the sizes (i.e., 1.1 mm No# 16) was used. The adsorbent was then washed with deionized water and dried in an oven at 100 °C for 48 min to remove moisture contents. After that, adsorbent was stored in air tight jars for further use.

Fixed bed column setup

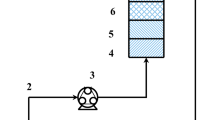
The continuous flow adsorption experiments were conducted using glass columns of 2.5 and 5 cm inside diameter and height of 1.5 m. In the lower end of the column, a 0.5 mm sieve was used to adjust the required height of the adsorbent media (rice husk) and to support the adsorbent in the column. To adjust the height of rice husk, a wire is fixed with the sieve that allows the sieve to move in the column. A peristaltic pump was used for injecting As(V) solutions to the top of the column from the feed tank. It has a capacity of pumping liquids from 2 to 25 mL/min at different pressures. The flow rate can be controlled or adjusted with the help of flow meter as shown in Fig. 1.

Fig. 1
figure 1

Schematic diagram of the experimental setup for fixed bed column adsorption

Full size image

Analytical procedure

Flow was directed downward as feed (initial arsenic solution) was applied from the top. Continuous study was carried out to determine the effect of different operating parameters like flow rate, height of adsorbent bed, effect of column diameter, initial metal concentration dose and effect of particle sizes of adsorbent. Pre-weighed amount of adsorbent was filled in column. It was air tighten with the help of screws present at inlet of the column so that water must flow under pressure. At the required flow rate, metal solution of known concentration was fed from the feed tank with the help of peristaltic pump. Effluent samples were collected at different time intervals to achieve exhaust time (The time at which adsorbent get saturated and the time at which adsorbent has maximum capacity to absorb the metal). Then, samples were analyzed for their absorbance using atomic adsorption spectrophotometer (AAS).

Removal efficiency of metal ions was calculated using the following Eq. (1)

$$ {\text{Removal Efficiency }}\left( {\text{R.E}} \right) \, \% \; = \;\frac{{C_{\text{o}} - C}}{{C_{\text{o}} }}\; \times \;100 $$
(1)

whereas C 0 and C are the concentrations of As in sample water before and after the treatment, respectively.

Experimental study results

Effect of column diameter and bed height

As shown in Fig. 2, different removal efficiencies were achieved at different diameter columns, i.e., 5 cm and 2.5 cm for the fixed adsorbent quantity of rice husk (47.5 g) and influent metal concentration of 15 ppb by keeping the flow rate constant (7 mL/min). The whole experiment was repeated for the influent metal concentrations of 30 ppb and 50 ppb. It was observed that the maximum average removal of 80.7 % was achieved in 5 cm diameter column at bed height of 28 cm with 47.5 g adsorbent quantity. The reason is that larger diameter with greater column depth increased the contact between metal solution and adsorbents, allowing metal ions to better adsorbed at available binding sites of the adsorbents.

Fig. 2
figure 2

Effect of diameter on removal efficiency at 7 mL/min in 2.5 and 5 cm diameter columns

Full size image

The effect of bed height on the continuous column adsorption can also be determined using the time to reach breakthrough point and the shape of the breakthrough curve as shown in Fig. 3. An increase in bed height resulted in more contact time being available for As(V) to interact with the rice husk (Palas et al. 2013). This phenomenon has allowed As(V) to diffuse deeper into the rice husk. Subsequently, the percentage of arsenic removal increased when the bed height was increased.

Fig. 3
figure 3

Breakthrough curve showing the effect of bed height in 5 cm column at 7 mL/min for ppb As(V) concentration

Full size image

Effect of flow rate

The adsorption behavior of rice husk was investigated by altering the flow rate in the range of 7 to 20 mL/min. The breakthrough curves obtained by keeping constant the metal concentration of 15 ppb at bed height of 28 cm in 5 cm diameter column are shown in Fig. 4. It was observed that quicker breakthrough was achieved for higher flow rates of As(V) solution. The reason is that at low flow rate, rice husk takes more time to achieve saturation. This can be explained by the fact that at higher flow rates, the residence time of the adsorbate in the column would decrease but at lower flow rates metal ions have more time to diffuse into the pores of adsorbent through intra-particle diffusion. Conversely, for the higher flow rate, the arsenic solution will leave the column bed before the equilibrium can be reached. Nurul-Amin et al. (2006) reported the same trend that removal efficiency for As(V) decreased as the treatment flow rate was increased.

Fig. 4
figure 4

Breakthrough curve showing the effect of flow rate in 5 cm column for 15 ppb arsenic concentration

Full size image

Effect of initial metal concentration

The effect of initial metal concentration was investigated on column by altering influent concentrations of 15, 30, 50 and 70 ppb. The bed height, diameter of the column and flow rate were kept constant at 28 cm (47.5 g rice husk), 5 cm and 7 mL/min, respectively, as shown in Fig. 5. It was revealed that the treated volume was higher at low concentration. However, the adsorption capacity increased with increasing the initial As(V) concentration (ppb) due to a raise in the driving force of the concentration gradient. At low influent concentration, the driving force of adsorbent was reduced due to low concentration gradient. It is also evident from the breakthrough curve Fig. 5 that maximum removal was 15 ppb and minimum removal was 70 ppb. The slow transport of As(V) onto rice husk column was due to the lower concentration gradient and resulted in a slower breakthrough curve. Conversely, a higher concentration of As(V) has been shown to lead to a higher driving force for the As(V) ions to overcome the mass transfer resistance in the liquid phase. Consequently, quick saturation of the available binding sites for rice husk has caused the breakthrough time to decrease with the increasing inlet As(V) concentration (Palas et al. 2013).

Fig. 5
figure 5

Breakthrough curve showing the effect of feed concentration in 5 cm column at bed height of a 28 cm at 7 mL/min for 15, 30, 50 and 70 ppb As(V) concentration

Full size image

Effect of particle size

The effect of particle sizes was observed in column adsorption by varying sizes of 1.18 mm (16 mesh), 850 µm (20 mesh) and 710 µm (25 mesh). For 15 ppb initial influent concentration, experiment was conducted at a flow rate of 7 mL/min in 5 cm column at bed height of 28 cm as shown in Fig. 6. It was concluded that by reducing the particle size of rice husk, removal efficiency increased from 7 to 20 %. This might be due to the fact that by increasing the surface area of particles and compaction between the particles, removal efficiency increased. The more the binding sites available, the more efficient will be the adsorption process (Neeta and Jatinder 2008). Likewise, breakthrough curves showing the same effect of particle sizes for 70 ppb As(V) concentration under the same operating conditions are illustrated in Fig. 7.

Fig. 6
figure 6

Removal efficiency showing the effect of particle sizes in 5 cm column at bed height of a 28 cm at 7 mL/min for 15 ppb As(V) concentration

Full size image
Fig. 7
figure 7

Breakthrough curve showing the effect of particle size in 5 cm column at bed height of 28 cm for 70 ppb As(V) concentration at 7 mL/min

Full size image

Effect of pH

pH is one of the most vital parameters controlling the metal ion sorption process. Figure 8 depicts the effect of pH on As(V) removal with removal efficiency. The removal efficiency of As(V) increased slightly with increasing pH, was nearly constant above pH 8, and decreased tremendously at pH > 12. For the removal of As(V), the efficiency curve was basically a plateau in the pH range of 8–10, and then the efficiency leaned to decrease with increasing pH. The poor As(V) removal efficiencies at high pH can be attributed to the following reasons: Essentially, chemical species for As(V) in this pH region is oxy-anions. Moreover, hydroxyl groups are more abundant on the surface of rice husk with increasing pH. Hence, the maximum removal was achieved at pH 8. Nurul-Amin et al. (2006) also reported that maximum removal for As(V) was observed in comparative neutral region, i.e., 8.

Fig. 8
figure 8

Removal efficiency showing the effect of pH in 5 cm column at 7 mL/min for 15 ppb As(V) concentration

Full size image

Quantitative analysis discussion

Adsorption isotherms

Langmuir isotherm

The Langmuir’s isotherm model is given by the following Eq. 2 (Hameed et al. 2007):

$$ \frac{{C_{e} }}{{q_{e} }}\; = \;\frac{1}{{Q_{\text{o}} b}}\; + \;C_{e} \frac{1 }{{Q_{\text{o}} }} $$
(2)

where C e is the equilibrium concentration of the adsorbate (µg/L), q e is the amount of adsorbate adsorbed per unit mass of adsorbate (µg g−1), and Q o and b are Langmuir constants rated to adsorption capacity and rate of adsorption, respectively. When C e /q e was plotted against C e, straight line with slope 1/Q o was obtained as shown in Fig. 9, indicating that the adsorption of As(V) on rice husk follows the Langmuir isotherm. The Langmuir constants ‘b’ and ‘Q o’ were calculated from this isotherm and their values are given in Table 1.

Fig. 9
figure 9

Langmuir adsorption isotherm of arsenic-rice husk adsorption at room temperature (25 °C)

Full size image
Table 1 Langmuir and Freundlich isotherm constants for arsenic
Full size table

The important characteristics of the Langmuir isotherm can be expressed as dimensionless equilibrium parameter (R L) which is defined by Eq. (3) (Hameed et al. 2007):

$$ R_{{{\text{L}}\;}} \; = \;\frac{1}{{1 + b C_{\text{o}} }} $$
(3)

where b is the Langmuir constant and C 0 is the maximum arsenic concentration (µg L−1). The value of R L is indicator showing the type of the isotherm to be favorable (0 < R L < 1), linear (R L = 1), unfavorable (R L > 1) or irreversible (R L = 0). Value of R was found to be 0.84 and confirmed that the rice husk is favorable for adsorption of arsenic under conditions used in this study.

Freundlich isotherm

The logarithmic form of Freundlich model is expressed as the following Eq. (4) (Hameed et al. 2007):

$$ { \log }\,q_{\text{e}} = { \log }\,\;K_{\text{F}} + \, \left( { 1/n} \right)\;\,{ \log }\,C_{\text{e}} $$
(4)

where q e is the amount adsorbed at equilibrium (µg g−1), C e is the equilibrium concentration of the adsorbate and K F and n are Freundlich constants, n value showing how favorable the adsorption process and K F [mg g−1(l mg−1)n] is the adsorption capacity of the adsorbent. K F represents the quantity of As(V) adsorbed onto rice husk adsorbent for a unit equilibrium concentration. The slope 1/n ranging between 0 and 1 is a measure of adsorption intensity or surface heterogeneity. A value for 1/n < 1 indicates a normal Langmuir isotherm while 1/n > 1 is indicative of cooperative adsorption. The plot of log q e versus log C e gives straight lines with slope ‘1/n’ (Fig. 10), which shows that the adsorption of arsenic also follows the Freundlich isotherm. The value of 1/n obtained was 0.344, which indicates favorable adsorption. K F and n were calculated and recorded in Table 1.

Fig. 10
figure 10

Freundlich adsorption isotherm of arsenic-rice husk adsorption at room temperature (25 °C)

Full size image

Kinetic models

Adam-Bohart model

The following expression was used to find out the saturated concentration of adsorbate (Zhao et al. 2011):

$$ \frac{Ct}{Co}\; = \;{ \exp }\left( {K_{\text{AB}} Co \, t{-}K_{\text{AB}} N_{\text{o}} \frac{Z }{F}} \right) $$
(5)

where K AB is the kinetic constant (L/µg.min), F is the linear velocity (cm/min) that is the ratio of flow (mL/min) and cross sectional area (cm2), N o is the saturation concentration (µg/L), Z is the bed depth of column (cm) and t is the time (min). K AB and N o were the parameters used to describe the characteristic operations of the column. \( {\text{Ln}}\;\left( {\frac{Ct}{Co}} \right) \) was plotted against time (t) using linear regression. K AB and N o values were determined from the intercept and slope of the graph. Table 2 shows the values of kinetic constants and saturated concentrations calculated using Adam-Bohart model at different bed heights, flow rates and inlet feed concentrations in 5 cm diameter column.

Table 2 Adam-Bohart constants for 5 cm diameter column at different bed heights and flow rate
Full size table

It is shown from the Table 1 that correlation coefficient R 2 was in the range of 0.733 to 0.959 for 15, 30, 50 and 70 ppb inlet arsenic concentrations. The results indicate that N o had no definite pattern when the inlet As(V) concentration, flow rate and bed height were increased. The kAB values decreased from 0.00135 to 0.000461 mL/min.µg when the inlet As(V) concentrations increased from 15 to 70 ppb, whereas it increased from 0.00135 to 0.00179 when the flow rate increased from 7 mL/min to 20 mL/min. Hence, it can be concluded that the overall kinetics in the initial part of the adsorption process were dominated by external mass transfer.

Thomas Model

The following expression was used to find out the maximum adsorption capacity of rice husk (Palas et al. 2013):

$$ \frac{{C_{t} }}{{C_{\text{o}} }}\; = \;\frac{1}{{1 + \exp ( {\text{KTH}} q_{\text{o}} \frac{m }{Q} - {\text{KTH}} C_{\text{o}} t)}} $$
(6)

where q o is the equilibrium As uptake per g of the rice husk adsorbent (µg/g), m is mass of the rice husk in grams (g), Q is the flow rate (mL/min), K TH is the Thomas rate constant (L/µg.min), C o is the initial metal concentration (ppb) and Ct is the effluent metal concentration (ppb). The values of K TH and q o were determined from a plot of \( {\text{Ln}} \left( {\frac{{C_{0} }}{Ct }\;\; - \;\,1} \right) \) against time (t) using linear regression analysis. Table 3 presents calculated values of kinetic constants and uptake capacity of arsenic at different flow rates, bed heights and inlet feed concentrations of arsenic in 5 cm diameter column.

Table 3 Thomas model constants for 5 cm diameter column at different bed heights
Full size table

It can be seen from the Table 3 that all the factors (the inlet arsenic concentration, flow rate and bed height) affect the Thomas rate constant (k TH) and the equilibrium of arsenic uptake (q o). The inlet arsenic concentration and bed height influence the k TH and q 0 in a similar pattern. When the inlet As(V) concentration increased from 15 to 70 ppb, the k TH decreased from 0.00235 to 0.000699 mL/min µg while the qe increased from 103.6 to 416.7 µg/g. Whereas, when the bed height increased from 15 to 28 cm, the k TH decreased from 0.00647 to 0.00235 mL/min µg and the q o increased from 50 to 103.6 µg/g. These findings could be attributed to the higher driving force of the higher inlet As(V) concentration (Padmesh et al. 2005). The R 2 values were in the range of 0.768 to 0.964.

Yoon and Nelson model

Yoon and Nelson model was based on the assumption that the rate of decrease in the probability of adsorption of adsorbate molecule is proportional to the probability of the adsorbate adsorption and the adsorbate breakthrough on the adsorbent. The following expression was used (Zahra et al. 2013)

$$ {\text{Ln}}\;\frac{Ct}{{C_{\text{o}} - Ct}} \; = \;\;K_{{_{\text{YN}} }} t \, - \, K_{{_{\text{YN}} }} {\rm T} $$
(7)

where K YN (1/min) is the rate velocity constant. T (min) is the time required for 50 % adsorbate breakthrough. K YN and T were determined from intercept and slope from the linear plot of \( {\text{Ln}}\;\frac{Ct}{{C_{\text{o}} - Ct}} \) against sampling time (t). Table 4 represents calculated values of rate velocity constants and time required for 50 % adsorbate breakthrough, using Yoon and Nelson model at different flow rates, bed heights and inlet feed concentrations in 5 cm diameter column.

Table 4 Yoon and Nelson model constants for 5 cm diameter column at different bed heights and flow rate
Full size table

The results indicate that the k YN value increased from 0.0235 to 0.0489 L/min when inlet As(V) value increased from 15 to 70 ppb. This was due to the fact that by increasing the initial arsenic concentration competition between the adsorbate molecules for the binding sites increased and ultimately resulted in the increased uptake capacity of rice husk. Rate constant (K YN ) increased with increase in flow rate, whereas “T” decreased with decreasing bed height. The linear regression coefficient (R 2) was in the range of 0.7954–0.9641.

Disposal method for rice husk

Once the rice husk become exhausted, the problem of how to dispose of concentrated arsenic product must be addressed. Regeneration of rice husk is not cost effective and recovery of arsenic has limited markets (Verma et al. 2014). One attractive option for treating rice husk is encapsulation through solidification followed by disposal of treated landfills ((Leist et al. 2003). To form satisfactory storable solids, several solidification attempts were made based on literature studies; thus, in this study the effective solidification was done through arsenic concentrates incorporated into Portland cement.

Conclusions

The proposed fixed bed column treatment system is appropriate and suitable domestic approach to arsenic removal in local areas, because of its simplicity, easy operation and handling. The present method is effective for a wide range of arsenic concentrations (i.e., 15–70 ppb), which is quite similar to those observed in contaminated groundwater of south Asian countries. Adsorption isotherm study was carried out on two well-known isotherms models, Langmuir and Freundlich. Langmuir model yielded a somewhat better fit (R 2 = 0.986) than the Freundlich model (R 2 = 0.948). Column operations under different conditions were also employed to study its practical applicability of rice husk in the removal of arsenic. The column experimental data were fitted well to the Adam Bohrat, Thomas and Yoon–Nelson models for arsenic feed concentrations from 15 to 30 ppb at the flow rate of 7 mL/min. No secondary-pollution problem will occur, because solidification of the arsenic is possible through arsenic concentrates incorporated into Portland cement. Moreover, it has recycling potential and can be used as cement/insulation panels and roof sheets.