1 Introduction

Egypt entered a new era of mega-national projects, the economic sector witnessed a qualitative leap in various sectors, which formed the backbone of development in the Egyptian economy. The development process has begun in all fields and many achievements have been made under his instructions including 14,762 projects in various sectors that have been completed at an estimated cost of 2207.3 billion (Efforts-Economic-Development-in-8-Years, n.d.). The contract plays an important role in building projects, Contract management, contractor selection, and optimization of contract management are all crucial to the successful completion of any project (Russell et al. 1999). Any hiccups in the bidding process throughout contract management might lead to complications in the final delivery of the project (Miller et al. 2002; Thompson Richard and Lucko 2012). Tendering is a complicated and costly procedure for public entities, particularly in the construction sector. Therefore, choosing a construction contractor is one of the most important decisions that may affect the progress and accomplishment of any building project. The primary goals of the contractor selection process are decreasing project risk management, maximizing quality, and maintaining good connections among project stakeholders (Chapman 2001; Singh and Tiong 2005). Traditionally, the lowest tender price is sometimes considered the most significant factor in the contractor selection process (Alirezaie and Razavi Khosroshahi 2014; Russell and Skibniewski 1988; Wong et al. 2000). For example, contractors' selection for public projects has been centered on the premise of accepting the lowest offer price. Therefore, the wrong selection of the contractor based on the lowest tender price concept could lead to delays and a lack of quality in these projects because contractors urgently offered the lowest tender price to stay in business (Singh and Tiong 2006; Holt et al. 1994).

The wrong selection of contractors for projects can have significant adverse effects on project outcomes. In many construction projects, choosing contractors based on their lowest bid price is a typical practice. The lowest bidder may seem like the best option, but this strategy has its own set of issues and difficulties. The following are some problems with choosing contractors purely based on the lowest bidding price:

  1. 1.

    Poor Quality Work: Choosing a contractor who lacks the necessary expertise, experience, or resources can result in subpar work quality. This can lead to rework, delays, and compromised project deliverables, negatively impacting the overall project success.

  2. 2.

    Cost Overruns: Inadequate contractor selection can contribute to cost overruns. Contractors who are unable to accurately estimate project costs, manage resources efficiently, or adhere to budget constraints can cause financial strain on the project. Unanticipated expenses and delays can accumulate, leading to budget overruns.

  3. 3.

    Schedule Delays: Contractors who are not well-suited for the project may face difficulties in meeting project timelines and milestones. Delays in project execution can disrupt the entire project schedule, affecting subsequent activities and potentially resulting in missed deadlines and contractual penalties.

  4. 4.

    Safety Risks: Inappropriate contractor selection can pose safety risks on the project site. Contractors with inadequate safety protocols, training, or compliance measures may increase the likelihood of accidents, injuries, and potential legal liabilities. This not only compromises worker safety but also leads to project disruptions and reputational damage (Bahootoroody et al. 2021).

  5. 5.

    Disputes and Contractual Issues: Selecting contractors without conducting proper due diligence can result in contractual disputes and conflicts. Contractors who fail to meet their contractual obligations or deliver as per the agreed terms can lead to legal disputes and prolonged resolution processes, causing project delays and additional costs.

  6. 6.

    Damaged Stakeholder Relationships: Wrong contractor selection can strain relationships with project stakeholders, including clients, investors, and subcontractors. Poor performance, delays, and quality issues can erode trust and confidence in the project, potentially affecting future collaborations and business opportunities.

  7. 7.

    Reputational Damage: The selection of underperforming contractors can harm the reputation of the project owner or organization. Negative project outcomes, financial losses, and project failures can impact the perception of stakeholders and the organization's credibility within the industry, making it more challenging to secure future projects. A similar technique is used in the selection of subcontractors (Demirkesen and Bayhan 2019).

The challenge of contractor selection depends on choosing a contractor who can take on the client's project and complete it well to satisfy the client's schedule, cost, and quality requirements (Hatush and Skitmore 1998). On the other hand, contractor prequalification considers and assesses several criteria such as tender price, accomplishment time, technical capability experience, management capability, safety, and economic status to select the optimum contractor from among the candidates (Aladağ and Işik 2018; Gurgun and Koc 2020; Keshavarz-Ghorabaee et al. 2018; Whitney 2003; Zhang 2020). As a result, one essential issue in contractor selection that affects project outcomes is the choice of selected criteria (Ling 2004; Best and Langston 2006). The selection of a single contractor is an area where researchers and specialists have made substantial contributions to the enhancement of contractor selection (Alirezaie and Razavi Khosroshahi 2014; El-Abbasy et al. 2013; Kumaraswamy and Walker 2021; Safa et al. 2015).

Several frameworks were developed to select a suitable contractor for a construction project. These frameworks can be divided into two main categories: empirical and mathematical frameworks. First, the empirical framework examines actual contractor selection processes in practice. For example, they conducted a study of contractor selection practices in Saudi Arabia and found that cost was the most important factor considered when selecting contractors. Similarly, they conducted a study of contractor selection practices in Qatar and found that past performance was the most important factor considered when selecting contractors. Second, the mathematical framework focuses on developing models or frameworks for selecting contractors based on criteria such as cost, quality, and risk. For example, they developed a multi-criteria decision-making model for selecting contractors based on cost, quality, and risk factors. Similarly, they developed a framework for selecting contractors based on criteria such as technical capability, financial capability, and past performance. The multi-criteria decision-making (MCDM) approach may solve a wide set of management issues that have several aspects linked to it (Antoniou and Aretoulis 2019).

Parameters are sometimes known as "goals" or "decision criteria". Parameters are many aspects through which the options might be shown (Bona et al. 2020). Road maintenance contractor selection is a critical decision-making process that requires careful evaluation of several criteria. An efficient method that may be used to assess and choose the best contractors for road maintenance projects is multi-criteria decision-making (MCDM). MCDM enables decision-makers to methodically evaluate and contrast several factors to reach well-informed conclusions (Agarwal et al. 2023). The following is a thorough description of how MCDM may be used to choose contractors for road maintenance:

  1. 1.

    Establish the Criteria: The first stage is to establish the standards by which the contractors will be judged. These standards should apply to road upkeep and may include elements like experience, skill, cost, quality, punctuality, safety record, environmental practices, and resource accessibility.

  2. 2.

    Define the Weights: After the criteria have been determined, decision-makers must give each criterion a weight to represent its relative significance. Expert judgment, surveys, and analytical approaches like the Analytic Hierarchy Process (AHP) or the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) may all be used to calculate the weights.

  3. 3.

    Create an Evaluation Scale: A scale must be created to rank the contractors' accomplishments about each requirement. Depending on the criteria, this might be a quantitative or qualitative scale. One way to grade experience is on a scale of 1–5, where 1 is the lowest and 5 is the greatest.

  4. 4.

    Collect Information: Information gathering is required to assess how well the contractors performed against each criteria. This may be achieved using a variety of techniques, including looking through the records of their previous projects, conducting interviews, asking for bids, and contacting references.

  5. 5.

    Assess each contractor's performance about each criteria using the defined assessment scale. Using the information gathered, assign scores or ratings.

  6. 6.

    Normalize the Data: Since the criterion may utilize many scales or measurement units, it is crucial to normalize the data to remove any bias brought on by the various measurement scales. This may be accomplished by converting the scores into a standard scale, such as one with a 0–1 scale.

  7. 7.

    To get weighted scores, multiply the normalized scores by the weights that were applied to each criteria. In this phase, the criteria with higher weights are given more consideration, enabling a thorough assessment of the contractors.

  8. 8.

    Calculate an overall score by adding the weighted scores for each contractor. Taking into account all the examined factors, this score represents the contractor's suitability for the road repair project.

  9. 9.

    Sensitivity Analysis: Conduct sensitivity analysis to evaluate how reliable the findings are. To do this, the weights given to each criteria must be slightly modified to reevaluate the contractors. It aids in comprehending how shifting priorities affect the choices made in the end.

  10. 10.

    Rank the contractors from top to lowest based on the combined ratings and the findings of the sensitivity analysis. The contractor chosen for the job of maintaining the roads is the one that received the highest score. Before making a final selection, it is crucial to take into account other considerations including financial limitations, contract conditions, and legal obligations.

Decision support systems are automated decision-making systems that can assist decision-makers in circumstances involving a large quantity of data (Agarwal et al. 2022). Evidential reasoning employs the idea of the degree of belief in situations with ambiguous and/or partial information to ensure that a reasonable decision may be reached based on the decision maker's true preferences. Deviation variables with specified priorities and weights are reduced to achieve the highest priority goal according to two methods TOPSIS and VIKOR. Firstly, TOPSIS is an abbreviation of the Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) is a multi-criteria decision-making (MCDM) method that is used to evaluate the relative closeness of a set of alternatives to an ideal solution (Gyani et al. 2022). It was developed by Yoon and Hwang in 1981 with additional advancements by Yoon in 1987 and Hwang, Lai, and Liu in 1993, Zavadskas presented a strategy for selecting contractors for building projects using TOPSIS methodologies (Horton and Eaton 2017; Jabbarzadeh 2018; Di Bona et al. 2019).

That has since been widely used in many different fields, including engineering, economics, finance, and operations research. The TOPSIS method is based on the concept of “distance” between alternatives and an ideal solution. The distance between two points is calculated using a distance measure such as Euclidean or Manhattan distance. The alternative with the shortest distance from the ideal solution is then selected as the best option Gul et al. (2016), Holt et al. (1994), Miller et al. (2002).

Several studies utilized TOPSIS in various applications. For example, Yang et al. (2009) used TOPSIS to choose an appropriate container transport mode to prevent delivery delay (Yang et al. 2009). Kumar and Singh (2016) utilized the TOPSIS Algorithm to optimize the cutting settings to improve the surface finish of Titanium alloy during face milling (Kumar and Singh 2016; Bognár et al. 2022; Irfan et al. 2022). Also, TOPSIS has been used to evaluate supplier selection decisions in supply chain management (SCM), prioritize projects in project management (PM), and select investments in financial portfolio management (FPM).

In addition, researchers have proposed various modifications to improve the performance of TOPSIS such as incorporating fuzzy logic into the decision process and using different weighting schemes for criteria evaluation. For example, Yong (2006) used fuzzy TOPSIS to select a location to build a new plant (Yong 2006). TOPSIS is considered a popular choice among researchers looking for an effective way to compare multiple alternatives simultaneously due to: (1) simple and straightforward method for multi-criteria decision making; (2) it is easy to understand and implement; (3) it takes into account both qualitative and quantitative criteria; (4) it allows for the inclusion of multiple criteria in the decision-making process; (5) it can be used to rank alternatives based on their relative closeness to an ideal solution; (6) it can be used to compare alternatives with different scales of measurement (e.g., nominal, ordinal, interval, or ratio); (7) the results are easy to interpret and explain to stakeholders involved in the decision-making process; (8)the method is suitable for both small and large problems with multiple criteria and alternatives (Behzadian et al. 2012).

Secondly, the VIKOR method has been applied to a variety of decision-making problems, including resource allocation, project selection, supplier selection, and portfolio optimization. The VIKOR technique is based on a specific measure of proximity to the positive ideal solution. As a result, the VIKOR technique is appropriate for scenarios in which the decision maker seeks to maximize profit while minimizing risk is less significant (Javidi et al. 2022).

The Vikor method is based on two main concepts: the relative importance of each criterion and the relative performance of each alternative concerning each criterion.

These scores are then used to calculate an overall score for each alternative, which can be used to rank them according to their overall performance (Gul et al. 2016). For example; Vučijak et al. (2013), used VIKOR for evaluating sustainable hydropower (Vučijak et al. 2013), and Quijano et al (2012), used VIKOR for the development of renewable sustainable energy plans (Quijano et al. 2012). Finally, it provides an objective way of ranking alternatives that takes into account both individual preferences and collective objectives as follows (Mardani et al. 2016); (1) The Vikor method is a multi-criteria decision-making technique that allows for the evaluation of multiple criteria simultaneously; (2) it is a simple and easy to use a method that can be applied to a wide range of decision-making problems; (3) it provides a systematic approach to decision making, which can help reduce the risk of bias in the decision-making process; (4) the method is relatively easy to understand and implement, and it can be used by both experts and non-experts alike. Both TOPSIS and VIKOR methodologies have been extensively applied in various industries and decision-making contexts, and they have proven to be effective in handling complex decision problems with multiple criteria. By utilizing these methodologies for contractor selection in Egyptian road maintenance, stakeholders can make informed decisions based on a comprehensive evaluation of contractors' performance across various criteria, leading to more reliable and objective contractor selection processes (Agarwal et al. 2023; Darbari et al. 2019; Di Bona et al. 2019).

This paper integrates both methods TOPSIS and VIKOR to magnify their capabilities and overcome their limitation.

Several models were developed to consider contractor prequalification criteria based on two techniques of a multi-criteria decision-making strategy to provide the optimum selection of the contractor/s for the construction projects. The integration of TOPSIS, VIKOR, and AHP into a single model can be beneficial for multi-criteria decision-making. It offers a more comprehensive evaluation and flexibility in decision-making. However, decision-makers should be cautious about the complexity, subjectivity, data requirements, and computational burden associated with this integrated model. Additionally, the model may require additional techniques to explicitly address uncertainty in the decision-making process.

2 Methodology

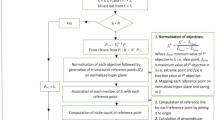
This paper presents the multi-criteria decision-making algorithms that integrate AHP with TOPSIS and VIKOR in the selection of optimum contractors for construction projects as shown in Fig. 1.

Fig. 1
figure 1

Show Topsis and Vikor analysis for contractor selection

Full size image

The TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution) and VIKOR (Vise Kriterijumska Optimizacija I Kompromisno Resenje) methodologies were chosen for contractor selection in Egyptian road maintenance due to their effectiveness in handling multiple criteria and providing comprehensive decision-making frameworks as follows:

  1. 1.

    TOPSIS: Is a widely used multi-criteria decision-making method that considers both positive and negative aspects of alternatives. It calculates the relative closeness of each alternative to the ideal solution by evaluating the distances between the positive ideal solution and the negative ideal solution. In the context of contractor selection, TOPSIS can effectively assess contractors based on various criteria (e.g., experience, cost, quality, time) and rank them according to their proximity to the ideal contractor.

  2. 2.

    VIKOR: Is another multi-criteria decision-making method that is suitable for contractor selection due to its ability to handle conflicting criteria and provide compromise solutions. VIKOR provides a systematic approach to identify the best compromise solution among various alternatives. It considers the maximum group utility and the minimum individual regret to determine the optimal compromise solution. In the case of contractor selection, VIKOR can help weigh different criteria, consider the trade-offs between conflicting factors (e.g., cost vs. quality), and identify contractors that offer the best overall compromise (Fig. 2).

    Fig. 2
    figure 2

    The criteria influencing contractor selection

    Full size image

The computation of these decision-making algorithms can be summarized in the following stages (Darbari et al. 2019; Di Bona et al. 2019):

  1. 1.

    Identify the contractor criteria that influence the construction project rate. In this paper seven criteria were selected which are: (a)Tender price (TP), (b) Accomplishment time (AT), (c) Safety (S) that includes the reputation of an organization,(d) Technical capability (TC),(e) Management capability (MC) as project-specific criteria evaluating the contracting company's level of technical and management skills, (f) Experience in comparable jobs (E) to evaluate the level of experience presented by the contractor and (g) Economic status (ES) that represents the contracting company's financial strength.

  2. 2.

    Using the AHP method of MCDM in the computation of the weight of each criteria after determination of the relative importance of criteria according to specialists. AHP provides more flexibility in (a) dealing with qualitative criteria to determine how well each contractor "satisfies" or "scores" for each criterion, and (b) assigning weights of relative importance to each criterion to assign these values based on the decision maker's preferences. The AHP's basic scale is used to input the judgments. A property is always allotted the value 1 when compared to itself, the primary diagonal elements of the pairwise comparison matrix are all 1. The numerals 3, 5, 7, and 9 correlate to the verbal judgments "moderate significance," "strong importance," "extremely strong importance," and "absolute importance," respectively, with 2, 4, 6, and 8 representing a compromise between the preceding values. With n features assumed, the pairwise comparison of feature I with feature j provides. a square matrix that indicates the relative significance of attribute I for j. \(a_{ij} = 1\) when i = j and \(a_{ji} = 1/a_{ij}\) The pairwise comparison matrix below shows how much each contractor performs for each qualitative criterion. There are five square matrices considering six contractors. \(A_{6*6}\) where, as an example \(a_{52}\) Contractor 5 technical capability indicates how well he performs in comparison to Contractor 2. In this instance \(a_{52}\) = 5 suggests that in terms of technical capability for contractors 5 is strong than 2.

  3. 3.

    Utilize two methods in parallel VIKOR and TOPSIS to prioritize the available contractors for a construction project. VIKOR and TOPSIS procedures will be discussed in detail in the following sections.

2.1 TOPSIS Method

These computations of the TOPSIS method can be summarized in the following steps (Vahdani et al. 2013; Bognár et al. 2022; Irfan et al. 2022):

  1. 1.

    Compute the normalized decision matrix. The normalized value (\({r}_{ij}\)) is computed as

    $$r_{ij} = \frac{{f_{ij} }}{{\sqrt {\sum\limits_{j = 1}^{j} {f_{ij}^{2} } } }}$$
    (1)

    where j = number of alternatives; i = a number of criteria; and \(f_{ij}\) = value of the j alternative for the I criteria.

  2. 2.

    Compute the weighted decision matrix. The normalized weighted value (\({v}_{ij}\)) is computed as

    $${\text{v}}_{{\text{i}}} = {\text{w}}_{{\text{i}}} r_{ij}$$
    (2)

    where \({{\text{w}}}_{{\text{i}}}\) = weight of the ith criterion or attribute \(inhich {\sum }_{i=1}^{n}{w}_{i}\)= 1.

  3. 3.

    Determine the ideal (\({A}^{*}\)) and negative ideals (\({A}^{-}\)) solutions:

    $$A^{*} = \{ v_{1}^{*} , \ldots ,v_{n}^{*} \} = \{ (\max_{j} v_{ij} i \in I^{\prime}),(minv_{ij} |i \in I{^{\prime\prime}})\} \quad {\text{Positive}}\;{\text{ideal}}\;{\text{solution}}$$
    (3)
    $$A^{ - } = \{ v_{1}^{ - } , \ldots ,v_{n}^{ - } \} = \{ (\min_{j} v_{ij} i \in I^{\prime}),(\max v_{ij} |i \in I{^{\prime\prime}})\} \quad {\text{negative}}\;{\text{ideal}}\;{\text{solution}}$$
    (4)

    where \({I}^{\mathrm{^{\prime}}}\) is associated with benefit criteria, and \({I}^{"}\) is associated with cost criteria.

  4. 4.

    Calculate the separation measures, using the n-dimensional Euclidean distance, the separation of each alternative from the ideal solution is computed as

    $$D_{j}^{*} = \sqrt {\sum\limits_{i = 1}^{n} {(v_{ij} - v_{i}^{*} )^{2} } } \quad {\text{j}} = {1}, \ldots .,{\text{ J}}$$
    (5)

    Similarly, the separation from the negative ideal solution is given as

    $$D_{j}^{ - } = \sqrt {\sum\limits_{i = 1}^{n} {(v_{ij} - v_{i}^{ - } )^{2} } } \quad {\text{j}} = {1}, \ldots .,{\text{ J}}$$
    (6)
  5. 5.

    Calculate the relative closeness to the ideal solution.

    $$P_{j}^{*} = \frac{{D_{j}^{ - } }}{{(D_{j}^{*} + D_{j}^{ - } )}}\quad 0 \le \le {1}, \;{\text{j}} = {1}, \ldots .,{\text{J}}$$
    (7)
  6. 6.

    Rank the preference order by ranking the alternative contractors based on their relative closeness values from the best contractor that has maximum relative closeness value (\({P}_{j}^{*}\)) to worst one.

2.2 VIKOR method

VIKOR Step-by-Step Procedure as follows(Mardani et al. 2016):

  1. 1.

    1. Determine the best and the worst values of all criterion functions from each alternative. If the ith function represents a benefit, then \(f_{i}^{*}\) =  \(\max_{j} f_{ij}\) and \(f_{i}^{ - }\) = \(\min_{j} f_{ij}\) whereas if the i-th function represents a cost,

\(f_{i}^{*}\) =  \(\min_{j} f_{ij}\) and \(f_{i}^{ - }\) =  \(\max_{j} f_{ij}\).

  1. 2.

    Step 2: Compute the values \(S_{j}\) and \(R_{j}\), j = 1, 2; …j by the relations

    $$S_{j} = \sum\limits_{i = 1}^{n} {w_{i} (f_{i}^{*} - f_{ij} } )/(f_{i}^{*} - f_{i}^{ - } )$$
    $$R_{j} = \max_{i} \left[ {w_{i} (f_{i}^{*} - f_{ij} )/(f_{i}^{*} - f_{i}^{ - } )} \right]$$

    where \(S_{j}\) represents the maximum group of the utility of the majority (concordance) of alternative j; \(R_{j}\) represents a minimum of individual regret of the opponent (discordance) of alternative j; and \(w_{i}\) = weights of criteria, expressing the decision maker’s preference as the relative importance of the criteria.

  2. 3.

    Compute the values \(Q_{j}\), j = 1, 2; …j by the relations.

    $$Q_{j} = v(S_{j} - S^{*} )/(S^{ - } - S^{*} ) + (1 - v)(R_{j} - R^{*} )/(R^{ - } - R^{*} )$$

    where, where \(Q_{j}\) represents the solution of alternative j; \(S^{*}\) = \(\min_{j} S_{j}\); \(R^{ - } = \max_{j} R_{j}\) and v is introduced as a weight for the strategy of maximum group utility, whereas \((1 - v)\) = weight of the individual regret. The solution obtained by \(\min_{j} S_{j}\) is with a maximum group utility (majority rule), and the solution obtained by \(\min_{j} R_{j}\) is with a minimum individual regret of the opponent. Normally, the value of v is taken as 0.5. However, v can take any value from 0 to 1.

  3. 4.

    Rank the alternatives, sorted by the values S, R, and Q, in decreasing order. The results are three ranking lists.

  4. 5.

    Propose as a compromise solution the alternative (\(A^{\prime}\))which is ranked the best by the measure Q (minimum) if the following two conditions are satisfied:

    1. a.

      condition (1); Acceptable advantage: where \(DQ = 1/(J - 1)\), and \(A^{(2)}\) = alternative with the second position on the ranking list by Q: \(J\) = the number of alternatives.

    2. b.

      condition (2); Acceptable stability in decision making: Alternative \(A^{1}\) must also be the best ranked by S or/and R. This compromise solution is stable within a decision-making process, which could be: ‘‘voting by majority rule’’(when v > 0:5 is needed), or ‘‘by consensus’’ \(v \approx 0.5\) or ‘‘with veto’’ (v < 0:5). Here, v is the weight of the decision-making strategy ‘‘the majority of criteria’’ (or ‘‘the maximum group utility). If one of the conditions is not satisfied, then a set of compromise solutions is proposed, which consists of:

    3. c.

      Alternative \(A^{1}\) and \(A^{2}\) if only condition (2) is not satisfied.

    4. d.

      Alternative,\(A^{2}\) \(A^{M}\) if condition (1) is not satisfied; and is determined by the relation:

\(Q(A^{M} ) - Q(A^{\prime}) < DQ\) for maximum \(M\) (the positions of these alternatives are ‘‘in closeness’’).

3 Case study

A real-life example of contractor selection to construct a bridge in the region of east Cairo in Egypt is analyzed to illustrate the use of the current MCDM algorithms and demonstrate its capabilities. The project of the intersection of Mustafa Bridge with Abbas Al-Akkad in Nasr City is a continuation of the bridge projects in the region to solve the problem of traffic congestion and facilitate the citizens. The bridge includes 3 lanes in each direction with a total length of 570 and 21.5 m width, as shown in Fig. 3. Only six contractors were eligible for this project.

Fig. 3
figure 3

Mostafa El Nahass bridge

Full size image

3.1 Data collection

The required data for these contractors were summarized based on the available data that were provided by the Egyptian Roads and Bridges Authority. The data for selecting the contractor was collected from different experts, levels, and sources, and consultants in construction and maintenance projects. The opinions were compiled and compared between them independently. The priority of selecting the appropriate contractor for the project was determined through several criteria arranged after matching the opinions of field experts after getting high consistency between all data that were collected.

  1. (1)

    Tender price (TP) and accomplishment time (AT) for the eligible contactors as shown in Table 1.

    Table 1 Tender price and accomplishment time for each contractor
    Full size table
  2. (2)

    Relative importance for criteria; Safety (S), Technical capability (TC), Management capability (MC), Experience in comparable jobs (E), and Economic status (ES) for six contractors as shown in matrices 1 to 5.

  1. (1)

    Technical capability (TC): \({\text{TC}}= \left[ {\begin{array}{*{20}c} 1 & 5 & 4 & 5 & 3 & 2 \\ {1/5} & 1 & {1/7} & {1/3} & {1/6} & {1/3} \\ {1/4} & 7 & 1 & 2 & 3 & 2 \\ {1/5} & 3 & {1/2} & 1 & {1/4} & {1/3} \\ {1/3} & 6 & {1/3} & 4 & 1 & 2 \\ {1/2} & 3 & {1/2} & 3 & {1/2} & 1 \\ \end{array} } \right]\)

  2. (2)

    Experience in the same works (E): \({\text{E}} = \left[ {\begin{array}{*{20}c} 1 & 3 & 4 & 5 & 6 & 3 \\ {1/3} & 1 & 2 & 3 & 5 & 4 \\ {1/4} & {1/2} & 1 & 2 & 3 & 4 \\ {1/5} & {1/3} & {1/2} & 1 & 4 & 3 \\ {1/6} & {1/5} & {1/3} & {1/4} & 1 & {1/2} \\ {1/3} & {1/4} & {1/4} & {1/3} & 2 & 1 \\ \end{array} } \right]\)

  3. (3)

    Safety(S): S = \(\left[ {\begin{array}{*{20}c} 1 & {1/2} & {1/3} & {1/5} & {1/4} & {1/2} \\ 2 & 1 & 2 & 3 & 3 & 4 \\ 3 & {1/2} & 1 & {1/3} & {1/2} & 1 \\ 5 & {1/3} & 3 & 1 & 2 & 5 \\ 4 & {1/3} & 2 & {1/2} & 1 & 2 \\ 2 & {1/4} & 1 & {1/5} & {1/2} & 1 \\ \end{array} } \right]\)

  4. (4)

    Management capability(MC): MC =  \(\left[ {\begin{array}{*{20}c} 1 & {1/2} & {1/5} & {1/4} & {1/5} & {1/3} \\ 2 & 1 & {1/2} & {1/3} & {1/4} & {1/5} \\ 5 & 2 & 1 & {1/3} & {1/4} & {1/2} \\ 4 & 3 & 3 & 1 & {1/5} & {1/3} \\ 5 & 4 & 4 & 5 & 1 & 2 \\ 3 & 5 & 2 & 3 & {1/2} & 1 \\ \end{array} } \right]\).

  5. (5)

    Economic status: ES = \(\left[ {\begin{array}{*{20}c} 1 & {1/2} & {1/7} & 1 & {1/2} & {1/3} \\ 2 & 1 & {1/5} & {1/3} & {1/4} & {1/2} \\ 7 & 5 & 1 & 5 & 2 & 3 \\ 1 & 3 & {1/5} & 1 & {1/3} & {1/4} \\ 2 & 4 & {1/2} & 3 & 1 & {1/2} \\ 3 & 2 & {1/3} & 4 & 2 & 1 \\ \end{array} } \right]\)

4 Computations and results

  1. 1.

    The vector \(W = \left[ {W_{1} ,W_{2} ,..,W_{n} } \right]\), Which provides the weight assigned to each criteria in pairwise comparison matrix A, must be known. A two-step process is described to derive the vector W from A: Divide every entry in A’s column i by the total of the entries in column i. This results in a new matrix called a normalized matrix, the total of the elements in each column is (1) \(W_{i}\) is calculated as the average of the elements in row i of the normalized matrix.

Table 2 shows the computed weights for each criteria. After obtaining the pairwise comparison matrices, it must be checked for consistency. Minor discrepancies are typical and do not pose major problems. To ensure consistency in the decision maker's comparisons, apply the four-step approach shown below. W will now represent the decision-weight maker's estimate:

Table 2 Calculated criteria weight among contractors
Full size table
  1. 2.

    Calculate \(AW^{T}\), in which A is the pairwise comparison matrix and T indicates transpose.

  2. 3.

    Determine the maximal eigenvalue \(\lambda_{\max } = \frac{1}{n}\sum\nolimits_{i = 1}^{n} {i_{th} }\) entry in \(AW^{T}\)/\(i_{th}\) in \(W^{T}\).

  3. 4.

    Calculate the consistency index (CI) as a process \(CI = \frac{{\left( {\lambda_{\max } } \right) - 1}}{n - 1}\), The lower the CI, the lower the deviation from consistency. If CI is small enough, the decision-comparison makers are likely to be consistent enough to provide reliable estimates of the weights for their target. for a completely consistent decision maker, ith entry in \(AW^{T}\) = n (ith entry of \(W^{T}\)). This indicates that a completely consistent decision-maker has CI = 0.

  4. 5.

    Contrast the consistency index with the random index. For the proper value of n in decision making \((CI/RI) < 0.10,\) Although the degree of consistency is favorable, if \((CI/RI)\) > 0:10, There may be severe inconsistencies, and the AHP may not produce useful significant outcomes.

Table 3 displays the random index for various n values and Table 4 displays the eigenvalue (max) and consistency ratio (CI/RI) for each qualitative criterion. All of the consistency ratios are smaller than the maximum of 0.1. As a result, the decisions made are quite consistent.

Table 3 Values of random index
Full size table
Table 4 Eigenvalue (λmax) and consistency ratio (CI/RI) for each qualitative criteria:
Full size table

The next step is to give relative relevance weights to each criterion. Following the same methods as before, the decision makers create the pairwise comparison matrix below based on their preferences.

The item in this pairwise comparison matrix's row I and column j reflects how much more significant criteria i is than j in terms of the project's aim.

$$\left[ {\begin{array}{*{20}c} 1 & 5 & 9 & 3 & 5 & 7 & 4 \\ {1/5} & 1 & 5 & {1/3} & {1/2} & 5 & {1/3} \\ {1/9} & {1/5} & 1 & {1/5} & {1/7} & {1/3} & {1/5} \\ {1/3} & 3 & 5 & 1 & {1/2} & 3 & {1/4} \\ {1/5} & 2 & 7 & 2 & 1 & 5 & {1/3} \\ {1/7} & {1/5} & 3 & {1/3} & {1/5} & 1 & {1/5} \\ {1/4} & 3 & 5 & 4 & 3 & 5 & 1 \\ \end{array} } \right]$$

The weight of each criteria was computed as follows: \(W_{TP}\) = 0.39, \(W_{AT}\) = 0.11,\(W_{S}\) = 0.21,\(W_{ES}\) = 0.14, \(W_{E}\) = 0.09,\(W_{TC}\) = 0.04, and \(W_{MC}\) = 0.02 as shown in Fig. 4. Eigenvalue (λmax) computed equal 7.7685 and the consistency ratio (CI/RI) is 0.098, which is less than the maximum allowable value of < 0.1 As a result, the decisions made are consistent.

Fig. 4
figure 4

Classification and weight of criteria

Full size image

4.1 The TOPSIS and VIKOR algorithms

Table 5 displays the statistics for the six contractors and seven selection criteria. The tender price and accomplishment time parameters are based on the data supplied by the contractors when submitting the bids for the bridge. Technical capability, experience, economic status, managerial capability, and safety are all good traits, hence higher values are preferred. Tender price and accomplishment time are unfavorable characteristics, lower values are preferred.

Table 5 Statistics for the six contractors and seven selection criteria
Full size table

4.2 The normalized decision matrix and the weight normalized matrix corresponding to steps 1 and 2 are produced using The TOPSIS technique

  • Matrix normalization

    $$\left[ {\begin{array}{*{20}c} {0.408} & {0.293} & {0.756} & {0.799} & {0.122} & {0.133} & {0.097} \\ {0.412} & {0.335} & {0.079} & {0.443} & {0.143} & {0.692} & {0.134} \\ {0.405} & {0.418} & {0.451} & {0.298} & {0.799} & {0.234} & {0.246} \\ {0.407} & {0.377} & {0.144} & {0.226} & {0.169} & {0.554} & {0.317} \\ {0.415} & {0.460} & {0.354} & {0084} & {0.353} & {0.334} & {0.766} \\ {0.402} & {0.523} & {0.272} & {0.137} & {0.415} & {0.174} & {0.474} \\ \end{array} } \right]$$

  • Weighted normalized matrix

    $$\left[ {\begin{array}{*{20}c} {0.158} & {0.033} & {0.031} & {0.071} & {0.017} & {0.028} & {0.002} \\ {0.159} & {0.038} & {0.003} & {0.039} & {0.019} & {0.145} & {0.003} \\ {0.157} & {0.047} & {0.018} & {0.027} & {0.108} & {0.049} & {0.006} \\ {0.158} & {0.043} & {0.006} & {0.020} & {0.023} & {0.116} & {0.008} \\ {0.161} & {0.052} & {0.014} & {0.007} & {0.048} & {0.070} & {0.018} \\ {0.155} & {0.059} & {0.011} & {0.012} & {0.056} & {0.036} & {0.011} \\ \end{array} } \right]$$

Table 6 shows the ideal (A) and negative-ideal (A) solutions using Eqs. (3) and (4) for the regarded aspects. Table 7 shows the values of the separation measures (\(D_{j}^{*}\) and \(D_{j}^{ - }\)) and the relative closeness to the ideal solution (C) belonging to the six contractors obtained using Eqs. (5–7), respectively. Table 8 displays the best and worst (\(f_{ij}\)).

Table 6 Ideal (\(A^{*}\)) and Negative-Ideal (\(A^{ - }\)) Solution
Full size table
Table 7 Separation Measures (, \(D_{j}^{ - }\)) and performance score (\(P_{j}^{*}\))
Full size table
Table 8 Best (\(f_{i}^{*}\)) and worst (\(f_{i}^{ - }\)) values of criteria functions
Full size table

values of all criteria functions for the VIKOR approach.

Table 9 shows the values of \(S_{j}\), and \(Q_{j}\).

Table 9 Values of \(S_{j}\), and \(Q_{j}\)
Full size table

Table 10 displays the findings acquired by the TOPSIS and VIKOR techniques. Figures 5 and 6 show the similarity of the solution between the two methods and the ranking of the contractors.

Table 10 Results obtained by Topsis and Vikor method
Full size table
Fig. 5
figure 5

The similarity between Topsis and Vikor method

Full size image
Fig. 6
figure 6

Ranking of contractor

Full size image

4.3 According to the TOPSIS and VIKOR algorithm

Contractor 2 is the best aspect of the ranking index. Additionally, being the top-ranked alternative by the VIKOR algorithm shows that it is the closest to the optimal answer. The elevated levels that Contractor 2 offers in expertise and safety, combined with the higher weights that decision-makers have allotted to these criteria, make Contractor 2 the highest-ranked contractor by both methods, even though Contractor 2 offers the highest prices and low values in technical capability, economic status, and management capability.

4.4 Applicability and limitation of model

The integration of TOPSIS, VIKOR with AHP into the model can provide a more comprehensive and robust approach to multi-criteria decision-making. This integrated model combines the strengths of each method to enhance the decision-making process. However, it is important to consider both the applicability and limitations of this integrated model:

4.4.1 Applicability

  1. 1.

    By taking into account several criteria and their weights within the AHP framework, the integrated model enables a more complete examination. It helps people make decisions by providing a methodical way to weigh options and record values.

  2. 2.

    The addition of VIKOR to the integrated model aids in finding a happy medium between benefit and cost considerations. This is especially helpful when decision-makers are trying to find a happy medium that minimizes undesirable consequences.

  3. 3.

    Handling It is possible to use both quantitative and qualitative criteria in the integrated model. Subjective opinions and linguistic evaluations may be included in AHP, while quantitative criteria can be given numerical weight in TOPSIS and VIKOR.

  4. 4.

    The integration enables decision-making flexibility by capitalizing on the benefits of both approaches. It enables decision-makers to modify the model to better fit the nature and parameters of the choice issue at hand.

4.4.2 Limitations

  1. 1.

    Increased complexity in decision-making may result from combining several approaches into a single model. It might need more time and skill to apply and understand the findings.

  2. 2.

    AHP depends significantly on the judgments and preferences of decision-makers, hence there is room for subjectivity and inconsistency in the integrated model. It's important to pay close attention so that the results are consistent and trustworthy.

  3. 3.

    The criteria weights, scores, and rankings used in the integrated model can only be as accurate as the data used to create them. In the context of making decisions in the real world, it may be difficult to collect data that is both complete and of good quality.

  4. 4.

    The computational cost may grow due to the integration of various approaches, particularly when a significant number of criteria and alternatives must be considered. Complexity may be managed with sufficient computing power and well-designed algorithms.

5 Conclusion and future scope

Recently, there has been a shift away from the lowest-tender price-wins concept in the selection of contractors for construction projects not only at the regional level but also at the worldwide level. The execution of a project may suffer if a suitable and precise approach for picking the best-suited contractor is not used. Using a multi-criteria selection strategy to aid owners in the selection of contractors for building projects. Increased project complexity, greater performance, and financial and safety constraints have necessitated the employment of multi-criteria decision-making methodologies in construction projects in Egypt. Sometimes contradictory aims and alternatives such as tender price, completion date, and expertise must be examined in these multi-criteria settings. The Topsis and Vikor algorithms were utilized in the selection of a contractor for a road construction project. The availability of data, and the absence of doubt, hence the possibility to give precise numbers to the criterion or qualities that have played a vital part in determining a technique to select a contractor. Both strategies, which have not previously been employed in contractor selection, can be generalized and applied elsewhere, increasing the number of methods accessible to decision-makers to satisfy greater performance standards. According to the results, one of the contractors is the top-ranked by both approaches. The TOPSIS method's highest-rated alternative means that this contractor is the best in terms of the ranking index. Furthermore, having the highest rated option by the VIKOR technique shows that it is the closest to the perfect solution, and is as near to the ideal answer as possible The justification for human choice is to be as close to the ideal as feasible. The TOPSIS and the VIKOR methodologies are examples of multi-criteria decision-making (MCDM) approaches that may be used to rank potential options according to many different criteria. Both approaches rank solutions by how far they are from the optimal one. The primary distinction between TOPSIS and VIKOR is that TOPSIS uses a weighted sum of the distances from the ideal answer, whereas VIKOR employs a compromise ranking approach. Furthermore, in TOPSIS, all criteria must be measured using the same units, but in VIKOR, this is not the requirement. some of the limitations of the integrated model may not take into account the inherent uncertainty or fluctuation in the criterion weights or scores. This restriction may need the use of uncertainty analysis methods or sensitivity analysis. In the future challenges and more criteria which can be tested using different MCDM techniques and considered uncertainty in the model.