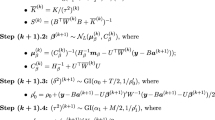Dependence Properties of B-Spline Copulas

Abstract

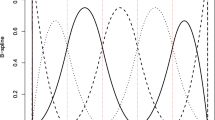
We construct by using B-spline functions a class of copulas that includes the Bernstein copulas arising in Baker’s distributions. The range of correlation of the B-spline copulas is examined, and the Fréchet–Hoeffding upper bound is proved to be attained when the number of B-spline functions goes to infinity. As the B-spline functions are well-known to be an order-complete weak Tchebycheff system from which the property of total positivity of any order follows for the maximum correlation case, the results given here extend classical results for the Bernstein copulas. In addition, we derive in terms of the Stirling numbers of the second kind an explicit formula for the moments of the related B-spline functions on the right half-line.

Appendix

Proof of Theorem 8.

We prove the statement by mathematical induction on d. Note first that (5.7) with d = 0 coincides with the boundary conditions (5.4) for all i and h.

Suppose that (5.7) is true for the case d − 1 and for all i and h, then we wish to prove that it also holds true for the case d and for all i and h.

• (i) For i ≥ 0, by the assumption of induction,

  $$ \gamma^{d-1}_{i}(h) = \sum\limits_{\ell=0}^{h} i^{\ell} \binom{h}{\ell} \frac{S(h+d-\ell,d)}{\displaystyle\binom{h+d-\ell}{d}}. $$

  Then, we have

  $$ \gamma^{d-1}_{i+1}(h) = \sum\limits_{k=0}^{h} (i+1)^{k} \binom{h}{k} \frac{S(h+d-k,d)}{\displaystyle\binom{h+d-k}{d}}, $$

  and by expanding (i + 1)^k using the binomial theorem, we obtain

  $$ \gamma^{d-1}_{i+1}(h) = \sum\limits_{k=0}^{h} \sum\limits_{\ell=0}^{k} i^{\ell} \binom{k}{\ell} \binom{h}{k} \frac{S(h+d-k,d)}{\displaystyle\binom{h+d-k}{d}}. $$

  Interchanging the order of summation and using the identity,

  $$ \binom{k}{\ell} \binom{h}{k} = \binom{h}{\ell} \binom{h-\ell}{k-\ell}, $$

  we find that

  $$ \gamma^{d-1}_{i+1}(h) = \sum\limits_{\ell=0}^{h} i^{\ell} \binom{h}{\ell} \sum\limits_{k=\ell}^{h} \binom{h-\ell}{k-\ell} \frac{S(h+d-k,d)}{\displaystyle\binom{h+d-k}{d}}. $$

  Replacing k by k − ℓ, we have

  $$ \gamma^{d-1}_{i+1}(h) = \sum\limits_{\ell=0}^{h} i^{\ell} \binom{h}{\ell} \sum\limits_{k=0}^{h-\ell} \binom{h-\ell}{k} \frac{S(h+d-\ell-k,d)}{\displaystyle\binom{h+d-\ell-k}{d}}, $$

  and using the identity,

  $$ \frac{\displaystyle\binom{h-\ell}{k}}{\displaystyle\binom{h+d-\ell-k}{d}} = \frac{\displaystyle\binom{h+d-\ell}{h+d-\ell-k}}{\displaystyle\binom{h+d-\ell}{d}}, $$

  we deduce that

  $$ \begin{array}{@{}rcl@{}} \gamma^{d-1}_{i+1}(h) &=& \sum\limits_{\ell=0}^{h} i^{\ell} \binom{h}{\ell} \frac{1}{\displaystyle\binom{h+d-\ell}{d}} \sum\limits_{k=0}^{h-\ell} \binom{h+d-\ell}{h+d-\ell-k}\\ &&\times S(h+d-\ell-k,d) \\ &= &\sum\limits_{\ell=0}^{h} i^{\ell} \binom{h}{\ell} \frac{S(h+d-\ell+1,d+1)}{\displaystyle\binom{h+d-\ell}{d}}, \end{array} $$

  (6.1)

  where the last equality follows from the identity (5.6). Moreover, using the identity,

  $$ \binom{h+1}{\ell} = \binom{h}{\ell-1} + \binom{h}{\ell}, $$

  we obtain

  $$ \begin{array}{@{}rcl@{}} &&\gamma^{d-1}_{i}(h + 1) - i \gamma^{d-1}_{i}(h) \\ &&\qquad= i^{h+1} + \sum\limits_{\ell=0}^{h} \left[ i^{\ell} \binom{h+1}{\ell} \frac{S(h+d-\ell+1,d)}{\displaystyle\binom{h+d-\ell+1}{d}} \right.\\ && \qquad\qquad\qquad\qquad \left.- i^{\ell+1} \binom{h}{\ell} \frac{S(h+d-\ell,d)}{\displaystyle\binom{h+d-\ell}{d}} \right] \\ &&\qquad= i^{h+1} + \sum\limits_{\ell=0}^{h} \left[ i^{\ell} \left\{ \binom{h}{\ell-1} + \binom{h}{\ell} \right\} \frac{S(h+d-\ell+1,d)}{\displaystyle\binom{h+d-\ell+1}{d}} \right.\\ && \qquad\qquad\qquad\qquad \left.- i^{\ell+1} \binom{h}{\ell} \frac{S(h+d-\ell,d)}{\displaystyle\binom{h+d-\ell}{d}} \right]. \end{array} $$

  (6.2)

  Since S(d, d) = 1 then

  $$ \begin{array}{@{}rcl@{}} i^{h+1} + \sum\limits_{\ell=0}^{h} i^{\ell} \binom{h}{\ell-1}\frac{S(h+d-\ell+1,d)} {\displaystyle\binom{h+d-\ell+1}{d}} &= &\sum\limits_{\ell=1}^{h+1} i^{\ell} \binom{h}{\ell-1}\frac{S(h+d-\ell+1,d)} {\displaystyle\binom{h+d-\ell+1}{d}} \\ &=& \sum\limits_{\ell=0}^{h} i^{\ell} \binom{h}{\ell}\frac{S(h+d-\ell,d)} {\displaystyle\binom{h+d-\ell}{d}}, \end{array} $$

  and substituting this result into (6.2), we obtain

  $$ \gamma^{d-1}_{i}(h+1)-i \gamma^{d-1}_{i}(h) = \sum\limits_{\ell=0}^{h} i^{\ell} \binom{h}{\ell} \frac{S(h+d-\ell+1,d)}{\displaystyle\binom{h+d-\ell+1}{d}}. $$

  (6.3)

  Similarly, it follows from Eq. (6.1) that

  $$ \begin{array}{@{}rcl@{}} &&\gamma^{d-1}_{i+1}(h+1)-i\gamma^{d-1}_{i+1}(h) {\kern12pc}\\ &&\qquad= i^{h+1} + \sum\limits_{\ell=0}^{h} \left[ i^{\ell} \binom{h+1}{\ell} \frac{S(h+d-\ell+2,d+1)}{\displaystyle\binom{h+d-\ell+1}{d}} \right. \\ && \qquad\qquad\qquad\qquad \left.- i^{\ell+1} \binom{h}{\ell} \frac{S(h+d-\ell+1,d+1)}{\displaystyle\binom{h+d-\ell}{d}} \right]{\kern4pc}\\ &&\qquad= \sum\limits_{\ell=0}^{h} i^{\ell} \binom{h}{\ell} \frac{S(h+d-\ell+2,d+1)}{\displaystyle\binom{h+d-\ell+1}{d}}. \end{array} $$

  (6.4)

  Hence, by substituting (6.3) and (6.4) into (5.3), we find that

  $$ \begin{array}{@{}rcl@{}} {\gamma^{d}_{i}}(h) &=& \frac{\gamma^{d-1}_{i}(h+1)-i \gamma^{d-1}_{i}(h)}{d} -\frac{\gamma^{d-1}_{i+1}(h+1)-i\gamma^{d-1}_{i+1}(h)}{d} +\frac{d+1}{d}\gamma^{d-1}_{i+1}(h) \\ &=& \sum\limits_{\ell=0}^{h} i^{\ell} \binom{h}{\ell} \left[ \frac{S(h+d-\ell+1,d)}{d \displaystyle\binom{h+d-\ell+1}{d}} - \frac{S(h+d-\ell+2,d+1)}{d \displaystyle\binom{h+d-\ell+1}{d}} \right.\\ && \qquad\qquad\qquad\qquad\qquad\qquad \left.+ \frac{(d+1)S(h+d-\ell+1,d+1)}{d \displaystyle\binom{h+d-\ell}{d}} \right] \\ &=& \sum\limits_{\ell=0}^{h} i^{\ell} \binom{h}{\ell} \frac{S(h+d-\ell+1,d+1)}{\displaystyle\binom{h+d-\ell+1}{d+1}}, \end{array} $$

  where the last equality follows from the recurrence formula (5.5).

• (ii) When − d < i < 0, by the assumption of induction,

  $$ \gamma^{d-1}_{i}(h) = \frac{i+d}{d} \cdot \frac{S(h+i+d,i+d)}{\displaystyle\binom{h+d}{d}}. $$

  It then follows from Eq. (5.3) that

  $$ \begin{array}{@{}rcl@{}} {\gamma^{d}_{i}}(h) &=& \frac{\gamma^{d-1}_{i}(h+1)}{i+d} + \frac{(i+d+1)\gamma^{d-1}_{i+1}(h) -\gamma^{d-1}_{i+1}(h+1)}{i+d+1} \\ &=& \frac{1}{i+d} \frac{i+d}{d} \frac{S(h+i+d+1,i+d)}{\displaystyle\binom{h+d+1}{d}} \\ &&\qquad + \frac{i+d+1}{d} \frac{S(h+i+d+1,i+d+1)}{\displaystyle\binom{h+d}{d}} \\ &&\qquad -\frac{1}{i+d+1} \frac{i+d+1}{d} \frac{S(h+i+d+2,i+d+1)}{\displaystyle\binom{h+d+1}{d}} \\ &=& \frac{i+d+1}{d+1} \frac{S(h+i+d+1,i+d+1)}{\displaystyle\binom{h+d+1}{d+1}}. \end{array} $$

  Here we used the recurrence formula (5.5) with n = h + i + d + 1 and k = i + d + 1, viz.,

  $$ \begin{array}{@{}rcl@{}} S(h+i+d+2,i+d+1) &=& (i+d+1)S(h+i+d+1,i+d+1)\\ &&+ S(h+i+d+1,i+d). \end{array} $$

• (iii) When i = −d, by the inductive hypothesis,

  $$ \gamma^{d-1}_{-d+1}(h) = \frac{h! (d-1)!}{(h+d)!}. $$

  Then, by Eq. (5.3), we have

  $$ \begin{array}{@{}rcl@{}} \gamma^{d}_{-d}(h) &=& \gamma^{d-1}_{-d+1}(h) -\gamma^{d-1}_{-d+1}(h+1) = \frac{h! d!}{(h+d+1)!}, \end{array} $$

  (6.5)

  which coincides with Eq. (5.7) with i = −d.

The proof is completed by induction on d. □