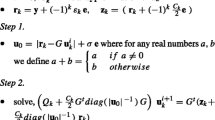Skip to main content
SpringerLink
Log in

An \(l_1\)-norm loss based twin support vector regression and its geometric extension

  • Original Article
  • Published:
International Journal of Machine Learning and Cybernetics Aims and scope Submit manuscript

Abstract

This paper proposes a novel \(l_1\)-norm loss based twin support vector regression (\(l_1\)-TSVR) model. The bound functions in this \(l_1\)-TSVR are optimized by simultaneously minimizing the \(l_1\)-norm based fitting and one-side \(\epsilon\)-insensitive losses, which results in different dual problems compared with twin support vector regression (TSVR) and \(\epsilon\)-TSVR. The main advantages of this \(l_1\)-TSVR are: First, it does not need to inverse any kernel matrix in dual problems, indicating that it not only can be optimized efficiently, but also has partly sparse bound functions. Second, it has a perfect and practical geometric interpretation. In the spirit of its geometric interpretation, this paper further presents a nearest-points based \(l_1\)-TSVR (NP-\(l_1\)-TSVR), in which bound functions are constructed by finding the nearest points between the reduced convex/affine hulls of training data and its shifted sets, respectively. Computational results obtained on a number of synthetic and real-world benchmark datasets clearly illustrate the superiority of the proposed \(l_1\)-TSVR and NP-\(l_1\)-TSVR as comparable generalization performance is achieved in accordance with the other SVR-type algorithms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Notes

  1. Available at http://archive.ics.uci.edu/ml/.

References

  1. Balasundaram S, Gupta D (2014) Training Lagrangian twin support vector regression via unconstrained convex minimization. Knowl Based Syst 59:85–96

    Article  MATH  Google Scholar 

  2. Bates DM, Watts DG (1988) Nonlinear regression analysis and its applications. Wiley, New York

    Book  MATH  Google Scholar 

  3. Bi J, Bennett KP (2003) A geometric approachto support vector regression. Neurocomputing 55:79–108

    Article  Google Scholar 

  4. Cevikalp H, Triggs B, Yavuz HS, Küçük Y, Küçük M, Barkana A (2010) Large margin classifiers based on affine hulls. Neurocomputing 73(16–18):3160–3168

    Article  Google Scholar 

  5. Chen J, Hu Q, Xue X, Ha M, Ma L (2017) Support function machine for set-based classification with application to water quality evaluation. Inf Sci 388–389:48–61

    Article  MathSciNet  Google Scholar 

  6. Crisp DJ, Burges CJC (2000) A geometric interpretation of \(\nu\)-SVM classifiers. In: Solla S, Leen T, Muller K-R (eds), Advances in neural information processing systems, pp. 244–250

  7. Eubank RL (1999) Nonparametric regression and spline smoothing, statistics: textbooks and monographs, vol 157, 2nd edn. Marcel Dekker, New York

  8. Gao S, Ye Q, Ye N (2011) 1-Norm least squares twin support vector machines. Neurocomputing 74:3590–3597

    Article  Google Scholar 

  9. Ghorai S, Mukherjee A, Dutta PK (2009) Nonparallel plane proximal classifier. Signal Process 89(4):510–522

    Article  MATH  Google Scholar 

  10. Hao P-Y (2009) Interval regression analysis using support vector networks. Fuzzy Sets Syst 160(17):2466–2485

    Article  MathSciNet  MATH  Google Scholar 

  11. Hao P-Y (2010) New support vector algorithms with parameteric insensitive /margin model. Neural Netw 23(1):60–73

    Article  MATH  Google Scholar 

  12. Hsu CW, Lin CJ (2002) A comparison of methods for multiclass support vector machines. IEEE Trans Neural Netw 13:415–425

    Article  Google Scholar 

  13. Jayadeva R, Khemchandani R, Chandra S (2007) Twin support vector machines for pattern classification. IEEE Trans Pattern Anal Mach Intell 29(5):905–910

    Article  MATH  Google Scholar 

  14. Khemchandani R, Goyal K, Chandra S (2016) TWSVR: regression via twin support vector machine. Neural Netw 74:14–21

    Article  MATH  Google Scholar 

  15. Khemchandani R, Saigal P, Chandra S (2016) Improvements on \(\nu\)-twin support vector machine. Neural Netw 79:97–107

    Article  Google Scholar 

  16. Kohavi R (1995) A study of cross-validation and bootstrap for accuracy estimation and model selection. In: Proceedings of the 14th international joint conference on A.I., no. 2, Canada

  17. Lee W, Jun CH, Lee JS (2017) Instance categorization by support vector machines to adjust weights in AdaBoost for imbalanced data classification. Inf Sci 381:92–103

    Article  Google Scholar 

  18. López J, Barbero Á, Dorronsoro JR (2011) Clipping algorithms for solving the nearest point problem over reduced convex hulls. Pattern Recognit 44(3):607–614

    Article  MATH  Google Scholar 

  19. Mangasarian OL (1994) Nonlinear programming. SIAM, Philadelphia

    Book  MATH  Google Scholar 

  20. Mavroforakis ME, Theodoridis S (2006) A geometric approach to support vector machine (SVM) classification. IEEE Trans Neural Netw 17(3):671–682

    Article  Google Scholar 

  21. Mercer J (1909) Functions of positive and negative type and the connection with the theory of integal equations. Philos Trans R Soc Lond Ser A 209:415–446

    Article  MATH  Google Scholar 

  22. Parastalooi N, Amiri A, Aliheidari P (2016) Modified twin support vector regression. Neurocomputing 211(26):84–97

    Article  Google Scholar 

  23. Peng X (2010) A \(\nu\)-twin support vector machine (\(\nu\)-TSVM) classifier and its geometric approaches. Inf Sci 180:3863–3875

    Article  MATH  Google Scholar 

  24. Peng X (2010) TSVR: an efficient twin support vector machine for regression. Neural Netw 23(3):365–372

    Article  MATH  Google Scholar 

  25. Peng X (2010) Primal twin support vector regression and its sparse approximation. Neurocomputing 73(16–18):2846–2858

    Article  Google Scholar 

  26. Peng X (2011) TPMSVM: a novel twin parametric-margin support vector machine for pattern recognition. Pattern Recognit 44(10–11):2678–2692

    Article  MATH  Google Scholar 

  27. Peng X (2012) Efficient twin parametric insensitive support vector regression model. Neurocomputing 79:26–38

    Article  Google Scholar 

  28. Peng X, Wang Y (2012) Geometric algorithms to large margin classifier based on affine hulls. IEEE Trans Neural Netw 23(2):236–246

    Article  Google Scholar 

  29. Peng X, Xu D, Kong L, Chen D (2016) \(L_1\)-norm loss based twin support vector machine for data recognition. Inf Sci 340C341:86–103

    Article  MATH  Google Scholar 

  30. Peng X, Xu D, Shen J (2014) A twin projection support vector machine for data regression. Neurocomputing 138:131–141

    Article  Google Scholar 

  31. Shao Y, Zhang C, Wang X, Deng N (2011) Improvements on twin support vector machines. IEEE Trans Neural Netw 22(6):962–968

    Article  Google Scholar 

  32. Singh M, Chadha J, Ahuja P, Jayadeva R, Chandra S (2011) Reduced twin support vector regression. Neurocomputing 74:1474–1477

    Article  Google Scholar 

  33. Shao Y, Zhang C, Yang Z, Jing L, Deng N (2013) An \(\epsilon\)-twin support vector machine for regression. Neural Comput Appl 23(1):175–185

    Article  Google Scholar 

  34. Shevade SK, Keerthi SS, Bhattacharyya C, Murthy KRK (2000) Improvements to the SMO algorithm for SVM regression. IEEE Trans Neural Netw 11(5):1188–1193

    Article  Google Scholar 

  35. Staudte RG, Sheather SJ (1990) Robust estimation and testing: Wiley series in probability and mathematical statistics. Wiley, New York

    Book  MATH  Google Scholar 

  36. Tanveer M, Shubham K, Aldhaifallah M, Ho SS (2016) An efficient regularized K-nearest neighbor based weighted twin support vector regression. Knowl Based Syst 94:70–87

    Article  Google Scholar 

  37. Tao Q, Wu G, Wang J (2008) A general soft method for learning SVM classifiers with \(L_1\)-norm penalty. Pattern Recognit 41(3):939–948

    Article  MATH  Google Scholar 

  38. Vapnik VN (1995) The natural of statistical learning theory. Springer, New York

    Book  MATH  Google Scholar 

  39. Vapnik VN (1998) Statistical learning theory. Wiley, New York

    MATH  Google Scholar 

  40. Weisberg S (1985) Applied linear regression, 2nd edn. Wiley, New York

    MATH  Google Scholar 

  41. Xu Y, Yang Z, Pan X (2017) A novel twin support-vector machine with pinball loss. IEEE Trans Neural Netw Learn Syst 28(2):359–370

    Article  MathSciNet  Google Scholar 

  42. Yang Z, Hua X, Shao Y, Ye Y (2016) A novel parametric-insensitive nonparallel support vector machine for regression. Neurocomputing 171:649–663

    Article  Google Scholar 

  43. Ye Y, Bai L, Hua X, Shao Y, Wang Z, Deng N (2016) Weighted Lagrange \(\varepsilon\)-twin support vector regression. Neurocomputing 197:53–68

    Article  Google Scholar 

  44. Zhao Y, Zhao J, Zhao M (2013) Twin least squares support vector regression. Neurocomputing 118:225–236

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Shanghai Normal University, Shanghai, 200234, China

    Xinjun Peng & De Chen

Authors
  1. Xinjun Peng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. De Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xinjun Peng.

Ethics declarations

Conflict of interest

We declare that we have not any conflict with other people or organizations that can inappropriately influence our work.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Peng, X., Chen, D. An \(l_1\)-norm loss based twin support vector regression and its geometric extension. Int. J. Mach. Learn. & Cyber. 10, 2573–2588 (2019). https://doi.org/10.1007/s13042-018-0892-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13042-018-0892-8

Keywords

Search

Navigation