Introduction

Hydrological models and early warning systems related to the forecasting of extreme hydrological phenomena rely on accurate and readily available information for input variables, such as precipitation. Ground measurements form an essential source of information; nevertheless, the operation of such networks still does not provide adequate coverage, resulting in poor gauged or even ungauged basins (Lakshmi 2004). Accurate precipitation estimates are of paramount importance for any hydrological model to operate reliably, as they represent the input of water to the hydrological system. Precipitation is also an important parameter for weather prediction and climate change research (Lu and Yong 2018; Ricciardelli et al. 2018). Therefore, grid-based precipitation with high accuracy and high-quality spatiotemporal resolution is vital for climatology and hydrological researches at various scales (Duan and Bastiaanssen 2013; Ma et al. 2020). The scarcity of ground-based precipitation observations constitutes remotely sensed precipitation a precious tool for hydrological assessment, as long as remotely sensed information captures the spatial and temporal variability of precipitation. Satellite-based precipitation estimates (SPEs) have the advantage of high coverage and easy access to the data, which is an effective tool to acquire precipitation at local, regional or global scale (Kidd and Levizzani 2011). Previous research has shown that SPEs can offer precious input to hydrological models to enhance their performance in basins, where rain gauges are sparse (Le et al. 2020). However, low spatial resolution of the existing SPEs products is sometimes restrictive and their downscaling is necessary, because their spatial resolution is too coarse for use at the regional and basin scales or for parameterizing either hydrological or meteorological models at a local scale. Meanwhile, satellite precipitation is found useful for the improvement of spatial and temporal resolution not only for other remotely sensed products, such as Total Water Storage Anomalies from the Gravity Recovery and Climate Experiment (GRACE) (Gemitzi et al. 2021), but also for reanalysis and observation-based data (Sheffield et al. 2006).

Nowadays, precipitation is considered an important variable in climatological, ecological and hydrological studies, because it constitutes part not only of the energy balance but also of the water cycle too (Ghajarnia et al. 2015). Obtaining high temporal and high spatial resolution precipitation is crucial, mainly for the understanding of global climate change, since global warming has a detrimental effect on the hydrological cycle, altering the atmosphere’s water vapor capacity and the evaporation rate, resulting in changes in precipitation intensity and occurrences. This can lead to increasing and more frequent wet or dry extremes (Held and Soden 2006; Giorgi et al. 2011). Remote sensing is offering a solution in detecting these changes with reliable estimates of precipitation over large areas; however, the size of the pixel of the satellite precipitation data sets is too coarse to be applied either in hydrological and/or in meteorological studies, especially at the local or regional scales (Michaelides et al. 2009; Duan and Bastiaanssen 2013). Therefore, before using satellite precipitation products in several studies, downscaling is required not only to improve the accuracy of satellite-based data sets and to make their contribution meaningful even at local scales but also to improve hydrological forecasts. In recent years, several studies aiming to ameliorate the spatial resolution of satellite-based precipitation estimates are presented and many algorithms have been suggested for that purpose.

Research on satellite-derived precipitation has received increasing interest, and various SPEs have been produced, mainly relying on the satellite observations provided by the synergistic operation of both passive and active sensors that detect radiation of clouds in the atmosphere. The first mission dedicated to the study of tropical and subtropical precipitation was TRMM, launched in 1997, introducing for the first time the Precipitation Radar to acquire information on processes within clouds that lead to precipitation. TRMM operated until 2015 and was followed by the GPM mission, with the new Dual-frequency Precipitation Radar (DPR) (Levizzani and Cattani 2019).

Besides the remotely sensed precipitation data sets originating from TRMM or GPM retrievals, there are climatology products that combine remotely sensed observations with ground information to acquire consistent climatology data sets, useful in hydrological forecasts, drought and flood monitoring. Thus, several products relying on the satellite retrievals combined with ground gauge stations were introduced to the scientific community, such as the Global Satellite Mapping Precipitation (GSMaP) product (Kubota et al. 2006), the Precipitation Estimation from Remote Sensing Information using Artificial Neural Network–Climate Data Record (PERSIANN–CDR) data set (Ashouri et al. 2015), the Multi-Source Weighted-Ensemble Precipitation (MSWEP) data set (Beck et al. 2017), the Climate Hazards Group Infrared Precipitation with Stations (CHIRPS) data set (Funk et al. 2015), the Global Land Data Assimilation System (GLDAS) product (Rodell et al. 2004), the SM2RAIN product (Massari et al. 2020; Filippucci et al. 2022).

Although all the above-mentioned precipitation data sets are useful in many different applications, satellite derived precipitation and especially the GPM IMERG product, is of particular importance for near real time applications as its latency (with a minimum latency of ~ 4 h for GMP Early Run) can support the requirements of an early warning system. Nevertheless, its spatial resolution (~ 10 km for GPM IMERG) constraints its wide applicability and that is why downscaling is often required. Downscaling, however, can improve considerably and enhance both the spatial and temporal dimension of precipitation data sets. Most downscaling efforts have focused on either TRMM or GPM missions, although the same approaches can be applied to the rest of precipitation data sets.

Different precipitation downscaling methods exist. However, for practical reasons, the end user in a specific region can apply only few of the available methods. For this reason, review studies are helpful to point out the uncertainty associated with the researcher’s final choice of the precipitation downscaling method. Sarr et al. (2015) mentioned that the final choice of the downscaling method is very important, mainly in the fields of decision-making and regional planning.

There are two main approaches for downscaling satellite derived precipitation: statistical downscaling and dynamical downscaling (Sachindra and Perera 2016). The statistical downscaling depends on the empirical statistical relationships between subject variable and auxiliary variables. It is a highly efficient method which has been widely used for satellite-based precipitation downscaling in recent studies (Jia et al. 2011; Duan and Bastiaanssen 2013; Chen et al. 2015; Shi et al. 2015; Sharifi et al. 2019). The results of the statistical downscaling, could be strongly influenced by data errors if the predictor does not consider dominant climatic features (Di Vittorio and Miller 2013). Moreover, according to Fowler et al. (2007), statistical methods consist of a variety of approaches, which use experimental multiscale statistical relationships, parameterized by environmental predictors and other observations. Precipitation over a region is better represented as an ensemble of multiscales (multifractal), where each scale has a certain spectrum of rainfall (Deidda et al. 1999; Lovejoy and Schertzer 2006; Lovejoy et al. 2008). Thus, the precipitation process is often simulated using a multiple random cascade model, which captures the multi-scaling characteristics of the rain, assuming that the scale-invariance is within the desirable spatial and temporal scale range (Over and Gupta 1994; Groppelli et al. 2011). This existence of multifractal scale invariance of rainfall in space and time has been introduced in the 1980s and has been documented from many researchers in the past (Olsson et al. 1993; Over and Gupta 1996; Harris et al. 1998; Deidda et al. 1999; de Montera et al. 2009; Gires et al. 2013). It was considered as a valuable analysing tool especially for radar data (Tessier et al. 1993). Figure 1 shows a schematic representation of the construction of a one dimensional multifractal ‘a model’ cascade, adapted from Lovejoy and Schertzer (2006).

Fig. 1
figure 1

Schematic representation of the construction of a one-dimensional multifractal ‘a model’ cascade. The vertical axis shows the boosts and decreases in energy flux density. At each step the horizontal scale is divided by two. λ = L/Ld, where L = a large external scale, and Ld = the small dissipation scale [adapted from Lovejoy and Schertzer (2006)]

Full size image

On the other hand, dynamical downscaling is based on the mathematical representations of the complex physical process of atmosphere, ocean and land surface. It relies on regional climate models and requires intensive computational cost and large data volume, which limit its applicability (Wilby and Wigley 2000; Sylla et al. 2009; Sachindra and Perera 2016). Dynamical downscaling methods do not produce significantly better results for precipitation and are often considered too computationally demanding (Hellström et al. 2001), but when compared to statistical downscaling, they are less demanding in terms of actual data ingestion. It is worth noting, though, that the newly developed Cloud-Resolving Models (CRMs), which are used for the investigation of the mesoscale dynamics of intense precipitation system at a fine scale, could offer a potential and promising approach for the dynamical downscaling of remote sensing precipitation estimates (Matsui et al. 2016; Satoh et al. 2019).

In general, according to Gutmann et al. (2012), the statistical downscaling methods are based on current estimations of the spatial distributions of several important meteorological variables, such as temperature and precipitation, assuming that the small-scale spatial distribution will not change significantly in a modified climate. On the other hand, the dynamical downscaling approaches can resolve inherent dynamics of precipitation (Schmidli et al. 2007), providing hydrometeorological variables, which are physically accordant with the downscaled precipitation and are necessary for many hydrological models. Thus, according to all above reasons, the dynamical methods of precipitation downscaling seem to have the same goal with the statistical methods, i.e., the successful downscaling of the SPEs, improving their information content and usability accordingly.

Downscaling of satellite precipitation has attracted attention of various environmental scientists, especially during the last decade. Previous downscaling efforts were merely focused on bridging the gap between Global Climate Models (GCMs) or Regional Climate Models (RCMs) and local weather/climate observations (Maraun et al. 2010). The main purpose of this review study is to offer researchers knowledge on the topic of precipitation downscaling methods, to identify gaps in research and inconsistencies in previous studies, to critically comment on the methodology and results of previously published works and finally to identify future research trends and challenges. Thus, this study can be regarded as a practical guide for any researcher who plans to apply a downscaling method, to use the most appropriate downscaling approach to achieve the desired result in terms of spatial and temporal resolution.

Precipitation data sets—products

Satellites are categorized, according to their orbit, to Low Orbiting Satellites (LOS), scanning the Earth from an altitude of 400–800 km, following a sun-synchronous orbit and to Geostationary Satellites (GS), orbiting the Earth at an altitude of approx. 36,000 km. GS appear stationary over a set position, because they are synchronized with the Earth's rotation. The LOS that are used for precipitation investigation purposes are equipped with Infrared (IR), Visible (VIS), Active Microwave (AMW) and Passive Microwave (PMW) sensors, while GS are equipped mostly with IR and VIS instrumentation. IR sensors, by measuring the cloud’s temperature and with the performance of statistical methods, have been used to establish a relation between cloud’s temperature and precipitation. However, this indirect relationship is subject to large changes over the course of rain events. On the other hand, VIS sensors can detect precipitation by measuring the clouds’ brightness, a relationship that is poor and can be used only during daytime (Kidd and Huffman 2011). The AMW sensors measure the radiation backscatter from precipitation, which is not always a robust criterion, because attenuation effects can be substantial in heavy precipitation events (Iguchi et al. 2000). Finally, the PMW sensors can detect precipitation by measuring the change of the microwaves radiation emitted from the Earth which interacts with the rain droplets in the atmosphere. Caution should be given, though, interpreting the measurements over different regions, since the precipitation detection techniques are different over land and ocean. In addition, PMW are currently installed only onboard LOS, which hinders the continuous provision of precipitation observations (Kidd and Huffman 2011). Despite the various difficulties encountered in acquiring accurate satellite precipitation data sets, constant validation efforts using ground observations provide improved SPEs at near-real time, while the combination of satellite precipitation with ground observations, cloud resolving models and land data assimilation system present a huge potential for improved precipitation products, contributing thus to better representation of the hydro-meteorological conditions (Belay et al. 2022).

There are several precipitation products and data sets that have been used in downscaling applications. Even though our review is based on previous works using TRMM and GPM–IMERG precipitation data sets, mainly because they are the state-of-the-art SPEs used for the production of all other climatology data sets, a short description of the other precipitation data sets is also presented.

TRMM products

GPM and TRMM observations are processed to acquire precipitation estimates. TRMM precipitation is based on the TRMM Multisatellite Precipitation Analysis (TMPA) algorithm (Huffman et al. 2007) and is released with the TRMM 3B42 3-h temporal resolution and a 0.25 degree spatial resolution. GPM measurements are processed with the Integrated Multi-satellite Retrievals for Global Precipitation Measurement (IMERG) algorithm to extract precipitation estimates at the half-hour time step with a 0.1° spatial resolution (Hou et al. 2014).

The TRMM 3B42 3-hourly product with coverage 50°N–50°S is derived from different microwave imagers and IR sensors (Huffman et al. 2007). The precipitation data from microwave imagers are collected by a large number of satellites, namely, TRMM (TRMM Microwave Imager), Aqua (Advanced Microwave Scanning Radiometer-Earth Observing System, AMSR-E), United States Air Force Defense Meteorological Satellite Program (DMSP) Block 5D-2 satellites (Special Sensor Microwave Imager, SSMI, and Special Sensor Microwave Imager/Sounder, SSMIS), National Oceanic and Atmospheric Administration (NOAA) satellites NOAA-15, NOAA-16 and NOAA-17 (Advanced Microwave Sounding Unit-B, AMSU-B), NOAA-18, NOAA-19 and European Operational Meteorological (MetOp) satellites MetOp-A, MetOp-B and Met-Op-C (Microwave Humidity Sounders, MHS) (Chen et al. 2013b). For the estimation of the satellite-based precipitation data from these microwave imagers, the Goddard Profiling Algorithm (GPROF) is applied over land and ocean (Kummerow et al. 2001), while as far as AMSUB-B and MHS sounders are concerned the Ice Water Path (IWP) technique is applied (Zhao and Weng 2002; Weng et al. 2003). Since there is a different approach estimating precipitation over land and ocean regions, TRMM 3B42 product is considered more accurate over ocean than over land. This is due to the fact that over the oceans the emissivity is lower than the emissivity of the hydrometeors that are detected from the PMW sensors, whereas over land, the opposite is true, hindering the detection of precipitation (Kubota et al. 2009; McCollum and Ferraro 2005; Sapiano and Arkin 2009). The precipitation data from IR sensors are collected by the Geosynchronous Earth Orbit Satellites (GEOS I–M) which provide better spatiotemporal coverage and more accurate precipitation estimates (Chen et al. 2013b). However, the IR-based precipitation estimates share the same limitations with the brightness temperature, corresponding to the cloud-top temperature and cloud height (Huffman and Bolvin 2015).

The 3-hourly daily precipitation estimates are produced in four stages (Huffman et al. 2007). First, for each individual Field of View (FOV), the passive microwave data are converted to precipitation estimates and each data set is averaged to 0.25° spatial grid over the ± 90 min time range. These estimates are adjusted to a “best” estimate, using a probability-matched method, according to Miller (1972). Then, IR estimates are produced using microwave calibration, after being zenith-angle corrected, averaged to the corresponding grid box’s brightness temperature and plane-fit interpolated to the corresponding 0.25° grid. Afterwards, the available microwave estimates are taken “as is”, while the missing values are completed with microwave-calibrated IR estimates. The 3-hourly merged estimates are summed on a monthly scale, creating a multi-satellite (MS) product and combined with gauge data, creating a post-real-time monthly satellite-gauge (SG) combination (3B43), following Huffman et al. (1997). The field of SG/MS ratios are estimated on 0.25° × 0.25° grid and applied to the 3-hourly data to remove bias, creating the final product (3B42). More information about the above algorithm can be found in Huffman et al. (1997).

TMPA version 6 (V6) products have been widely used in the hydrologic and related communities until 30 June 2011 (Jiang and Zipser 2010; Fang et al. 2013; Chen et al. 2013a), but many errors and uncertainties of V6 products have been reported in numerous studies (Stampoulis and Anagnostou 2012; Yong et al. 2012). Thus, a new algorithm (version 7, V7) was released in May 2012, improving the TMPA products. In V7, the enhanced TRMM Level 2 Precipitation Radar (PR) product had been used with small to moderate improvement of the previous V6 Level-2 PR product (Kirstetter et al. 2013). In addition, the 1° monthly full-monitoring gauge Global Precipitation Climatology Center (GPCC) data were used, which improved the analysis over complex terrain (Huffman et al. 2010). Furthermore, Grisat-B1 and Special Sensor Microwave Imager/Sounder (SSMI/S) infrared data were further implemented, improving the resolution and the areal coverage of V6 algorithm. More information about the V7 algorithm can be found in Huffman et al. (2010) and Huffman and Bolvin (2015).

GPM–IMERG products

The Integrated Multisatellite Retrievals for Global Precipitation Measurement (GPM) (IMERG) algorithm is based on numerous multisatellite retrievals from National Aeronautics and Space Administration (NASA) TRMM Multi-Satellite Precipitation Analysis (TMPA), NASA Precipitation Processing System (input data assembly and processing), National Oceanic and Atmospheric Administration (NOOA) Climate Prediction Center (CPC) morphing technique (CMORPH, Lagrangian time interpolation) and the Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks (PERSIANN) at the University of California (microwave calibrated IR using artificial neural networks) (Huffman et al. 2015a, b, c). GPM IMERG contains precipitation estimates from various Passive MicroWave (PMW) and IR sensors, at 0.1° × 0.1° spatial resolution, between 60° S–60° N, at several time scales (half-hourly, 3-hourly, daily, monthly).

GPM IMERG has attracted the attention of scientific community, as it generates global precipitation information at various time scales, readily available for use by researchers and decision makers. In the latest version of GPM (V07), there is a great improvement in the accuracy of the Special Sensor Microwave–Imager/Sounder (SSMIS) observations that are released as part of the GPM V07 data set (Kroodsma et al. 2021).

The precipitation estimates from PMW are calculated utilizing the 2014 version of the Goddard Profiling algorithm (GPROF2014) (Kummerow et al. 2001; Liu 2016). The merged IR data are provided by the CPC and the two estimates (PMW and IR) are used by the CMORPH–Kalman filter Lagrangian time interpolation, producing half-hourly estimates (Janowiak et al. 2001; Liu 2016). The monthly full-monitoring gauge GPCC precipitation data are used for bias correction (Schneider et al. 2015). A schematic representation of the main data flows and processing components of GPM–IMERG is presented in Fig. 2, adapted from Huffman et al. (2020).

Fig. 2
figure 2

Schematic representation of the GPM–IMERG base structure and data flow. Colored blocks represent the contribution of the participated institutions [adapted from Huffman et al. (2020)]

Full size image

The GPM IMERG provides 3 half-hourly products, namely, the IMERG Early Run (IMERG-E) with approximately a 6-h latency after observation time, the IMERG Late Run (IMERG-L) with a latency of roughly 18 h and the IMERG Final Run (IMERG-F) with almost 4 months latency after observation time (Hou et al. 2014; Huffman et al. 2015a, b, c). The IMERG-E products are available since 14th March 2015, while the IMERG-L and IMERG-F are available since 1st April 2015 and 12th March 2014, respectively. The IMERG-E and IMERG-L products are satellite-based data, while IMERG-F is a post-real time product, calibrated with the monthly full-monitoring gauge GPCC precipitation data (Wang et al. 2017). More information about the IMERG products and algorithm can be found in (Huffman et al. 2015a, b, c, 2019, 2020). It is worth noting that the various algorithms used to produce the IMERG precipitation estimates may change as remote sensing applications advance, improving the final products, whereas the monthly precipitation estimates from the Global Precipitation Climatology Project (GPCP) are considered as a more stable product, appropriate for climatological studies (Huffman et al. 2020).

According to Pradhan et al. (2022), GPM–IMERG performs better at monthly and annual time steps than at daily and sub-daily ones. In the matter of hydrological applications, the use of GPM–IMERG product has resulted in noteworthy differences in the streamflow simulation (Pradhan et al. 2022). Moreover, the most important factor is that each new version that replaces the previous one, shows significant improvement in almost every climatic condition and spatiotemporal scale, making the GPM–IMERG product a promising tool for current and future applications (Pradhan et al. 2022). The latest version 06 of GPM–IMERG product combines the early precipitation estimates, collected during the operation of the TRMM satellite (2000–2015), with the recent precipitation estimates, collected during operation of the GPM satellite (2014–present). Therefore, researchers and application developers are able to compare historical and contemporary data. In addition, they are better informed to predict the weather and climate more accurately and have the ability to distinguish between normal and extreme rain and snowfall around the world. Finally, they can develop applications to deal with present and potential disasters, spread of diseases, energy production, resource management, food security etc.

Additional remote sensing precipitation data sets—products

The Global Satellite Mapping Precipitation (GSMaP) introduces a global, hourly, gauge-adjusted precipitation rate at 0.1° using input from the GPM 3-hourly precipitation estimates from 2014 to present (Kubota et al. 2006). It is a merged PMW-IR precipitation product developed in Japan. The GSMaP “Real-time product” is provided immediately, while the other two products are provided with a latency of 3 days (“Standard product”) and 4 h (“Near-real time” product). The “Reanalysis product” which includes reprocessed historical data, are also available (Kubota et al. 2020).

Precipitation Estimation from Remote Sensing Information using Artificial Neural Network–Climate Data Record (PERSIANN–CDR) (Ashouri et al. 2015) is another precipitation data set which provides daily output at 0.25° spatial resolution almost globally (60° N–60° S), processing information from infrared (IR) satellite precipitation retrievals with the Global Precipitation Climatology Project (GPCP) gridded monthly precipitation at 2.5° (Adler et al. 2018). GPCP is satellite–gauge combined precipitation data set covering the period from 1979 to present with a latency of 2–3 months. Considering that PERSIANN–CDR enhances both temporal and spatial resolution of the GPCP data, it can be regarded as a spatiotemporal downscaling of the GPCP. PERSIANN–CDR delivers a consistent and continuous time series of precipitation suitable for assessments related to climate variability and change.

Another global precipitation data set is the Multi-Source Weighted-Ensemble Precipitation (MSWEP) (Beck et al. 2017). This data set combines ground stations data with satellite-based information and reanalysis to produce high quality precipitation data set from 1979 to near real present globally at 0.1° spatial resolution which is available at 3-hourly, daily and monthly temporal resolutions.

The Climate Hazards Group Infrared Precipitation with Stations (CHIRPS) (Funk et al. 2015) combines ground station meteorological data and satellite derived infrared Cold Cloud Duration (CCD) observations to obtain CHIRPS high resolution, i.e., 0.05°, precipitation at a daily time step for over 30 years (from early 1980s to present) with an average latency of about 3 weeks. The procedure incorporates spatial correlation structure of CCD-estimates to determine interpolation weights. Funk et al. (2015) showed how CHIRPS algorithm can be used to quantify hydrologic effects of rising air temperatures and decreasing precipitation in the Greater Horn of Africa. Finally, in their study, they showed that CHIRPS algorithm can be applied effectively for hydrologic forecasts and trend analyses in southeastern Ethiopia. Higher latitudes, however, are not covered by CHIRPS, since its spatial coverage ranges from 50° S–50° N, 180° W–180° E.

Precipitation can also be extracted from various global land data assimilation systems and reanalysis climatology data sets. Global Land Data Assimilation System (GLDAS) (Rodell et al. 2004) combines satellite observations and ground measurements. It provides estimates of many essential land variables at 3-hourly time step using land surface modeling and assimilation methods, covering the period from 2000 until today. However, the spatial resolution (i.e., 0.25°) is inadequate for the assessment of spatial variability of precipitation at local scales.

The ERA5-Land (Muñoz-Sabater et al. 2021), a global land reanalysis data set provides among many other land variables, precipitation estimates from 1950 to present, at the hourly, daily and monthly time steps at 9 km spatial resolution. It is updated daily with a latency of 5 days. Although ERA5-Land precipitation is not a satellite product, it is produced assimilating millions of observations from various data sets, e.g., precipitation radar observations, into ECMWF land surface model.

Other attempts to retrieve precipitation comprise the SM2RAIN products based on downscaled remotely sensed soil moisture combined with other satellite retrievals (Massari et al. 2020; Filippucci et al. 2022). There are, however, some limitations of the SM2RAIN precipitation mainly in complex terrains and during winter (Sharifi et al. 2019).

Downscaling methods

Accurate downscaling of precipitation remains a challenge because of the large spatial variability of precipitation which cannot be described with the spatial resolution of the SPEs. There are two main categories of downscaling methods; the statistical and the dynamical downscaling method.

Statistical downscaling approaches

Statistical downscaling methods model the statistical relationships between low resolution variables and high-resolution auxiliary variables (Tang et al. 1955; Xiaogang et al. 1969; Sharifi et al. 2019). However, a large reliable data set is required to establish an appropriate regression or other type model (Tang et al. 1955). Regarding statistical downscaling of satellite precipitation, most studies are conducted using auxiliary variables correlated with the precipitation estimates. For example, the normalized difference vegetation index (NDVI) parameter is the most widely used variable because of its high correlation with precipitation (Foody 2003; Chen et al. 2019) especially in arid and semi-arid regions, where the growth of vegetation depends mainly on precipitation. Moreover, topography effects on precipitation are well-known as orographic effects, and as a consequence the integration of the elevation factor in downscaling methods can predict better precipitation’s distribution in areas with complex terrain (Jia 2012). Nevertheless, the relationship between land surface characteristics and the precipitation (i.e., NDVI, elevation, geographical location etc.) is spatially non-stationary. Therefore, the representation of the spatial variability of precipitation by NDVI–precipitation or elevation–precipitation relationship alone is inadequate (Xu et al. 2015b). Fang et al. (2013) determined that the precipitation is also affected by the geographic location (latitude and longitude). Chen et al. (2015), introduced the use of land surface temperature (LST) parameter from the Moderate Resolution Imaging Spectroradiometer (MODIS) to improve the downscaling results for TRMM TMPA precipitation over an arid to semi-arid area. In previous studies, it has also been found (Jing et al. 2016; López López et al. 2018), that LST and slope as well as aspect had significant impact on satellite-derived precipitation downscaling. Except from the auxiliary variable, the empirical statistical relationship between satellite-derived precipitation and the used auxiliary variables can also influence downscaling results. Thus, different empirical statistical relationships have been developed in downscaling models, including univariate regression (UR) (Immerzeel et al. 2009; Duan and Bastiaanssen 2013), multivariate regression (MR) (Jia 2012; Chen et al. 2020a), and geographically weighted regression (GWR) (Chen et al. 2015; Zhao et al. 2017). However, these parametric regression-based methods are difficult to reflect the spatial inhomogeneity between precipitation and land surface characteristics (e.g., NDVI, LST, and elevation). In addition, multifractal analysis was also used as a downscaling method, consisting of a quantitative tool for the representation of the mass distribution of fractal space (Sun et al. 2022). Its main aspect is the assumption that over a region the multifractal properties of precipitation at coarse spatial resolution are the same as those at finer spatial resolution. This coarse scale parameter is assumed to consist of a heterogeneous and a homogeneous portion. The heterogeneous portion is indicated by the ensemble of the long-term properties of the precipitation, while the homogenous portion is defined by multifractals. The final rainfall estimate at finer scale is produced using a multiplicative random cascade model (Xu et al. 2015a). With the development of artificial intelligence, many machine learning algorithms, such as artificial neural network (ANN), support vector machine (SVM), random forests (RF) and deep learning (DL) have been proposed for nonlinear problems (Chaney et al. 2016; He et al. 2016; Jing et al. 2016; Chen et al. 2020a). Among the SPEs downscaling approaches, the vast majority focuses on the enhancement of the spatial resolution, while the temporal resolution for most studies remains at the daily or monthly time steps.

Statistical downscaling of SPEs was first attempted in the TRMM era. Hence, Deidda et al. (2006) utilizing remote sensing rainfall data from the Tropical Rainfall Measurement Mission–Large-Scale Biosphere Atmosphere Experiment (TRMM–LBA) land campaign, in conjunction with findings from the Tropical Ocean Global Atmosphere Coupled Ocean–Atmosphere Response Experiment (TOGA–COARE), the Global Atmospheric Research Program (GARP)–Atlantic Tropical Experiment (GATE) and the Global Learning and Observations to Benefit the Environment (GLOBE) program, studied the scaling behavior of the space–time rainfall fields and the orographic influence on them, over the Amazon Basin, for the period 10/1–28/2/1999. After performing a multifractal analysis, they found that the precipitation data were scale-invariant under self-similar transformations. In addition, they found that the orography did not play a significant role in rainfall intensity but this might be due to the fact that their study area was flat and their timeseries was short, probably concealing spatial heterogeneity and the orographic effect on precipitation fields (Purdy et al. 2001).

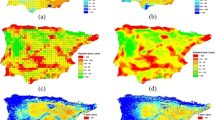
Immerzeel et al. (2009) investigated the relation between TRMM precipitation estimates and the NDVI for different spatial resolutions on the Iberian Peninsula in southern Europe, using time series from 2001 to 2007. In their study, they used the Local Moran’s Index as an indicator to reflect the spatial autocorrelation of NDVI to identify the outliers of NDVI values that they are not related to precipitation. Immerzeel et al. (2009) indicated that NDVI is a good proxy for precipitation at the annual scale and the derived relation between NDVI and precipitation was used to develop a new downscaling methodology that uses coarse scale TRMM precipitation estimates and fine scale NDVI patterns. Their downscaling procedure resulted in significant improvements in correlation, bias, and root mean square error for average annual precipitation over the whole period, as well as for individual years, i.e., a dry year (2005), and a wet year (2003). However, the temporal resolution does not allow for hydrological or natural disaster assessments, limiting thus the applicability of the acquired results.

Jia et al. (2011) developed a statistical downscaling algorithm for monthly TRMM precipitation using NDVI and Digital Elevation Model (DEM) as auxiliary variables. They applied their methodology in the Qaidam Basin in China, where they downscaled TRMM 3B43 0.25° × 0.25° precipitation fields to 1 × 1 km pixel of precipitation for each year from 1999 to 2009. Results were validated against monthly precipitation from six gauging stations, indicating r2 values ranging from 0.72 to 0.96. However, although the downscaled output performed satisfactorily also at the annual time step, the methodology is highly impacted by the accuracy of the TRMM data set.

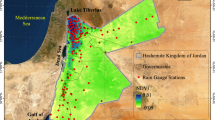
Duan and Bastiaanssen (2013) have also used NDVI as an auxiliary variable to downscale TRMM-3B43 version 7, from 0.25° to 1 km grids at the annual and monthly scales. Their approach incorporates a calibration phase, where after downscaling using site-specific non-linear relationships between annual precipitation and annually averaged NDVI, the 1-km product was calibrated using gauge data sets, based on Geographical Difference Analysis (GDA) and Geographical Ratio Analysis (GRA) (Cheema and Bastiaanssen 2012). The developed methodology was validated in different climatic conditions, i.e., in the Caspian Sea Region in Iran where arid and semi-arid conditions prevail and in the Lake Tana Basin in Ethiopia with humid climate. In their study, they proved that the Local Moran’s Index was not appropriate for identifying NDVI values that should be excluded to create the TRMM–NDVI relationship. They also proved that the whole NDVI data set (except of the negative values of NDVI in water bodies) might be used to create the relationship between TRMM and NDVI. Furthermore, they interpolated the surrounding downscaled precipitation pixels using the Inverse Distance Weight interpolator, estimating the annual precipitation over water bodies. The results of their method showed minimum difference between GRA and GDA calibration methods. Their validation study at the annual and monthly scales using rain gauge data provided satisfactory results and highlighted the improved results obtained by combining downscaling and calibration to obtain precipitation in regions with complex terrains. In addition, they indicated that NDVI is not a suitable indicator for downscaling precipitation over water bodies and ocean, while the positive relationship of NDVI and precipitation at the annual scale may not be valid in cases, where precipitation exceeds a site-specific threshold value.

Posadas et al. (2015) used a multifractal random cascade (MFRC) model to downscale daily TRMM (3B42) precipitation data from 0.25° to 0.01° over the region of Altiplano (Southern Peruvian Andes) for a period of 8 years (1999–2006). In addition, they used interpolated rainfall measurements from 19 stations across the region produced by the ANUSPLIN 4.4 package for validation purposes, in conjunction with elevation, longitude and latitude parameters (Hutchinson 1995). They concluded that the Mandelbrot–Kahane–Peyriere (PMK) function that was used for the multifractal analysis showed better performance during the wet season (November–March) than during the dry season (June–October), probably due to its sensitivity to local heterogeneity.

To overcome the problem of NDVI saturation in dense vegetation conditions and its relationship with precipitation at high precipitation regimes, Shi and Song (2015) used Enhanced Vegetation Index as an auxiliary variable to downscale TRMM 3B43 product. Thus, spatial downscaling was achieved, downscaling pixel size from 0.25° to 1 km by applying a nonparametric statistical relationship between precipitation and EVI, altitude, slope, aspect, latitude, and longitude. The methodology initially develops, at coarse scale, a nonparametric regression model using Random Forest algorithm. Next, the developed model was applied at the fine resolution to obtain fine resolution annual precipitation and the final downscaled output was produced by adding the residual terms. The downscaled annual precipitation was then calibrated with the GDA method and monthly data were produced by disaggregating the annual product by applying a simple fraction method. Therefore, the methodology of Shi and Song (2015) can be considered as an extension of the work of Duan and Bastiaanssen (2013), extending GDA for bias correction of the downscaled precipitation data set for the Tibetan Plateau from 2001 to 2012, using 91 rain gauge stations. Results indicated the improvement of monthly downscaled data especially after calibration.

Xu et al. (2015a) performed a combination of linear regression, artificial neural network (ANN) and multifractal analysis, to downscale remote sensing precipitation data (from 0.25° to 0.01°) using 16 years of monthly precipitation estimates from TRMM (TRMM 3B43), in conjunction with DEM data and rain gauge measurements from 72 stations, over South China. Their method, even though it was robust, did not improve the final, downscaled precipitation product.

The annual TRMM (3B43) data set was disaggregated from 0.25° to 1 km grids from 2000 to 2009 for North China in the work of Zheng and Zhu (2015). A hybrid approach was adopted developing a regression model with a subsequent correction method. The regression equation incorporated NDVI and continentality (CON) as auxiliary variables. To obtain monthly precipitation data the 1 km annual precipitation was disaggregated to monthly applying monthly fractions. The acquired results indicated an improvement in the agreement with data from 220 rain gauge stations.

Machine learning has been introduced in the downscaling process in the work of Jing et al. (2016), where four machine learning algorithms, i.e., classification and regression tree, k-nearest neighbors, the support vector machine, and random forests were tested for their downscaling performance for the monthly TRMM 3B43 V7 precipitation data set, from 25 to 1 km in North China. Auxiliary variables that were introduced in the models were NDVI, and DEM, longitude, latitude, daytime LST, nighttime LST, and difference of day–night land surface temperature. Results were validated against 378 rain gauges over North China during 2003, 2006 and 2009. The most important variable was discovered to be LST, whereas Random Forests algorithm was less impacted by errors with increasing precipitation.

A different downscaling approach of the TRMM 3B43 monthly precipitation was presented in Park et al. (2017), where a geostatistical approach was used incorporating rain gauge data. Initially, the coarse resolution TRMM product was downscaled to 1 km using the area to point kriging method, allowing direct comparison with rain gauge data. Then, rain gauge data were merged with the downscaled precipitation using two approaches, i.e., multivariate kriging and conditional merging, and the obtained results indicated that both methods were impacted by errors in the TRMM product. The methodology was applied in South Korea during May to October 2013, where 71 rain gauge stations were in operation. Results indicated that incorporation of a large number of rain gauge data in the TRMM did not improve the performance of the methodology. However, the situation was quite different when a small number of rain gauges is introduced in the process. In this later case the predictive ability of the downscaled product was improved considerably, indicating the effectiveness of the methodology with sparse ground monitoring points. In any case, the application of this specific methodology requires coverage of the study area with a number of rain gauges, which is not often the case, whereas the application for such a limited time period does not allow assessment of its performance in different seasons during dry and wet years.

The problem of non-stationary relationships between precipitation and land surface variables which is not considered by global and local models, that usually apply constant combinations of variables, has been addressed by Ma et al. (2017a). Therein, authors considered how the precipitation relationship with land variables, changes with the spatial scale. Thus, they developed a methodology based on Cubist algorithm to downscale monthly TMPA precipitation to 1 km spatial resolution, using NDVI, DEM and LST as auxiliary variables. Application of the methodology at the annual time step in China from 2000 to 2015 indicated that the Cubist algorithm managed to divide the data set into subsets, and they were subsequently aggregated according to their geographic similarities. The result was a division of China into subregions similar to the Chinese rainfall zones, where different relationships between precipitation and auxiliary variables were used in the downscaling process. Cubist performance was compared to Multivariate Linear Regression (MLR) using annual precipitation from 714 ground stations. Results indicated that Cubist outperforms MLR within all range of precipitation values. In their work, Ma et al. (2017a), highlighted the importance of downscaling precipitation at higher temporal resolution than the annual and the benefits of bias correction using an extended network of monitoring stations.

The methodology presented in Ma et al. (2017b) has been applied to Qinghai–Tibet Plateau. The same assumption of non-stationary relationships between precipitation and land surface characteristics was adopted and the study area was discretized into sub areas with similar land surface characteristics, such as vegetation, topography and land surface temperature. The Cubist algorithm was used to delineate the sub-regions, where the most representative variables were selected as auxiliary variables in the downscaling process. Therefore, the monthly TRMM Multisatellite Precipitation Analysis (TMPA) 3B43 Version 7 data set at 0.25° spatial resolution was downscaled to 1 km from 2000 to 2013. The results indicated an improvement of the downscaled product compared to the original TMPA, where systematic anomalies were removed. In addition, an important finding was that DEM demonstrated low correlation with precipitation over the study area.

In the study of Ma et al. (2018b), the Cubist algorithm was used again in the Qinghai–Tibet Plateau, to downscale the annual TRMM TMPA 3B43 V7 product to 1 km. The methodology used NDVI, LST and terrain characteristics extracted from DEM to acquire annual precipitation at fine resolution. The downscaled 1 km annual precipitation was subsequently calibrated to remove anomalies of the original TMPA product using the geographical ratio analysis (GRA) and ground observations. Finally, to acquire monthly precipitation records, the annual calibrated downscaled precipitation was multiplied by monthly fractions obtained by dividing the monthly TMPA estimates by the total annual precipitation, in each cell. The result of their method was the removal of anomalies in the original data set and the improvement of data quality as demonstrated comparing the downscaled monthly results with ground stations data from 2000 to 2013.

An attempt to deliver a precipitation product that could serve as forcing to hydrological models is the downscaled GPM IMERG precipitation at 1 km spatial resolution with an hourly time step (Ma et al. 2018a). It was the first downscaling approach for the GPM era precipitation, providing output at an hourly time step, although the enhancement was mainly focused on the spatial dimension, improving it from 0.1° to 1 km, whereas the temporal resolution was simply an accumulation at an hourly time step of the half-hourly initial product. Contrary to the previous work of Ma et al. (2017b), where DEM was found to have low correlation with precipitation in Qinghai–Tibet Plateau, the methodology of Ma et al. (2018a) was based solely on DEM and a new algorithm to estimate disaggregation weights, i.e., the Geographically Moving Window Weight Disaggregation Analysis. Application of the downscaling process at the Ganjiang River basin, showed that the downscaled precipitation demonstrated almost similar spatial patterns with those of original IMERG data. However, it should be pointed out that performance of the downscaling approach was assessed introducing the downscaled precipitation into the Coupled Routing and Excess Storage (CREST) model across Ganjiang River basin. CREST streamflow was then compared against streamflow monitoring data for a relatively short period, from 1 May to 30 September 2014, indicating the need for downscaling output to be validated using ground rain gauge information. Overall, the approach was interesting, as it was focused on the improvement of hydrological forecasts. However, it relied only on DEM, disregarding other variables, such as cloud properties, which are known to impact both occurrence and magnitude of precipitation.

Ma et al. (2019), demonstrated a downscaling and calibration methodology to obtain both monthly and daily downscaled precipitation from TMPA monthly (3B43) and daily (3B42). The methodology was analogous to that described in Ma et al. (2018b) as well as the study area, i.e., Qinghai–Tibet Plateau and the results indicated the same findings with those of the previously published research.

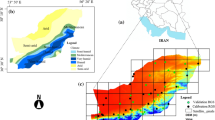
A great advance in the statistical downscaling approaches was the one followed in Sharifi et al. (2019), where, for the first time, cloud properties were used to downscale the daily GMP IMERG at the daily time step, from 0.1° to 1 km spatial resolution. In their work, cloud effective radius, cloud optical thickness, and cloud water path, were evaluated as auxiliary variables using three downscaling techniques, i.e., multiple linear regression, artificial neural networks, and spline interpolation. The results were verified by observation records of 54 rain gauges across the study area, for five heavy precipitation events, during 2015 in northeast Austria. The conclusions of their work indicated that the downscaled data set with all techniques captured the spatial pattern of precipitation better, compared to the original data set. Spline interpolation performed slightly better, whereas the residual correction improved the results. A general inference was that there cannot be a perfect agreement with the ground observations for the examined heavy precipitation events, which is expected due to the difference in spatial scale of satellite information and ground observations. A clear advantage of the adoption of cloud properties in the downscaling process is that it can also be applicable for water bodies and urban areas, where NDVI fails to serve as an auxiliary variable. A disadvantage is that cloud properties are only available during daytime. Precipitation in the study area, however, is not affected by altitude, and orographic effects should also be considered in cases of complex terrains.

A downscaling effort of the TRMM 3B43 product at the annual and monthly scales at 1 km spatial resolution over the Yangtze River Basin is presented in Chen et al. (2019) for the period 2000–2016. The downscaling was followed by a calibration process using the geographical differential analysis. Verification was conducted using monthly data from 70 ground stations operating in the study area. Both NDVI and EVI were tested for their downscaling ability and NDVI was found to perform better than EVI, while DEM was also used as auxiliary variable. After computing the annual downscaled data set, monthly values were also evaluated using monthly fractions estimated with Ordinary Kriging interpolation. The methodology was tested for GPM data as well, and in both cases, i.e., TRMM and GPM data sets, the results were satisfactory in all examined metrics.

Cloud properties have also been incorporated in the spatial downscaling of GPM IMERG half-hourly/0.1° data in the work of Ma et al. (2020). The methodology is similar to that of Sharifi et al. (2019), enhanced with the Geographically Moving Window Weight Disaggregation Analysis described in Ma et al. (2018a). The downscaled data set is provided at 0.01° × 0.01° grid, on an hourly time step for the southeast coast of China. Validation of the methodology was focused on a single typhoon event that affected the study area during 17th August 2018. Cloud properties, i.e., cloud effective radius (CER), cloud top height (CTH), cloud top temperature (CTT) and cloud optical thickness (COT), were evaluated separately and the results indicated that all variables improved the downscaled product compared to the original IMERG data set. Downscaling with CER performed better than all other variables. However, compared to gauge data, all variables performed modestly. It should be highlighted, however, than unlike the methodology described in Sharifi et al. (2019) that integrated all cloud properties in the downscaling process, in the work of Ma et al. (2020) the variables were evaluated separately. In addition, the validation was based only on a single event, while more cases including other hydroclimatic zones are certainly needed for validation purposes. Besides the great potential of cloud properties in the downscaling of satellite precipitation estimates highlighted in other works as well (Yang et al. 2019), there are difficulties while trying to downscale at a specific spatial and temporal scale. These are related to data scarcity of rainfall-related environmental variables at 0.01°/hourly scale, and also the quality of the original IMERG product that has an impact on the downscaling performance.

A comparison study was conducted in Chen et al. (2020a), where five different downscaling algorithms were evaluated for their ability to downscale GPM IMERG V06B monthly and annual precipitation from 0.1° to 1 km. The five algorithms comprised two regression methods and three machine learning methods. The comparison exercise was applied from 2001 to 2015 in the Gansu province in China, an area typical of the semi-arid-to-arid climate conditions. Five commonly used auxiliary variables were introduced in the process, namely, NDVI, LST, elevation, longitude and latitude and the acquired results were compared against ground data from 80 weather stations in the study area. Overall, machine learning models performed better compared to the regression models, with latitude having the most significant impact. Random Forest was used as the machine learning method and it outperformed the rest of the examined algorithms. The residual correction improved the results of the regression models, whereas it had only minor impact on the results of the machine learning methods. In addition, the results of the regression models had specific underestimation and overestimation spatial patterns. The work of Chen et al. (2020a) highlights the potential of Random Forest to improve precipitation data sets and expand their applicability to hydrological and other applications.

Chen et al. (2020b) performed a “temporal upscaling—spatial downscaling—temporal downscaling” technique to downscale daily TRMM–3B42 precipitation products from 0.25° to 1 km spatial resolution. They utilized NDVI, DEM and location data and performed GWR and SVR methods to investigate the relations among the parameters, over Central China, for the period 2015–2016. Then, using rain gauge data and 3 different techniques, namely, kriging with external drift (KED), conditional merging (CM) and GDA methods, produced the final precipitation, while they evaluated the performance of those methods. They concluded that their approach can improve the final precipitation product, while the KED outperformed the other approaches.

Another research using GPM IMERG (V06B, Final Run, monthly) precipitation estimates was that of Lu et al. (2020). They managed to downscale the product from 0.1° to 0.01° spatial resolution, utilizing NDVI and rain gauges data, over Tianshan Mountains, for the period May to September 2014–2018. To accomplish this, they followed the Optimum Interpolation technique (IO) (Eliassen 1954; Gandin 1965), and performed an intercomparison of downscaled IMERG data produced with GWR, spline interpolation and residual correction methods. They concluded that the IO approach improved the accuracy of the final downscaled precipitation product, while the data produced with the OI-GWR method outperformed the others. The drawback of this approach though, was that it cannot be applied in regions with no rain gauges cover.

Yan et al. (2021) performed a Random Forest method and a Data Fusion algorithm to downscale daily IMERG FF data from 0.1° to 0.01° spatial resolution. They applied their method over the Hanjiang Basin in China from 1st March 2016 to 28th February 2018, using NDVI, LST, DEM and precipitation data not only from IMERG but also from 160 regional rain gauges. They followed a three-step approach. First, they produced downscaled IMERG precipitation data utilizing NDVI, LST and DEM data and performing a Random Forest model. Then, they corrected their intermediate precipitation product using a residual correction method and finally, they performed a cokriging (CK) method to merge the downscaled rainfall with the gauge measurements. The final product was found to be more accurate than the original IMERG product, but with the limitation that their method could be implemented over regions with adequate rain gauge cover.

Two different methods were evaluated in Zhang et al. (2020a) for their downscaling ability of the TRMM3B42V7 data set from 2005 to 2010 at the monthly time step. The environmental variables used were daytime land surface temperature (LTD), slope of terrain, NDVI, altitude, longitude and latitude. The methods applied were the geographically weighted regression model and the back-propagation artificial neural networks. The results were compared with records from 27 rain gauges across the study region. The geographically weighted regression performed better than artificial neural networks, on most cases both in dry and wet seasons. A new finding is that bias correction before downscaling helps in acquiring better downscaling outputs.

The geographical weighted regression was also used in the work of Arshad et al. (2021), within an Integrated Downscaling and Calibration framework. They developed a mixed geographical weighted regression, suitable to deal with both fixed and spatially varied relationships of precipitation with environmental variables. Therefore, TRMM precipitation data from a resolution of 0.25° × 0.25° was downscaled to a high-resolution, i.e., 1 km × 1 km for the period of 2000–2018 over the Upper Indus Basin (UIB), an area with complex topography and diverse climate, at the annual, monthly and daily time scales. Many environmental variables were introduced in the process, some of those using spatially varying relationship with precipitation, i.e., actual evapotranspiration, NDVI, wind speed and cloud cover, while others were introduced with a spatially constant relationship, i.e., slope and LST. The validation of the methodology was achieved by comparing the downscaled precipitation data with data from 46 ground stations. The results of the mixed geographical weighted regression were compared to those of the ordinary geographical weighted regression, indicating that the mixed approach performs better. The calibration of the downscaled results with the recorded ground data improved the downscaled precipitation.

A geostatistical downscaling approach similar to that of Park et al. (2017) was presented in Lu et al. (2021), which was extended to downscale GPM IMERG at 1 km spatial resolution at the hourly time step. The area to point kriging was applied and a two-step correction followed, using the probability density function matching and optimum interpolation. The methodology was applied in Tianshan Mountains, China and it was validated using hourly precipitation data from 1065 automatic weather stations, indicating considerable improvement of the downscaled data set after the correction process. An advantage of the methodology is that to acquire the downscaled precipitation it does not rely on predictor’s variables. However, incorporation of ground gauge data in the correction process certainly restricts the application of the method to areas with a scarce precipitation monitoring network.

Shen and Yong (2021) followed a new approach of downscaling IMERG precipitation estimates, from 0.1° to 1° spatial resolution, using a Gradient Boosting Developing Tree (GBDT) (Friedman 2001). They used the annual IMERG FF precipitation product, in conjunction with DEM, LST and NDVI data to train and perform the GBDT, for different climatic regions over the Mainland China, for the period 2015–2018. The produced final downscaled IMERG data set, was validated using rain gauge observations. In addition, to evaluate the performance of GBDT over this complex terrain, they produced similar downscaled IMERG products using the RF and SVM methods. They concluded that the GBDT and RF methods outperform the SVM downscaling method, especially over complex regions. Furthermore, they noted that the GBDT is sensitive to the unbalanced precipitation data and that the geographical location is more important than the other surface factors.

Zhao (2021) used DEM, NDVI and precipitation data from both physical and virtual rain gauges to downscale monthly IMERG precipitation estimates, from 0.1° to 1° spatial resolution, applying a Random Forest algorithm, a residual correction technique and a kriging method. The novelty in this study, that was applied over the Heihe watershed in China for the period 2000–2021, was that he created a network of virtual rain gauges, according to the existing physical network and their topographical properties, using Shannon’s entropy and Gaussian semi-variogram methods (Shannon 1948). The precipitation amount of each site was calculated utilizing the WRF model. The downscaled IMERG precipitation estimates were produced after using a Random Forest algorithm with NDVI and DEM data (elevation, aspect, slope and relief) as covariates and applying a residual correction technique. Finally, he merged the station values with the results using a kriging method and validate them with the precipitation data from 15 virtual and 13 physical meteorological stations. He inferred that the applied residual correction improved the accuracy of the final downscaled IMERG product, while the implementation of more meteorological stations to the scheme will ameliorate the final results.

Sun et al. (2022) performed an evaluation research between three different downscaling models, namely, a Geographically Weighted Regression (GWR) model, utilizing DEM data from the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) instrument (30 m, GDEM V2) and monthly daytime LST data from MODIS instrument (MOD11A2), both onboard Terra satellite, a MultiFractal Random Cascade (MFRC) model and a combination of those two, namely, the GWR-MF model. For this purpose, they used 36 months (2015–2017) of monthly GPM IMERG FR precipitation estimates, over Hubei Province in China. For the evaluation of the models’ performance to downscale the GPM IMERG estimates from 0.1° to 0.01°, they also used precipitation data from 75 rain gauges. They concluded that the GWR–MF model performs better than the other two models, while the GWR model is more reliable than the MFRC model.

Another recent work that adopts the geographically weighted regression model, is that of Wang et al. (2022). They used topographical variables along with longitude and latitude to downscale the GSMaP, adjusted with gauge precipitation products from the 0.1° spatial resolution to 1 km, at annual, seasonal and monthly time steps from 2000 to 2020. Recent studies, such as the study of Zhou et al. (2020) showed that GSMaP–gauge precipitation data set outperforms the other GPM products at daily, monthly, and seasonal scales, and this was the rationale behind the selection of this specific product for downscaling. The study area was the Qilian Mountains, an area with complex topography. The validation that was performed using data from 27 meteorological stations in the area, showed considerable improvement of the downscaled results compared to the original GSMaP–gauge product. The accuracy of the acquired results was found to be adequate, especially at annual, spring, summer, autumn, and months from March to November. On the other hand, the lack of monitoring points in mountain areas, especially over 3000 m altitude, poses a restriction in the assessment of the downscaling performance in high altitude areas.

Zeng et al. (2022) proposed a new remote sensing downscaling precipitation technique (LPVIAL), using a newly developed Vegetation Index, based on Adaptive Lag phase (VIAL). Their technique was applied to the daily IMERG FF precipitation product, downscaling it from 0.1° to 1 km, and upscaling to 16 day temporal resolution, using NDVI, landcover type (MCD12Q1) and rain gauge data as auxiliary parameters, over Yangtze River Delta, for the period 2010–2017. Their algorithm was based on the assumption that there is a lag phase between precipitation and its response to vegetation growth. To validate their results, the final downscaled IMERG product was compared to rain gauge observations, as well as to a NDVI-only-based downscaled IMERG product. It was found that the LPVIAL accuracy was better than the NDVI approach, while the LPVIAL-based IMERG final product performed better than the NDVI-based IMERG product. A drawback of their method is that the final IMERG data set has a temporal resolution of 16 days, lower than the original product (1 day).

Table 1 summarizes the main features of the above analysis.

Table 1 Summary table of the statistical downscaling methods
Full size table

Dynamical downscaling methods

The dynamical downscaling relies on the RCMs, which process the output of GCMs or reanalysis data sets to produce climate variables at the regional or even local scales (Tang et al. 1955). Dynamical downscaling involves the use of physically based numerical models, but it is computationally demanding (Sharifi et al. 2019). There are several weather prediction systems that have the ability to assimilate precipitation data not only at a global scale, such as the European Centre for Medium-Range Weather Forecasts (ECMWF) system (Lopez and Bauer 2007; Lopez 2013), the Goddard Earth Observing System (GEOS) (Pu et al. 2002; Lin et al. 2007) and the National Centers for Environmental Prediction (NCEP) Global Forecast System (GFS) (Lien et al. 2016), but also at a regional scale as well, such as the Weather Research and Forecasting (WRF) model (Lin et al. 2015) and the Japan Meteorological Agency (JMA) system (Koizumi et al. 2005). Those systems utilize various data assimilation algorithms, such as Kalman filter (Evensen 1997), three-dimensional variational (3D-Var) (Sasaki 1958), four-dimensional variational (4D-Var) algorithms (Sasaki 1970), polynomial interpolation method (Panofsky 1949), etc. Among them, the 4D-Var assimilation algorithms are the most commonly used, since they can directly assimilate conventional and unconventional precipitation in continuous time, with better dynamic constraints (Bannister 2017). Koizumi et al. (2005) managed to successfully assimilate precipitation data from radar (1-h temporal, 20 km spatial resolution) getting improved precipitation forecasts up to 18 h ahead. Mesinger et al. (2006) reported improvements in the precipitation analysis relative to the reference monthly observations, after assimilating hourly precipitation observations into the North American Regional Reanalysis system, (3-h temporal, 32-km spatial resolution). In addition, Lopez and Bauer (2007) reported significant improvement in the short-term precipitation forecasts after assimilating NCEP precipitation into the ECMWF Integrated Forecast System.

Dynamical downscaling refers to the utilization of RCMs to simulate finer-scale physical processes conformable with the large-scale weather evolution stated from General Circulation Models (GCMs) (Giorgi et al. 2001; Schmidli et al. 2007). Specifically, the dynamical downscaling of precipitation is achieved by assimilating the precipitation data into RCMs, an approach that has received a lot of attention among the scientific community in recent years.

Lin et al. (2017) assimilated the 6-h TRMM 3B42 (v7) precipitation data, over the United States, using the 4D-Var component of the WRF Data Assimilation (WRFDA) system, in conjunction with soil moisture data from the Soil Moisture Ocean Salinity (SMOS) satellite using a WRF-Noah 1D-Var, to improve forecasting of land–atmospheric exchange and understand their relative implications. After comparing their results with data from the NCEP Stage IV precipitation data set during 1–28 July 2013, they concluded that with the assimilation of both TRMM and SMOS data, the forecast skill of precipitation was improved, by reducing the prediction biases and root-mean-square errors by 57% and 6%, respectively.

Yi et al. (2018) also applied the 4D-Var assimilation algorithm to assimilate TRMM 3B42 and GPM IMERG-F precipitation data into the WRF model, to study two heavy precipitation events in 2015 that occurred over Huaihe River Basin (HRB) in Eastern China. They evaluated the model results with in situ observations from 30 meteorological stations from the Chinese Meteorological Administration (CMA) in the HRB and with hourly merged Climate Prediction Center Morphing (CMORPH) technique data. They found that using 4D-Var assimilation method with both satellite-based precipitation data could improve WRF precipitation predictions at a time interval of approximately 12 h and that the assimilation of IMERG-F into the WRF produced better results than the assimilation of TRMM 3B42 precipitation data, since GPM data have a better capability of measuring light rain (Tang et al. 2016).

The same dynamical downscaling method (4D-Var algorithm) was used by Wang et al. (2020) examining the performance of the WRF model for forecasting heavy rainfall events over Yangze River Delta (YRD). Specifically, they examined two Tropical Cyclones (TC) events (Jondari and Rumbia) that took place in August 2018 and caused the flooding of the YRD region, using IMERG-L precipitation data. After comparing their findings with assimilating rain gauge precipitation data into the WRF model and with WRF results without assimilating observation data, they concluded that the assimilated IMERG precipitation data improved the forecast of heavy rain falls and reduced the erroneous detection rate, especially for rain rates greater than 5 mm/h.

A different approach was followed by Zhang et al. (2020b), studying three synoptic-scale convective precipitation events, during 2015–2017, over the central United States. Even though they used the 4D-Var precipitation assimilation method in WRF model with IMERG-F precipitation data, they transformed the data logarithmically before assimilating them into the WRF model. After evaluating them against the WRF predictions of non-transformed assimilated precipitation data, they found no improvement in precipitation estimations.

Another application of the 4D-Var method was made by Yi et al. (2021). They used IMERG precipitation data and assimilated them into the WRF–TOPX coupled model, to simulate a flood that occurred in August 2015, in the Wangjiaba watershed in eastern China. The comparison of their results with the precipitation data from 215 stations of Chinese Ministry of Water Resources (CMWR) revealed that the 4D-Var assimilation with the IMERG data could improve the performance of the coupled land–atmosphere WRF–TOPX model.

Discussion

Downscaling of remotely sensed precipitation has been proven to result in improved quality of the precipitation products, enhancing their ability to describe the spatial and temporal variability of precipitation. Remotely sensed precipitation estimates can be effectively downscaled using various downscaling approaches.

Regarding the statistical downscaling approaches, a variety of methods have appeared in literature, each one having its advantages and disadvantages. Statistical downscaling of remotely sensed precipitation relies on other land and climate variables, such as NDVI, EVI, LST, cloud properties, topography, longitude and latitude of finer spatial resolution. They take advantage of the better spatial representation of those variables, to produce precipitation at improved spatial scales. In this way, the inherent uncertainties of the auxiliary variables may pass to the downscaled precipitation. In addition, a statistical relationship should be established between precipitation and auxiliary variables. In some cases, certain variables, such as DEM, seem to be well-correlated with precipitation (Ma et al. 2018a), while in others, this relationship does not hold (Ma et al. 2017b), depending mainly on the area and the temporal scale of the analysis. The problem between non-stationarity of precipitation and land variables relationship seems to be well-addressed by the Cubist algorithm, although this approach has only been tested mostly at the annual time step, while monthly precipitation is acquired using monthly fractions. Those temporal resolutions are of little use for hydrological forecasts, especially for extreme events cases. Since the temporal and spatial resolution of downscaled precipitation depends on the auxiliary variables, it is difficult for downscaling approaches to utilize vegetation indices to produce higher temporal resolution output.

Geostatistical methods such as in Park et al. (2017) and Lu et al. (2021), do not rely on auxiliary variables but exploit the attributes of neighboring pixels, to obtain high resolution estimates of precipitation. Nevertheless, the performance of the method relies on the existence of network of gauging stations. The hourly downscaled precipitation acquired in Lu et al. (2021) is a great improvement compared with the monthly precipitation acquired in Park et al. (2017), indicating the potential of the methodology to provide useful input to hydrological applications and improve their forecasts. In addition, according to Park et al. (2017) that integrated rain gauge data in their data, a small number of gauge stations may improve the downscaling results considerably. Thus, the potential of the geostatistical approaches to be used even in places with small coverage of rain gauge stations is highlighted. However, further research is needed in different hydroclimatic conditions and terrains with limited rain gauges, to better investigate the performance of the geostatistical approaches. On the other hand, Lu et al. (2021), succeeded covering almost the entire study area, using numerous automatic weather stations (about 1065), allowing them to include almost all types of terrain in their study area. Another solution could be the use of active microwave sensors, which provide high-resolution precipitation data, allowing for a more detailed representation of precipitation patterns at a local scale. Thus, comparing the downscaled precipitation estimates with active microwave data we can validate the spatial representation of the downscaled products. This validation process ensures that the downscaled precipitation captures the fine-scale spatial variability and patterns of precipitation as observed by active microwave sensors. In addition, ground radars could be an alternative mean for validating downscaled precipitation during extreme weather events, such as heavy rainfall or convective storms. The high-resolution measurements provided by the ground radars allow for a detailed evaluation of the downscaled products' ability to locate storm structures and localized features associated with extreme events. By comparing the downscaled estimates with the radar observations during such events, the accuracy of the downscaled precipitation products can be assessed.

While most statistical downscaling approaches are focused on annual and monthly products, the small number of works that provide output at the daily, sub daily and even hourly time steps, constitute a great advance in downscaling, because their output is applicable in many hydrological and climate assessments. Still there is need for improvement of the temporal resolution of the downscaled product, as the main effort is to incorporate the spatial scales, losing much of the temporal information provided by the half-hourly GPM–IMERG product.

Regarding the spatial dimension, all statistical downscaling methodologies published in relevant literature provide spatial resolution up to 1 km, although most of the auxiliary variables are available at higher spatial resolutions. Results with comparison to rain gauge stations indicated that in most areas examined, the 1 km resolution sufficiently describes the spatial variability of precipitation.

Regarding the spatial dispersion of research works conducted on downscaling of satellite precipitation estimates, the vast majority of publications are focused on Asia and mostly on China. Considerably fewer works are found for Europe, Africa, and America, where the downscaling methods used were dynamical downscaling (Lin et al. 2015; Nunes 2016) or statistical downscaling methods (Retalis et al. 2017) of climatology reanalysis data sets. It is necessary to acquire results from other areas of the world, to test performance of downscaling approaches in various hydroclimatic environments with different topography (Zeng et al. 2022). One should, however, keep in mind that statistical relationships are highly area dependent, and therefore, their applicability is not foreseen at larger scales, e.g., continental or global, and this is the main disadvantage of statistical compared to the dynamical downscaling. In addition, other variables such as downscaled soil moisture may prove to be successful auxiliary variables to downscale remotely sensed precipitation estimates. SM2RAIN algorithm highlighted this potential, but the methodology still does not provide the required spatial and temporal resolution. This algorithm should be improved considerably, especially over complex terrains.

The statistical relationships cannot be regarded as stationary in time. Within the frames of a changing climate those relationships may change and should be re-evaluated. Relationships may also be different in different seasons and seasonal models could provide a better representation of precipitation seasonality.

Several correction approaches following the initial downscaling steps are found in relevant works. Residual correction provides improved results in all cases applied. A calibration process using various techniques such as the Geographical Difference Analysis or the Geographical Ratio Analysis proved beneficial as well, although their performance depends on the availability of rain gauge station data. Most researches apply calibration and bias correction on the downscaled outcome, while others apply the correction before downscaling (Zhang et al. 2020a). In any case, comparing data sets of such different spatial scales, e.g., point rain gauge data with precipitation at resolution of 10 km, does not guarantee the computation of an actual bias between the two data sets. Therefore, comparison of the downscaled fine resolution, e.g., at 1 km, with rain gauge data sets, seems much more advantageous. It should be noted that most correction and calibration processes with rain gauge data are mostly applied in lowland terrains, as there is lack of ground monitoring stations operating in mountain areas (Wang et al. 2022). It is of great importance to examine the applicability of various downscaling approaches in high altitudes but lack of ground information is a restriction for those areas.

Regarding the algorithms applied in statistical downscaling, many works use univariate or multivariate regression formulas, while others use machine learning algorithms. Even though in most works machine learning methods outperform the simple regression algorithms, there are cases where the opposite is observed (Zhang et al. 2020a). Most of the models and algorithms studied in this paper, i.e., UR model, MLR and GWR model need different prediction factors for downscaling SPEs, such as DEM, longitude, latitude, EVI, LTD, LST, NDVI etc. Thus, these different influencing factors lead to diverse effects on downscaling and variable performance. As far as the multifractal technique is concerned, even though it has been popular among the scientific community since the 1990s, it suffers from restrictions, such as the type of terrain, spatial heterogeneity, seasonal variations, availability of precipitation data and rainfall intermittency (Deidda et al. 2006). Finally, the combination of MLR and ANN method and the GMWWDA method, based on cloud properties to downscale SPEs, seems to be among the most promising methods to obtain better spatial and temporal results.

A crucial challenge for future research is latency. Currently, GPM IMERG Early Run releases precipitation data with a minimum latency of ~ 4 h, which is useful for early warning systems to operate, e.g., flood forecasts. Nevertheless, the acquisition of downscaled precipitation at reasonable spatial resolution for accurate hydrological forecasts with low latency has not yet been achieved and is unquestionably an important topic for future research.

Dynamical downscaling of TRMM and IMERG precipitation data includes their assimilation into global and regional climate models, modifying their spatial and temporal resolution, according to the model’s results (Lin et al. 2015; Nunes 2016). Among the various data assimilation methods in climate models, the most widely used is the 4D-Var method applied in WRF model, especially in the cases of extreme events (Yi et al. 2018; Wang et al. 2020). Although the computational requirements of this assimilation method are not only high but also time-consuming, the results indicate that the forecast skill of precipitation estimation from the WRF model is improved considerably (Yi et al. 2021). Unfortunately, only few studies have assimilated TRMM and IMERG precipitation data in climate models. In addition, the limited number of regions that where investigated, hinder us from evaluating these results in regions with different hydroclimatic characteristics.

To conclude, as far as spatial resolution is concerned, all examined published works obtained a spatial resolution of 1 km, while regarding the temporal resolution most works focused on the monthly time step. Only a few studies provided hourly temporal resolution (Ma et al. 2018a, 2020; Lu et al. 2021).

Precipitation downscaling methods improve not only the quality of the remotely sensed precipitation estimates but also hydrological forecasting. Nevertheless, it seems that there is no universal solution capable of downscaling satellite precipitation estimates at a global or even continental scale. Site specific approaches are, therefore, of practical importance. However, only few studies have provided output at reasonable temporal resolution, e.g., daily or sub daily. The use of cloud properties in combination with machine learning algorithms seems to be the most promising approach (Wang et al. 2022) to acquire meaningful downscaled precipitation for hydrological and other related applications and should be the focus of future research works.

Conclusions

Previous research has shown that it is essential to have high spatial and temporal resolution precipitation data for areas, where precipitation information is sparse and for regions with complex topography and various climate conditions. Several approaches have been developed to downscale the satellite-based precipitation estimates in the previous studies.

In this paper, various precipitation downscaling methodologies and models were reviewed, discretized in two main categories, i.e., the statistical and the dynamical approaches. Statistical methods include regression, multifractal, machine learning models and auxiliary environmental variables to improve the spatial resolution of SPEs. Due to their lower computational demands needed, they are much more popular than dynamical downscaling methods. In future studies, it is necessary to exploit the full potential of machine learning algorithms. In addition, the ability of many auxiliary variables to describe the spatial and temporal variability of precipitation has been investigated. All examined variables improved the downscaling of precipitation estimates, although relationships were highly dependent on the study area. Cloud properties seem to perform better both in spatial and temporal terms, although further research is needed to investigate the applicability of the methodology in various terrains and hydroclimatic conditions.

Regarding dynamical downscaling approaches, only a few studies dynamically downscaled TRMM and IMERG precipitation data using data assimilation methods. The 4D-Var assimilation method of WRF model is the most widely used in the scientific community, improving the precipitation forecast capability of the model at finer scales. Future investigations should fill in the gap of dynamical downscaling remote sensing precipitation data using more climate models, not only global but also regional, and over regions with different hydroclimatic characteristics.