Introduction

Because of its low permeability, high adsorption capacity and swelling potential (Sellin and Leupin 2013), several countries are considering the use of compacted bentonite as a barrier element in deep geological repositories for the disposal of high-level radioactive waste (Bennett and Gens 2008). To assess the long-term behaviour of these barriers, a macroscopic model of the bentonite behaviour is needed. Such models should take into account the complex internal structure of the material, which has been characterised in recent years with microstructural testing techniques. Works such as those by Monroy et al. (2010), Romero (2013), Manca et al. (2016), Sun et al. (2019), and Delage and Tessier (2021) highlight the advisability of using multiporosity macroscopic models for simulating the behaviour of compacted bentonites at engineering scale. Among these, double porosity models have experienced major advances: see, for instance, Moyne and Murad (2003), Mainka et al. (2014), Qiao et al. (2019), and the conceptual framework provided by the Barcelona Expansive Model (BExM) (Gens and Alonso 1992; Sánchez et al. 2005, 2016; Guimarães et al. 2013; Navarro et al. 2017). The BExM assumes the existence of two overlapping distinct continuous media, namely, the macro- and microstructural modelling levels, which occupy the same spatial domain. Both continua are defined as modelling tools, more in terms of functional relations rather than based on the topology of the microstructure. As proposed by Gens and Alonso (1992), the microstructural Modelling Level (m-ML) incorporates the effect on the system of the processes occurring in the spaces occupied by non-flowing water. Essentially, the microstructure is related to the space inside the aggregates formed by clay particles. The potential effect caused by changes in the aggregate geometry is modelled at the macroscopic scale by the strain increment dεm (stress and strain are expressed hereafter using the Voigt notation, with vector magnitudes given in boldface). The effect on the whole system of processes taking place in the remaining void space—the space between aggregates, where water can flow under hydrodynamic gradients—is modelled at the macroscopic scale by the Macrostructural Modelling Level (M-ML). Macrostructural voids are expected to reorganise with aggregate volume changes. For this reason, the model considers the existence at the macroscopic level of a strain increment dεM-m induced by dεm. In addition, even if aggregates were rigid bodies (to which the m-ML concept would not apply), their motion would also affect the arrangement of the space between them (macrostructural voids) generating the macroscale strains modelled in isothermal conditions by the Barcelona Basic Model (BBM) (Alonso et al. 1990): the elastic strain increment caused by stress changes, dεeM-σ, the elastic restructuration of the system due to suction changes, dεeM-s, and the plastic strains dεpM associated with the Load-Collapse surface. An additive approach is assumed, modelling the total rearrangement of the system, dεr, as

$$d{{\varvec{\upvarepsilon}}}_{{\text{r}}} = d{{\varvec{\upvarepsilon}}}^{{\text{e}}}_{{{\text{M-}}\upsigma }} + d{{\varvec{\upvarepsilon}}}^{{\text{e}}}_{{\text{M-s}}} + d{{\varvec{\upvarepsilon}}}^{{\text{p}}}_{{\text{M}}} + d{{\varvec{\upvarepsilon}}}_{{\text{M-m}}} + d{{\varvec{\upvarepsilon}}}_{{\text{m}}} .$$
(1)

In problems with constant temperature and gas pressure PG, if salinity can also be neglected, the constitutive framework allows for computing the values of dεeM-s, dεpM, dεM-m, and dεm from dPL and dem, where PL (liquid pressure) and em (microstructural void ratio: volume of intra-aggregate voids per volume of minerals) are the state variables of the macro- and microstructural water mass balance equations, respectively (Navarro et al. 2019). On the other hand, the state variable of the mechanical problem in displacement-based finite-element approaches is the displacement field of the solid skeleton u by which the Green–Lagrange strain is

$${{\varvec{\upvarepsilon}}}_{{\text{u}}} = \frac{1}{2}\left[ {\left( {\nabla {\mathbf{u}}} \right)^{{\text{t}}} + \nabla {\mathbf{u}} + \left( {\nabla {\mathbf{u}}} \right)^{{\text{t}}} \cdot \nabla {\mathbf{u}}} \right],$$
(2)

where “∇” is the material gradient, and the transpose operator is denoted by superscript “t”. The consistency of the strains considered at both modelling levels, dεr, and the strain estimated by the mechanical model, dεu, implies that

$$d{{\varvec{\upvarepsilon}}}_{{\text{r}}} = d{{\varvec{\upvarepsilon}}}_{{\text{u}}} ,$$
(3)

and dεeM-σ is thereby computed as

$$d{{\varvec{\upvarepsilon}}}^{{\text{e}}}_{{{\text{M-}}\upsigma }} = d{{\varvec{\upvarepsilon}}}_{{\text{u}}} - \left( {d{{\varvec{\upvarepsilon}}}^{{\text{e}}}_{{\text{M-s}}} + d{{\varvec{\upvarepsilon}}}^{{\text{p}}}_{{\text{M}}} + d{{\varvec{\upvarepsilon}}}_{{\text{M-m}}} + d{{\varvec{\upvarepsilon}}}_{{\text{m}}} } \right).$$
(4)

Then, dεeM-σ can be interpreted as the “gap” between the predicted arrangement by the mechanical module (dεu) and the estimated rearrangement by the constitutive formulation of the macro- and microstructural processes which are not related to the elastic strain induced by stresses (dεeM-s + dεpM + dεM-m + dεm). Assuming a model for the bulk modulus K and shear modulus G, the gap increment (dεeM-σ) is used to track the evolution of the stress state of the system. This computational scheme is applied in numerous double porosity models (Sánchez et al. 2005, 2016; Guimarães et al. 2013; Navarro et al. 2017). However, its validity must be questioned when the macrostructural void ratio eM (volume of inter-aggregate voids per volume of minerals) becomes small and the mechanical effect of the M-ML is negligible.

The functional “exhaustion” of the M-ML may originate for various reasons, amongst which two significant cases arise. First, as a result of mechanical loading, such as in a squeezing test, when eM is notably reduced as compared to the microstructural void ratio em. Second, in swelling pressure tests, in which em increases under isochoric conditions thus decreasing eM. Navarro et al. (2021) recently proposed a simulation strategy based on the assumption of the potential growth of K for eM below a certain reference value. Although results were satisfactory in the analysed cases, the definition of K is not physically based, thus hampering the extrapolation and applicability of the approach. To circumvent this issue, the objective of the present study is to analyse in more detail the evolution of strains in bentonites for a decreasing eM, proposing a more consistent physically based formulation. Such consistence was experimentally contrasted with a series of tests designed for this purpose. The good results obtained support the formulation. Moreover, it was implemented into a numerical model for a thorough evaluation. Satisfactory numerical results were obtained without prior parameter estimation, but using material parameters from the literature, emphasising, in consequence, the simulation capability of the proposed formulation.

Conceptual model

As eM becomes very low, the system deformability is increasingly associated with changes in em. Therefore, the mechanical functionality of the M-ML is lost. The loss of some functional capacity for one of the modelling levels (loss of effect on the overall behaviour of the system) is not a novel hypothesis. All models disregarding microstructural flow are in fact assigning null hydraulic functionality to the m-ML. Yet, neglecting the hydraulic functionality in the m-ML does not deny its existence, nor its role in the stress–strain behaviour of the system, as clearly expressed in Eq. [1]. Analogously, accepting that the M-ML is irrelevant to the stress–strain behaviour of the bentonite for small eM values does not yield the assumption of a null macrostructural hydraulic functionality. As in Navarro et al. (2021), a double porosity framework is considered, assuming that a residual macroporosity is always maintained through which some advective flow takes place, although flow through residual macroporosity is likely to be small. With keeping a double porosity model, in the proper conditions for eM to increase, the mechanical functionality of the M-ML is to be reactivated, recovering the modelling reasoning behind Eq. [1].

In this conceptual framework, the changes of em are associated with mass exchange between both modelling levels (modelled as in Navarro et al. 2021). The formulation by Coussy (2007) is then adopted, posing the Clausius–Duhem equation as

$${{\varvec{\upsigma}}}_{{\text{m*}}} \cdot d{{\varvec{\upvarepsilon}}}_{{\text{m*}}} {\mathbf{ + }}\left( {\mu_{{\text{m}}} - \mu_{{\text{M}}} } \right)\,dn - dF \ge 0,$$
(5)

where dεm* is the strain of the system (induced by only the m-ML), μm and μM are the chemical potentials of the water in the m-ML and M-ML, respectively, dn defines the increase of molar content of the m-ML (em increase is taken as positive), and dF is the variation of free energy. The system deformability being governed by the m-ML does not directly equate the strain to dεm. This is the strain undergone by the system as a result of the change in volume of the aggregates when there are voids between them. When these voids are close to zero, the induced strains are likely to be different. For this reason, a strain increment dεm* potentially different from dεm is considered in Eq. [5]. Assuming a saturated microstructure, and according to the proposal of Houslby and Puzrin (2000), strain work is computed using the effective stress σm* given by

$${{\varvec{\upsigma}}}_{{\text{m*}}} {\mathbf{ = \sigma }}_{{{\text{TOT}}}} - {\mathbf{m}} \cdot P_{{\text{m*}}} ,$$
(6)

where σTOT is the vector of total stresses, m is the vector storing the identity matrix in the dimensions of stress in Voigt’s notation, and Pm* is a reference pressure. To define this reference pressure, Eq. [5] is expressed in isotropic conditions:

$$p_{{\text{m*}}} \cdot d\varepsilon_{{\text{V-m*}}} {\mathbf{ + }}\left( {\mu_{{\text{m}}} - \mu_{{\text{M}}} } \right)\,dn - dF \ge 0,$$
(7)

where pm* and dεV-m* are the respective volumetric components of σm* and dεm*, and pm* = pTOT – Pm*. A Lagrangian formulation is adopted, in which dF is the free energy per solid unit volume associated with a material volume, and the Clausius–Duhem equation becomes

$$- \;\left( {p_{{\text{m*}}} + \rho_{{\text{W}}} \left( {\mu_{{\text{M}}} - \mu_{{\text{m}}} } \right)} \right)\,de_{{\text{m}}} - \;dF \ge 0,$$
(8)

where ρW is the water density. Therefore, from an energy point of view, pm* + ρW (μM − μm) and em can be seen as conjugate magnitudes, so pm* + ρW (μM − μm) can be interpreted as the constitutive stress for em. Navarro et al. (2018) identified this role to be played by the thermodynamic swelling pressure π and thus

$$p_{{\text{m*}}} + \rho_{{\text{W}}} \left( {\mu_{{\text{M}}} - \mu_{{\text{m}}} } \right) = \pi ,$$
(9)

is assumed. Defining the chemical potential of the macrostructure (Edlefsen and Anderson 1943) as

$$\mu_{{\text{M}}} = \mu_{{{\text{VO}}}} - \frac{{s_{{\text{M}}} + s_{{{\text{MO}}}} }}{{\rho_{{\text{W}}} }},$$
(10)

that of the microstructure by (Anderson and Low 1957; Karnland et al. 2005)

$$\mu_{{\text{m}}} = \mu_{{{\text{VO}}}} + \frac{{p - \pi - \Delta s_{{{\text{mNCC}}}} }}{{\rho_{{\text{W}}} }},$$
(11)

and from Eqs. [9–11], it results

$$P_{{\text{m*}}} = P_{{\text{L}}} - \left( {s_{{{\text{MO}}}} - \Delta s_{{{\text{mNCC}}}} } \right),$$
(12)

where PL and sMO are, respectively, the pressure and osmotic suction of the aqueous solution remaining in the M-ML. Suction ∆smNCC expresses the decrease in chemical potential, in units of energy per unit volume, of the microstructural water as a result of the existence of ions in excess over its cation exchange capacity, i.e., “extra” salinity due to non-charge-compensating ions. In Eqs. [10] and [11], μVO is the chemical potential of free pure water, sM (Eq. [10]) is the macrostructural suction taken equal to the capillary suction sM = PG – PL (with PG equal to the atmospheric pressure), and p = pTOT − PG (Eq. [11]) is the net mean pressure.

With Pm* known, σm* is obtained with Eq. [6] and dεm* is defined by

$$d{{\varvec{\upvarepsilon}}}_{{\text{m*}}} = {\mathbf{C}}_{{\text{m*}}} \cdot d{{\varvec{\upsigma}}}_{{\text{m*}}} ,$$
(13)

where the compliance matrix Cm* is the inverse of the stiffness matrix Dm* expressed as

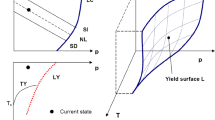
$${\mathbf{D}}_{{\text{m*}}} = \left[ {\begin{array}{*{20}c} {K_{{\text{m*}}} } & 0 \\ 0 & {3G{}_{{\text{m*}}}} \\ \end{array} } \right]{ ,}$$
(14)

where the bulk modulus Km* (volumetric compressibility of the medium), defined by the state function in Fig. 1 that relates em and π (Navarro et al. 2017), is obtained as

$$K_{{\text{m*}}} = \frac{d\pi }{{d\varepsilon_{{\text{V-m*}}} }} = \frac{d\pi }{{de_{{\text{m}}} }}\frac{{de_{{\text{m}}} }}{{d\varepsilon_{{\text{V-m*}}} }} = - \left( {1 + e_{{\text{O}}} } \right)\frac{d\pi }{{de_{{\text{m}}} }},$$
(15)

being eO the initial value of the total void ratio (e = em + eM: volume of voids per mineral volume), and the shear modulus is computed with the general expression:

$$G_{{\text{m*}}} = \frac{{3\;\left( {1 - 2\,\nu_{{\text{m*}}} } \right)}}{{2\;\left( {1 + \nu_{{\text{m*}}} } \right)}}K_{{\text{m*}}} .$$
(16)
Fig. 1
figure 1

State surface em–π (adapted from Navarro et al. 2017)

Full size image

For the sake of simplicity, Poisson’s ratio νm* is taken equal to the value ν used to obtain the shear modulus associated with the strain dεeM-σ. The resulting formulation does not require any additional model parameters, since both ν and the em–π law are already used when Eq. [1] is valid. Conventionally, this will be accepted when the macrostructural void ratio is greater than a threshold value eM-T, assuming the mechanical functionality of the M-ML to vanish for eM = eM-R (residual value). A smooth transition for this process, with the subsequent activation of Eq. [13], is ensured by the transition function iM, by means of the expression:

$$d{{\varvec{\upvarepsilon}}}_{{\text{r}}} = i_{{\text{M}}} \;\left( {d{{\varvec{\upvarepsilon}}}^{{\text{e}}}_{{{\text{M}}-\upsigma }} + d{{\varvec{\upvarepsilon}}}^{{\text{p}}}_{{\text{M}}} + d{{\varvec{\upvarepsilon}}}^{{\text{e}}}_{{\text{M-s}}} + d{{\varvec{\upvarepsilon}}}_{{\text{M-m}}} + d{{\varvec{\upvarepsilon}}}_{{\text{m}}} } \right) + \left( {1 - i_{{\text{M}}} } \right)\;d{{\varvec{\upvarepsilon}}}_{{\text{m*}}} ,$$
(17)

where iM is defined as a first approximation by a cubic Bézier curve, equal to 1 for eM ≥ eM-T and to 0 for eM ≤ eM-R. Tentative values, based on the simulation of several confined swelling and squeezing tests, of eM-T = 0.02 and eM-min2 = eM-R/10 are considered in this work. However, the selection of these parameters will be made more accurately with broader experience in the application of the model.

As pointed out in the Introduction, the strains associated with the M-ML for eM ≥ eM-R are modelled with the BBM (using the formulation by Alonso et al. 2011), which relates dεeM-σ and the increment of net stress dσ by

$$d{{\varvec{\upvarepsilon}}}^{{\text{e}}}_{{{\text{M-}}\sigma }} = {\mathbf{C}}_{{\text{M}}} \cdot d{{\varvec{\upsigma}}},$$
(18)

where the compliance matrix CM is the inverse of the macrostructural stiffness matrix DM, in which the macrostructural bulk modulus is defined as

$$K_{{\text{M}}} = \frac{{\left( {1 + e_{{\text{O}}} } \right)\;p}}{{\kappa_{{\text{M}}} }},$$
(19)

where κM is the macrostructural elastic compressibility parameter for changes in stress. Similarly, to the case of Eq. [16], the macrostructural shear modulus GM used in DM is calculated by

$$G_{{\text{M}}} = \frac{{3\;\left( {1 - 2\,\nu } \right)}}{{2\;\left( {1 + \nu } \right)}}K_{{\text{M}}} ,$$
(20)

Then, by introducing Eqs. [13] and [18] into Eq. [17], and considering the consistency condition in Eq. [3], dσ is defined by (see Appendix 1)

$$d{{\varvec{\upsigma}}} = {\mathbf{D}} \cdot \left( {d{{\varvec{\upvarepsilon}}}_{{\text{u}}} - i_{{\text{M}}} \cdot d{{\varvec{\upvarepsilon}}}_{{\text{M*}}} } \right) + \left( {1 - i_{{\text{M}}} } \right)dP{}_{{\text{F}}} \cdot {\mathbf{m}},$$
(21)

where

$$\begin{gathered} ({\text{a}})\quad d{{\varvec{\upvarepsilon}}}_{{\text{M*}}} = d{{\varvec{\upvarepsilon}}}^{{\text{p}}}_{{\text{M}}} + d{{\varvec{\upvarepsilon}}}^{{\text{e}}}_{{\text{M-s}}} + d{{\varvec{\upvarepsilon}}}_{{\text{M-m}}} + d{{\varvec{\upvarepsilon}}}_{{\text{m}}} \hfill \\ ({\text{b}})\quad dP_{{\text{F}}} = \frac{K}{{K_{{\text{m*}}} }}\left( {dP_{{\text{m*}}} - dP_{{\text{G}}} } \right) \hfill \\ ({\text{c}})\quad {\mathbf{D}} = \left[ {\begin{array}{*{20}c} {{1 \mathord{\left/ {\vphantom {1 K}} \right. \kern-0pt} K}} & 0 \\ 0 & {{1 \mathord{\left/ {\vphantom {1 {\left( {3G} \right)}}} \right. \kern-0pt} {\left( {3G} \right)}}} \\ \end{array} } \right]\;;\;\frac{1}{K} = \frac{{1 - i_{{\text{M}}} }}{{K_{{\text{m*}}} }} + \frac{{i_{{\text{M}}} }}{{K_{{\text{M}}} }}\;;\;G = \frac{{3\;\left( {1 - 2\,\nu } \right)}}{{2\;\left( {1 + \nu } \right)}}K, \hfill \\ \end{gathered}$$
(22)

Equation [21] summarises the formulation proposed in this work. It allows to integrate net stresses with a smooth transition from stress states being fundamentally controlled by the M-ML (iM = 1) to being governed by the m-ML (iM = 0). Equation [22] (b) defines, in turn, the change of reference pressure from PG (iM = 1) to Pm* (iM = 0). Once iM is assumed, the model does not introduce parameters additional to those used in double porosity models, applied when eM ≥ eM-T.

Model implementation

For the formulation described in Sect. “Conceptual model” to be operative, it must be implemented in a numerical module based on a double porosity approach, conceptual framework of reference. A displacement-based finite-element module is assumed, with net stress and macrostructural suction as constitutive stresses of the macrostructure (Houlsby 1997). Net stress is then originally determined from Eq. [18] by time integration of

$$d{{\varvec{\upsigma}}} = {\mathbf{D}}_{{\text{M}}} \cdot d{{\varvec{\upvarepsilon}}}^{{\text{e}}}_{{{\text{M-}}\sigma }} = {\mathbf{D}}_{{\text{M}}} \cdot \left( {d{{\varvec{\upvarepsilon}}}_{{\text{u}}} - d{{\varvec{\upvarepsilon}}}_{{\text{M*}}} } \right),$$
(23)

where dεM* is defined by Eq. [22] (a). As indicated by Eq. [21], the implementation of the proposed formulation will consist of the substitution of DM by D, the introduction of iM (function of eM) multiplying dεM*, and the addition to the stress vector of (1-iM) PF·m. These are minor, easily programmable modifications that give in return a powerful tool for modelling the effect on the mechanical behaviour of the system with a progressive reduction of eM.

The hydraulic effect can also be easily introduced. Assuming the M-ML to maintain its functionality, a transition function such as iM is not necessary. Considering the large reduction of eM, it is nonetheless advisable to incorporate the effect of the variation of macrostructural porosity on flow. This is usually included in the definition of intrinsic permeability, typically expressed as a function of macrostructural porosity (e.g., in Gens et al. 2011). Besides, the foreseeable effect of large eM variations on the macrostructural water retention properties is to be modelled by an approach such as the one proposed by De la Morena et al. (2021), Appendix 2, used in this work. Interesting complementary information on the retention properties of bentonite-based materials can be found in Fattah and Al-Lami (2016) and Fattah et al. (2017).

The retention model, together with Eqs. [21] and [22], were implemented by modifying the finite-element code used in Navarro et al. (2021), which adopts the algorithms and the hydro-mechanical formulation in Navarro et al. (2019). The latter work describes in detail the field equations used to model the flow as well as the formulation of the state functions that determine the strains defining dεM*. However, a brief description of these equations is given in Appendices 3 and 4. Based on this conceptual model, the numerical model was developed using the Comsol Multiphysics (COMSOL AB 2018) implementation platform, a software for solving partial differential equations by applying the Galerkin finite-element method with Lagrange multipliers. While the software offers pre-built modules, it also incorporates the "Multiphysics" capability to build modules in which the state variables can be selected, the state functions to be used can be defined, and the functional structure of the differential equations to be solved can be determined. This was the implementation strategy followed, so that the numerical model developed is adapted exactly to the formulation described in the previous section. The tayloring of the numerical formulation to the conceptual model improves its computational efficiency. Moreover, Comsol Multiphysics applies automatic symbolic differentiation techniques to obtain a high quality definition of the system iteration matrix, also contributing to improve the numerical performance of the solver. However, the application of symbolic differentiation requires that the functional dependence of the state functions used in the formulation be done carefully. Otherwise, Comsol Multiphysics is not able to apply the chain rule, cannot define the derivatives, and the calculation cannot be performed. In fact, if there are functions in which there is an implicit dependence, they must be defined as state variables of the problem to calculate their derivatives. This is the case, for example, with stresses in non-linear elastic or elastoplastic models. In this situation, as described in Navarro et al. (2014), a mixed method should be applied. However, once these problems are solved, the versatility and efficiency of the numerical tool is remarkable. The results presented in Sect. “Results and discussion” have been obtained with it.

Model inspection: experimental data

If the proposed formulation is accurate, the deformational behaviour of bentonite when eM is reduced is expected to be controlled by the state surface in Fig. 1. Thus, it is of interest to carry out laboratory tests in which the porosity decreases to contrast this hypothesis. To this end, ensuring maximum homogeneity of the specimen throughout the procedure, compression tests were carried out in which vertical loads were increasingly applied to bentonite samples in radial confinement conditions. Several samples at different initial dry densities and water contents were tested. For samples preparation, the bentonite was oven-dried, adding afterwards the necessary amount of deionised water to reach the target water contents. Sample homogeneity was ensured by enclosing the wetted soil in impermeable plastic film for 2 weeks under laboratory conditions, with a temperature of 23 ± 2 °C and a relative humidity of 40 ± 5%. The homogenised material was then statically compacted (see the compaction pressures in Table 1) into samples with a diameter of 36 mm and 5 mm high, using polyphenylene sulphide (PPS) ring moulds of thickness 31.85 mm to prevent radial deformation. After compaction, suction was measured using a chilled-mirror dew-point psychrometer (METER 2021), with an accuracy of ± 0.05 MPa from 0 to 5 MPa and 1% from 5 to 300 MPa of suction. Samples were then introduced into the compression equipment, based on rings of the same properties as the compaction moulds. A vertical load rate of 2.5 MPa/h was applied for 16 h, holding the final 40 MPa load for 8 h more. During the experiments, vertical displacement was measured independently from the readings of the press using a digital dial indicator with an accuracy of 2.5 µm (Hoffmann 2021). Suctions were measured again at the end of the test. The obtained results are shown in Table 1. The same Wyoming bentonite tested in Navarro et al. (2017) was used for this study, similar to the Be-Wy-BT007-1-Sa-R bentonite characterised by Kiviranta and Kumpulainen (2011), the main properties of which are summarised in Table 2.

Table 1 Compression tests
Full size table
Table 2 Characteristic properties of the analysed soils
Full size table

The experimental data in Table 1 corresponds to each sample as a whole. However, the analysis of results regarding their spatially distributed behaviour is also of interest, although information of this kind is scarce. In that sense, the hydration tests reported by Massat et al. (2016) constitute a valuable contribution, as it reports in a distributed (for different points of the sample) and continuous (for different times) way the variation of porosity. A cylindrical sample of 10 mm in diameter and height, with an average dry density of 1.47 g/cm3 and initial water content of 6.7%, was subjected to water injection at a pressure of 50 kPa through its bottom base. Null flow through the remaining boundaries was reported. The sample was kept in isochoric conditions, and the vertical swelling pressure was measured. The cell was adapted to perform X-ray microtomography (Massat et al. 2016), giving images of voxel size 5 mm, further processed using image analysis techniques to estimate the evolution of the macrostructural porosity distribution in the sample. Amongst the tests reported, this work will analyse the results obtained under low salinity conditions (0.4 mM) (Massat et al. 2016), focusing on the process of e reduction without modelling the effect of salinity. Table 2 summarises the main characteristics of the Kunipia-G montmorillonite used in Massat et al. (2016).

Results and discussion

Delage and Tessier (2021) evidenced that compression induces the progressive reduction of the larger voids. With larger voids present, the voids in the m-ML remain practically unaltered, thus em remaining constant, and consequently π remains constant as well. This way, the path 1 → 2 in Fig. 2 will be initially followed in the tests, figure that is the conceptual scheme of the tests in the e–π space. If equilibrium is assumed at the beginning of the test, μm = μM will be met at that point, and from Eqs. [10] and [11]:

$$\pi = p + s_{{\text{M}}} + \left( {s_{{{\text{MO}}}} - \Delta s_{{{\text{mNCC}}}} } \right).$$
(24)
Fig. 2
figure 2

Diagram of paths 1 → 2 → 3 followed in Table 1 tests within space e–π over the reference state surface em–π (grey line)

Full size image

Since the initial load is null and the tests are perfomed under reduced salinity conditions, π can be taken equal to the initial suction in Table 1, and em-1 (initial microstructural void ratio, constant along 1 → 2) can be computed from the state surface in Fig. 1. In addition, since point 2 lies on the state surface em–π, a significant change in the bentonite deformability is expected upon reaching that point. Further loading, after exhaustion of macropores, would follow path 2 → 3. Figure 3a represents the evolution of vertical displacement δ, positive in the loading direction, with increasing vertical pressure σz. A change in slope is observed after initial loading, but δ remains constant afterwards instead of increasing with a new slope (which would be presumably smaller due to soil rigidisation along 2 → 3 with eM ≈ 0). This situation remains for the tests in Fig. 3b, whereas the tests in Fig. 3c show a second δ increase after the plateau, albeit with a reduced slope compared to the initial slope. The values of δP on the plateau (Table 1) are used in the calculation of the corresponding void ratio ep, which are practically equivalent to em-1, as can be seen in Fig. 4. All tests are represented in Fig. 4, although many of the points overlap. For the tests in Fig. 3b, suction at the end of the experiments was also very similar to the initial values, see Table 1. It is hence reasonable to assume that the plateau identifies point 2 in Fig. 2.

Fig. 3
figure 3

Evolution of the vertical displacement δ with increasing vertical pressure σz. a All of the tests in Table 1. b Tests in which δ stabilises after reaching a plateau. c Tests experiencing a second increase of δ

Full size image
Fig. 4
figure 4

Comparison of ep vs em-1

Full size image

After reaching point 2, the values of σz are those corresponding to the plateau in Fig. 3, and, assuming a coefficient of earth pressure at rest of

$$k_{{\text{O}}} = \frac{\nu }{1 - \nu },$$
(25)

the increase in net mean stress on the plateau can be estimated, where because δ is constant, e, and thus em, will not change. Since em in 2 is the same as in 1, according to Fig. 1, the microstructural effective stress π will also be the same. Excluding the effect of salinity, the variation of sM is defined by p, π, and Eq. [24]. Even taking into account the simplification introduced by Eq. [25], these calculations show very high suction values on the plateau for the results in Fig. 3b. The bentonite is initially in dry conditions, and even though the increase in p leads to a reduction of sM as a consequence of a decreasing eM, suction is still high. There is no drainage, and when eM ≈ 0 is reached (point 2), the system shows an isochoric “undrained” behaviour. Contrarily, the tests in Fig. 3 c have larger initial water contents and, after some loading, suction is reduced enough for the bentonite to start draining and deforming, originating the second stage of increase in vertical displacement. In it, deformability is governed by the em reduction and the behaviour is stiffer than in the first increase, where deformability is associated with the reduction of eM.

For the tests in Fig. 3c, the value of δ allows to define the reduction of em from point 2 onwards. Since em on 2 is equal to em-1, the change of em from there determines its total value, and then, using Fig. 1, the thermodynamic swelling pressure can be obtained in 2 → 3. Particularly, the values of em-3 and π3 at the end of the experiment, before dismantling the sample from the testing equipment, can be calculated (Table 1). If the operation is swiftly carried out and the sample suction sM3 is measured right after the dismantlement, according to Eq. [24] it must be equal to π3 for p = 0 after unloading. Figure 5 confirms the good correlation between π3 and sM3, corroborating the conceptual model sketched in Fig. 2 and thus underpinning the formulation proposed in this work.

Fig. 5
figure 5

Correlation between π3 and sM3

Full size image

Once the conceptual consistency of the formulation is confirmed, it is of interest to improve the characterisation of the simulation capability of the proposed numerical model. Tests numbers #1, #10, #16, and #18 were chosen as representative study cases. As noted above, the Wyoming bentonite used in the experiments presented is the same used in Navarro et al. (2017), Navarro et al. (2016) and Sane et al. (2013).

Therefore, except for the net mean preconsolidation stress at zero suction, the mechanical parameters estimated by Navarro et al. (2016) from the tests of Sane et al. (2013) have been used, see Table 3. Both the preconsolidation stress and the permeability parameters have been taken as those identified by Navarro et al. (2017) when analysing the experimental results of Sane et al. (2013) with an improved swelling model with respect to the one used in Navarro et al. (2016). Table 3 also includes the micro–macro-mass exchange parameters taken from Navarro et al. (2016) and the M-ML retention properties for a Wyoming bentonite from De la Morena et al. (2021). Regarding the material characterisation, the em–π state surface in Fig. 1 was used (Navarro et al. 2017).

Table 3 Mechanical and hydraulic parameters used in the simulations
Full size table

Free vertical and null radial displacements (“roller” boundary condition in the mechanical problem) were assumed on the lateral boundaries of the sample for the simulations. Furthermore, the bottom boundary displacements were also constrained vertically, and, in accordance with the test, a load increment of 2.5 MPa/h was applied on the top boundary for the first 16 h of testing, keeping the final 40 MPa load for the remaining 8 h of simulation (test duration of 24 h). For the hydraulic simulation, the lateral boundaries were considered impervious, while seepage boundary conditions (Neuman and Witherspoon 1970) were imposed at the top and bottom boundaries. Initial conditions were taken consistently with the dry density and water content values in Table 1.

Figure 6 depicts the experimental and numerical results of the evolution of δ vs σz. Notable fit is observed given that the parameters used were directly taken from previous works without any kind of parameter estimation (the parameters used are completely independent of the test simulated). Not only the transition around point 2 in Fig. 3 is correctly simulated, but also the soil behaviour along path 2 → 3 is reasonably reproduced. In this regard, Fig. 7 shows the paths followed in the e–π space, and Fig. 8 represents the time evolution of e, eM, and em (where, for the sake of clarity, only the results of simulations #1 and #18 are shown). Figures 7 and 8 show modelling results on points at ¼, ½, and ¾ of the sample height, namely, PA (1.25 mm), PB (2.50 mm), and PC (3.75 mm), although the values obtained at different heights are indistinguishable as they overlap. A sub-vertical path in e–π is observed (Fig. 7), while M-ML is relevant (see Fig. 8: eM > eM-T), the system behaviour smoothly shifting to being controlled by the em–π state surface. Interestingly, in the no-flow or extremely reduced flow conditions of the problem, a homogeneous response of the sample is found, as implicitly assumed in Figs. 4 and 5, and for the calculated values in Table 1.

Fig. 6
figure 6

Comparison between experimental values (markers) and the numerical model results (solid lines) of the evolution of δ vs σz

Full size image
Fig. 7
figure 7

Numerical simulation of paths 1 → 2 → 3 within the e–π space of points PA, PB, and PC. The numbering in first place in the legend indicates the simulated tests from Table 1. For clarity, not all the points obtained in the simulations are represented with a marker

Full size image
Fig. 8
figure 8

Numerical simulation of the time evolution of e, eM, and em of points PA, PB, and PC. The numbering in first place in the legend indicates the simulated tests from Table 1. For clarity, not all the points obtained in the simulations are represented with a marker

Full size image

Finally, the evaluation of the conceptual and numerical formulations was completed with the simulation of the hydration test by Massat et al. (2016), described in Sect. “Model inspection: experimental data”. This is a very demanding simulation involving the characterization of the spatially and temporally distributed soil behaviour. A no normal displacement mechanical boundary condition is imposed on all boundaries. Furthermore, top and lateral impervious boundaries were considered, applying (as in the test) a 50 kPa pressure on the bottom boundary of the cylindric sample. A homogeneous initial water content of 6.7% was taken, and a linear vertical variation of the dry density idealising the variation of macrostructural initial porosity identified in Massat et al. (2016) was adopted, as shown in Fig. 9. This figure shows the evolution of the vertical profile of macrostructural porosity with time, comparing experimental values with the obtained results in this work and in Navarro et al. (2021), both using the mechanical and permeability properties in Table 3. Water retention properties (van Genuchten 1980) and the state surface em–π were all derived from experimental results on Kunipia-G montmorillonite (Sato 2008). Please refer to Navarro et al. (2021) for further details. Both models produce comparable goodness of fit to the experimental data. Therefore, even with fewer parameters (the maximum stiffness of the system is not introduced independently), the new formulation is able to satisfactorily reproduce the test by Massat et al. (2016), which reinforces the validity of the proposed formulation.

Fig. 9
figure 9

Evolution of macrostructural porosity in the test analysed from Massat et al. (2016). Markers: experimental values (exp). Solid lines: results obtained with the proposed model (m2). Dashed lines: results from Navarro et al. (2021) (m1). IC: initial condition

Full size image

Conclusions

A formulation has been proposed that models the effect of interaggregate space reduction on the hydro-mechanical behaviour of compacted bentonites. This formulation assumes a macroscopic model of bentonite based on a double porosity approach. In it, the effects on the system of processes taking place in the intra-aggregate space are modelled by an equivalent continuous medium, the microstructure. In this work, it is labelled as the “microstructural Modelling Level” or m-ML to highlight its role as a supporting tool in macroscopic modelling. The effect of processes occurring in the remaining pores is modelled by another overlapping continuum, the macrostructure, designated as the “Macrostructural Modelling Level” or M-ML to detach it from topological meaning.

Whenever both continua have non-negligible porosity, they contribute together to the deformability of the system while accepting that flow concentrates in the M-ML. As the porosity associated with the M-ML becomes negligible, the proposed formulation assumes a residual macrostructural porosity bearing the presumably reduced hydraulic flow in the system. Therefore, neither the M-ML vanishes nor the hydraulic functionality of m-ML is activated. However, the deformability is then governed by the m-ML and the mechanical functionality of the M-ML is deactivated through a simple transition function. In addition, a model for the deformability of the system in such conditions is introduced assuming m-ML mechanical functionality only. This model is based on the volumetric bulk stiffness of the microstructural void ratio em, computed from the state surface relating em with the thermodynamic swelling pressure π.

The progressive trend of the system towards a deformational behaviour defined by the em–π relationship being the key hypothesis of the model, vertical oedometric loading tests were conducted aiming to confirm this phenomenon. The obtained results verify the hypothesis, backing the conceptual and qualitative consistency of the formulation.

The capability of the proposed approach to quantitatively reproduce the bentonite behaviour has been also evaluated using a displacement-based finite-element model. The implementation of the proposed conceptual model has been described for numerical models based on double porosity approaches, highlighting the reduced programming effort involved. The resulting numerical model was used to simulate the experiments with satisfactory results even with material parameters obtained from previous contributions, independent from the simulated tests in this work. Similarly, reported parameters from previous works were used to simulate a swelling pressure test by Massat et al. (2016). Although a challenging simulation due to the amount of experimental data on the evolution of the macroporosity distribution in the sample, acceptable fit was again observed.

This work has dealt with isothermal problems with reduced salinity and constant gas pressure. This study should be complemented with analyses of the effects of changes in temperature, salinity and gas pressure. Despite this, the obtained results highlight the simulation capability of the formulation. For this reason, and considering that (i) the application does not require any material parameters other than those of double porosity models, and (ii) the simplicity of the numerical implementation, it can be drawn that the presented approach is of interest to simulate the behaviour of compacted bentonites when the interaggregate porosity becomes minimal.