Introduction

In the 1950s and 1960s, the USGS investigated the role of seawater in the flow pattern of the Biscayne aquifer near Miami, Florida (Fig. 1), by measuring heads and chemistry in piezometer nests. Most of the essential data were collected, and their interpretations were published by Cooper et al. (1964). These authors also had published individual papers previously dealing with their part of these investigations as Cooper (1959), Glover (1959), Henry (1959, 1960a, b, 1962, 1964) and Kohout (1960a, b). All the above publications had a lasting impact on the way seawater intrusion was considered worldwide thereafter. The concept of wedge-shaped intrusion of saltwater under the freshwater of a coastal aquifer has been carried through much of the literature as well as the assumption of the occurrence of convection cells within the saltwater wedge, and the associated occurrence of dispersion as stated by Cooper et al. (1964).

Fig. 1
figure 1

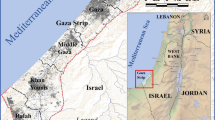
Location of Cutler site study area at Biscayne Bay and aquifer near Miami, Florida (red star). Map of North America modified after Wikipedia (creator: Bosonic dressing, 2009). For more detail, see Fig. 13. DEM by WDA Consultants Inc., 2016. Data derived from NASA’s Shuttle Radar Topography Mission (SRTM) dataset, extracted by the program GlobalMapper into a 764-m grid

Full size image

A selection of text books and handbooks spreading this concept includes Bear (2007a, Fig. 9–37, 2007b, Fig. 12.4), De Wiest (1965, Figs. 7–10, 7–11), Domenico (1972, Fig. 4.22), Fetter (1994, Fig. 9.34), Freeze and Cherry (1979, p. 378), Pinder and Celia (2006, Fig. 1.27), Schwartz and Zhang (2004, Fig. 8.34), Todd and Mays (2005, Fig. 14.4.1), and Walton (1970, Figs. 3.27, 3.28). All these books refer to the field work and the related data interpretation summarized by Cooper et al. (1964). Thus, the concepts contained in Cooper et al. (1964) have been widely adopted as a base for dealing with seawater intrusion and flow with contrasting density in coastal aquifers.

The postulated coastal saltwater wedge as the mechanism of saltwater intrusion in coastal aquifers by density-driven flow was also adopted into scientific literature and numerical modeling, as, for example, by Pinder and Cooper (1970, Figs. 3, 4 and 5), Lee and Cheng (1974, Figs. 3, 4 and 5), Segol and Pinder (1976), and Bear and Bachmat (1990, Fig. 8.41). Further examples for equal isochlor line calculation of salt wedges include the program SUTRA (Voss and Provost 2010, p. 169), as well as such journal articles as Lu et al. (2015, Fig. 1).

Langevin (2001) and Guo and Langevin (2002) explicitly developed the variable-density flow program system SEAWAT (a combined version of MODFLOW and MT3D) to deal with the simulation of complex variable-density groundwater flow pattern at Biscayne Bay. Langevin (2001) and Guo and Langevin (2002) verified the code SEAWAT ‘by running four different problems and comparing the results to those from other variable-density codes.’ These benchmark problems were (1) the Box problems (described in: Voss and Souza 1987), (2) the Henry problem (described in: Voss and Souza 1987), (3) the Elder Problem (described in Voss and Souza 1987) and (4) HYROCOIN (Hydrologic Code Intercomparison project) Problem #5 (described in: Konikow et al. 1997). The verification process did not include the Salt Lake problem (described in Simmons et al. 1999). Figure 2 depicts the concepts used for numerical modeling of coastal ground and seawater flow based on the interpretation of the Cutler site.

Fig. 2
figure 2

Conceptual hydrologic model used to develop numerical models of variable-density groundwater flow at Biscayne Bay showing postulated seawater wedge, zone of dispersion and convection cell (from Langevin 2001, Fig. 15). Note Figures originating from USGS publications have not been modified to maintain their original composition. These papers can be downloaded for free from USGS websites. Their URLs are listed in the list of references

Full size image

The concept of saltwater wedges and density-driven groundwater flow in coastal aquifers has since been applied to the coastal interaction of freshwater and seawater (Feseker 2007; Langevin and Zygnerski 2013; Merritt 1996; Shoemaker 2004; Werner and Simmons 2009; Werner et al. 2012.), water supply from coastal aquifers in Florida and elsewhere (Anderson et al. 1988; Rao et al. 2004; Spechler 1994), as well in the prediction of the effects of sea level rise in these aquifers (Masterson 2004; Masterson and Garabedian 2007; Rozell and Wong 2010).

As the saltwater wedge mechanism with its dispersion zone contradicts coastal flow patterns derived from numerical models which are built on gravitationally driven force potentials (Hubbert 1940, 1953; Tóth 1963; Freeze and Witherspoon 1967), the historical literature was revisited. The objective of this paper is to report the results of this review after first outlining the physical differences between ‘density-driven flow’ and gravitationally driven ‘groundwater flow systems.’ During this review, five independent methods will be used to prove that the saltwater wedge in the Biscayne aquifer has not been created by seawater intrusion, as assumed by Cooper et al. (1964), but by the discharge of regional groundwater flow systems, delivering saline groundwater from depth

  • the physics of ‘density-driven flow’ versus ‘groundwater flow systems,’

  • the occurrence of artesian (flowing) deep wells throughout South Florida,

  • the penetration depth of fresh groundwater to 600 m and more indicated by chemical data,

  • the occurrence of the freshwater/saltwater boundary in oil well P115 at approximately 1800 ft (600 m) about 10 miles (15 km) west of Biscayne Bay (Williams and Kuniansky (2016, plate 19),

  • the equal head lines of the equivalent freshwater heads as presented by Cooper et al. (1964) (Fig. 16 and 17).

Physics of density-driven flow and gravitational groundwater flow systems

Modern literature creates the impression that there is a fundamental difference in the physics of density-driven flow and that of groundwater flow systems. It is clear, however, that both ‘modes’ of flow are driven by gravitational forces. Thus, the question arises where the difference between the two modes lies. Unexpectedly the solution is relative simple: the difference lies in the boundary conditions; density-driven flow occurs under hydrostatic boundary conditions (Fig. 3, left side), while groundwater flow systems occur on land and under coastal areas under hydrodynamic conditions (Fig. 3, right side).

Fig. 3
figure 3

‘Density-driven flow’ under hydrostatic conditions versus gravitationally driven ‘groundwater flow systems’ under hydrodynamic conditions. From Weyer (2017b, after Weyer 1978)

Full size image

Under hydrostatic conditions, no flow occurs within equal-density fluids. The vectors for the resultant calculation are of the same magnitude with opposite vertical directions. Introducing an additional fluid of higher or lower density than the host fluid creates an upward or downward movement of the introduced fluid in dependence of its density as determined by simple resultant calculations (Fig. 4, left side). The created force is habitually called a ‘buoyancy force’ and is applied in strictly vertical directions: upwards or downwards. That is done not only under hydrostatic conditions but, erroneously, also under hydrodynamic conditions. Hydrostatic conditions (Fig. 4, left side) are a special case of hydrodynamic conditions (Fig. 4, right side).

Fig. 4
figure 4

Force vector calculation for density-driven flow under hydrostatic conditions versus gravitationally driven ‘groundwater flow systems’ under hydrodynamic conditions. After Weyer (2010, 2017b)

Full size image

Under hydrodynamic conditions, the pressure potential vector [– (grad p)/ρ] can occur in any direction in space (including vertically upwards and downwards), but then its magnitude is different from that of the gravitational vector g. Figure 4 (right side) visualizes schematically that under hydrodynamic conditions the resultant calculation for variable-density flow returns differing flow directions for the fluids of contrasting density. The vectors of the force fields are shown here in the force potential notation (Hubbert 1940). Hubbert (1953, p. 1982, Fig. 16 and accompanying text) shows that the density effects (‘buoyancy forces’) are added in the direction of the pressure potential gradient of the host fluid (freshwater) even in areas without freshwater (Hubbert 1953, p. 1960). Hence, the habitual addition of the assumed vertical ‘buoyancy forces’ to head forces is arbitrary and contradicts the laws of physics.

Here a paradigm shift occurs which contradicts the principles of ‘density-driven flow’ in any system with hydrodynamic boundary conditions in two respects (1) mixing of hydrodynamic with hydrostatic conditions and (2) application of velocity potential (energy/unit volume; assumption: incompressible fluid) instead of force potentials (energy/unit mass; compressible fluids).

This section outlined the physics involved in the problem addressed by this paper. In the following, the attention is first directed toward the general geology and lithology of Florida and subsequently to the field work undertaken by Cooper at al. (1964) and the interpretation of the field data obtained.

General tertiary and uppermost cretaceous geology and lithology of Florida

From a hydrodynamic point of view, the geology and lithology of Florida are dominated by sand layers at the surface and carbonates and minor sandstone layers at greater depth. These types of fractured and often karstic rocks facilitate the formation of far-reaching regional groundwater flow systems even at the moderate elevation differences of less than 100 m between recharge and discharge areas.

The Tertiary (Paleocene) carbonates are part of the Upper Floridan and Lower Floridan Aquifer systems overlain, separated, and underlain by confining layers (Fig. 5). The Cedar Keys Formation forms the lower confining unit and is located above the uppermost Cretaceous layer, the Lawson Formation of carbonate lithology.

Fig. 5
figure 5

Hydrogeologic framework of the Floridian aquifer system, depth of freshwater regional groundwater flow system as indicated by the boundary between flowing freshwater and static saltwater (after Bush and Johnson 1986, Fig. 9). The figure text here has been redone, and the interface between the freshwater and saltwater highlighted in red to improve clarity

Full size image

Interpretation of chemical field data for flow of freshwater and saltwater in the Biscayne aquifer

The distribution of the isochlor lines in Fig. 6 creates the optical impression that seawater is flowing at the bottom of the Biscayne aquifer away from Biscayne Bay. Such is the explicit explanation which was given by the USGS (Miller 1990, Fig. 39) as shown in Fig. 7. The same interpretation has been adopted by all text books quoted in the introduction above.

Fig. 6
figure 6

Section through the Cutler area near Miami, showing chemical sampling points and isochlor lines in ppm within the Biscayne aquifer for September 8, 1958 (from Cooper et al. 1964, Fig. 5)

Full size image
Fig. 7
figure 7

Widely accepted interpretation of chemical data for freshwater and seawater flow in the Cutler section near Miami within the Biscayne aquifer (from Miller 1990, Fig. 39)

Full size image

Schwartz and Zhang (2004) incorporated Miller’s (1990) Fig. 39 as their Fig. 8.34. This data interpretation fits well into the widely spread opinion that chemical data and isotope data are adequate to determine flow direction within groundwater flow systems. This paper will show that interpretations based solely on chemistry may be prone to unfounded conclusions. Chemical and isotope investigations should always be supported by head measurements of groundwater flow systems taking density variations into account.

Admittedly, the equal isochlor lines in Fig. 6 lent themselves to the quick interpretation of hydrodynamical flow pattern as shown in Fig. 7.

Interpretation of head data for flow of freshwater and saltwater in the Biscayne aquifer

While Cooper (1959), Glover (1959), Henry (1959, 1960a, b, 1962) and Kohout (1960a, b) only show a selection of field data, Cooper et al. (1964) reported hydraulic field data as equivalent freshwater heads. They indicate the general flow directions of freshwater and saltwater in the Biscayne aquifer, close to and under parts of Biscayne Bay. Kohout (1964, p. C28) interprets the associated flow directions in his Figs. 15–17 as follows:

The equipotential lines in the upper, freshwater part of the aquifer indicate the potential of freshwater in a freshwater environment and hence indicate comparative potentials. As flow lines must be nearly perpendicular to these equipotential lines, a seaward movement of freshwater is indicated.

In the lower and seaward part of the aquifer, the equipotential lines indicate the potential of freshwater in a region occupied by saltwater. The freshwater equipotential surfaces in a region occupied by saltwater will be horizontal if the saltwater is static. As the equipotential lines in the saltwater regions of Figs. 15 to 17 are not horizontal but slope inland in Fig. 15, seaward in Fig. 16, and inland in Fig. 17, the saltwater is not static but must be in motion in the direction of the slope. [emphasis added]

Kohout’s (1964) Fig. 16 has been reproduced here as Fig. 8. As Kohout (1964, pages C12–C35 in Cooper et al. 1964) himself clearly stated above that ‘flow lines must be nearly perpendicular to these equipotential lines,’ it is difficult to grasp why he then concludes above that ‘the salt water must be in motion in the direction of the slope’ of the equipotential lines which to him implied lateral flow of seawater into the Biscayne aquifer.

Fig. 8
figure 8

Cross section through the Cutler area, near Miami, Fla., showing lines of equal freshwater heads at 0750 (bay low tide) September 18, 1958 (From Cooper et al. 1964, Fig. 16). Blue flow arrows added showing upward flow of deep seated groundwater flow systems carrying salt from the Paleocene Cedar Keys formation

Full size image

It is even more perplexing as Kohout (1964) stated on page C23:

Where the density varies from point to point, measurements of head do not indicate the direction of movement directly. For this reason the observed saltwater heads in the wells have been converted to freshwater heads by computation.

The point of computing equivalent freshwater heads is that they are supposedly suited to determine the flow directions of freshwater and saltwater alike, or at least the general trend of the flow pattern. Accordingly, the approximate flow directions within the saltwater portion of Figs. 8 and 9 were inserted by hand.

Fig. 9
figure 9

Cross section through the Cutler area, near Miami, Fla., showing lines of equal freshwater heads for a low-head condition average for September 18, 1958 (from Cooper et al. 1964, Fig. 17). Blue flow arrows added showing upward flow of deep seated groundwater flow systems carrying salt from the Paleocene Cedar Keys formation

Full size image

The inserted flow lines are perpendicular to lines of equal equivalent freshwater heads as they should be according to above statements by Kohout himself. It is therefore clear that this is not a saltwater wedge created by flow of seawater from Biscayne Bay. Instead the saltwater has been transmitted by discharging saline regional groundwater flow systems from the Cedar Keys Formation. Stringfield (1966, p. 36) reported for the Cedar Keys Formation chloride concentration of up to 23,000 and of 53,000 ppm in the underlying Lawson Formation.

Figure 10 documents how Kohout (1964, in Cooper et al. 1964) adopts the interpretation of the encountered flow pattern, clearly supporting the postulates of density-driven flow, diffusion and dispersion as well as convection flow at this location. This interpretation then promoted the acceptance of the occurrence of seawater wedges in coastal aquifers worldwide.

Fig. 10
figure 10

Cross section through the Cutler area, near Miami, Fla., showing the postulated pattern of flow of fresh and saltwater for a low-head condition, September 18, 1958 (from Cooper et al. 1964, Fig. 19)

Full size image

Henry’s (1964) simulation of seawater flow from Biscayne Bay into the Biscayne aquifer (Fig. 11) reflected neither the head measurements nor the interpretation based on equal isochlor lines (compare Figs. 6, and 7). In the field, the conditions were unconfined and not confined as assumed in Henry’s simulation. One could suspect that Henry (1964) needed to assume confined conditions in order to accommodate an analytical mathematical solution. From then on this limitation has determined the procedures used worldwide to simulate saltwater intrusion.

Fig. 11
figure 11

Flow and salt concentration patterns in an idealized mathematical model. Model calculated by Henry (1964) in Cooper et al. (1964), Fig. 34, known as the ‘Henry problem’ which new variable-density flow computer programs must meet to be considered functional

Full size image

Figure 11 taken from Henry (1964, Fig. 34), however, forms the blueprint for solving the Henry problem. Voss and Provost (2010, p. 169) state as ‘Physical Setup’ for ‘Density dependant flow and solute transport (Henry 1964 ) solution for seawater intrusion’ as follows:

This problem involves seawater intrusion into a confined aquifer studied in cross section under steady conditions. Freshwater recharge inland flows over saltwater in the section and discharges at a vertical sea boundary.

The intrusion problem is nonlinear and may be solved by approaching the steady state gradually with a series of time steps. Initially there is no saltwater in the aquifer, and at time zero, saltwater begins to intrude the freshwater system by moving under the freshwater from the sea boundary. The intrusion is caused by the greater density of the saltwater.

Dimensions of the problem are selected to make for simple comparison with the steady-state dimensionless solution of Henry (1964), and with a number of other published simulation models. A total simulation time of t = 100.0 [min], is selected, which is sufficient time for the problem to essentially reach steady state at the scale simulated.

The simulated flow patterns do not do justice to the actual flow and head patterns measured by Kohout (1964) at the site for which the Henry problem had been developed. The pattern measured can only be explained by the pattern of gravity-driven regional groundwater flow systems prevailing in central and south Florida. H.H. Cooper Jr, the main author in Cooper and al. (1964) and the coauthor of the paper by Pinder and Cooper (1970), was actively involved in developing the salt wedge concept reported by Kohout (1964).

Manifestation of deep regional flow systems in Florida

It has been shown above that the equal isochlor lines at the Cutler area near Miami have been caused by upward discharge of fresh and saline deep groundwater as well as lateral discharge of shallower fresh groundwater. While it is not difficult to locate nearby recharge areas for more local groundwater flow systems, as defined by Tóth (1963), the question arises where the deep regional part of the groundwater flow systems recharges. This paper owes the answer to the work by Healy (1962a, b) and the summary description by Stringfield (1966). The recharge areas for the deep groundwater flow systems in South Florida are the Central Highlands from which the regional groundwater flow systems migrate to the eastern and western Coastal Low Lands as well as to South Florida (see Fig. 12). Due to the energy needed for upward discharge against gravitational forces, discharge areas are always characterized by artesian (flowing) wells. Stringfield (1966, Fig. 29) indicated the artesian heads in the Floridian aquifer to be at about 6 mamsl (20 ft amsl) elevation at the coast of the Biscayne Bay and about 16 mamsl (50 ft amsl) at Lake Okeechobee.

Fig. 12
figure 12

Areas of artesian flow from regional groundwater flow systems (dark). The recharge areas for deep groundwater flow appear white (from Stringfield 1966, Fig. 28). Red arrow marks the position of the Cutler site, Biscayne Bay, near Miami, Fla

Full size image

The penetration depth of the flow system is indicated in Fig. 5 along a cross section in Central Florida to be about 800 m (~ 2400 ft). Recharge areas in the Central Highlands reach elevations exceeding 70 mamsl. These elevations suffice to maintain, within the Floridian aquifer system, regional flow systems to the coasts at the Atlantic, south Florida and the Gulf of Mexico. It is not quite clear which definition of freshwater had been used by Bush and Johnson (1986). In any case, however, the boundary given between fresh and saltwater reliably indicates the general penetration depth of groundwater flow under the recharge area. About 10 miles west of Biscayne Bay, Williams and Kuniansky (2016, plate 19) report in oil well P115 the freshwater—saltwater boundary at an approximate depth of 1800 ft (~ 600 m) with an TDS concentration of approximately 10,000 mg/l. This indicates that the regional groundwater discharge of saline water at Biscayne Bay migrated upwards from a depth of about 600 m or more. This explains the salt concentrations reported as equal isochlor lines in Fig. 6. The isochlor lines have not been created by seawater flow from Biscayne Bay and the action of a zone of dispersion as postulated by Kohout (1964) in Cooper et al. (1964). This dispersion zone and the postulated coastal convection flow zone did and do not exist.

The salt wedge interpretation forwarded by Kohout (1964, in Cooper et al. 1964) constitutes a severe misunderstanding and misinterpretation of field data, and in view of the importance for coastal water supply, the new understanding needs to be included in numerical modeling and proper practical water supply management world-wide.

An outline of the deep groundwater flow system leading from the Central Florida Uplands to Biscayne Bay is shown schematically in Fig. 13 (topographic trace of cross section) and in Fig. 14 (cross section schematically showing regional and local groundwater flow systems).

Fig. 13
figure 13

Digital elevation model (DEM) of central and south Florida showing trace of cross section displayed in Fig. 14 and position of the Cutler site at the Biscayne Bay. DEM by WDA Consultants Inc., 2016. Data derived from NASA’s Shuttle Radar Topography Mission (SRTM) dataset, extracted by the program GlobalMapper into a 764-m grid

Full size image
Fig. 14
figure 14

Cross section of central and south Florida (location in Fig. 13). Very schematic outline of flow lines from the central Florida uplands to Biscayne Bay. Vertical exaggeration 400:1 (left) and 100:1 (below)

Full size image

Conclusions

In an attempt to explain the pattern of equal isochlor lines at a test site for saltwater intrusion at Biscayne Bay near Miami (Cooper et al. 1964), groundwater flow pattern was derived from chemical data and an analytical model calculation and taken as proof for the invasion of seawater into the Biscayne aquifer. Contemporaneously measured head data were in stark contrast to this conclusion. The application of this procedure and its conclusions may be understandable as in the 1950s and early 1960s the role of aquitards was not yet fully recognized as efficient transmitters of groundwater flow and the classical papers on groundwater flow systems had not been published yet.

That may be one reason why the influence of the publications by Cooper (1959), Kohout (1960a, b) and Henry (1959, 1960a, b, 1962) and Cooper et al. (1964) dominated the conceptual understanding of seawater intrusion and its numerical analysis under conceptually assumed boundary conditions. These concepts became an important part of textbooks, scientific literature on variable-density flow, density-driven flow, free convection and the management of coastal water supplies.

Revisiting the field data of Cooper et al. (1964), in view of groundwater flow systems theory (Tóth 1963; Freeze and Witherspoon 1967), paves the way for a paradigm shift in such that the chemical and hydrodynamic head data have been caused by regional discharge of saline groundwater from a depth of 600 m or more and not by density-driven convection flow of seawater from Biscayne Bay. Furthermore, as seawater does not enter the aquifer under non-pumping conditions, neither at low nor at high tide, the postulated zone of dispersion and a saltwater wedge do not exist at the coast of Biscayne Bay and, in all likelihood, also not at the rest of the Floridian coast line and at other coasts with hilly topography worldwide.

In summary, the case of the discharge of deep saline groundwater in the Biscayne Bay area has been proven by five independent methods

  • the physics of ‘density-driven flow’ versus ‘groundwater flow systems,’

  • the occurrence of artesian (flowing) deep wells throughout South Florida (Fig. 11),

  • the penetration depth of fresh groundwater to 600 m and more indicated by chemical data (Fig. 12),

  • the occurrence of the freshwater/saltwater boundary in oil well P115 at approximately 1800 ft (600 m) about 10 miles (15 km) west of Biscayne Bay (Williams and Kuniansky (2016, plate 19),

  • the equal head lines of the equivalent freshwater heads (Figs. 8, 9) as presented by Cooper et al. 1964 (Fig. 16, 17).

Of course, seawater may penetrate coastal aquifers once significant pumping has commenced and, due to a change of the pattern of groundwater flow systems, it may fill voids created by pumping. For optimal management of water supply, the portion of deep saline groundwater to seawater should be determined by application of numerical simulators capable of dealing with density-dependant buoyancy modifications along the direction of the pressure potential forces as in the right-hand side of Fig. 4.

An outlook on the future development of the understanding and application of variable density flow in research and practice as well as the related need for new computer codes is given by Weyer (2017a).