Skip to main content
SpringerLink
Log in

Changes in fluid flux and hydraulic head in a geothermal confined aquifer

  • Original Article
  • Published:
Environmental Earth Sciences Aims and scope Submit manuscript

Abstract

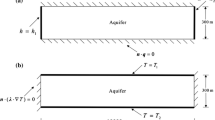
Understanding the changes in fluid flux and hydraulic head in a confined aquifer where heat flow from below exists is important in the development of a geothermal field of basin-type. A 3D mathematical model describing thermal groundwater flow and heat transport is established. The partial differential governing equations are solved with the standard Galerkin finite element method and the streamline upwind Petrov–Galerkin method. Two cases of temperature differences between the bottom and upper boundaries are considered and one case of hydraulic gradient difference between the left and right boundaries are also examined. The numerical results show that when the temperature of the aquifer is under normal temperature and the temperatures of the top boundary are 45, 50 and 55 °C with the temperature of the bottom boundary of 60 °C, the values of fluid flux through the vertical flow section are 1000, 2134, 2214 and 2295 m3/d in Case 2, which are mainly affected by the dynamic viscosity \(u\). When the temperature difference between the top and bottom boundaries increases, the hydraulic gradient in x direction slightly increases with the increasing temperature difference. When the temperature differences are 15, 10, 5 and 0 °C, respectively, the hydraulic gradients are 0.01005, 0.01003, 0.01002 and 0.01 in Cases 1 and 2, and almost keep the same value of 0.01 under normal temperature. The hydraulic head in z direction obeys a nonlinear change and can be described with a 2nd order polynomial function.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  • Ataie-Ashtiani B, Simmons CT, Werner AD (2014) Influence of boundary condition types on unstable density-dependent flow. Groundwater 52:378–387

    Article  Google Scholar 

  • Bear J (1972) Dynamics of fluids in porous media. American Elsevier, NewYork

  • Bear J (1979) Hydraulics of groundwater. McGraw-Hill, London

    Google Scholar 

  • Brebbia CA, Zamani NG (1987) Boundary element techniques: applications in fluid flow and computational aspects. Computational Mechanics Publications, Southampton

    Google Scholar 

  • Brooks AN, Hughes TJ (1982) Streamline upwind/Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equations. Comput Methods Appl Mech Eng 32:199–259

    Article  Google Scholar 

  • Chen M, Wang J, Deng X (1994) Geothermal resources in China. Science Press, Beijing (In Chinese)

    Google Scholar 

  • COMSOL (2013) COMSOL multiphysics modeling guide (version 4.4). COMSOL AB, Stockholm

  • Diersch H-JG (2002) About the difference between the convective form and divergence form of transport equation. FEFLOW-White papers, vol I, WASY Ltd, Berlin

  • Diersch H-JG (2005b) FEFLOW Reference Manual WASY GmbH Institute for Water Resources Planning and Systems Research Ltd, Berlin

  • Diersch H-JG (2005a) FEFLOW-White papers, vol I. WASY GmbH Institute for Water Resources Planning and Systems Research Ltd, Berlin

    Google Scholar 

  • Diersch H-JG, Kolditz O (2002) Variable-density flow and transport in porous media: approaches and challenges. Adv Water Resour 25:899–944

    Article  Google Scholar 

  • Elder J (1967) Transient convection in a porous medium. J Fluid Mech 27:609–623

    Article  Google Scholar 

  • Harbaugh AW (2005) MODFLOW-2005, the US Geological Survey modular ground-water model: The ground-water flow process US Department of the Interior, US Geological Survey

  • Heggen RJ (1983) Thermal dependent physical properties of water. J Hydraul Eng 109:298–302

    Article  Google Scholar 

  • Huang K, Mohanty B, Van Genuchten MT (1996) A new convergence criterion for the modified Picard iteration method to solve the variably saturated flow equation. J Hydrol 178:69–91

    Article  Google Scholar 

  • Huyakorn PS, Andersen PF, Mercer JW, White HO (1987) Saltwater intrusion in aquifers: development and testing of a three-dimensional finite element model. Water Resour Res 23:293–312

    Article  Google Scholar 

  • Kipp KL (1987) HST3D: a computer code for simulation of heat and solute transport in three-dimensional ground-water flow systems U.S. Geological Survey, Water-Resources Investigations Report, 86-4095

  • Li Q, Wang N, Yi D (2005) Numerical analysis. Tsinghua University Press, Beijing (In Chinese)

    Google Scholar 

  • Lin W, Liu Z, Wang W, Wang G (2013) The assessment of geothermal resources potential of China. Geol China 40:312–321

    Google Scholar 

  • Lusczynski NJ (1961) Head and flow of ground water of variable density. J Geophys Res 66:4247–4256

    Article  Google Scholar 

  • Nadukandi P, Oñate E, Garcia J (2010) A high-resolution Petrov-Galerkin method for the 1D convection-diffusion-reaction problem. Comput Methods Appl Mech Eng 199:525–546

    Article  Google Scholar 

  • Ophori DU (1998) The significance of viscosity in density-dependent flow of groundwater. J Hydrol 204:261–270

    Article  Google Scholar 

  • Post V, Kooi H, Simmons C (2007) Using hydraulic head measurements in variable-density ground water flow analyses. Ground Water 45:664–671

    Article  Google Scholar 

  • Pruess K, Oldenburg C, Moridis G (1999) TOUGH2 user’s guide version 2 earth sciences division. Lawrence Berkeley National Laboratory University of California, Berkeley, California

    Book  Google Scholar 

  • Putti M, Paniconi C (1995) Picard and Newton linearization for the coupled model for saltwater intrusion in aquifers. Adv Water Resour 18:159–170

    Article  Google Scholar 

  • Simmons CT, Fenstemaker TR, Sharp JM Jr (2001) Variable-density groundwater flow and solute transport in heterogeneous porous media: approaches, resolutions and future challenges. J Contam Hydrol 52:245–275

    Article  Google Scholar 

  • Simmons C, Bauer-Gottwein P, Graf T, Kinzelbach W, Kooi H, Li L, Post V, Prommer H, Therrien R, Voss C (2010) Variable density groundwater flow: from modelling to applications. Cambridge University Press, Cambridge

    Google Scholar 

  • Simpson M, Clement T (2003) Theoretical analysis of the worthiness of Henry and Elder problems as benchmarks of density-dependent groundwater flow models. Adv Water Resour 26:17–31

    Article  Google Scholar 

  • Smith L, Chapman DS (1983) On the thermal effects of groundwater flow: 1. Regional scale systems. J Geophys Res Solid Earth (1978–2012) 88:593–608

    Article  Google Scholar 

  • Voss CI (1984) A finite-element simulation model for saturated-unsaturated, fluid-density-dependent ground-water flow with energy transport or chemically-reactive single-species solute transport. US Geological Survey

  • Voss CI, Souza WR (1987) Variable density flow and solute transport simulation of regional aquifers containing a narrow freshwater-saltwater transition zone. Water Resour Res 23:1851–1866

    Article  Google Scholar 

  • Wang H (2008) Dynamics of fluid flow and contaminant transport in porous media. Higher Education Press, Beijing, pp 481–484 (In Chinese)

    Google Scholar 

  • Wang X (2011) Groundwater movement equation. Geological Publishing House, Beijing (In Chinese)

    Google Scholar 

  • Wang J, Xiong L, Pang Z (1993) Low-medium temperature geothermal system of convective type. Science Press, Beijing (In Chinese)

    Google Scholar 

  • Woods JA, Carey GF (2007) Upwelling and downwelling behavior in the Elder-Voss-Souza benchmark. Water Resou Res 43

  • Xue Y, Xie C (2007) Numerical simulation of groundwater. Science Press, Beijing (In Chinese)

    Google Scholar 

  • Zhou X, Chen M, Li C (2001a) 3-Dimensional numerical modeling of geothermal water flow in deep-seated aquifers. Geological Publishing House, Beijing (In Chinese)

    Google Scholar 

  • Zhou X, Chen M, Zhao W, Li M (2001b) Modeling of a Deep-Seated Geothermal System Near Tianjin, China. Ground Water 39:443–448

    Article  Google Scholar 

  • Zienkiewicz O, Wu J (1992) A general explicit or semi-explicit algorithm for compressible and incompressible flows. Int J Numer Meth Eng 35:457–479

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by the Natural Science Foundation of Beijing (8152026), the Fundamental Research Funds for the Central Universities of China (2652013085, 2652014089, 2652015244, 2652015245, 2562015426) and the project of China Geological Survey (1212011120064).

Author information

Authors and Affiliations

  1. School of Water Resources and Environment, China University of Geosciences (Beijing), Xueyuan Road 29, Beijing, 100083, People’s Republic of China

    Jingbo Zhao, Xun Zhou, Yuan Yu, Chuanxia Ruan, Xiaocui Wang, Jingwei Li, Qingxiao Zhang & Xiaowei Shen

  2. Beijing Research Institute of Uranium Geology (BRIUG), 10, Xiao-Guan-Dong-Li, P.O. Box 9818, Beijing, 100029, People’s Republic of China

    Jingbo Zhao

  3. Key Laboratory of Groundwater Circulation and Evolution, Ministry of Education, China University of Geosciences (Beijing), Xueyuan Road 29, Beijing, 100083, People’s Republic of China

    Xun Zhou

  4. Beijing Geology Prospecting and Developing Bureau, No.123 West 4th Ring North Road, Beijing, 100195, People’s Republic of China

    Yuan Yu

  5. Tianjin Geothermal Exploration and Development-Designing Institute, Weiguo Road 189, Tianjin, 300250, People’s Republic of China

    Chuanxia Ruan

Authors
  1. Jingbo Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xun Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yuan Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Chuanxia Ruan
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Xiaocui Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Jingwei Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Qingxiao Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Xiaowei Shen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xun Zhou.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhao, J., Zhou, X., Yu, Y. et al. Changes in fluid flux and hydraulic head in a geothermal confined aquifer. Environ Earth Sci 75, 397 (2016). https://doi.org/10.1007/s12665-016-5248-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12665-016-5248-7

Keywords

Search

Navigation