An inventory model with preservation technology investments and stock-varying demand under advanced payment scheme

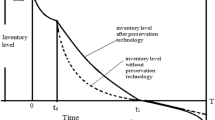
Abstract

In traditional EOQ models, retailers pay suppliers the purchase price of an order as soon as it arrives. But in today competitive market, however, suppliers may offer retailers the option to pay all or a portion of the product value in advance in return for specific incentives, such as an immediate price discount and other perks. In this article, an EOQ inventory model for retailers with deteriorating commodities employing preservation technologies and a partially advanced payment method has been established. The product’s demand is in stock dependent. We proved optimality both analytically and visually, and we offered one theorem to demonstrate optimality theoretically. Two numerical examples are offered to prove the validity of present inventory model. We used MATLAB to create 3D graphs to evaluate the numerical results of the suggested model. Finally, we conducted a sensitivity analysis by altering a single parameter while leaving the others unchanged.

Appendices

Appendix 1

Proof of theorem 1:

To prove the theorem we will first find all three second derivative of $Z\left( {t_{2} ,t_{3} } \right)$ with respect to $t_{2}$ and $t_{3}$ (see appendix 2).

We know that a function $f\left( {x,y} \right)$ is minimum if (i) $\frac{{\partial^{2} f}}{{\partial x^{2} }}\frac{{\partial^{2} f}}{{\partial y^{2} }} - \frac{{\partial^{2} f}}{\partial x\partial y} > 0$ (ii) $\frac{{\partial^{2} f}}{{\partial x^{2} }} > 0$ and $\frac{{\partial^{2} f}}{{\partial y^{2} }} > 0$.

Case 1:

$$ {\text{if}} \left[ {\frac{{\partial^{2} Z\left( {t_{2} ,t_{3} } \right)}}{{\partial t_{2}^{2} }}} \right]_{{at\, t_{2} = t_{2}^{*} }} > 0\;{\text{and }}\;\left[ {\frac{{\partial^{2} Z\left( {t_{2} ,t_{3} } \right)}}{{\partial t_{3}^{2} }}} \right]_{{at\, t_{3} = t_{3}^{*} }} > 0 $$

(21)

We take

$\begin{gathered} \left[ {\frac{{\partial^{2} Z\left( {t_{2} ,t_{3} } \right)}}{{\partial t_{2}^{2} }}} \right]_{{at\, t_{2} = t_{2}^{*} }} \cdot { }\left[ {\frac{{\partial^{2} Z\left( {t_{2} ,t_{3} } \right)}}{{\partial t_{3}^{2} }}} \right]_{{at\, t_{3} = t_{3}^{*} }} - \left[ {\frac{{\partial^{2} Z\left( {t_{2} ,t_{3} } \right)}}{{\partial t_{2} \partial t_{3} }}} \right]_{{at\, t_{2} = t_{2, }^{*} t_{3} = t_{3}^{*} }} \hfill \\ = \left[ {\frac{{\partial^{2} Z\left( {t_{2} ,t_{3} } \right)}}{{\partial t_{2}^{2} }}} \right]_{{at\, t_{2} = t_{2}^{*} }} .{ }\left[ {\frac{{\partial^{2} Z\left( {t_{2} ,t_{3} } \right)}}{{\partial t_{3}^{2} }}} \right]_{{at\, t_{3} = t_{3}^{*} }} > 0 \hfill \\ \end{gathered}$ (by Eq. (17))

(Since $\left[ {\frac{{\partial^{2} Z\left( {t_{2} ,t_{3} } \right)}}{{\partial t_{2} \partial t_{3} }}} \right] = 0$ at all points

Hence $Z\left( {t_{2} ,t_{3} } \right)$ attend minimum value at $t_{2}^{*}$ and $t_{3}^{*}$.

Case 2:

$$ {\text{if }}\left[ {\frac{{\partial^{2} Z\left( {t_{2} ,t_{3} } \right)}}{{\partial t_{2}^{2} }}} \right]_{{at\, t_{2} = t_{2}^{*} }} < 0\;{\text{and}}\;\left[ {\frac{{\partial^{2} Z\left( {t_{2} ,t_{3} } \right)}}{{\partial t_{3}^{2} }}} \right]_{{at\, t_{3} = t_{3}^{*} }} < 0 $$

(22)

We take

$\begin{gathered} \left[ {\frac{{\partial^{2} Z\left( {t_{2} ,t_{3} } \right)}}{{\partial t_{2}^{2} }}} \right]_{{at\, t_{2} = t_{2}^{*} }} \cdot { }\left[ {\frac{{\partial^{2} Z\left( {t_{2} ,t_{3} } \right)}}{{\partial t_{3}^{2} }}} \right]_{{at\, t_{3} = t_{3}^{*} }} - \left[ {\frac{{\partial^{2} Z\left( {t_{2} ,t_{3} } \right)}}{{\partial t_{2} \partial t_{3} }}} \right]_{{at\, t_{2} = t_{2, }^{*} t_{3} = t_{3}^{*} }} \hfill \\ = \left[ {\frac{{\partial^{2} Z\left( {t_{2} ,t_{3} } \right)}}{{\partial t_{2}^{2} }}} \right]_{{at\, t_{2} = t_{2}^{*} }} \cdot z\left[ {\frac{{\partial^{2} Z\left( {t_{2} ,t_{3} } \right)}}{{\partial t_{3}^{2} }}} \right]_{{at\, t_{3} = t_{3}^{*} }} > 0 \hfill \\ \end{gathered}$(by Eq. (18)

(Since $\left[ {\frac{{\partial^{2} Z\left( {t_{2} ,t_{3} } \right)}}{{\partial t_{2} \partial t_{3} }}} \right] = 0$ at all points (see appendix))

Hence $Z\left( {t_{2} ,t_{3} } \right)$ attend minimum value at $t_{2}^{*}$ and $t_{3}^{*}$.

Therefor $Z\left( {t_{2} ,t_{3} } \right)$ attends a minimum value at $t_{2}^{*}$ and $t_{3}^{*}$ if second derivative $\frac{{\partial^{2} Z\left( {t_{2} ,t_{3} } \right)}}{{\partial t_{2}^{2} }}$ and $\frac{{\partial^{2} Z\left( {t_{2} ,t_{3} } \right)}}{{\partial t_{3}^{2} }}$ are either positive or negative at $t_{2}^{*}$ and $t_{3}^{*}$. This completes the proof.

Appendix 2

Computing the partial derivatives of $Z({t}_{2},{t}_{3})$ with respect to ${t}_{2}and {t}_{3}$:

$$ \begin{aligned} \frac{{\partial Z\left( {t_{2} ,t_{3} } \right)}}{{\partial t_{2} }} = & - ac_{p} e^{{ - \left( {\alpha t_{1}^{\beta } - m\left( \xi \right)t_{1} } \right)}} \cdot e^{{\left( {\alpha t_{2}^{\beta } - m\left( \xi \right)t_{2} + bt_{2} } \right)}} \\ & \; + h_{1} \left[ { ae^{{ - \left( {\alpha t_{1}^{\beta } - m\left( \xi \right)t_{1} } \right)}} \cdot e^{{\left( {\alpha t_{2}^{\beta } - m\left( \xi \right)t_{2} + bt_{2} } \right)}} \left\{ {\frac{{t_{1} e^{{ - bt_{1} }} }}{b} + \frac{{(e^{{ - bt_{1} }} - 1)}}{{b^{2} }} + \frac{{at_{1}^{2} }}{2b} } \right\}} \right] \\ & \; + h_{2} \left[ { ae^{{ - \left( {\alpha t_{1}^{\beta } - m\left( \xi \right)t_{1} } \right)}} \cdot e^{{\left( {\alpha t_{2}^{\beta } - m\left( \xi \right)t_{2} + bt_{2} } \right)}} \left\{ { \frac{{(e^{{ - bt_{1} }} - 1)}}{b} + \frac{{at_{1} }}{b} } \right\}} \right] \\ & \; - ah_{1} \left[ {\mathop \smallint \limits_{{t_{1} }}^{{t_{2} }} te^{{ - \left( {\alpha t^{\beta } - m\left( \xi \right)t + bt} \right)}} \cdot \left( {e^{{\left( {\alpha t_{2}^{\beta } - m\left( \xi \right)t_{2} + bt_{2} } \right)}} } \right) + t_{2} e^{{ - \left( {\alpha t_{2}^{\beta } - m\left( \xi \right)t_{2} + bt_{2} } \right)}} \mathop \smallint \limits_{{t_{1} }}^{{t_{2} }} e^{{\left( {\alpha t^{\beta } - m\left( \xi \right)t + bt} \right)}} dt} \right] \\ & \; - ah_{2} \left[ {\mathop \smallint \limits_{{t_{1} }}^{{t_{2} }} e^{{ - \left( {\alpha t^{\beta } - m\left( \xi \right)t + bt} \right)}} \cdot \left( {e^{{\left( {\alpha t_{2}^{\beta } - m\left( \xi \right)t_{2} + bt_{2} } \right)}} } \right) + e^{{ - \left( {\alpha t_{2}^{\beta } - m\left( \xi \right)t_{2} + bt_{2} } \right)}} \mathop \smallint \limits_{{t_{1} }}^{{t_{2} }} e^{{\left( {\alpha t^{\beta } - m\left( \xi \right)t + bt} \right)}} dt} \right] \\ & \; - ae^{{ - \left( {\alpha t_{1}^{\beta } - m\left( \xi \right)t_{1} + bt_{1} } \right)}} \cdot e^{{\left( {\alpha t_{2}^{\beta } - m\left( \xi \right)t_{2} + bt_{2} } \right)}} + a^{2} \mathop \smallint \limits_{{t_{1} }}^{{t_{2} }} e^{{ - \left( {\alpha t^{\beta } - m\left( \xi \right)t + bt} \right)}} \cdot e^{{\left( {\alpha t_{2}^{\beta } - m\left( \xi \right)t_{2} + bt_{2} } \right)}} \\ & \; + e^{{ - \left( {\alpha t_{2}^{\beta } - m\left( \xi \right)t_{2} + bt_{2} } \right)}} \cdot \mathop \smallint \limits_{{t_{1} }}^{{t_{2} }} e^{{\left( {\alpha t^{\beta } - m\left( \xi \right)t + bt} \right)}} dt - \frac{{i_{c} \omega \sigma \left( {\eta + 1} \right)c_{p} }}{2\eta } \left[ { ae^{{ - \left( {\alpha t_{1}^{\beta } - m\left( \xi \right)t_{1} } \right)}} \cdot e^{{\left( {\alpha t_{2}^{\beta } - m\left( \xi \right)t_{2} + bt_{2} } \right)}} } \right] \\ \end{aligned} $$

(23)

$$ \frac{{\partial Z\left( {t_{2} ,t_{3} } \right)}}{{\partial t_{3} }} = \frac{{C_{p} a}}{{1 + \delta t_{3} }} + \frac{{C_{b} a}}{\delta } \left( { 1 - \frac{1}{{1 + \delta t_{3} }} } \right) + \frac{{i_{c} \omega \sigma \left( {\eta + 1} \right)}}{2\eta } \cdot \frac{{C_{p} a}}{{1 + \delta t_{3} }} + C_{1} a\left( {1 - \frac{1}{{1 + \delta t_{3} }} } \right) $$

(24)

$$ \begin{aligned} \frac{{\partial ^{2} Z\left( {t_{2} ,t_{3} } \right)}}{{\partial t_{2}^{2} }} = & - a\left( {\alpha \beta t_{2}^{{\beta - 1~}} - m\left( \xi \right) + b} \right)e^{{ - \left( {\alpha t_{1}^{\beta } - m\left( \xi \right)t_{1} } \right)}} \cdot e^{{\left( {\alpha t_{2} - m\left( \xi \right)t_{2} + bt_{2} } \right)}} \\ & \; + h_{1} \left[ {a\left( {\alpha \beta t_{2}^{{\beta - 1~}} - m\left( \xi \right) + b} \right)e^{{ - \left( {\alpha t_{1}^{\beta } - m\left( \xi \right)t_{1} } \right)}} \cdot e^{{\left( {\alpha t_{2} - m\left( \xi \right)t_{2} + bt_{2} } \right)}} \left\{ {~\frac{{t_{1} e^{{ - bt_{1} }} }}{b} + \frac{{\left( {e^{{ - bt_{1} }} - 1} \right)}}{{b^{2} }} + \frac{{at_{1}^{2} }}{{2b}}~} \right\}} \right] \\ & \; + h_{2} \left[ {~a\left( {\alpha \beta t_{2}^{{\beta - 1~}} - m\left( \xi \right) + b} \right)e^{{ - \left( {\alpha t_{1}^{\beta } - m\left( \xi \right)t_{1} } \right)}} \cdot e^{{\left( {\alpha t_{2} - m\left( \xi \right)t_{2} + bt_{2} } \right)}} \left\{ {~\frac{{\left( {e^{{ - bt_{1} }} - 1} \right)}}{{b^{2} }} + \frac{{at_{1}^{2} }}{{2b}}~} \right\}} \right] \\ & \; - ah_{1} \left[ {\mathop \smallint \limits_{{t_{1} }}^{{t_{2} }} t\left( {\alpha \beta t_{2}^{{\beta - 1~}} - m\left( \xi \right) + b} \right)e^{{ - \left( {\alpha t^{\beta } - m\left( \xi \right)t + bt} \right)}} \cdot e^{{\left( {\alpha t_{2}^{\beta } - m\left( \xi \right)t_{2} + bt_{2} } \right)}} dt + e^{{ - \left( {\alpha t_{2} - m\left( \xi \right)t_{2} + bt_{2} } \right)}} \mathop \smallint \limits_{{t_{1} }}^{{t_{2} }} e^{{\left( {\alpha t^{\beta } - m\left( \xi \right)t + bt} \right)}} \left\{ {~1 - t_{2} \left( {\alpha \beta t_{2}^{{\beta - 1~}} - m\left( \xi \right) + b} \right)} \right\}dt + 2t_{2} } \right] \\ & \; - ah_{2} \left[ {~\mathop \smallint \limits_{{t_{1} }}^{{t_{2} }} \left( {\alpha \beta t_{2}^{{\beta - 1~}} - m\left( \xi \right) + b} \right)e^{{ - \left( {\alpha t^{\beta } - m\left( \xi \right)t + bt} \right)}} \cdot ~e^{{\left( {\alpha t_{2}^{\beta } - m\left( \xi \right)t_{2} + bt_{2} } \right)}} dt - \left( {\alpha \beta t_{2}^{{\beta - 1~}} - m\left( \xi \right) + b} \right) + ~e^{{ - \left( {\alpha t_{2}^{\beta } - m\left( \xi \right)t_{2} + bt_{2} } \right)}} \cdot \mathop \smallint \limits_{{t_{1} }}^{{t_{2} }} e^{{\left( {\alpha t^{\beta } - m\left( \xi \right)t + bt} \right)}} dt + 2~} \right] \\ & \; - \left\{ {ae^{{ - \left( {\alpha t_{1}^{\beta } - m\left( \xi \right)t_{1} + bt_{1} } \right)}} ~\left( {\alpha \beta t_{2}^{{\beta - 1~}} - m\left( \xi \right) + b} \right) + ~e^{{\left( {\alpha t_{2}^{\beta } - m\left( \xi \right)t_{2} + bt_{2} } \right)}} } \right\} \\ & \;a^{2} ~\left[ {~\mathop \smallint \limits_{{t_{1} }}^{{t_{2} }} \left( {\alpha \beta t_{2}^{{\beta - 1~}} - m\left( \xi \right) + b} \right)e^{{ - \left( {\alpha t^{\beta } - m\left( \xi \right)t + bt} \right)}} .~e^{{\left( {\alpha t_{2}^{\beta } - m\left( \xi \right)t_{2} + bt_{2} } \right)}} dt + 1} \right] \\ & \; - \left( {\alpha \beta t_{2}^{{\beta - 1~}} - m\left( \xi \right) + b} \right).e^{{\left( {\alpha t_{2}^{\beta } - m\left( \xi \right)t_{2} + bt_{2} } \right)}} \cdot ~\mathop \smallint \limits_{{t_{1} }}^{{t_{2} }} e^{{\left( {\alpha t^{\beta } - m\left( \xi \right)t + bt} \right)}} dt + 1 \\ & \; - \frac{{i_{c} \omega \sigma \left( {\eta + 1} \right)c_{p} }}{{2\eta }}~\left[ {a\left( {\alpha \beta t_{2}^{{\beta - 1}} - m\left( \xi \right) + b} \right)e^{{ - \left( {\alpha t_{1}^{\beta } - m\left( \xi \right)t_{1} } \right)}} \cdot ~e^{{\left( {\alpha t_{2}^{\beta } - m\left( \xi \right)t_{2} + bt_{2} } \right)}} } \right] \\ \end{aligned} $$

(25)

$$ \frac{{\partial^{2} Z\left( {t_{2} ,t_{3} } \right)}}{{\partial t_{3}^{2} }} = - \frac{{C_{p} a\delta }}{{\left( {1 + \delta t_{3} } \right)^{2} }} + \frac{{C_{b} a}}{{\left( {1 + \delta t_{3} } \right)^{2} }} - \frac{{i_{c} \omega \sigma \left( {\eta + 1} \right)}}{2\eta }\frac{{C_{p} a\delta }}{{\left( {1 + \delta t_{3} } \right)^{2} }} + C_{1} a\left\{ {\frac{\delta }{{\left( {1 + \delta t_{3} } \right)^{2} }} } \right\} $$

(26)

$$ \frac{{\partial^{2} Z\left( {t_{2} ,t_{3} } \right)}}{{\partial t_{3} \partial t_{2} }} = 0 $$

(27)