1 Introduction

The Indian Premier League (IPL) is the most renowned Twenty20 (T20) cricket event in the world, with ten teams competing to be the best team. The league was founded by the Board of Control for Cricket in India (BCCI) in 2007. The first season of the tournament first happened from 18 April to 1 June 2008. There are numerous players from different countries competing for various sides in such a match. The concern is that only a fixed number of players can participate in each match, team management faces a challenge in selecting the ideal player composition. As of right now, neither a foolproof method nor a solution involving the choice of bowlers or batters while keeping experience within the team exist for this problem. In this paper, we are calculating the most suitable player from the available, using distance measure for triangular fuzzy number. A step-by-step algorithm of technique for order preference by similarity to ideal solution is provided for the selection process.

1.1 Literature review

Multi-attribute decision making (MADM) is commonly used in numerous domains, including environmental studies, energy, sustainability management, mathematical modelling and many more. It is an extremely tedious job to obtain precise mathematical value for the examined objects during strategic planning as it involves complexity and ambiguity of human reasoning. MADM is a complex decision-making method that incorporates both quantitative and qualitative elements. To choose the most likely optimal options, several MADM strategies and approaches have been suggested. As an augmentation to the fuzzy MADM approach is suggested in this work, where the rankings of options versus attributes, and the weights of all criteria, are assessed in linguistic values represented by fuzzy numbers. MCDM models under fuzzy environment [15, 16, 24, 29, 34], Intuitionistic fuzzy sets [26], and Pythagorean fuzzy sets [2] have been proposed by several researchers. The set theory related to fuzzy presented is a useful tool for describing circumstances in which information is vague or uncertain. The fuzzy set corresponds to a similar situation by defining the degree to which a particular object belongs to a given set. In fact, however, an individual may assume x to some degree belongs to the set A, but it may be that he is uncertain about it. Fuzzy set theory, a dynamic approach, proposed by Zadeh [59] can be applied in situations involving ambiguity, subjectivity, and vague decisions. Fuzziness characterisation and quantification are critical concerns that influence the management of uncertainty in many information systems and concepts. Biswas et al. [11] proposed a new multi-criteria decision-making (MCDM) framework with spherical fuzzy numbers, trigonometric operators [47], picture fuzzy number [10, 12] and Fermatean fuzzy information [13]. Pamucar et al. [44] developed a novel decision-making approach using Measuring attractiveness through a categorical-based evaluation technique (MACBETH) and a new combinative distance-based assessment method to address the supplier selection problem during the COVID-19 pandemic. Qiyas et al. [46] developed Fractional orthotriple fuzzy rough Hamacher aggregation operators and-their application on service quality of wireless network selection. Unver et al. [52] presented an extended VIseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR) method for solving group decision-making problems. The uncertainties given in the data were handled with the help of the intuitionistic fuzzy valued neutrosophic values (IFVNVs).

The Triangular Fuzzy Number (TFN) can be used in situations where some attribute values need to be expressed objectively to convey the decision-making information. This not only maintains the variable's value in an interval, but also displays the likelihood of different values in the considered interval. Zhang et al. [60] proposed similarity measures for TFN in MADM scenario. Dong et al. [22] discussed fuzzy best-worst technique based on TFN for MCDM approach. Dutta and Dash [23] considered arithmetic of generalized TFN in medical diagnosis. Liu et al. [41] provides a strategy to solve fuzzy multi-attribute decision-making problems denoted by triangular fuzzy numbers based on connection number. Wang and Gong [56] suggested a set-pair analysis-based decision-making technique for solving MADM problems with known criteria weights. The proposed decision-making approach for a black-start ambiguous set by Zhao and Zhang [61] is a theory whose basis is set-pair connection number. Huang and Luo [30] formulated an index weight measure under triangular fuzzy number to evaluate uncertain MADM problem.

The shorter format of cricket, T-20, is India's most popular entertainment sport. The Board for Control of Cricket in India (BCCI) launched the IPL in 2008 with eight franchises. The IPL provides a fantastic opportunity for all cricketers to realize their aspirations. Staden [51] displayed the comparison of performances of batsmen, bowlers, and all-rounders, graphically. Parker et al. [45] calculated the value of players in the IPL. Lemmer proposed several methods for evaluating bowlers and batsmen's performance.

An ideal solution comprises of the optimal values of all criteria whereas, a negative-ideal solution comprises of worst values of all criteria and the selection criteria for alternatives are based on Euclidean distance. The TOPSIS method is easy in implementation and has been applicable in the problems of selection and ranking of alternatives. MCDM methods are popular among the researchers in dealing with decision making problems to get the most reliable alternative. Many researchers [32] analysed MADM approach using Technique for Order of Preference by Similarity to ideal solution (TOPSIS) method. TOPSIS method has been applied in various decision-making problems like supplier selection, selection of land, robotics, medical diagnosis, ranking of water quality, human resource selection personnel problem, and many other real-life situations flavoured with fuzzy sets and generalized fuzzy sets [1, 3, 4, 6,7,8,9, 14, 17,18,19, 25, 27, 31, 35,36,37,38,39,40,41,42,43, 49, 53, 55, 57, 58]. Gupta et al. [28] proposed a hybrid fuzzy decision-making framework for the analysis of COVID-19. The study contributed to the discipline of decision analytics and healthcare risk management. Salih et al. [50] mapped the research landscape of Fuzzy-TOPSIS into a coherent taxonomy and highlighted the open challenges that hinder the of develop the Fuzzy-TOPSIS. Alaa et al. [5] proposed a novel methodology for evaluating and ranking pre-service teachers' English proficiency based on multi-criteria analysis and fuzzy Delphi. There were three experiments done. First, using the Delphi technique, criteria were derived from the literature review and the insights of representative experts. Second, 31 pre-service teachers were assessed to ascertain their abilities based on the results of the Delphi criterion. The English Language Testing Service and four language skill exams were used to assess English ability. Experts with extensive experience in English education analysed each exam. Thirdly, pre-service instructors were ranked using TOPSIS approach in accordance with a set of verified Delphi criteria results. Rathore and Gupta [48] proposed a hybrid fuzzy-based decision-making framework to rank the Indian hospitals based on the prevalence of safety risk factors among the health care workers during COVID 19 pandemic. Zughoul et al. [62] presented a novel triplex procedure for ranking the ability of software engineering students to address the literature gap. The methodology of the proposed work is presented based on three phases: Identification, pre-processing, and development phase. Study of Inani and Gupta [33] evaluated the financial performance of nine information technology firms, listed in National Stock Exchange of India, for a period of 5 years. Ten commonly used financial measurements were utilized as numerous criteria in the TOPSIS technique to rank the companies based on their financial performance.

1.2 Motivation of the study

For the linguistic assessments, the technique of classical TOPSIS is used, but due to the uncertainty and imprecise nature of the linguistic assessments, we proposed distance measures for triangular fuzzy numbers under TOPSIS approach.

Summarizing the existing literature in the field, we observe that majority of the distance measures are introduced as a generalization of fuzzy sets. Most of the measures do not cater the process of normalization and hence provides results that are not realistic to decision making problems. Existing distance measures do not serve a powerful mathematical tool to handle complex problems. Additionally, existing measures do not clearly distinguish between highly uncertain TFN with very low membership and non-membership grade values. When there is little information or expertise available about a system, one confronts such TFNs. Therefore, proper distance measures are required to handle such TFNs. The significant contributions of this study are

  • Novel distance measure for triangular fuzzy numbers to depict the degree of fuzziness is introduced.

  • A new triangular fuzzy MCDM approach based on distance measures is discussed.

  • For improving the efficiency of the suggested measures, sensitivity is also presented.

  • The results of proposed distance measures shows that our model work efficiently and effectively.

1.3 Structure of article

The article is organized as follows: Sect. 2 delves into the fundamental terminologies which will be helpful in performance evaluation. In the 3rd section, we propose novel distance measures proving its validity through axiomatic approach. TOPSIS algorithm and the procedure to find the ranking of players has been discussed in Sect. 4. Section 5 gives a real-life example of selecting best all-rounder cricket player through these distance measures for TFNs under TOPSIS. Section 6 presents the comparative study of the developed measures with the existing ones. Finally, Sect. 7 concluded the article.

2 Preliminaries

In this segment, we bring in some fundamental theories associated to FSs [44, 47, 48], TFN, similarity measure and distance measure used in the study.

Definition 2.1

Zadeh [59]. A fuzzy set \(\mathcal{M}\) in \(\mathrm{\mho }\) is characterized by a membership function:

$$\mathcal{M}=\left\{\langle \mathrm{u}, {\updelta }_{\mathcal{M}}(\mathrm{u})\rangle \left|\mathrm{u}\in \mathrm{\mho }\right.\right\}$$
(1)

where \({\updelta }_{\mathcal{M}}(\mathrm{u}):\mathrm{\mho }\to \left[0, 1\right]\) is a measure of belongingness of degree of participation of an element \(\mathrm{u}\in \mathrm{\mho }\) in \(\mathcal{M}\).

Definition 2.2

Hung and Chen [21]. Let \(\mathcal{M}=[\mathrm{a},\mathrm{ b},\mathrm{ c},\mathrm{ d}]\) be a real fuzzy number, the membership function of which can be expressed as

$${{\delta }}_{{\mathcal{M}}} \left( x \right) = \left\{ {\begin{array}{ll} {{{\delta }}_{{\mathcal{M}}}^{L} \left( x \right),} &\quad {a \le x \le b} \\ {1,} &\quad {b \le x \le c} \\ {{{\delta }}_{{\mathcal{M}}}^{U} \left( x \right),} &\quad {c \le x \le d} \\ {0,} & \quad {otherwise} \\ \end{array} } \right.$$
(2)

where \({\updelta }_{\mathcal{M}}^{L}(x)\) and \({\updelta }_{\mathcal{M}}^{U}(x)\) are the lower and upper membership functions of fuzzy number \(\mathcal{M}\), respectively and \(\mathrm{a}=-\infty\), or \(\mathrm{a}=\mathrm{b}\), or \(\mathrm{b}=\mathrm{c}\), or \(\mathrm{c}=\mathrm{d}\), or \(\mathrm{d}=+\infty\).

Definition 2.3

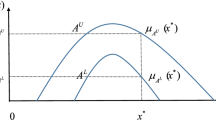
Zhang et al. [60] and Zhao and Zhang [61]. A triangular fuzzy number \(\mathcal{M}\) is a fuzzy number with piecewise linear membership function \({\updelta }_{\mathcal{M}}\) defined by.

$${\updelta }_{\mathcal{M}}=\left\{\begin{array}{ll}\frac{x-{a}_{1}}{{a}_{2}-{a}_{1}},&\quad {a}_{1}\le x\le {a}_{2}\\ \frac{{a}_{3}-x}{{a}_{3}-{a}_{2}},&\quad {a}_{2}\le x\le {a}_{3}\\ 0,&\quad otherwise\end{array}\right.$$
(3)

which can be denoted as \(({a}_{1}, {a}_{2}\), \({a}_{3}).\) Graphical representation can be depicted by Fig. 1, as follows:

Fig. 1
figure 1

Triangular Fuzzy Number

Full size image

Let \(\wp =({x}_{1}, {x}_{2}, {x}_{3})\) and \({\mathbb{Q}}=({y}_{1}, {y}_{2}, {y}_{3})\) be two TFNs and \(\alpha\) a positive number then the basic operations are as follows:

$$\mathbb{\wp }\oplus {\mathbb{Q}}=\left({x}_{1}+{y}_{1}, {x}_{2}+{y}_{2}, {x}_{3}+{y}_{3}\right),$$
$$\mathbb{\wp }\otimes {\mathbb{Q}}=\left({x}_{1}{y}_{1}, {x}_{2}{y}_{2}, {x}_{3}{y}_{3}\right),$$
$$\alpha \otimes \wp =\left({\alpha x}_{1}, {\alpha x}_{2}, {\alpha x}_{3}\right),$$
$$\frac{1}{\wp }=\left(\frac{1}{{x}_{1}}, \frac{1}{{x}_{2}}, \frac{1}{{x}_{3}}\right)$$

Definition 2.4

Let \(P=({x}_{1}, {x}_{2}\), \({x}_{3})\) and \(Q=({y}_{1}, {y}_{2}\), \({y}_{3})\) be two TFNs. Then, distance measure function \(D\left(P, Q\right)\) can be defined [20] as

$$D\left(P, Q\right)=\sqrt{\frac{1}{3}\left\{{({y}_{1}-{x}_{1})}^{2}+{({y}_{2}-{x}_{2})}^{2}+{({y}_{3}-{x}_{3})}^{2}\right\}}$$
(4)

Definition 2.5

Zhang et al. [60]. Let \(P=({x}_{1}, {x}_{2}\), \({x}_{3})\) and \(Q=({y}_{1}, {y}_{2}\), \({y}_{3})\) be two TFNs. Then, similarity measure function \(S\left(\mathbb{\wp },{\mathbb{Q}}\right)\) can be defined [18] as.

$$S\left(\mathbb{\wp },{\mathbb{Q}}\right)=\frac{\sum_{i=1}^{3}{x}_{i}{y}_{i}}{2\sum_{i=1}^{3}{x}_{i}^{2}+2\sum_{i=1}^{3}{y}_{i}^{2}-\sum_{i=1}^{3}{x}_{i}{y}_{i}}$$
(5)

3 Distance measures for triangular fuzzy numbers

Firstly, we reminiscence the self-evident definition of distance measure for TFNs.

Proposition 1

Let \(\mathrm{\rm X}\) be nonempty set and P, Q, R ∈ PFS (\(\mathrm{\rm X}\)). The distance measure between P and Q is a function \(Div:TFN \times TFN\to \left[0, 1\right]\) satisfies.

  1. (P1)

    Boundedness:\(0\le Div\left(\wp , {\mathbb{Q}}\right)\le 1\)

  2. (P2)

    Separability: If \(\wp = {\mathbb{Q}}\), i.e., \({x}_{i}={y}_{i};i-=1, 2, 3\), then \(Div\left(\wp , {\mathbb{Q}}\right)=0\).

  3. (P3)

    Symmetric:\(Div\left(\wp , {\mathbb{Q}}\right)= Div\left({\mathbb{Q}},\mathbb{\wp } \right).\)

Let \(\wp , {\mathbb{Q}}\in\) TFN (\(\mathrm{\rm X})\) such that \(\wp =\left\{{x}_{1}, {x}_{2}, {x}_{3}\right\}\) and \({\mathbb{Q}}=\left\{{y}_{1}, {y}_{2}, {y}_{3}\right\}\) then

$${D}_{TFN1}\left(\wp , {\mathbb{Q}}\right)=1-\frac{\sum_{i=1}^{3}{x}_{i}{y}_{i}({x}_{i}{+y}_{i})}{2\sum_{i=1}^{3}{x}_{i}^{3}+2\sum_{i=1}^{3}{y}_{i}^{3}-\sum_{i=1}^{3}{x}_{i}{y}_{i}({x}_{i}{+y}_{i})}$$
(6)

In several circumstances, the weight of the elements must be considered. For instance, in decision making, the attributes usually have distinct significance, and thus ought to be designated unique weights. In extension to the results obtained, we propose fuzzy entropy for PFSs as follows:

$${D}_{WTFN}\left(\wp , {\mathbb{Q}}\right)=1-\sum_{j=1}^{3}{\omega }_{j}\left\{\frac{\sum_{i=1}^{3}{x}_{i}{y}_{i}({x}_{i}{+y}_{i})}{2\sum_{i=1}^{3}{x}_{i}^{3}+2\sum_{i=1}^{3}{y}_{i}^{3}-\sum_{i=1}^{3}{x}_{i}{y}_{i}({x}_{i}{+y}_{i})}\right\}$$
(7)

where \(\omega\) is the weight vector with \({\omega }_{j}\in \left[0, 1\right], j=1, 2, 3, \sum_{j=1}^{3}{\omega }_{k}=1\). If we take \({\omega }_{j}=1, k=1, 2, 3\), then \({D}_{WTFN1}\left(\mathrm{\wp }, {\mathbb{Q}}\right)={D}_{TFN1}\left(\mathrm{\wp }, {\mathbb{Q}}\right).\)

Theorem 3.1

The distance measures for triangular fuzzy numbers defined in Eqs. (6–7) are valid measures of TFNs.

Proof

All the necessary four conditions to be an entropy measure are satisfied by the new measures as follows:

  1. (D1)

    Boundedness: \(0\le {D}_{TFN1}\left(\mathrm{\wp }, {\mathbb{Q}}\right), {D}_{WTFN1}\left(\mathrm{\wp }, {\mathbb{Q}}\right)\le 1\)

Proof

By the definition of TFNs, we have \(\frac{\sum_{i=1}^{3}{x}_{i}{y}_{i}({x}_{i}{+y}_{i})}{2\sum_{i=1}^{3}{x}_{i}^{3}+2\sum_{i=1}^{3}{y}_{i}^{3}-\sum_{i=1}^{3}{x}_{i}{y}_{i}({x}_{i}{+y}_{i})}\ge 0\). Hence, we need to prove that \(\frac{\sum_{i=1}^{3}{x}_{i}{y}_{i}({x}_{i}{+y}_{i})}{2\sum_{i=1}^{3}{x}_{i}^{3}+2\sum_{i=1}^{3}{y}_{i}^{3}-\sum_{i=1}^{3}{x}_{i}{y}_{i}({x}_{i}{+y}_{i})}\le 1\).

Using mathematical inequalities, we have

$${x}_{i}^{3}+{y}_{i}^{3}\ge {x}_{i}{y}_{i}({x}_{i}{+y}_{i}) \Rightarrow 2\sum_{i=1}^{3}{x}_{i}^{3}+2\sum_{i=1}^{3}{y}_{i}^{3}\ge \sum_{i=1}^{3}{x}_{i}{y}_{i}({x}_{i}{+y}_{i})$$

\(\Rightarrow 2\sum_{i=1}^{3}{x}_{i}^{3}+2\sum_{i=1}^{3}{y}_{i}^{3}-\sum_{i=1}^{3}{x}_{i}{y}_{i}({x}_{i}{+y}_{i})\ge 0\), or

\(\frac{\sum_{i=1}^{3}{x}_{i}{y}_{i}({x}_{i}{+y}_{i})}{2\sum_{i=1}^{3}{x}_{i}^{3}+2\sum_{i=1}^{3}{y}_{i}^{3}-\sum_{i=1}^{3}{x}_{i}{y}_{i}({x}_{i}{+y}_{i})}\le 1\). Hence, \(0\le {D}_{TFN1}\left(\mathrm{\wp }, {\mathbb{Q}}\right)\le 1\)

Measure \({D}_{WTFN}\left(\wp , {\mathbb{Q}}\right)\) can be proved similarly.

  1. (D2)

    Separability: \(\mathrm{\wp }= {\mathbb{Q}}\Rightarrow {D}_{TFN1}\left(\mathrm{\wp }, {\mathbb{Q}}\right), {D}_{WTFN1}\left(\mathrm{\wp }, {\mathbb{Q}}\right)=0\)

Proof

If \(\wp = {\mathbb{Q}}\), then \({D}_{TFN1}\left(\wp , {\mathbb{Q}}\right)=1-\frac{\sum_{i=1}^{3}{x}_{i}{x}_{i}({x}_{i}{+x}_{i})}{2\sum_{i=1}^{3}{x}_{i}^{3}+2\sum_{i=1}^{3}{x}_{i}^{3}-\sum_{i=1}^{3}{x}_{i}{x}_{i}({x}_{i}{+x}_{i})}\)

\(\Rightarrow 1-1=0\).

Measure \({D}_{WTFN}\left(\wp , {\mathbb{Q}}\right)\) can be proved similarly.

  1. (D3)

    Symmetric: \(Div\left(\mathrm{\wp }, {\mathbb{Q}}\right)= Div\left({\mathbb{Q}},\mathrm{ \wp }\right).\)

It is evident from the measure.

Measure \({D}_{WTFN}\left(\wp , {\mathbb{Q}}\right)\) can be proved similarly.

4 Proposed methodology

When standard quantitative concepts are difficult or inadequately defined, the idea of linguistic variables is employed to provide approximate characterization. This segment presents MADM issue under fuzzy environment. A viable dynamic methodology is proposed to manage such MCDM issues. Each decision matrix in MADM techniques has four main components as (a) criteria, (b) alternatives, (c) weight or relative importance of each attribute and (d) assessment value of alternatives with respect to the criteria. An algorithm of the proposed technique is too introduced which will be applied in selection procedure of all-rounder cricket player in this session (Fig. 2).

  • Step 1 Construct a decision matrix \({\hat{\mathbf{D}}}_{{\varvec{i}}{\varvec{j}}}\) with the performance ratings of each alternative for criteria used in the evaluation procedure, as follows:

    $${{\varvec{D}}}_{{\varvec{i}}{\varvec{j}}}=\left[\begin{array}{cccc}{{\varvec{d}}}_{11}& {{\varvec{d}}}_{12}& \dots & {{\varvec{d}}}_{1{\varvec{n}}}\\ {{\varvec{d}}}_{21}& {{\varvec{d}}}_{22}& \dots & {{\varvec{d}}}_{2{\varvec{n}}}\\ \dots & \dots & \dots & \dots \\ {{\varvec{d}}}_{{\varvec{m}}1}& {{\varvec{d}}}_{{\varvec{m}}2}& \dots & {{\varvec{d}}}_{{\varvec{m}}{\varvec{n}}}\end{array}\right]$$
    (8)

    where \({\varvec{i}}=1,2,\dots {\varvec{m}}\) and \({\varvec{j}}=1,2,\dots {\varvec{n}}\) shows the alternatives and criteria.

  • Step 2 Gather subjective opinion of the decision makers on significance of weights as shown in Table 1:

    Table 1 Linguistic Variables [54] and their corresponding Triangular Fuzzy Weights
    Full size table

  • Step 3 Compute weights using the following equations:

    $$\left.\begin{array}{c}{{\varvec{\omega}}}_{{\varvec{j}}1}=\underset{{\varvec{k}}}{\mathbf{min}}\left\{{{\varvec{\omega}}}_{{\varvec{j}}1}^{{\varvec{k}}}\right\}\\ {{\varvec{\omega}}}_{{\varvec{j}}2}=\frac{1}{{\varvec{K}}}\sum_{{\varvec{k}}=1}^{{\varvec{K}}}{{\varvec{\omega}}}_{{\varvec{j}}2}^{{\varvec{k}}}\\ {{\varvec{\omega}}}_{{\varvec{j}}3}=\underset{{\varvec{k}}}{\mathbf{max}}\left\{{{\varvec{\omega}}}_{{\varvec{j}}3}^{{\varvec{k}}}\right\}\end{array}\right\}$$
    (9)

  • Step 4 Form a fuzzy weighted decision matrix by multiplying the normalized decision matrix with corresponding fuzzy weight:

    $$\overbrace {{\varvec{V}}} = \left[ {\begin{array}{*{20}c} {{\varvec{v}}_{11} } & {{\varvec{v}}_{12} } & \ldots & {{\varvec{v}}_{{1{\varvec{n}}}} } \\ {{\varvec{v}}_{21} } & {{\varvec{v}}_{22} } & \ldots & {{\varvec{v}}_{{2{\varvec{n}}}} } \\ \ldots & \ldots & \ldots & \ldots \\ {{\varvec{v}}_{{{\varvec{m}}1}} } & {{\varvec{v}}_{{{\varvec{m}}2}} } & \ldots & {{\varvec{v}}_{{{\varvec{mn}}}} } \\ \end{array} } \right]$$
    (10)

    where \({\varvec{i}}=1, 2, \dots {\varvec{m}}\) and \({\varvec{j}}=1, 2, \dots {\varvec{n}}\) and \({{\varvec{v}}}_{{\varvec{i}}{\varvec{j}}}=({{\varvec{w}}}_{{\varvec{j}}1}{{\varvec{d}}}_{1{\varvec{j}}}, {{\varvec{w}}}_{{\varvec{j}}2}{{\varvec{d}}}_{2{\varvec{j}}}, {{\varvec{w}}}_{{\varvec{j}}3}{{\varvec{d}}}_{3{\varvec{j}}})\)

  • Step 5 The coordinates for the fuzzy positive ideal solution (FPIS) and fuzzy negative ideal solution (FNIS) are

    $$A^{(k + )} = v_{1}^{(k + )} ,v_{2}^{(k + )} , \ldots ,v_{n}^{(k + )} = \left\{ {\left( {\mathop {\max }\limits_{i} (v_{ij}^{k} )/j \in B} \right),\;\left( {(\mathop {\min }\limits_{i} (v_{ij}^{k} )/j \in C)} \right)} \right\}$$
    (11)
    $${\text{and}}\;\mathbf{A}^{{\mathbf{k} - }} = \left\{ {\mathbf{v}_{1}^{{\mathbf{k} - }} ,~\mathbf{v}_{2}^{{\mathbf{k} - }} , \ldots ,~\mathbf{v}_{\mathbf{n}}^{{\mathbf{k} - }} } \right\} = \left\{ {\left( {\mathop {\min }\limits_{\mathbf{i}} \left( {\mathbf{v}_{{\mathbf{ij}}}^{\mathbf{k}} } \right)\mathbf{/j} \in \mathbf{C}} \right),\left( {\left( {\mathop {\max }\limits_{\mathbf{i}} \left( {\mathbf{v}_{{\mathbf{ij}}}^{\mathbf{k}} } \right)\mathbf{/j} \in \mathbf{B}} \right)} \right)} \right\}$$
    (12)

    where B is the benefit criteria and C is the cost criteria.

  • Step 6 The distance of each alternative from FPIS and FNIS is calculated as.

    $${{\varvec{S}}}_{{\varvec{i}}}^{+}=\sum_{{\varvec{i}}=1}^{{\varvec{n}}}{\varvec{D}}\left({{\varvec{A}}}_{{\varvec{i}}}, {{\varvec{A}}}^{{\varvec{k}}+}\right)$$

    and \({{\varvec{S}}}_{{\varvec{i}}}^{-}=\sum_{{\varvec{i}}=1}^{{\varvec{n}}}{\varvec{D}}\left({{\varvec{A}}}_{{\varvec{i}}},{{\varvec{A}}}^{{\varvec{k}}-}\right)\),

    $${\varvec{D}}\left({{\varvec{A}}}_{{\varvec{i}}},{{\varvec{A}}}^{{\varvec{k}}-}\right)=\frac{\sum_{{\varvec{i}}=1}^{3}{{\varvec{x}}}_{{\varvec{i}}}{{\varvec{y}}}_{{\varvec{i}}}^{-}({{\varvec{x}}}_{{\varvec{i}}}+{{\varvec{y}}}_{{\varvec{i}}}^{-})}{2\sum_{{\varvec{i}}=1}^{3}{{\varvec{x}}}_{{\varvec{i}}}^{3}+2\sum_{{\varvec{i}}=1}^{3}{{\varvec{y}}}_{{\varvec{i}}}^{3-}-\sum_{{\varvec{i}}=1}^{3}{{\varvec{x}}}_{{\varvec{i}}}{{\varvec{y}}}_{{\varvec{i}}}^{-}({{\varvec{x}}}_{{\varvec{i}}}+{{\varvec{y}}}_{{\varvec{i}}}^{-})}$$
    (14)

  • Step 7 The closeness coefficient \({{\varvec{R}}}_{{\varvec{i}}}\) of the alternatives are calculated as

    $${{\varvec{R}}}_{{\varvec{i}}}=\frac{\sum_{{\varvec{i}}=1}^{{\varvec{n}}}{\varvec{D}}\left({{\varvec{A}}}_{{\varvec{i}}},{{\varvec{A}}}^{{\varvec{k}}-}\right)}{\sum_{{\varvec{i}}=1}^{{\varvec{n}}}{\varvec{D}}\left({{\varvec{A}}}_{{\varvec{i}}},{{\varvec{A}}}^{{\varvec{k}}+}\right)+\sum_{{\varvec{i}}=1}^{{\varvec{n}}}{\varvec{D}}\left({{\varvec{A}}}_{{\varvec{i}}},{{\varvec{A}}}^{{\varvec{k}}-}\right)}=\frac{{{\varvec{S}}}_{{\varvec{i}}}^{-}}{{{{\varvec{S}}}_{{\varvec{i}}}^{+}+{\varvec{S}}}_{{\varvec{i}}}^{-}}$$
    (15)

    where \(0\le {{\varvec{R}}}_{\mathbf{i}}\le 1, {\varvec{i}}=1, 2, \dots , {\varvec{m}}\)

  • Step 8 Rank the alternatives according to their closeness coefficient so that the higher value being the best ideal solution.

Fig. 2
figure 2

Algorithm for TOPSIS approach

Full size image

5 Case study

In cricket we have players who are either batsmen or bowlers or all-rounders. An all-rounder, in cricket, is a player who performs well in both bowling as well as batting. This paper is aimed at ranking of all-rounder cricket players and selection of the best all-rounder from the pool of considered (five) all-rounders. The franchise owners of IPL twenty-20 cricket tournament usually choose their players through auction and on the individual past performance of players. For proper bidding, each player's price is determined by their individual performances, and franchisee owners receive the complete picture and choose their right team with appropriate players, resulting in a significantly higher profit from the IPL T-20 event. In T-20 cricket, the all-rounder plays a considerably larger role than other category players, be it bowlers or batsmen. Data including batting average (C1), batting strike-rate (C2), bowling average (C3) and bowling strike-rate (C4) has been collected from https://www.cricbuzz.com/profiles for the current study as shown in Table 2.

Table 2 Data Set in the form of decision matrix
Full size table

This real data has been collected from premierleaguecricket.in. Based on this data we must take a decision whether which player to buy. Now the first think in the MADM is to classify the problem that we have in the form of benefit and cost criteria. Benefit criteria are those where higher values are desired and cost criteria are those where low values are required. Here, C1 and C2 are benefit criteria where C3 and C4 are cost criteria. The first thing which we need to choose the 7-point scale of triangular fuzzy number as shown in Table 4. Let there be four decision makers Owner (DM1), Captain (DM2), Coach (DM3) and Sponsor (DM4). These four persons will decide regarding the all-rounder cricket player. The decision maker’s choice in terms of linguistic variables can be depicted in Table 3. Fuzzy weights, based on the decision maker’s subjective evaluations, are calculated, as shown below in Table 4. Next, we will find the aggregative fuzzy weight using Eq. 9 by taking the four values for the upper, medium, and lower values as shown in Table 5. We compute weighted normalized decision matrix (Table 6) by multiplying the normalized decision matrix with corresponding fuzzy weights using the formula \(\overbrace {{\varvec{V}}} = {\varvec{d}}_{{{\varvec{ij}}}} \times \user2{ w}_{{{\varvec{ij}}}} .\) Identify the fuzzy positive ideal solution (PIS) and fuzzy negative ideal solution (NIS) using Eq. (11) and (12) as shown in Table 7.

Table 3 Rating criteria on a linguistic scale by decision makers
Full size table
Table 4 Conversion of linguistic ratings of decision makers into quantitative values
Full size table
Table 5 Calculation of aggregative fuzzy weights
Full size table
Table 6 Fuzzy weighted normalized decision matrix
Full size table
Table 7 Positive and Negative Ideal values for each criterion
Full size table

The distance of each alternative from fuzzy positive ideal values and from negative ideal values, is calculated using Eqs. (13–14) and shown in Tables 8 and 9.

Table 8 Separation measures for fuzzy positive Ideal solutions (FPIS) for each criterion
Full size table
Table 9 Separation measures for fuzzy negative Ideal solutions (FNIS) for each criterion
Full size table

The closeness coefficients (\({{\varvec{R}}}_{{\varvec{i}}})\) of each considered alternative is calculated using Eq. (15) and ranked in decreasing order (shown in Table 10) as.

Table 10 Ranking result obtained from TOPSIS approach
Full size table

5.1 Sensitivity analysis

If decision makers find distinct ranking for the alternatives, the overall findings of the best alternatives remain unclear. To reduce the vagueness about the best option with respect to the decision-makers, various values of the experts are accumulated by assigning a priority value \({\varvec{\rho}}={({{\varvec{\rho}}}_{1},\boldsymbol{ }\boldsymbol{ }{{\varvec{\rho}}}_{2},\boldsymbol{ }\dots ,\boldsymbol{ }{{\varvec{\rho}}}_{{\varvec{k}}})}^{{\varvec{T}}}\) to each expert such that \({{\varvec{\rho}}}_{{\varvec{k}}}>0\) and \(\sum_{{\varvec{k}}=1}^{{\varvec{K}}}{{\varvec{\rho}}}_{{\varvec{k}}}=1\). The distance measure of each expert is aggregated by using these weight vectors and the overall measurement values of the alternatives are obtained that can be depicted in Table 11 (a), (b), (c) and (d) as follows:

$${\boldsymbol{\vartheta }}_{{\varvec{i}}}^{+}=\sum_{{\varvec{k}}=1}^{{\varvec{s}}}{{\varvec{\rho}}}_{{\varvec{k}}}{{\varvec{C}}}_{{\varvec{i}}{\varvec{j}}}^{+}$$
(16)
$${\text{and}}\;\vartheta_{{\varvec{i}}}^{ - } = \mathop \sum \limits_{{{\varvec{k}} = 1}}^{{\varvec{s}}} {\varvec{\rho}}_{{\varvec{k}}} {\varvec{C}}_{{{\varvec{ij}}}}^{ - }$$
(17)
$${\text{Also}},\;{\mathbf{\Re }}_{{\varvec{i}}} = \user2{ }\frac{{\vartheta_{{\varvec{i}}}^{ - } }}{{\vartheta_{{\varvec{i}}}^{ + } + \vartheta_{{\varvec{i}}}^{ - } }}\user2{ }$$
(18)

where \(0\le {\mathfrak{R}}_{{\varvec{i}}}\le 1, {\varvec{i}}=1, 2, \dots , 5\)

Table 11 Aggregated closeness coefficient and ranking for each candidate
Full size table

Ranking of players using sensitivitity analysis can be depicted graphically in Fig. 3.

Fig. 3
figure 3

Ranking of players using sensitivity analysis

Full size image

6 Conclusion

The distance measure is an effective method to solve the fuzzy multi attribute decision making problem, but it is rarely applying to triangular fuzzy MADM problem. In this article, this innovative approach is used to measure the performance of all-rounder cricket players, ensuring that the results are accurate every time. Comparison between alternatives or characteristics that uses fuzzy membership tackles the uncertainty and erroneous judgement. By using the TOPSIS approach, this paper presents study in MADM under a fuzzy TOPSIS environment. Because of its capacity to accommodate decision maker’s vague opinions and perceptions, the TOPSIS method has been shown to be the best way for tackling MADM challenges. A closeness coefficient of each alternative is used to determine the ranking order of all alternatives. The higher value of the closeness coefficient indicates that an alternative is closer to FPIS and farther from FNIS simultaneously. The application of fuzzy set theory in conjunction with TOPSIS is effective to provide a more realistic solution to the process of decision making. Therefore, the implementation of fuzzy TOPSIS in this scenario is effective in real-world applications. The proposed method is very appropriate when dealing with a subjective assessment of the real environment that is full of uncertainties. This novel model assists decision makers in making error-free decisions in a methodical manner, regardless of the multi-criteria field. The concept of TOPSIS can be applied to solve real life problems in fuzzy environments, which have uncertainty problems associated with them. One of the tools that helps decision makers with more than just a solution to an issue is sensitivity analysis. It gives an idea of the issues with the model. Finally, the decision maker has a good notion of how sensitive the optimal solution is, by changing one or more parameters' input values. This article takes into consideration sensitivity analysis which shows that our proposed method is effective. The limitation of this study is lack of machine learning which can do the fuzzification that is needed to convert raw data into triangular fuzzy numbers. In future, the study can be extended to incorporate more decision-making techniques like, AHP, COPRAS, VIKOR in real life situations to deal with uncertainty.

In future, the application of our proposed distance measures needs to be extended for Pythagorean fuzzy sets, Fermatean fuzzy sets, etc. Instead of TOPSIS, the work can be further improved in future for various other approaches such as VIKOR, AHP, ELECTRE, PROMETHEE to solve real life MCDM problems. Additionally, we will show the applicability of the suggested distance measures for pattern recognition, clustering, medical analysis, risk analysis, IoT and cloud computing under triangular fuzzy environment.