Introduction

Internet bottleneck is a growing problem in the telecommunication industry [1,2,3,4,5,6,7,8,9,10,11,12]. This is one of the features from telecommunication industry that needs to be addressed right away. It is imperative that the suppression of such a feature is an absolute necessity for performance enhancement of soliton transmission across intercontinental distances. There are several measures and means that have been proposed that can mitigate this effect. A few of such approaches are the consideration of time-dependent coefficients of chromatic dispersion (CD) and self-phase modulation (SPM), introduction of spatio-temporal dispersion in addition to the pre-existing CD and finally generalizing the linear temporal evolution to fractional temporal evolution. The current paper will address the study of optical solitons using the third approach with linear CD. However, the SPM structure will be the one that was proposed by Kudryashov that contains the power-law parameter to be n. The Kudryashov’s approach is the integration algorithm adopted in the current work that would yield soliton solutions with te fractional temporal evolution parameter embedded in them.

Kudryashov, in [13], introduced an innovative nonlinear refractive index model, which offers a thorough framework for analyzing pulse propagation in nonlinear optics. Yildirim et al. [14] utilize various integration schemes to derive multiple soliton solutions for Kudryashov’s type of arbitrary refractive index. Zayed et al. achieved the derivation of soliton solutions through the integration of Kudryashov’s sextic power-law nonlinearity into the refractive index. Employing three unique integration algorithms, they elucidated the criteria governing the existence of these solitons [15]. Recently, Xu [16] introduced exact chirped solutions for the current model by employing the complete discriminant system for the polynomial method and the trial equation method. Furthermore, Zhang utilized the entire discrimination system and the trial equation approach to produce a range of distinct optical wave patterns within the present model. Numerous innovative adaptations of self-phase modulation (SPM) have also been proposed [17,18,19]. The optical soliton solutions for the current model with third-order dispersion and fourth-order dispersion are studied in [20]. In this study, the conformable nonlinear Schrödinger equation is considered, with Kudryashov’s generalized form of the refractive index given as follows [21]:

Governing model

The governing nonlinear Schrödinger’s equation (NLSE) with fractinal temporal evolution, linear CD and Kudryashov’s form of SPM reads:

$$\begin{aligned}{} & {} i\frac{{{\partial }^{\alpha }}q}{\partial {{t}^{\alpha }}}+a{{q}_{xx}}+\left( \frac{{{b}_{1}}}{{{\left| q \right| }^{4n}}}+\frac{{{b}_{2}}}{{{\left| q \right| }^{3n}}}+\frac{{{b}_{3}}}{{{\left| q \right| }^{2n}}}+\frac{{{b}_{4}}}{{{\left| q \right| }^{n}}}\right. \nonumber \\{} & {} \qquad \left. +{{b}_{5}}{{\left| q \right| }^{n}}+{{b}_{6}}{{\left| q \right| }^{2n}}+{{b}_{7}}{{\left| q \right| }^{3n}}+{{b}_{8}}{{\left| q \right| }^{4n}} \right) q \nonumber \\{} & {} \quad = i\left[ \lambda {{(q{{\left| q \right| }^{2m}})}_{x}}+\theta {{({{\left| q \right| }^{2m}})}_{x}}q+\mu {{q}_{x}}{{\left| q \right| }^{2m}} \right] , \end{aligned}$$
(1)

for \(0 < \alpha \le 1\). In the above equation, t signifies temporal variables while x denotes spatial variables. Here, n and m are the power nonlinearity parameter and arbitrary intensity. The coefficient a is the chromatic dispersion and \({{b}_{i}},\,i=1,...,8\) are the nonlinearity coefficients. Further, the coefficients \(\mu\) and \(\theta\)represent the nonlinearity dispersion and the higher order coefficients, respectively. \(\frac{{{\partial }^{\alpha }}(.)}{\partial {{t}^{\alpha }}}\) is the conformable derivative. Here, we explore the core principles of conformable derivatives, laying the foundation for comprehending the dynamics of a wide range of physical phenomena. The utilization of conformable derivatives spans diverse disciplines such as physics, engineering, finance, and biology, underscoring its significant utility as an invaluable instrument for dissecting intricate systems [22, 23]. The present model with fourth order dispersion and third order dispersion using improved modified extended tanh method was studied by Samir et al. [24]. Cubic-quartic exact solutions for the Kudryashov law, featuring a dual form of generalized nonlocal nonlinearity are constructed in [25]. In [21], two powerful methods used to construct the soliton spectrum to a nonlinear Schrödinger equation with refractive index.

The innovative method introduced by the Russian mathematician Kudryashov in 2020 [26, 27], known as the Kudryashov approach, has gained considerable traction among researchers. It has been extensively utilized to generate optical soliton solutions for differential equations of integer and fractional orders [28, 29].

The purpose of this study is to advance the boundaries of research in the field by introducing a range of innovative optical solutions tailored for the conformable nonlinear Schrödinger equation. Our primary emphasis lies in the integration of Kudryashov’s arbitrary refractive index concept with two unique nonlocal nonlinearities, capitalizing on the effectiveness of the Kudryashov technique.

Definition 1.1

Let \(q:(0,\infty )\rightarrow R\). The conformable derivative of order \(\theta\) can be introduced as follows:

$$\begin{aligned} {{L}_{\theta }}\left( q \right) (x)=\underset{a\rightarrow 0}{\mathop {\lim }}\,\frac{q(x+a{{x}^{1-\theta }})-q(x)}{a}, \end{aligned}$$
(2)

for all \(x>0\) and \(\theta \in (0,1]\) [30].

Kudryashov’s approach: A quick glance

The proposed technique utilizes a unique function specifically crafted to adeptly manage the complexities and requirements involved in deriving optical soliton solutions. This innovative method relies on the utilization of the subsequent functions:

$$\begin{aligned} F(\varsigma )=\frac{4{{\vartheta }_{1}}}{\left( \vartheta _{2}^{2}\pm 4{{\vartheta }_{1}}{{\vartheta }_{3}} \right) {{e}^{r\sqrt{{{\vartheta }_{1}}}\varsigma }}\mp 2{{\vartheta }_{2}}+{{e}^{-r\sqrt{{{\vartheta }_{1}}}\varsigma }}}. \end{aligned}$$
(3)

The following hyperbolic function is equivalent to the above function:

$$\begin{aligned} F(\varsigma )=\pm \frac{{{\vartheta }_{1}}{{\vartheta }_{2}}{{\left( {\text {sech}}\left( \frac{\varepsilon r\varsigma }{2}\sqrt{{{\vartheta }_{1}}} \right) \right) }^{2}}}{\vartheta _{2}^{2}\pm {{\vartheta }_{1}}{{\vartheta }_{3}}{{\left( 1-\tanh \left( \frac{\varepsilon r\varsigma }{2}\sqrt{{{\vartheta }_{1}}} \right) \right) }^{2}}}, \end{aligned}$$
(4)

where \({{\vartheta }_{1}},{{\vartheta }_{2}},{{\vartheta }_{3}},r\) are real constants, and the functions\(F(\varsigma )\) satisfies the following equation:

$$\begin{aligned} {{\left( \frac{dF(\varsigma )}{d\varsigma } \right) }^{2}}-{{r}^{2}}{{F}^{2}}(\varsigma )\left( {{\vartheta }_{1}}\mp {{\vartheta }_{2}}F(\varsigma )\mp {{\vartheta }_{3}}F{{(\varsigma )}^{2}} \right) =0. \end{aligned}$$
(5)

Based on our existing approach, the resolution to the suggested model is depicted through the subsequent series employing foundational functions (3) and (4):

$$\begin{aligned} V(\varsigma )=\sum \nolimits _{i=0}^{N}{{{c}_{i}}}{{\left( F(\varsigma ) \right) }^{i}},{{c}_{N}}\ne 0, \end{aligned}$$
(6)

where \({{c}_{0}},{{c}_{1}},{{c}_{2}},...\) are the constants and N is the balancing value.

Application to the model

The present Kudryashov technique is used to the proposed conformable NLSE to derive a class of novel optical solutions in this section. Thus, we consider with the following transformations:

$$\begin{aligned} \begin{aligned}&q(x,t)=U(\varsigma ){{e}^{i\theta (x,t)}}, \\&\varsigma =\eta \left( x-\nu \frac{{{t}^{\alpha }}}{\alpha } \right) ,\theta (x,t)=u-kx+w\frac{{{t}^{\alpha }}}{\alpha }, \\ \end{aligned} \end{aligned}$$
(7)

where u is the phase center, k is the frequency of the soliton, and w is the wave of the frequency. The transformations in equation (7) are inserted into equation (1), we obtain the following:

$$\begin{aligned} \begin{aligned}&a{{\eta }^{2}}{U}''-U(a{{k}^{2}}+w)+{{b}_{1}}{{U}^{1-4n}}+{{b}_{2}}{{U}^{1-3n}}+{{b}_{3}}{{U}^{1-2n}}\\&\quad +{{b}_{4}}{{U}^{n-1}}+{{b}_{5}}{{U}^{n+1}}+{{b}_{6}}{{U}^{2n+1}}+{{b}_{7}}{{U}^{3n+1}}\\&\quad +{{b}_{8}}{{U}^{4n+1}} -k(\lambda +\mu ){{U}^{2m+1}}=0, \\ \end{aligned} \end{aligned}$$
(8)

and the imaginary part

$$\begin{aligned} \eta (\lambda +\mu +2m(\lambda +\theta )){{U}^{2m+1}}{U}'-\eta (2ak+v){U}'=0. \end{aligned}$$
(9)

From equation (9), we obtain

$$\begin{aligned} -(2ak+v)+(\lambda +\mu +2m(\lambda +\theta )){{U}^{2m+1}}=0. \end{aligned}$$
(10)

From the above equation, we obtain the following:

$$\begin{aligned}{} & {} \nu =-2ak, \end{aligned}$$
(11)
$$\begin{aligned}{} & {} \lambda +\mu +2m(\lambda +\theta )=0. \end{aligned}$$
(12)

Here, we insert the transformation \(U={{V}^{\frac{1}{2n}}}\) into equation (8), we obtain

$$\begin{aligned} \begin{aligned}&(2nV{V}''+{{{{V}'}}^{2}}(1-2n))a{{\eta }^{2}}-a{{n}^{2}}(a{{k}^{2}}+w){{V}^{2}}+4{{b}_{6}}{{n}^{2}}{{V}^{3}}\\&\quad +4{{b}_{1}}{{n}^{2}}+4{{b}_{2}}{{n}^{2}}{{V}^{\frac{1}{2}}}+4{{b}_{3}}{{n}^{2}}V+4{{b}_{4}}{{n}^{2}}{{V}^{\frac{3}{2}}} \\&\quad +4{{b}_{5}}{{n}^{2}}{{V}^{\frac{5}{2}}}+4{{b}_{7}}{{n}^{2}}{{B}^{\frac{7}{2}}}+4{{b}_{8}}{{n}^{2}}{{V}^{4}}\\&\quad -4k{{n}^{2}}(\mu +\lambda ){{V}^{\frac{m}{n}+2}}=0, \\ \end{aligned} \end{aligned}$$
(13)

In order to ensure the integrability of the aforementioned ordinary differential equation, it is necessary to assign values such that \(b_2 = b_4 = b_5 = b_7 = 0\) and \(m=2n\). Consequently, equation (13) is simplified to the subsequent expression:

$$\begin{aligned} \begin{aligned}&(2nV{V}''+{{{{V}'}}^{2}}(1-2n))a{{\eta }^{2}}+4{{b}_{6}}{{n}^{2}}{{V}^{3}}+4{{b}_{8}}{{n}^{2}}{{V}^{4}}\\&\quad -a{{n}^{2}}(a{{k}^{2}}+w){{V}^{2}}-4k{{n}^{2}}(\mu +\lambda ){{V}^{4}}+4{{b}_{3}}{{n}^{2}}V \\&\quad +4{{b}_{1}}{{n}^{2}}=0, \\ \end{aligned} \end{aligned}$$
(14)

Balancing the terms involving \({{{V}'}^{2}}\) and \({{V}^{4}}\) in the equation above, we obtain \(N=1\). Therefore, equation (6) becomes:

$$\begin{aligned} V(\varsigma )={{c}_{0}}+{{c}_{1}}F(\varsigma ),\,{{c}_{1}}\ne 0. \end{aligned}$$
(15)

Inserting the equation (15) with (5) into (14) and setting the coefficients of \({{F}^{i}}(\varsigma )(i=0,1,...)\) to zero, the following system is obtained:

$$\begin{aligned}{} & {} {{\left( F(\varsigma ) \right) }^{0}}\,:\,-4a{{k}^{2}}{{n}^{2}}c_{0}^{2}-4{{n}^{2}}wb_{0}^{2}-4k{{n}^{2}}\lambda c_{0}^{4}-4k{{n}^{2}}\mu c_{0}^{4}+4{{n}^{2}}{{b}_{1}}\\{} & {} \quad +4{{n}^{2}}{{c}_{0}}{{b}_{3}}+4{{n}^{2}}c_{0}^{3}{{b}_{6}}+4{{n}^{2}}c_{0}^{4}{{b}_{8}}=0,\\{} & {} {{\left( F(\varsigma ) \right) }^{1}}:\,-8a{{k}^{2}}{{n}^{2}}{{c}_{0}}{{c}_{1}}-8{{n}^{2}}w{{c}_{0}}{{c}_{1}}-16k{{n}^{2}}\lambda c_{0}^{3}{{c}_{1}}\\{} & {} \quad -16k{{n}^{2}}\mu c_{0}^{3}{{c}_{1}}+4{{n}^{2}}{{c}_{1}}{{b}_{3}}+12{{n}^{2}}c_{0}^{2}{{c}_{1}}{{b}_{6}}+16{{n}^{2}}c_{0}^{3}{{c}_{1}}{{b}_{8}}\\{} & {} \quad +2an{{r}^{2}}{{\eta }^{2}}{{c}_{0}}{{c}_{1}}{{\vartheta }_{1}}=0; \\{} & {} {{\left( F(\varsigma ) \right) }^{2}}:12{{n}^{2}}{{c}_{0}}c_{1}^{2}{{b}_{6}}-4a{{k}^{2}}{{n}^{2}}c_{1}^{2}-4{{n}^{2}}wb_{1}^{2}\\{} & {} \quad -24k{{n}^{2}}\lambda c_{0}^{2}c_{1}^{2}-24k{{n}^{2}}\mu c_{0}^{2}c_{1}^{2}+24{{n}^{2}}c_{0}^{2}c_{1}^{2}{{b}_{8}}+a{{r}^{2}}{{\eta }^{2}}c_{1}^{2}{{\vartheta }_{1}} \\{} & {} \quad +3an{{r}^{2}}{{\eta }^{2}}{{c}_{0}}{{c}_{1}}{{\vartheta }_{2}}=0, \\{} & {} {{\left( F(\varsigma ) \right) }^{3}}:\,-16k{{n}^{2}}\lambda {{c}_{0}}c_{1}^{3}-16k{{n}^{2}}\mu {{c}_{0}}c_{1}^{3}\\{} & {} \quad +16{{n}^{2}}{{c}_{0}}c_{1}^{3}{{b}_{8}}+a{{r}^{2}}{{\eta }^{2}}c_{1}^{2}{{\vartheta }_{2}}+an{{r}^{2}}{{\eta }^{2}}c_{1}^{2}{{\vartheta }_{2}}+4an{{r}^{2}}{{\eta }^{2}}{{c}_{0}}{{c}_{1}}{{\vartheta }_{3}} \\{} & {} \quad +4{{n}^{2}}c_{1}^{3}{{b}_{6}}=0, \\{} & {} {{\left( F(\varsigma ) \right) }^{4}}:\,-4k{{n}^{2}}\lambda c_{1}^{4}-4k{{n}^{2}}\mu c_{1}^{4}+4{{n}^{2}}c_{1}^{4}{{b}_{8}}\\{} & {} \quad +a{{r}^{2}}{{\eta }^{2}}c_{1}^{2}{{\vartheta }_{3}}+2an{{r}^{2}}{{\eta }^{2}}c_{1}^{2}{{\vartheta }_{3}}=0. \end{aligned}$$

The above system leads to the following solutions:


Result-1:

$$\begin{aligned} \begin{aligned}&{{b}_{1}}=\frac{\left( -1+2n \right) c_{0}^{2}\left( k\left( \lambda +\mu \right) -{{b}_{8}} \right) \left( c_{1}^{2}{{\vartheta }_{1}}-{{c}_{0}}{{c}_{1}}{{\vartheta }_{2}}+c_{0}^{2}{{\vartheta }_{3}} \right) }{\left( 1+2n \right) {{\vartheta }_{3}}},\\&\quad {{b}_{6}}=\frac{\left( 1+n \right) \left( k\left( \lambda +\mu \right) -{{b}_{8}} \right) \left( -{{c}_{1}}{{\vartheta }_{2}}+4{{c}_{0}}{{\vartheta }_{3}} \right) }{\left( 1+2n \right) {{\vartheta }_{3}}}, \\&w=-\frac{\left( k\left( \lambda +\mu \right) -{{b}_{8}} \right) \left( c_{1}^{2}\left( 4{{k}^{2}}{{n}^{2}}-{{r}^{2}}{{\eta }^{2}}{{\vartheta }_{1}} \right) +3{{r}^{2}}{{\eta }^{2}}{{c}_{0}}{{c}_{1}}{{\vartheta }_{2}}-6{{r}^{2}}{{\eta }^{2}}c_{0}^{2}{{\vartheta }_{3}} \right) }{\left( 1+2n \right) {{r}^{2}}{{\eta }^{2}}{{\vartheta }_{3}}}, \\&a=\frac{4{{n}^{2}}c_{1}^{2}\left( k\left( \lambda +\mu \right) -{{b}_{8}} \right) }{\left( 1+2n \right) {{r}^{2}}{{\eta }^{2}}{{\vartheta }_{3}}};\\&\quad {{b}_{3}}=-\frac{\left( -1+n \right) {{c}_{0}}\left( k\left( \lambda +\mu \right) -{{b}_{8}} \right) \left( 2c_{1}^{2}{{\vartheta }_{1}}-3{{c}_{0}}{{c}_{1}}{{\vartheta }_{2}}+4c_{0}^{2}{{\vartheta }_{3}} \right) }{\left( 1+2n \right) {{\vartheta }_{3}}}. \\ \end{aligned} \end{aligned}$$
(16)

Using (3), (7), (11), (12), (15), and (16), the following exponential solutions to the present model are acquired:

$$\begin{aligned}{} & {} {{q}_{1}}(x,t)={{\text {e}}^{\text {i}\left( u-kx-w\frac{{{t}^{\alpha }}}{\alpha } \right) }}\nonumber \\{} & {} \quad {{\left[ {{c}_{0}}+\frac{4{{c}_{1}}{{\vartheta }_{1}}}{{{\text {e}}^{-r\eta \sqrt{{{\vartheta }_{1}}}\left( x+{{L}_{1}} \right) }}-2{{\vartheta }_{2}}+{{\text {e}}^{r\eta \sqrt{{{\vartheta }_{1}}}\left( x+{{L}_{1}} \right) }}\left( \vartheta _{2}^{2}-4{{\vartheta }_{1}}{{\vartheta }_{3}} \right) } \right] }^{\frac{1}{2n}}}, \end{aligned}$$
(17)

where \({{L}_{1}}=\frac{8k{{n}^{2}}{{t}^{\alpha }}c_{1}^{2}\left( k\left( \lambda +\mu \right) -{{b}_{8}} \right) }{\left( 1+2n \right) {{r}^{2}}\alpha {{\eta }^{2}}{{\vartheta }_{3}}}.\)

Using (4), (7), (11), (12), (15), and (16), the following hyperbolic solutions to the present model are acquired:

$$\begin{aligned}{} & {} {{q}_{2}}(x,t)={{\text {e}}^{\text {i}\left( u-kx-w\frac{{{t}^{\alpha }}}{\alpha } \right) }}\nonumber \\{} & {} \quad {{\left[ {{c}_{0}}-\frac{{\text {sech}}{{\left[ \frac{1}{2}r\eta \sqrt{{{\vartheta }_{1}}}\left( x+\frac{8k{{n}^{2}}c_{1}^{2}\left( k\left( \lambda +\mu \right) -{{b}_{8}} \right) {{t}^{\alpha }}}{\left( 1+2n \right) {{r}^{2}}{{\eta }^{2}}{{\vartheta }_{3}}\alpha } \right) \right] }^{2}}{{c}_{1}}{{\vartheta }_{1}}{{\vartheta }_{2}}}{\vartheta _{2}^{2}-{{\vartheta }_{1}}{{\vartheta }_{3}}{{\left( 1-\tanh \left[ \frac{1}{2}r\eta \sqrt{{{\vartheta }_{1}}}\left( x+\frac{8k{{n}^{2}}c_{1}^{2}\left( k\left( \lambda +\mu \right) -{{b}_{8}} \right) {{t}^{\alpha }}}{\left( 1+2n \right) {{r}^{2}}{{\eta }^{2}}{{\vartheta }_{3}}\alpha } \right) \right] \right) }^{2}}} \right] }^{\frac{1}{2n}}}. \end{aligned}$$
(18)
Fig. 1
figure 1

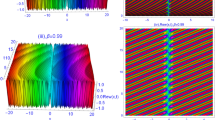
The comparison of wave solutions for \({\text {Re}}({{q}_{1}}(x,t))\) and \({\text {Im}}({{q}_{1}}(x,t))\)for \(\alpha =1\) and \(\alpha =0.3\), where \({{\left| {{q}_{1}}(x,t) \right| }^{2}}\), where \(a=-0.9,r=0.9,n=3,{{b}_{8}}=\mu =k=1,{{\vartheta }_{1}}=0.4,{{\vartheta }_{2}}=-0.2,{{\vartheta }_{3}}=-0.9,{{c}_{0}}=1,u={{c}_{1}}=0.7,{b }_{1}=0.6,\eta =-1,\lambda =0.2,\) and \(\alpha =1\)

Full size image
Fig. 2
figure 2

The bell-shaped solutions of \({{\left| {{q}_{1}}(x,t) \right| }^{2}}\), where \(a=-0.9,r=0.9,n=3,{{b}_{8}}=\mu =k=1,{{\vartheta }_{1}}=0.4,{{\vartheta }_{2}}=-0.2,{{\vartheta }_{3}}=-0.9,{{c}_{0}}=1,u={{c}_{1}}=0.7,{b }_{1}=0.6,\eta =-1,\lambda =0.2,\) and \(\alpha =1\)

Full size image
Fig. 3
figure 3

The comparison of bright solutions \({{\left| {{q}_{3}}(x,t) \right| }^{2}}\) for \(\alpha =1\) and \(\alpha =0.3\), where \(a=-0.9,r=0.9,n=3,{{b}_{1}}=0.6,\mu =k=1,{{\vartheta }_{2}}=-0.2,{{\vartheta }_{3}}=-0.9,{{c}_{0}}=1,u={{c}_{1}}=0.7,{b }_{1}=0.6,\eta =-1,\lambda =0.2,\) and \(\lambda =0.2\)

Full size image
Fig. 4
figure 4

The comparison of mixed dark-bright solutions of \({{\left| {{q}_{7}}(x,t) \right| }^{2}}\), where \(a=-0.9,r=0.9,n=3,{{b}_{8}}=\mu =k=1,,{{\vartheta }_{1}}=0.4,{{b}_{6}}={{\vartheta }_{2}}=0.2,{{c}_{0}}=1,u={{c}_{1}}=0.7,{b }_{1}=0.6,\eta =-1,\) and \(\lambda =0.2\)

Full size image
Fig. 5
figure 5

The comparison of multi-dark solutions of \({{\left| {{q}_{9}}(x,t) \right| }^{2}}\), where \(a=-0.9,r=0.9,n=3,{{b}_{8}}=\mu =k=1,,{{\vartheta }_{1}}=0.4,{{b}_{6}}={{\vartheta }_{2}}=0.2,{{c}_{0}}=1,u={{c}_{1}}=0.7,{b }_{1}=0.6,\eta =-1,\) and \(\lambda =0.2\)

Full size image

Result-2:

$$\begin{aligned} \begin{aligned}&w=\frac{{{b}_{1}}}{\left( -1+2n \right) c_{0}^{2}}-a{{k}^{2}}-\frac{a{{r}^{2}}{{\eta }^{2}}{{c}_{0}}{{\vartheta }_{2}}}{2{{n}^{2}}{{c}_{1}}}+\frac{5a{{r}^{2}}{{\eta }^{2}}c_{0}^{2}{{\vartheta }_{3}}}{4{{n}^{2}}c_{1}^{2}},\\&\quad {{\vartheta }_{1}}=\frac{4{{n}^{2}}{{b}_{1}}}{a\left( 2n-1 \right) {{r}^{2}}{{\eta }^{2}}c_{0}^{2}}+\frac{{{c}_{0}}{{\vartheta }_{2}}}{{{c}_{1}}}-\frac{c_{0}^{2}{{\vartheta }_{3}}}{c_{1}^{2}}, \\&{{b}_{3}}=-\frac{\left( -1+n \right) \left( 8{{n}^{2}}c_{1}^{2}{{b}_{1}}+a\left( 1-2n \right) {{r}^{2}}{{\eta }^{2}}c_{0}^{3}{{c}_{1}}{{\vartheta }_{2}}+2a\left( -1+2n \right) {{r}^{2}}{{\eta }^{2}}c_{0}^{4}{{\vartheta }_{3}} \right) }{4{{n}^{2}}\left( -1+2n \right) {{c}_{0}}c_{1}^{2}}, \\&\mu =\frac{-4k\lambda +4{{b}_{8}}+\frac{a\left( 1+2n \right) {{r}^{2}}{{\eta }^{2}}{{\vartheta }_{3}}}{{{n}^{2}}c_{1}^{2}}}{4k},\\&\quad {{b}_{6}}=-\frac{a\left( 1+n \right) {{r}^{2}}{{\eta }^{2}}\left( {{c}_{1}}{{\vartheta }_{2}}-4{{c}_{0}}{{\vartheta }_{3}} \right) }{4{{n}^{2}}c_{1}^{2}}. \\ \end{aligned} \end{aligned}$$
(19)

Using (3), (7), (11), (12), (15), and (19), the following exponential solutions to the present model are acquired:

Fig. 6
figure 6

The wave solutions of \({\text {Im}}({{q}_{10}}(x,t))\), where \(a=-0.9,r=0.9,n=3,{{b}_{8}}=\mu =k=1,,{{\vartheta }_{1}}=0.4,{{b}_{6}}={{\vartheta }_{2}}=0.2,{{c}_{0}}=1,u={{c}_{1}}=0.7,{b }_{1}=0.6,\eta =-1,\lambda =0.2,\) and \(\alpha =1\)

Full size image
Fig. 7
figure 7

The dark solutions of \({{\left| {{q}_{10}}(x,t) \right| }^{2}}\), where \(a=-0.9,r=0.9,n=3,{{b}_{8}}=\mu =k=1,,{{\vartheta }_{1}}=0.4,{{b}_{6}}={{\vartheta }_{2}}=0.2,{{c}_{0}}=1,u={{c}_{1}}=0.7,{b }_{1}=0.6,\eta =-1,\lambda =0.2,\) and \(\alpha =1\)

Full size image
Fig. 8
figure 8

The effect of \(\alpha\) on the optical solutions \({{\left| {{q}_{7}}(x,2.5) \right| }^{2}}\) and \({\text {Re}}({{q}_{7}}(x,2))\) where \(a=-0.9,r=0.9,n=3,{{b}_{8}}=\mu =k=1,,{{\vartheta }_{1}}=0.4,{{b}_{6}}={{\vartheta }_{2}}=0.2,{{c}_{0}}=1,u={{c}_{1}}=0.7,{b }_{1}=0.6,\eta =-1,\) and \(\lambda =0.2\)

Full size image
Fig. 9
figure 9

The effect of \(\alpha\) on the optical solutions \({{\left| {{q}_{9}}(x,2) \right| }^{2}}\) and \({\text {Im}}({{q}_{9}}(x,2))\), where \(a=-0.9,r=0.9,n=3,{{b}_{8}}=\mu =k=1,,{{\vartheta }_{1}}=0.4,{{b}_{6}}={{\vartheta }_{2}}=0.2,{{c}_{0}}=1,u={{c}_{1}}=0.7,{b }_{1}=0.6,\eta =-1,\) and \(\lambda =0.2\)

Full size image
$$\begin{aligned}{} & {} {{q}_{3}}(x,t)={{\text {e}}^{\text {i}\left( u-kx+\frac{{{t}^{\alpha }}\left( \frac{{{b}_{1}}}{\left( 2n-1 \right) c_{0}^{2}}-a{{k}^{2}}-\frac{a{{r}^{2}}{{\eta }^{2}}{{c}_{0}}{{\vartheta }_{2}}}{2{{n}^{2}}{{c}_{1}}}+\frac{5a{{r}^{2}}{{\eta }^{2}}c_{0}^{2}{{\vartheta }_{3}}}{4{{n}^{2}}c_{1}^{2}} \right) }{\alpha } \right) }}\nonumber \\{} & {} \quad {{\left[ {{c}_{0}}+\frac{4{{c}_{1}}\left( \frac{4{{n}^{2}}{{b}_{1}}}{a\left( 2n-1 \right) {{r}^{2}}{{\eta }^{2}}c_{0}^{2}}+\frac{{{c}_{0}}{{\vartheta }_{2}}}{{{c}_{1}}}-\frac{c_{0}^{2}{{\vartheta }_{3}}}{c_{1}^{2}} \right) }{{{\text {e}}^{-r\left( x+\frac{2ak{{t}^{\alpha }}}{\alpha } \right) \eta {{L}_{2}}}}-2{{\vartheta }_{2}}+{{\text {e}}^{r\left( x+\frac{2ak{{t}^{\alpha }}}{\alpha } \right) \eta {{L}_{2}}}}{{B}_{1}}} \right] }^{\frac{1}{2n}}}, \end{aligned}$$
(20)

where \({{L}_{2}}=\sqrt{\frac{4{{n}^{2}}{{b}_{1}}}{a\left( -1+2n \right) {{r}^{2}}{{\eta }^{2}}c_{0}^{2}}+\frac{{{c}_{0}}{{\vartheta }_{2}}}{{{c}_{1}}}-\frac{c_{0}^{2}{{\vartheta }_{3}}}{c_{1}^{2}}}\) and \({{B}_{1}}=\vartheta _{2}^{2}-4{{\vartheta }_{3}}\left( \frac{4{{n}^{2}}{{b}_{1}}}{a\left( -1+2n \right) {{r}^{2}}{{\eta }^{2}}c_{0}^{2}}+\frac{{{c}_{0}}{{\vartheta }_{2}}}{{{c}_{1}}}-\frac{c_{0}^{2}{{\vartheta }_{3}}}{c_{1}^{2}} \right)\).

Using (4), (7), (11), (12), (15), and (19), the following hyperbolic solutions to the present model are acquired:

$$\begin{aligned}{} & {} {{q}_{4}}(x,t)={{\text {e}}^{\text {i}\left( u-kx+w\frac{{{t}^{\alpha }}}{\alpha } \right) }}\nonumber \\{} & {} \quad {{\left[ \frac{{\text {sech}}{{\left[ \frac{1}{2}r\eta {{L}_{2}}\varsigma \right] }^{2}}{{c}_{1}}{{\vartheta }_{2}}\left( \frac{c_{0}^{2}{{\vartheta }_{3}}}{c_{1}^{2}}-\frac{4{{n}^{2}}{{b}_{1}}}{a\left( 2n-1 \right) {{r}^{2}}{{\eta }^{2}}c_{0}^{2}}-\frac{{{c}_{0}}{{\vartheta }_{2}}}{{{c}_{1}}} \right) }{\vartheta _{2}^{2}-{{\vartheta }_{3}}\left( \frac{4{{n}^{2}}{{b}_{1}}}{a\left( 2n-1 \right) {{r}^{2}}{{\eta }^{2}}c_{0}^{2}}+\frac{{{c}_{0}}{{\vartheta }_{2}}}{{{c}_{1}}}-\frac{c_{0}^{2}{{\vartheta }_{3}}}{c_{1}^{2}} \right) {{\left( 1-\tanh \left[ \frac{1}{2}r\eta {{L}_{2}}\varsigma \right] \right) }^{2}}} \right] }^{\frac{1}{2n}}}, \end{aligned}$$
(21)

where \(\varsigma =x+\frac{2ak{{t}^{\alpha }}}{\alpha }.\)


Result-3:

$$\begin{aligned} \begin{aligned}&{{b}_{3}}=\frac{\left( -1+n \right) {{b}_{1}}\left( 2{{c}_{1}}{{\vartheta }_{1}}-3{{c}_{0}}{{\vartheta }_{2}} \right) }{\left( -1+2n \right) {{c}_{0}}\left( -{{c}_{1}}{{\vartheta }_{1}}+{{c}_{0}}{{\vartheta }_{2}} \right) },\\&w=\frac{{{b}_{1}}\left( {{c}_{1}}\left( 4{{k}^{2}}{{n}^{2}}-{{r}^{2}}{{\eta }^{2}}{{\vartheta }_{1}} \right) +3{{r}^{2}}{{\eta }^{2}}{{c}_{0}}{{\vartheta }_{2}} \right) }{\left( -1+2n \right) {{r}^{2}}{{\eta }^{2}}c_{0}^{2}\left( -{{c}_{1}}{{\vartheta }_{1}}+{{c}_{0}}{{\vartheta }_{2}} \right) },\\&\mu =-\lambda +\frac{{{b}_{8}}}{k}, \\&{{\vartheta }_{3}}=0,{{b}_{6}}=\frac{\left( 1+n \right) {{b}_{1}}{{\vartheta }_{2}}}{\left( -1+2n \right) c_{0}^{2}\left( -{{c}_{1}}{{\vartheta }_{1}}+{{c}_{0}}{{\vartheta }_{2}} \right) },\\&a=\frac{4{{n}^{2}}{{c}_{1}}{{b}_{1}}}{\left( -1+2n \right) {{r}^{2}}{{\eta }^{2}}c_{0}^{2}\left( {{c}_{1}}{{\vartheta }_{1}}-{{c}_{0}}{{\vartheta }_{2}} \right) }. \\ \end{aligned} \end{aligned}$$
(22)

Using (3), (7), (11), (12), (15), and (22), the following exponential solutions to the present model are acquired:

$$\begin{aligned}{} & {} {{q}_{5}}(x,t)={{\text {e}}^{\text {i}\left( u-kx+\frac{{{t}^{\alpha }}{{b}_{1}}\left( {{c}_{1}}\left( 4{{k}^{2}}{{n}^{2}}-{{r}^{2}}{{\eta }^{2}}{{\vartheta }_{1}} \right) +3{{r}^{2}}{{\eta }^{2}}{{c}_{0}}{{\vartheta }_{2}} \right) }{\left( -1+2n \right) {{r}^{2}}\alpha {{\eta }^{2}}c_{0}^{2}\left( -{{c}_{1}}{{\vartheta }_{1}}+{{c}_{0}}{{\vartheta }_{2}} \right) } \right) }}\nonumber \\{} & {} \quad {{\left[ {{c}_{0}}+\frac{4{{c}_{1}}{{\vartheta }_{1}}}{{{\text {e}}^{-r\eta \sqrt{{{\vartheta }_{1}}}\left( x+{{L}_{3}} \right) }}-2{{\vartheta }_{2}}+{{\text {e}}^{r\eta \sqrt{{{\vartheta }_{1}}}\left( x+{{L}_{3}} \right) }}\vartheta _{2}^{2}} \right] }^{\frac{1}{2n}}}, \end{aligned}$$
(23)

where \({{L}_{3}}=\frac{8k{{n}^{2}}{{t}^{\alpha }}{{c}_{1}}{{b}_{1}}}{\left( -1+2n \right) {{r}^{2}}\alpha {{\eta }^{2}}c_{0}^{2}\left( {{c}_{1}}{{\vartheta }_{1}}-{{c}_{0}}{{\vartheta }_{2}} \right) }\).

Using (4), (7), (11), (12), (15), and (22), the following hyperbolic solutions to the present model are acquired:

$$\begin{aligned}{} & {} {{q}_{6}}(x,t)={{\text {e}}^{\text {i}\left( u-kx+\frac{{{t}^{\alpha }}{{b}_{1}}\left( {{c}_{1}}\left( 4{{k}^{2}}{{n}^{2}}-{{r}^{2}}{{\eta }^{2}}{{\vartheta }_{1}} \right) +3{{r}^{2}}{{\eta }^{2}}{{c}_{0}}{{\vartheta }_{2}} \right) }{\left( -1+2n \right) {{r}^{2}}\alpha {{\eta }^{2}}c_{0}^{2}\left( -{{c}_{1}}{{\vartheta }_{1}}+{{c}_{0}}{{\vartheta }_{2}} \right) } \right) }}\nonumber \\{} & {} \quad {{\left[ {{c}_{0}}-\frac{{\text {sech}}{{\left[ \frac{1}{2}r\eta \sqrt{{{\vartheta }_{1}}}\left( x+{{L}_{3}} \right) \right] }^{2}}{{c}_{1}}{{\vartheta }_{1}}}{{{\vartheta }_{2}}} \right] }^{\frac{1}{2n}}}. \end{aligned}$$
(24)

Result-4:

$$\begin{aligned} \begin{aligned}&{{b}_{3}}=\frac{\left( -1+n \right) {{c}_{0}}\left( 2{{n}^{2}}{{c}_{0}}\left( -3\left( 1+2n \right) {{b}_{6}}+8\left( 1+n \right) {{c}_{0}}\left( k\left( \lambda +\mu \right) -{{b}_{8}} \right) \right) -a\left( 1+n \right) \left( 1+2n \right) {{r}^{2}}{{\eta }^{2}}{{\vartheta }_{1}} \right) }{2{{n}^{2}}\left( 1+n \right) \left( 1+2n \right) }, \\&{{b}_{1}}=\frac{\left( -1+2n \right) c_{0}^{2}\left( 4{{n}^{2}}{{c}_{0}}\left( \left( 1+2n \right) {{b}_{6}}-3\left( 1+n \right) {{c}_{0}}\left( k\left( \lambda +\mu \right) -{{b}_{8}} \right) \right) +a\left( 1+n \right) \left( 1+2n \right) {{r}^{2}}{{\eta }^{2}}{{\vartheta }_{1}} \right) }{4{{n}^{2}}\left( 1+n \right) \left( 1+2n \right) }, \\&w=-a{{k}^{2}}+\frac{3{{c}_{0}}{{b}_{6}}}{1+n}-\frac{6c_{0}^{2}\left( k\left( \lambda +\mu \right) -{{b}_{8}} \right) }{1+2n}+\frac{a{{r}^{2}}{{\eta }^{2}}{{\vartheta }_{1}}}{4{{n}^{2}}}, \\&{{c}_{1}}=\frac{a\left( 1+n \right) \left( 1+2n \right) {{r}^{2}}{{\eta }^{2}}{{\vartheta }_{2}}}{4{{n}^{2}}\left( -\left( \left( 1+2n \right) {{b}_{6}} \right) +4\left( 1+n \right) {{c}_{0}}\left( k\left( \lambda +\mu \right) -{{b}_{8}} \right) \right) }, \\&{{\vartheta }_{3}}=\frac{a{{\left( 1+n \right) }^{2}}\left( 1+2n \right) {{r}^{2}}{{\eta }^{2}}\left( k\left( \lambda +\mu \right) -{{b}_{8}} \right) \vartheta _{2}^{2}}{4{{n}^{2}}{{\left( \left( 1+2n \right) {{b}_{6}}-4\left( 1+n \right) {{c}_{0}}\left( k\left( \lambda +\mu \right) -{{b}_{8}} \right) \right) }^{2}}}. \\ \end{aligned} \end{aligned}$$
(25)

Using (3), (7), (11), (12), (15), and (25), the following exponential solutions to the present model are acquired:

$$\begin{aligned}{} & {} {{q}_{7}}(x,t)={{\text {e}}^{\text {i}\left( u-kx+w\frac{{{t}^{\alpha }}}{\alpha } \right) }}\nonumber \\{} & {} \quad {{\left[ {{c}_{0}}+\frac{a\left( 1+n \right) \left( 1+2n \right) {{r}^{2}}{{\eta }^{2}}{{\vartheta }_{1}}{{\vartheta }_{2}}}{{{n}^{2}}\left( {{B}_{2}} \right) \left( {{\text {e}}^{-r\left( x+\frac{2ak{{t}^{\alpha }}}{\alpha } \right) \eta \sqrt{{{\vartheta }_{1}}}}}-2{{\vartheta }_{2}}+{{\text {e}}^{r\left( x+\frac{2ak{{t}^{\alpha }}}{\alpha } \right) \eta \sqrt{{{\vartheta }_{1}}}}}\left( \vartheta _{2}^{2}-{{L}_{4}} \right) \right) } \right] }^{\frac{1}{2n}}}, \end{aligned}$$
(26)

where \({{L}_{4}}=\frac{a{{\left( 1+n \right) }^{2}}\left( 1+2n \right) {{r}^{2}}{{\eta }^{2}}\left( k\left( \lambda +\mu \right) -{{b}_{8}} \right) {{\vartheta }_{1}}\vartheta _{2}^{2}}{{{n}^{2}}{{\left( \left( 1+2n \right) {{b}_{6}}-4\left( 1+n \right) {{c}_{0}}\left( k\left( \lambda +\mu \right) -{{b}_{8}} \right) \right) }^{2}}}\) and \({{B}_{2}}=-\left( \left( 1+2n \right) {{b}_{6}} \right) +4\left( 1+n \right) {{c}_{0}}\left( k\left( \lambda +\mu \right) -{{b}_{8}} \right) .\)

Using (4), (7), (11), (12), (15), and (25), the following hyperbolic solutions to the present model are acquired:

$$\begin{aligned}{} & {} {{q}_{8}}(x,t)={{\text {e}}^{\text {i}\left( u-kx+w\frac{{{t}^{\alpha }}}{\alpha } \right) }}\nonumber \\{} & {} \quad {{\left[ \frac{a\left( 1+n \right) \left( 1+2n \right) {{r}^{2}}{{\eta }^{2}}{\text {sech}}{{\left[ \frac{1}{2}r\left( x+\frac{2ak{{t}^{\alpha }}}{\alpha } \right) \eta \sqrt{{{\vartheta }_{1}}} \right] }^{2}}{{\vartheta }_{1}}\vartheta _{2}^{2}}{4{{n}^{2}}\left( {{B}_{2}} \right) \left( \vartheta _{2}^{2}-\frac{{{A}_{1}}{{\left( 1-\tanh \left[ \frac{1}{2}r\left( x+\frac{2ak{{t}^{\alpha }}}{\alpha } \right) \eta \sqrt{{{\vartheta }_{1}}} \right] \right) }^{2}}}{4{{n}^{2}}{{\left( \left( 1+2n \right) {{b}_{6}}-4\left( 1+n \right) {{c}_{0}}\left( k\left( \lambda +\mu \right) -{{b}_{8}} \right) \right) }^{2}}} \right) } \right] }^{\frac{1}{2n}}}. \end{aligned}$$
(27)

where \({{A}_{1}}=a{{\left( 1+n \right) }^{2}}\left( 1+2n \right) {{r}^{2}}{{\eta }^{2}}\left( k\left( \lambda +\mu \right) -{{b}_{8}} \right) {{\vartheta }_{1}}\vartheta _{2}^{2}\).


Result-5:

$$\begin{aligned} \begin{aligned}&{{c}_{1}}=\pm \frac{\sqrt{-a{{\vartheta }_{3}}\left( 1+2n \right) }r\eta }{2\sqrt{{{n}^{2}}\left( -k\left( \lambda +\mu \right) +{{b}_{8}} \right) }},w=-a{{k}^{2}}+\frac{3{{b}_{1}}}{\left( -1+2n \right) c_{0}^{2}}+\frac{3c_{0}^{2}\left( k\left( \lambda +\mu \right) -{{b}_{8}} \right) }{1+2n}-\frac{a{{r}^{2}}{{\eta }^{2}}{{\vartheta }_{1}}}{2{{n}^{2}}}, \\&{{b}_{3}}=\frac{\left( -1+n \right) \left( 4{{n}^{2}}\left( -3\left( 1+2n \right) {{b}_{1}}-\left( -1+2n \right) c_{0}^{4}\left( k\left( \lambda +\mu \right) -{{b}_{8}} \right) \right) +a\left( -1+4{{n}^{2}} \right) {{r}^{2}}{{\eta }^{2}}c_{0}^{2}{{\vartheta }_{1}} \right) }{4{{n}^{2}}\left( -1+4{{n}^{2}} \right) {{c}_{0}}}, \\&{{b}_{6}}=\frac{\left( 1+n \right) \left( 4{{n}^{2}}\left( \left( 1+2n \right) {{b}_{1}}+3\left( -1+2n \right) c_{0}^{4}\left( k\left( \lambda +\mu \right) -{{b}_{8}} \right) \right) +a\left( 1-4{{n}^{2}} \right) {{r}^{2}}{{\eta }^{2}}c_{0}^{2}{{\vartheta }_{1}} \right) }{4{{n}^{2}}\left( -1+4{{n}^{2}} \right) c_{0}^{3}}, \\&{{\vartheta }_{2}}=\frac{\sqrt{1+2n}\left( 4{{n}^{2}}\left( -\left( \left( 1+2n \right) {{b}_{1}} \right) +\left( 2n-1 \right) c_{0}^{4}\left( k\left( \lambda +\mu \right) -{{b}_{8}} \right) \right) +a\left( 4{{n}^{2}}-1 \right) {{r}^{2}}{{\eta }^{2}}c_{0}^{2}{{\vartheta }_{1}} \right) \sqrt{-{{\vartheta }_{3}}}}{2\sqrt{a}\left( -1+4{{n}^{2}} \right) r\eta c_{0}^{3}\sqrt{{{n}^{2}}\left( -k\left( \lambda +\mu \right) +{{b}_{8}} \right) }}. \\ \end{aligned} \end{aligned}$$
(28)

Using (3), (7), (11), (12), (15), and (28), the following exponential solutions to the present model are acquired:

$$\begin{aligned}{} & {} {{q}_{9}}(x,t)={{\text {e}}^{\text {i}\left( u-kx+w\frac{{{t}^{\alpha }}}{\alpha } \right) }}\nonumber \\{} & {} \quad {{\left[ {{c}_{0}}+\frac{2r\eta {{\vartheta }_{1}}\sqrt{-a{{\vartheta }_{3}}\left( 1+2n \right) }}{\sqrt{{{n}^{2}}\left( {{b}_{8}}-k\left( \lambda +\mu \right) \right) }\left( {{\text {e}}^{-r\left( x+\frac{2ak{{t}^{\alpha }}}{\alpha } \right) \eta \sqrt{{{\vartheta }_{1}}}}}-{{B}_{3}}\text {-}{{\text {e}}^{r\left( x+\frac{2ak{{t}^{\alpha }}}{\alpha } \right) \eta \sqrt{{{\vartheta }_{1}}}}}\left( 4{{\vartheta }_{1}}{{\vartheta }_{3}}+{{L}_{5}} \right) \right) } \right] }^{\frac{1}{2n}}}. \end{aligned}$$
(29)

where \(\varsigma =x+\frac{2ak{{t}^{\alpha }}}{\alpha }\), \({{L}_{5}}=\frac{\left( 1+2n \right) {{\left( 4{{n}^{2}}\left( -\left( \left( 1+2n \right) {{b}_{1}} \right) +\left( 2n-1 \right) c_{0}^{4}\left( k\left( \lambda +\mu \right) -{{b}_{8}} \right) \right) +a\left( 4{{n}^{2}}-1 \right) {{r}^{2}}{{\eta }^{2}}c_{0}^{2}{{\vartheta }_{1}} \right) }^{2}}{{\vartheta }_{3}}}{4a{{n}^{2}}{{\left( -1+4{{n}^{2}} \right) }^{2}}{{r}^{2}}{{\eta }^{2}}c_{0}^{6}\left( -k\left( \lambda +\mu \right) +{{b}_{8}} \right) }\), and \({{B}_{3}}=\frac{\sqrt{-{{\vartheta }_{3}}\left( 1+2n \right) }\left( 4{{n}^{2}}\left( -\left( \left( 1+2n \right) {{b}_{1}} \right) +\left( 2n-1 \right) c_{0}^{4}\left( k\left( \lambda +\mu \right) -{{b}_{8}} \right) \right) +a\left( 4{{n}^{2}}-1 \right) {{r}^{2}}{{\eta }^{2}}c_{0}^{2}{{\vartheta }_{1}} \right) }{\sqrt{a}\left( -1+4{{n}^{2}} \right) r\eta c_{0}^{3}\sqrt{{{n}^{2}}\left( -k\left( \lambda +\mu \right) +{{b}_{8}} \right) }}\).

Using (4), (7), (11), (12), (15), and (28), the following hyperbolic solutions to the present model are acquired:

$$\begin{aligned}{} & {} {{q}_{10}}(x,t)={{\text {e}}^{\text {i}\left( u-kx+w\frac{{{t}^{\alpha }}}{\alpha } \right) }}\nonumber \\{} & {} \quad {{\left[ {{c}_{0}}+\frac{\left( 1+2n \right) {\text {sech}}{{\left[ \frac{1}{2}r\left( x+\frac{2ak{{t}^{\alpha }}}{\alpha } \right) \eta \sqrt{{{\vartheta }_{1}}} \right] }^{2}}{{B}_{4}}}{{{L}_{6}}\left( {{A}_{2}}-{{\vartheta }_{1}}{{\vartheta }_{3}}{{\left( 1-\tanh \left[ \frac{1}{2}r\left( x+\frac{2ak{{t}^{\alpha }}}{\alpha } \right) \eta \sqrt{{{\vartheta }_{1}}} \right] \right) }^{2}} \right) } \right] }^{\frac{1}{2n}}}. \end{aligned}$$
(30)

where \({{A}_{2}}=\frac{\left( 1+2n \right) {{\left( 4{{n}^{2}}\left( -\left( \left( 1+2n \right) {{b}_{1}} \right) +\left( 2n-1 \right) c_{0}^{4}\left( k\left( \lambda +\mu \right) -{{b}_{8}} \right) \right) +a\left( 4{{n}^{2}}-1 \right) {{r}^{2}}{{\eta }^{2}}c_{0}^{2}{{\vartheta }_{1}} \right) }^{2}}{{\vartheta }_{3}}}{-4a{{n}^{2}}{{\left( -1+4{{n}^{2}} \right) }^{2}}{{r}^{2}}{{\eta }^{2}}c_{0}^{6}\left( -k\left( \lambda +\mu \right) +{{b}_{8}} \right) }\), \({{B}_{4}}={{\vartheta }_{1}}\left( 4{{n}^{2}}\left( -\left( \left( 1+2n \right) {{b}_{1}} \right) +\left( 2n-1 \right) c_{0}^{4}\left( k\left( \lambda +\mu \right) -{{b}_{8}} \right) \right) +a\left( 4{{n}^{2}}-1 \right) {{r}^{2}}{{\eta }^{2}}c_{0}^{2}{{\vartheta }_{1}} \right) {{\vartheta }_{3}}\), and \({{L}_{6}}=4{{n}^{2}}\left( -1+4{{n}^{2}} \right) c_{0}^{3}\left( -k\left( \lambda +\mu \right) +{{b}_{8}} \right) .\)


Result-6:

$$\begin{aligned} \begin{aligned}&w=\frac{3a{{r}^{2}}{{\eta }^{2}}c_{0}^{2}{{\vartheta }_{3}}}{4{{n}^{2}}c_{1}^{2}}-a{{k}^{2}}+\frac{3{{b}_{1}}}{\left( -1+2n \right) c_{0}^{2}}-\frac{a{{r}^{2}}{{\eta }^{2}}{{\vartheta }_{1}}}{2{{n}^{2}}}, \\&{{b}_{3}}=-\frac{\left( -1+n \right) \left( c_{1}^{2}\left( 12{{n}^{2}}{{b}_{1}}+a\left( 1-2n \right) {{r}^{2}}{{\eta }^{2}}c_{0}^{2}{{\vartheta }_{1}} \right) +a\left( -1+2n \right) {{r}^{2}}{{\eta }^{2}}c_{0}^{4}{{\vartheta }_{3}} \right) }{4{{n}^{2}}\left( -1+2n \right) {{c}_{0}}c_{1}^{2}}, \\&{{b}_{6}}=\frac{\left( 1+n \right) \left( c_{1}^{2}\left( 4{{n}^{2}}{{b}_{1}}+a\left( 1-2n \right) {{r}^{2}}{{\eta }^{2}}c_{0}^{2}{{\vartheta }_{1}} \right) +3a\left( -1+2n \right) {{r}^{2}}{{\eta }^{2}}c_{0}^{4}{{\vartheta }_{3}} \right) }{4{{n}^{2}}\left( -1+2n \right) c_{0}^{3}c_{1}^{2}}, \\&{{\vartheta }_{2}}=\frac{{{c}_{1}}{{\vartheta }_{1}}}{{{c}_{0}}}+\frac{{{c}_{0}}{{\vartheta }_{3}}}{{{c}_{1}}}-\frac{4{{n}^{2}}{{c}_{1}}{{b}_{1}}}{a\left( -1+2n \right) {{r}^{2}}{{\eta }^{2}}c_{0}^{3}},\mu =\frac{-4k\lambda +4{{b}_{8}}+\frac{a\left( 1+2n \right) {{r}^{2}}{{\eta }^{2}}{{\vartheta }_{3}}}{{{n}^{2}}c_{1}^{2}}}{4k}. \\ \end{aligned} \end{aligned}$$
(31)

Using (3), (7), (11), (12), (15), and (31), the following exponential solutions to the present model are acquired:

$$\begin{aligned}{} & {} {{q}_{11}}(x,t)={{\text {e}}^{\text {i}\left( u-kx+\frac{a\left( -{{k}^{2}}+\frac{d{{r}^{2}}}{{{n}^{2}}} \right) {{t}^{\mu }}}{\mu } \right) }}\nonumber \\{} & {} \quad {{\left[ {{c}_{0}}+\frac{4{{c}_{1}}{{\vartheta }_{1}}}{{{\text {e}}^{-r\left( x+\frac{2ak{{t}^{\alpha }}}{\alpha } \right) \eta \sqrt{{{\vartheta }_{1}}}}}-2{{\vartheta }_{2}}+{{\text {e}}^{r\left( x+\frac{2ak{{t}^{\alpha }}}{\alpha } \right) \eta \sqrt{{{\vartheta }_{1}}}}}\left( -4{{\vartheta }_{1}}{{\vartheta }_{3}}+{{\vartheta }_{2}}^{2} \right) } \right] }^{\frac{1}{2n}}}. \end{aligned}$$
(32)

Using (4), (7), (11), (12), (15), and (31), the following hyperbolic solutions to the present model are acquired:

$$\begin{aligned}{} & {} {{q}_{12}}(x,t)={{\text {e}}^{\text {i}\left( u-kx+\frac{w{{t}^{\alpha }}}{\alpha } \right) }}\nonumber \\{} & {} \quad {{\left[ {{c}_{0}}-\frac{{\text {sech}}{{\left[ \frac{r}{2}\eta \sqrt{{{\vartheta }_{1}}}\varsigma \right] }^{2}}{{c}_{1}}{{\vartheta }_{1}}\left( \frac{4{{c}_{0}}{{\vartheta }_{3}}}{{{c}_{1}}}-\frac{4{{n}^{2}}{{c}_{1}}{{b}_{6}}}{a\left( 1+n \right) {{r}^{2}}{{\eta }^{2}}} \right) }{{{\left( \frac{4{{c}_{0}}{{\vartheta }_{3}}}{{{c}_{1}}}-\frac{4{{n}^{2}}{{c}_{1}}{{b}_{6}}}{a\left( 1+n \right) {{r}^{2}}{{\eta }^{2}}} \right) }^{2}}-{{\vartheta }_{1}}{{\vartheta }_{3}}{{\left( 1-\tanh \left[ \frac{r}{2}\eta \sqrt{{{\vartheta }_{1}}}\varsigma \right] \right) }^{2}}} \right] }^{\frac{1}{2n}}}. \end{aligned}$$
(33)

Result-7:

$$\begin{aligned} \begin{aligned}&w=\frac{3a{{r}^{2}}{{\eta }^{2}}c_{0}^{2}{{\vartheta }_{3}}}{4{{n}^{2}}c_{1}^{2}}-a{{k}^{2}}+\frac{3{{b}_{1}}}{\left( -1+2n \right) c_{0}^{2}}-\frac{a{{r}^{2}}{{\eta }^{2}}{{\vartheta }_{1}}}{2{{n}^{2}}}, \\&{{b}_{3}}=-\frac{\left( -1+n \right) \left( c_{1}^{2}\left( 12{{n}^{2}}{{b}_{1}}+a\left( 1-2n \right) {{r}^{2}}{{\eta }^{2}}c_{0}^{2}{{\vartheta }_{1}} \right) +a\left( -1+2n \right) {{r}^{2}}{{\eta }^{2}}c_{0}^{4}{{\vartheta }_{3}} \right) }{4{{n}^{2}}\left( -1+2n \right) {{c}_{0}}c_{1}^{2}}, \\&{{b}_{6}}=\frac{\left( 1+n \right) \left( c_{1}^{2}\left( 4{{n}^{2}}{{b}_{1}}+a\left( 1-2n \right) {{r}^{2}}{{\eta }^{2}}c_{0}^{2}{{\vartheta }_{1}} \right) +3a\left( -1+2n \right) {{r}^{2}}{{\eta }^{2}}c_{0}^{4}{{\vartheta }_{3}} \right) }{4{{n}^{2}}\left( -1+2n \right) c_{0}^{3}c_{1}^{2}}, \\&{{\vartheta }_{2}}=\frac{{{c}_{1}}{{\vartheta }_{1}}}{{{c}_{0}}}+\frac{{{c}_{0}}{{\vartheta }_{3}}}{{{c}_{1}}}-\frac{4{{n}^{2}}{{c}_{1}}{{b}_{1}}}{a\left( -1+2n \right) {{r}^{2}}{{\eta }^{2}}c_{0}^{3}},\mu =\frac{-4k\lambda +4{{b}_{8}}+\frac{a\left( 1+2n \right) {{r}^{2}}{{\eta }^{2}}{{\vartheta }_{3}}}{{{n}^{2}}c_{1}^{2}}}{4k}. \\ \end{aligned} \end{aligned}$$
(34)

Using (3), (7), (11), (12), (15), and (34), the following exponential solutions to the present model are acquired:

$$\begin{aligned}{} & {} {{q}_{13}}(x,t)={{\text {e}}^{\text {i}\left( u-kx+\frac{a{{t}^{\alpha }}\left( c_{1}^{2}\left( -4{{k}^{2}}{{n}^{2}}+{{r}^{2}}{{\eta }^{2}}{{\vartheta }_{1}} \right) -{{L}_{7}} \right) }{4{{n}^{2}}\alpha c_{1}^{2}} \right) }}\nonumber \\{} & {} \quad {{\left[ {{c}_{0}}+\frac{4{{c}_{1}}{{\vartheta }_{1}}}{{{\text {e}}^{-r\eta \varsigma \sqrt{{{\vartheta }_{1}}}}}-2{{\vartheta }_{2}}+{{\text {e}}^{r\varsigma \eta \sqrt{{{\vartheta }_{1}}}}}\left( \vartheta _{2}^{2}-4{{\vartheta }_{1}}{{\vartheta }_{3}} \right) } \right] }^{\frac{1}{2n}}}, \end{aligned}$$
(35)

where \(\varsigma =x+\frac{2ak{{t}^{\alpha }}}{\alpha }\) and \({{L}_{7}}=3{{r}^{2}}{{\eta }^{2}}{{c}_{0}}{{c}_{1}}{{\vartheta }_{2}}+6{{r}^{2}}{{\eta }^{2}}c_{0}^{2}{{\vartheta }_{3}}.\)

Setting the value \({{\vartheta }_{2}}=\sqrt{4{{\vartheta }_{1}}{{\vartheta }_{3}}}\) in the above equation, we obtain

$$\begin{aligned}{} & {} {{q}_{14}}(x,t)={{\text {e}}^{\text {i}\left( u-kx+\frac{a{{t}^{\alpha }}\left( c_{1}^{2}\left( -4{{k}^{2}}{{n}^{2}}+{{r}^{2}}{{\eta }^{2}}{{\vartheta }_{1}} \right) -{{L}_{7}} \right) }{4{{n}^{2}}\alpha c_{1}^{2}} \right) }}\nonumber \\{} & {} \quad {{\left[ {{c}_{0}}+\frac{4{{c}_{1}}{{\vartheta }_{1}}}{{{\text {e}}^{-r\eta \varsigma \sqrt{{{\vartheta }_{1}}}}}-2{{\vartheta }_{2}}+{{\text {e}}^{r\varsigma \eta \sqrt{{{\vartheta }_{1}}}}}\left( \vartheta _{2}^{2}-4{{\vartheta }_{1}}{{\vartheta }_{3}} \right) } \right] }^{\frac{1}{2n}}}. \end{aligned}$$
(36)

Using (4), (7), (11), (12), (15), and (34), the following hyperbolic solutions to the present model are acquired:

$$\begin{aligned}{} & {} {{q}_{15}}(x,t)={{\text {e}}^{\text {i}\left( u-kx+\frac{a{{t}^{\alpha }}\left( c_{1}^{2}\left( {{r}^{2}}{{\eta }^{2}}{{\vartheta }_{1}}-4{{k}^{2}}{{n}^{2}} \right) -{{L}_{7}} \right) }{4{{n}^{2}}\alpha c_{1}^{2}} \right) }}\nonumber \\{} & {} \quad {{\left[ {{c}_{0}}-\frac{{\text {sech}}{{\left[ \frac{1}{2}r\left( x+\frac{2ak{{t}^{\alpha }}}{\alpha } \right) \eta \sqrt{{{\vartheta }_{1}}} \right] }^{2}}{{c}_{1}}{{\vartheta }_{1}}{{\vartheta }_{2}}}{\vartheta _{2}^{2}-{{\vartheta }_{1}}{{\vartheta }_{3}}{{\left( 1-\tanh \left[ \frac{1}{2}r\left( x+\frac{2ak{{t}^{\alpha }}}{\alpha } \right) \eta \sqrt{{{\vartheta }_{1}}} \right] \right) }^{2}}} \right] }^{\frac{1}{2n}}}. \end{aligned}$$
(37)

Results and discussion

In this section, we deliberately selected specific values for the physical parameters to highlight the significance of innovative optical approaches in addressing the conformable nonlinear Schrödinger equation. This equation incorporates Kudryashov’s variable refractive index alongside two distinctive nonlocal nonlinearities. We illustrate the impact of parameters \(\alpha\) and t on the existing soliton solutions through both two-dimensional and three-dimensional graphical representations. Figures 1, 2, 3, 4, 5, 6, 7, 8 and 9, graphs (a) and (b), depict the contour, 3D, and 2D graphs representing the dynamical behavior of the current solutions. The bell-shaped soliton solutions of \({{\left| {{q}_{1}}(x,t) \right| }^{2}}\) is plotted in Fig. 1. graph (a). The bell-shaped and bright optical solitons can be utilized for long-distance communication in optical fibers. Their ability to maintain their shape and amplitude during propagation makes them suitable for preserving data integrity over extended distances. The effect of \(\alpha =1\) and \(\alpha =0.4\) on the wave soliton solutions for the square modulus of \({{q}_{3}}(x,t)\)is illustrated in Fig. 3. graph (a) and graph (b) while the influence of \(\alpha =1\) and \(\alpha =0.5\) on the mixed dark-bright soliton solutions for the square modulus of \({{q}_{7}}(x,t)\) is depicted in Fig. 4. graph (a) and graph (b). In it is clear that in both cases, decreasing the value of conformable parameter \(\alpha\) the solitons take right direction. Thus, dynamical behavior of the soliton’s solutions illustrates the impact of the conformable parameter on the present optical solutions. The same behavior can be noted for the multi-dark soliton solutions for the square modulus of \({{q}_{9}}(x,t)\) in Fig. 5. graph (a) and graph (b). Mixed dark-bright soliton solutions represent a fusion of dark solitons, characterized by localized waves of lower intensity, and bright solitons, characterized by localized waves of higher intensity, existing within a single wave function. This suggests the coexistence of areas with diminished and heightened amplitude or intensity within the same wave, leading to a nuanced interaction between the dark and bright constituents on a physical level. Further, the real and imaginary parts of the conformable optical soliton solutions of \({{q}_{1}}(x,t)\) are wave soliton solutions in Fig. 2. graph (a) and graph (b). Physically, the wave optical soliton solution depicted in these figures may represent a stable and localized waveform propagating through a medium. The square modulus of \({{q}_{10}}(x,t)\) is the dark soliton solution from Fig. 7. graph (a). The dark soliton solutions have various applications in optical fiber systems, including pulse shaping, wavelength division multiplexing, and high-capacity data transmission. By manipulating the parameters governing the propagation of dark solitons, engineers can design optical fiber systems tailored to specific communication needs.

Furthermore, the depiction of the topological characteristics of the soliton solutions concerning variations in the time parameter t is illustrated in Figs. 1b, 6b, and 7b. From these two-dimensional graphs, it is evident that the shapes of various types of solitons remain unchanged over time. Finally, the behavior of the topological aspects of various soliton solutions with changes in the conformable derivative parameter\(\alpha\)is illustrated in Figs. 8a, b, 9a, and b respectively.

Conclusions

The current paper recovered optical soliton solutions to the governing model that came with fractional evolution, linear CD and Kudryasov’s extended power-law and inverse power-law of SPM. Then, Kudryashov’s integration algorithm yielded soliton solutions that can be potentially used to control Internet bottleneck effect by slowing down the solitons using the temporal evolution parameter as the control parameter. Thus, Internet bottleneck effect can be suppressed suing the traffic light effect across junction points. This is one of the three known approaches that can address this technological hurdle with Kudryashov’s form of SPM.

With a success in this mathematical approach to adress the growing telecommunication problem, the model can be addressed further along to study additional features. The next step would be to consider cubic–quartic optical solitons when CD is replaced by the third and fourth-order dispersions collectively. The results of this new project are on their way to the press. This is just a tip of the iceberg. The results will be reported after they are aligned with the preexisting ones [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73].