Introduction

The concept of cubic–quartic optical solitons emerged from the absolute necessity for solitons to sustain during their trans-continental and trans-oceanic transmission when there is a low-count of chromatic dispersion (CD) [1,2,3,4,5,6,7,8,9,10]. This is replenished with the inclusion of third-order dispersion (3OD) and fourth-order dispersion (4OD) terms [11,12,13,14,15,16,17,18,19,20]. One natural question that arises is the soliton slow-down due from the radiative effects that will kick in from third-order and fourth-order dispersions [21,22,23,24,25,26,27,28,29,30]. This is of course tacitly ignored in the paper. The effect of nonlinearity in this paper stems from a specific form of non-Kerr law [31,32,33,34,35,36,37,38,39,40]. The self-phase modulation (SPM) stems from cubic–quintic–septic–nonic form of nonlinear refractive index change. Thus the corresponding governing nonlinear Schrödinger’s equation with such a form of SPM structure will be addressed in the work. The soliton solutions will be retrieved for the model.

While there are several forms of integration algorithms that are visible across the board [41,42,43,44,45,46,47,48,49,50], it must be noted that the most powerful form of integration tool namely the Inverse Scattering Transform will fail for this model. This is apparent due to the failure of the corresponding Painlevé test of integrability. Therefore yet another powerful integration tool will be to the rescue. This is the Lie symmetry analysis. This symmetry analysis will transform the corresponding partial differential equation (PDE) to its corresponding ordinary differential equation (ODE) after decomposing the complex-valued governing model, namely the NLSE, into its real and imaginary components. Subsequently two simple, yet powerful, tools will retrieve the optical soliton solutions to the model. They are the Kudryashov’s auxiliary equation method and the hyperbolic function algorithm. These two approaches would collectively yield a full spectrum of optical solitons that are enumerated in the paper. The details of the model and the soliton solutions derivation are exhibited in the rest of the paper.

Governing model

The propagation of cubic–quartic soliton through optical fibers for intercontinental distances with cubic–quintic–septic–nonic form of SPM is governed by the NLSE that carries the following structure:

$$\begin{aligned} \iota q_t + i aq_{xxx}+bq_{xxxx}+\left( c_1 \left| q \right| ^2 + c_2 \left| q \right| ^4 + c_3 \left| q \right| ^6 + c_4 \left| q \right| ^8\right) q=0. \end{aligned}$$
(1)

The equation discussed in this study represents a wave denoted by q(x, t),  where \(i = \sqrt{-1}\) is the imaginary unit. The coefficients a and b correspond to 3OD and 4OD respectively and they are the replacements of the CD effect. The constants \(c_j\) for \((j = 1, 2, 3, 4)\) represents SPM. The first term in Eq. (1) corresponds to the temporal evolution of the wave, where x represents the spatial variable, and t represents the temporal variable.

Lie symmetry analysis

The Lie symmetry analysis is a powerful mathematical tool for studying dynamical systems. It involves the identification of symmetries in the system’s governing equations and using them to derive invariant solutions and reductions in the number of variables. By understanding the symmetries present in a system, researchers can gain insights into its behavior and make predictions about its future evolution. The Lie symmetry analysis has applications in various fields, from physics and engineering to biology and finance. Overall, it is a valuable tool for understanding the complex dynamics of real-world systems. Lie symmetry analysis, or Lie group analysis, is a mathematical method of studying differential equations. It was developed by the Norwegian mathematician Sophus Lie in the late nineteenth century. Lie was interested in finding methods that could simplify the solution of differential equations, and he realized that many differential equations have symmetries that can be exploited to find solutions.

Lie symmetry analysis is based on the idea that if a differential equation has symmetry, then the solution of the equation can be transformed in a way that preserves the symmetry. This means that if we know the symmetries of a differential equation, we can use them to transform the equation into a simpler form, which is easier to solve. Today, Lie symmetry analysis is still an active area of research, and it continues to be used to solve complex problems in mathematics and physics, including fluid dynamics, electromagnetism, and relativity.

In this section, let’s utilize the Lie symmetry analysis [15,16,17] on Eq. (1). Our initial step would be to consider q(x, t) as

$$\begin{aligned} q(x,t)=\psi (x,t)+\iota \varphi (x,t). \end{aligned}$$
(2)

By following this step, we can transform Eq. (1) into the following system:

$$\begin{aligned} 0&=-\varphi _{t}-a \varphi _{xxx}+b \psi _{xxxx}+ \left( c_1 \left( \psi ^{2}+\varphi ^{2}\right) +c_2 \left( \psi ^{2}+\varphi ^{2}\right) ^{2}\right. \\ &\quad \left. +c_3 \left( \psi ^{2}+\varphi ^{2}\right) ^{3}\right) \psi +c_4 \left( \psi ^{2}+\varphi ^{2}\right) ^{4}\psi ,\\ 0&=\psi _{t}+a \psi _{xxx}+b \varphi _{xxxx}+ \left( c_1 \left( \psi ^{2}+\varphi ^{2}\right) \right. \\ &\quad \left. +c_2 \left( \psi ^{2}+\varphi ^{2}\right) ^{2}+c_3 \left( \psi ^{2}+\varphi ^{2}\right) ^{3}\right) \varphi \\ &\quad +c_4 \left( \psi ^{2}+\varphi ^{2}\right) ^{4}\varphi . \end{aligned}$$
(3)

Let’s assume the following Lie group of point transformation to derive symmetries for system (3).

$$\begin{aligned} x^*&=x+\epsilon \ \xi (x,t,\psi ,\varphi )+O(\epsilon ^2),\\ t^*&=t+\epsilon \ \tau (x,t,\psi ,\varphi )+O(\epsilon ^2),\\ \psi ^*&=\psi +\epsilon \ \eta (x,t,\psi ,\varphi )+O(\epsilon ^2),\\ \varphi ^*&=\varphi +\epsilon \ \phi (x,t,\psi ,\varphi )+O(\epsilon ^2). \end{aligned}$$
(4)

We need to determine the values of infinitesimals \(\xi ,\) \(\tau ,\) \(\eta ,\) and \(\phi\) for the transformation given by (4). The vector field corresponding to this transformation is to be found.

$$\begin{aligned} V=\xi \partial _x+\tau \partial _t+\eta \partial _\psi +\phi \partial _\varphi . \end{aligned}$$
(5)

The given system (3) has a fourth prolongation formula for vector field (5).

$$\begin{aligned} Pr^{(4)}V&= V+\eta ^t\frac{\partial }{\partial \psi _t}+\phi ^t\frac{\partial }{\partial \varphi _t}+\eta ^{xxx}\frac{\partial }{\partial \psi _{xxx}} \\ & \quad +\phi ^{xxx}\frac{\partial }{\partial \varphi _{xxx}}+\eta ^{xxxx}\frac{\partial }{\partial \psi _{xxxx}}+\phi ^{xxxx}\frac{\partial }{\partial \varphi _{xxxx}}. \end{aligned}$$
(6)

We can incorporate extended infinitesimals \(\eta ^{t},\phi ^{t},\eta ^{xxx},\phi ^{xxx},\eta ^{xxxx}\) and \(\phi ^{xxxx}\) into the system. Furthermore, we can utilize the invariance conditions \(Pr^{(4)}V(\Delta )=0,\) which hold true whenever \(\Delta = 0\) in system (3). Through this approach, we were able to obtain

$$\begin{aligned} 0&= -\phi ^t-a\phi ^{xxx}+b\eta ^{xxxx}+\eta [c_1(3\psi ^2+\varphi ^2)\\ &\quad +c_2((\psi ^2+\varphi ^2)(5\psi ^2+\varphi ^2))\\ &\quad +c_3((\psi ^2+\varphi ^2)^2(7\psi ^2+\varphi ^2))\\ &\quad +c_4((\psi ^2+\varphi ^2)^3(9\psi ^2+\varphi ^2))]\\ &\quad +\phi [2uvc_1+2\psi \varphi (\psi ^2+\varphi ^2)(2c_2\\ &\quad +3c_3(\psi ^2+\varphi ^2)+4c_4(\psi ^2+\varphi ^2)],\\ 0&=\eta ^t+a\eta ^{xxx}+b\phi ^{xxxx}+\phi [c_1(\psi ^2+3\varphi ^2)\\ &\quad +c_2((\psi ^2+\varphi ^2)(\psi ^2+5\varphi ^2))\\ &\quad +c_3((\psi ^2+\varphi ^2)^2(\psi ^2+7\varphi ^2))\\ &\quad +c_4((\psi ^2+\varphi ^2)^3(\psi ^2+9\varphi ^2))]\\ &\quad +\eta [2uvc_1+2\psi \varphi (\psi ^2+\varphi ^2)(2c_2+3c_3(\psi ^2\\ &\quad +\varphi ^2)+4c_4(\psi ^2+\varphi ^2)]. \end{aligned}$$
(7)

Upon substitution of the values of infinitesimals \(\eta ^{t},\phi ^{t},\eta ^{xxx},\phi ^{xxx},\eta ^{xxxx}\) and \(\phi ^{xxxx}\) and equating the coefficients of different derivative terms to zero, a complex system of equations is derived. By solving this system, we can determine the values of infinitesimals as follows:

$$\begin{aligned} \xi =C_1,\quad \tau =C_2,\quad \eta =C_3\varphi ,\quad \phi =-C_3\psi . \end{aligned}$$
(8)

Since \(C_1,\) \(C_2\) and \(C_3\) are arbitrary constants, and we can conclude that the Lie algebra of system (3) is traversed by the following infinitesimal generators.

$$\begin{aligned} V_1&= \frac{\partial }{\partial x},\quad V_2=\frac{\partial }{\partial t}, \\ V_3&= \varphi \frac{\partial }{\partial \psi }-\psi \frac{\partial }{\partial \varphi }. \end{aligned}$$
(9)

We will consider the following vector field

$$\begin{aligned} \mu V_1+\lambda V_2+ V_3=\mu \frac{\partial }{\partial x} +\lambda \frac{\partial }{\partial t}+\left( \varphi \frac{\partial }{\partial \psi }-\psi \frac{\partial }{\partial \varphi }\right) . \end{aligned}$$
(10)

Since \(\lambda\) and \(\mu\) are arbitrary non-zero real numbers, it is possible to solve the characteristic equation.

$$\begin{aligned} \frac{dx}{\xi }=\frac{dt}{\tau }=\frac{d\psi }{\eta }=\frac{d\varphi }{\phi }. \end{aligned}$$
(11)

We can obtain the similarity variables by relating them to the vector field (10) in the following manner:

$$\begin{aligned} q(x,t)=P(\sigma )e^{iQ(x,t)},\quad \sigma =\mu x-\lambda t, \quad Q(x,t)= kx-\omega t +\theta , \end{aligned}$$
(12)

where P is the new dependent variable.

To find the real part, we can substitute the value of Eq. (12) into Eq. (1). This will give us the desired result.

$$\begin{aligned} 0&=b \mu ^{4} P''''-\left( 6 \mu ^{2} k^{2} b+3 \mu ^{2} a k\right) P''+\left( b \,k^{4}+a \,k^{3}+\omega \right) P\\ &\quad +c_{1}P^{3}+c_{2}P^{5}+c_{3}P^{7}+ c_{4}P^{9}, \end{aligned}$$
(13)

and the imaginary part as

$$\begin{aligned} 0=\mu ^{3} \left( 4 b k+a\right) P'''+ \left( -4 b \,k^{3} \mu -3 a \,k^{2} \mu -\lambda \right) P. \end{aligned}$$
(14)

Suppose that \(a=-4bk, \ \lambda =-4bk^3\mu -3ak^2\mu ,\) and let

$$\begin{aligned} P(\sigma )=\sqrt{U(\sigma )}, \end{aligned}$$
(15)

then, Eq. (13) can be modified as

$$\begin{aligned}&15 b \mu ^{4}U'^{4}-36 b \mu ^{4}U U'^{2} U''-24 b \,k^{2} \mu ^{2}U^{2} U'^{2}\\ &\quad +16 b \mu ^{4}U^{2} U'U''' +12 b \mu ^{4}U^{2} U''^{2}+48 b \,k^{2} \mu ^{2} U^{3} U''\\ &\quad -8 b \mu ^{4}U^{3} U''''-16 c_{4} U^{8}-16 b \,k^{4} U^{4}\\ &\quad -12 a k \mu ^{2}U^{2} U'^{2} +24 a k \mu ^{2} U^{3} U''\\ &\quad -16 c_{3} U^{7}-16a \,k^{3} U^{4} -16 c_{2} U^{6}-16 c_{1} U^{5}-16 U^{4} \omega =0. \end{aligned}$$
(16)

Hyperbolic function algorithm

Hyperbolic functions are a set of mathematical functions that are related to the standard trigonometric functions. They are used extensively in mathematical analysis, physics, and engineering. The hyperbolic function algorithm is a set of instructions that can be used to calculate hyperbolic functions for any given input. The hyperbolic function algorithm is an essential tool for solving various mathematical problems in multiple fields. In this section, we will obtain soliton solutions of Eq. (1) by employing hyperbolic function method on Eq. (16). This section will explore two different approaches for extracting solitons from nonlinear partial differential equations. To organize our discussion, we will divide the section into two subsections. The first subsection deals with extracting dark and singular solitons. This approach assumes the solution structure in terms of the tanh function. This method can effectively identify and extract dark and singular solitons from the given equation. The second subsection deals with extracting bright and singular solitons. This approach assumes the solution structure in terms of the sech function. This method can effectively identify and extract bright and singular solitons from the given equation. Applying these methods can recover bright, dark, and singular solitons from nonlinear partial differential equations. These schemes are easy to implement and convenient for practical applications. Moreover, they have proven effective in identifying and extracting solitons from various types of nonlinear partial differential equations, making them a valuable tool for researchers and engineers in many fields.

Tanh–coth approach

From the tanh–coth scheme [18,19,20], the soliton solution of Eq. (16), is of the form

$$\begin{aligned} U(\sigma )=A_0+A_1 \text{tanh}(m\sigma )+\cdots +A_n\text{tanh}^n(m\sigma ), \end{aligned}$$
(17)

where \(A_{0},A_{1}\ldots A_{n}\) are arbitrary constants. By balancing \(U^{3} U''''\) and \(U^{8}\) from Eq. (16), we obtain \(n=1.\) Now substituting the value from Eq. (17) into (16) and by collecting and equating the terms of different powers of tanh to zero, we obtain the following system of equations:

$$\begin{aligned} 0&=-105 A_{1}^{4} m^{4} b \mu ^{4}-16 c_{4} A_{1}^{8}, \\ 0&=-360 A_{0} A_{1}^{3} m^{4} b \mu ^{4}-128 c_{4} A_{0} A_{1}^{7}-16 c_{3} A_{1}^{7}, \\ 0&=-424 A_{0} A_{1}^{3} m^{4} b \mu ^{4}+240 A_{0} A_{1}^{3} m^{2} b \,k^{2} \mu ^{2} \\ &\quad -8 (24 A_{0}^{3} A_{1} m^{4}-120 A_{0} A_{1}^{3} m^{4}) b \mu ^{4} \\ &\quad - 896 c_{4} A_{0}^{3} A_{1}^{5}+120 A_{0} A_{1}^{3} m^{2} a k \mu ^{2} \\ &\quad - 336 c_{3} A_{0}^{2} A_{1}^{5}-96 c_{2} A_{0} A_{1}^{5}-16 c_{1} A_{1}^{5}, \\ 0&=156 A_{1}^{4} m^{4} b \mu ^{4}+72 A_{1}^{4} m^{2} b \,k^{2} \mu ^{2} \\ &\quad +16 (-6 (-A_{0}^{2} A_{1} m+A_{1}^{3} m) A_{1} m^{3}-8 A_{1}^{4} m^{4}) b \mu ^{4} \\ &\quad +48 (A_{0}^{2} A_{1}^{2} m^{4}-2 A_{1}^{4} m^{4}) b \mu ^{4}-8 (72 A_{0}^{2} A_{1}^{2} m^{4} \\ &\quad -40 A_{1}^{4} m^{4}) b \mu ^{4}-448 c_{4} A_{0}^{2} A_{1}^{6}+36 A_{1}^{4} m^{2} a k \mu ^{2} \\ &\quad -112 c_{3} A_{0} A_{1}^{6}-16 c_{2} A_{1}^{6} B_{1}^{3}+A_{6}B_{1}^{3} \\ &\quad +50A_{1}B_{1}+2A_{4}B_{1}, \\ 0&=-126 A_{1}^{4} m^{4} b \mu ^{4}-24 (A_{0}^{2} A_{1}^{2} m^{2}-2 A_{1}^{4} m^{2}) b \,k^{2} \mu ^{2} \\ &\quad +16 (-6 A_{0}^{2} A_{1}^{2} m^{4}+8 (-A_{0}^{2} A_{1} m \\ &\quad + A_{1}^{3} m) A_{1} m^{3}+2 A_{1}^{4} m^{4}) b \mu ^{4}+ 48 (-2 A_{0}^{2} A_{1}^{2} m^{4} \\ &\quad +A_{1}^{4} m^{4}) b \mu ^{4}-96 (-3 A_{0}^{2} A_{1}^{2} m^{2} \\ &\quad +A_{1}^{4} m^{2}) b \,k^{2} \mu ^{2}-8 (-120 A_{0}^{2} A_{1}^{2} m^{4}+16 A_{1}^{4} m^{4}) b \mu ^{4} \\ &\quad -1120 c_{4} A_{0}^{4} A_{1}^{4}-16 A_{1}^{4} b \,k^{4}- 12 (A_{0}^{2} A_{1}^{2} m^{2}-2 A_{1}^{4} m^{2}) a k \mu ^{2} \\ &\quad -48 (-3 A_{0}^{2} A_{1}^{2} m^{2}+A_{1}^{4} m^{2}) a k \mu ^{2}-560 c_{3} A_{0}^{3} A_{1}^{4} \\ &\quad - 16 A_{1}^{4} a \,k^{3}-240 c_{2} A_{0}^{2} A_{1}^{4}- 80 c_{1} A_{0} A_{1}^{4}-16 A_{1}^{4} \omega , \\ 0&=200 A_{0} A_{1}^{3} m^{4} b \mu ^{4}+96 A_{0} A_{1}^{3} m^{2} b \,k^{2} \mu ^{2} \\ &\quad -96 (-A_{0}^{3} A_{1} m^{2}+3 A_{0} A_{1}^{3} m^{2}) b \,k^{2} \mu ^{2} \\ &\quad -8 (-40 A_{0}^{3} A_{1} m^{4}+48 A_{0} A_{1}^{3} m^{4}) b \mu ^{4} \\ &\quad - 896 c_{4} A_{0}^{5} A_{1}^{3}-64 A_{0} A_{1}^{3} b \,k^{4}+48 A_{0} A_{1}^{3} m^{2} a k \mu ^{2} \\ &\quad - 48 (-A_{0}^{3} A_{1} m^{2}+3 A_{0} A_{1}^{3} m^{2}) a k \mu ^{2}-560 c_{3} A_{0}^{4} A_{1}^{3} \\ &\quad -64 A_{0} A_{1}^{3} a \,k^{3}- 320 c_{2} A_{0}^{3} A_{1}^{3} \\ &\quad -160 c_{1} A_{0}^{2} A_{1}^{3}-64 A_{0} A_{1}^{3} \omega , \\ 0&=12 A_{1}^{4} m^{4} b \mu ^{4}-24 (-2 A_{0}^{2} A_{1}^{2} m^{2}+A_{1}^{4} m^{2}) b \,k^{2} \mu ^{2} \\ &\quad +16 (8 A_{0}^{2} A_{1}^{2} m^{4}-2 (-A_{0}^{2} A_{1} m \\ &\quad +A_{1}^{3} m) A_{1} m^{3}) b \mu ^{4}-336 A_{0}^{2} A_{1}^{2} m^{4} b \mu ^{4} \\ &\quad - 288 A_{0}^{2} A_{1}^{2} m^{2} b \,k^{2} \mu ^{2}-448 c_{4} A_{0}^{6} A_{1}^{2} \\ &\quad -96 A_{0}^{2} A_{1}^{2} b \,k^{4}-12 (-2 A_{0}^{2} A_{1}^{2} m^{2}+A_{1}^{4} m^{2}) a k \mu ^{2} \\ &\quad -144 A_{0}^{2} A_{1}^{2} m^{2} a k \mu ^{2}-336 c_{3} A_{0}^{5} A_{1}^{2} \\ &\quad -96 A_{0}^{2} A_{1}^{2} a \,k^{3}-240 c_{2} A_{0}^{4} A_{1}^{2} \\ &\quad -160 c_{1} A_{0}^{3} A_{1}^{2}-96 A_{0}^{2} A_{1}^{2} \omega , \\ 0&=-128 A_{0}^{3} A_{1} m^{4} b \mu ^{4}+8 A_{0} A_{1}^{3} m^{4} b \mu ^{4} \\ &\quad -96 A_{0}^{3} A_{1} m^{2} b \,k^{2} \mu ^{2}-48 A_{0} A_{1}^{3} m^{2} b \,k^{2} \mu ^{2} \\ &\quad - 48 A_{0}^{3} A_{1} m^{2} a k \mu ^{2}-24 A_{0} A_{1}^{3} m^{2} a k \mu ^{2}-128 c_{4} A_{0}^{7} A_{1} \\ &\quad -64 A_{0}^{3} A_{1} b \,k^{4}-112 c_{3} A_{0}^{6} A_{1} \\ &\quad -64 A_{0}^{3} A_{1} a \,k^{3}-96 c_{2} A_{0}^{5} A_{1}-80 c_{1} A_{0}^{4} A_{1}-64 A_{0}^{3} A_{1} \omega , \\ 0&=32 A_{0}^{2} A_{1}^{2} m^{4} b \mu ^{4}+15 A_{1}^{4} m^{4} b \mu ^{4} \\ &\quad -24 A_{0}^{2} A_{1}^{2} m^{2} b \,k^{2} \mu ^{2}-12 A_{0}^{2} A_{1}^{2} m^{2} a k \mu ^{2}-16 c_{4} A_{0}^{8} \\ &\quad - 16 A_{0}^{4} b \,k^{4}-16 c_{3} A_{0}^{7}-16 A_{0}^{4} a \,k^{3}- 16 c_{2} A_{0}^{6} \\ &\quad -16 c_{1} A_{0}^{5}-16 A_{0}^{4} \omega . \end{aligned}$$
(18)

The system of algebraic equations has been successfully solved, and the resulting set of solutions is as follows:

$$\begin{aligned} A_{0}&= \pm A_{1},\\ c_{1}&= \pm \frac{2 \left( 27 \Psi a k+2b\left( 27 \Psi k^{2}-10 b \,k^{4}-10 a \,k^{3}-10 \omega \right) \right) }{2bA_{1}},\\ c_{2}&=-\frac{3 \left( 171 \Psi a k+2b(171 \Psi k^{2}-58 b \,k^{4}-58 a \,k^{3}-58 \omega )\right) }{8b A_{1}^{2}},\\ c_{3}&=\pm \frac{30 \left( 3 \Psi a k+2b(3 \Psi k^{2}-b \,k^{4}-a \,k^{3}-\omega )\right) }{2bA_{1}^{3}},\\ c_{4}&=-\frac{105 \left( 3 \Psi a k+2b(3 \Psi k^{2}-b \,k^{4}-a \,k^{3}-\omega )\right) }{32b A_{1}^{4}},\\ m&= \pm \frac{1}{\mu }\sqrt{\frac{\Psi }{2b}}, \end{aligned}$$
(19)

where \(\Psi\) is defined as

$$\begin{aligned} \Psi =6 b \,k^{2}+3 a k+\sqrt{32 b^{2} k^{4}+32 a b \,k^{3}+9 a^{2} k^{2}-4 b \omega } \end{aligned}$$

and \(\Psi b>0.\) From the Eq. (19) solutions of the Eq. (16) can be written as

$$\begin{aligned} U(\sigma )=A_1\left( \pm 1+\text{tanh}\left( \pm \frac{1}{\mu }\sqrt{\frac{\Psi }{2b}}\sigma \right) \right) . \end{aligned}$$
(20)

From the Eqs. (12), (15) and (20), the dark soliton solutions of Eq. (1) can be written as

$$\begin{aligned} q(x,t)=\left( \sqrt{A_1\left( \pm 1+\text{tanh}\left( \pm \frac{1}{\mu }\sqrt{\frac{\Psi }{2b}}(\mu x-\lambda t)\right) \right) }\right) e^{\iota (kx-\omega t+\theta )}. \end{aligned}$$
(21)

By the same process, we can have singular soliton solutions of Eq. (1) as

$$\begin{aligned} q(x,t)=\left( \sqrt{A_1\left( \pm 1+\text{coth}\left( \pm \frac{1}{\mu }\sqrt{\frac{\Psi }{2b}}(\mu x-\lambda t)\right) \right) }\right) e^{\iota (kx-\omega t+\theta )}. \end{aligned}$$
(22)

Sech function scheme

Sech scheme [18,19,20] suggests that the soliton solution of Eq. (16) is of the form

$$\begin{aligned} U(\sigma )=A_0+A_1 \text{sech}(m\sigma )+\ldots +A_n\text{sech}^n(m\sigma ), \end{aligned}$$
(23)

where \(A_0,A_1 \ldots A_n\) are arbitrary constants.

By balancing \(U^{3} U''''\) and \(U^{8}\) of Eq. (16), we obtain \(n=1.\) Now substituting the value from Eq. (23) into (16) and by collecting and equating the terms of different powers of sech to zero, we obtain the following system of equations:

$$\begin{aligned} 0&=-105 A_{1}^{4} m^{4} b \mu ^{4}-16 c_{4} A_{1}^{8}, \\ 0&=-360 A_{0} A_{1}^{3} m^{4} b \mu ^{4}-128 c_{4} A_{0}A_{1}^{7}-16 c_{3} A_{1}^{7} , \\ 0&=16 c_{4} A_{0}^{8}-16 A_{0}^{4} b \,k^{4}-16 c_{3} A_{0}^{7}-16 A_{0}^{4} a\,k^{3} \\ &\quad -16 c_{2} A_{0}^{6}-16 c_{1} A_{0}^{5}-16 A_{0}^{4} \omega , \\ 0&=-432 A_{0}^{2} A_{1}^{2} m^{4} b \mu ^{4}+78 A_{1}^{4} m^{4} b \mu ^{4}-72 A_{1}^{4} m^{2} b \,k^{2} \mu ^{2} \\ &\quad -36 A_{1}^{4} m^{2} a k \mu ^{2}-448 c_{4} A_{0}^{2} A_{1}^{6} \\ &\quad -112 c_{3} A_{0} A_{1}^{6}-16 c_{2} A_{1}^{6}, \\ 0&=-192 A_{0}^{3} A_{1} m^{4} b \mu ^{4}+268 A_{0} A_{1}^{3} m^{4} b \mu ^{4} \\ &\quad -240 A_{0}A_{1}^{3} m^{2} b \,k^{2} \mu ^{2}-120 A_{0} A_{1}^{3} m^{2} a k \mu ^{2} \\ &\quad -896 c_{4} A_{0}^{3} A_{1}^{5}-336 c_{3} A_{0}^{2} A_{1}^{5}-96 c_{2} A_{0} A_{1}^{5}-16 c_{1} A_{1}^{5}, \\ 0&=320 A_{0}^{2} A_{1}^{2} m^{4} b \mu ^{4}-A_{1}^{4} m^{4} b \mu ^{4}-264 A_{0}^{2} A_{1}^{2} m^{2} b \,k^{2} \mu ^{2} \\ &\quad +24 A_{1}^{4} m^{2} b \,k^{2} \mu ^{2} \\ &\quad -132 A_{0}^{2} A_{1}^{2} m^{2} a k \mu ^{2}+12 A_{1}^{4} m^{2}a k \mu ^{2} \\ &\quad -1120 c_{4} A_{0}^{4} A_{1}^{4}-16 A_{1}^{4} b \,k^{4}- 560 c_{3} A_{0}^{3} A_{1}^{4} \\ &\quad -16 A_{1}^{4} a \,k^{3}-240 c_{2} A_{0}^{2} A_{1}^{4}-80 c_{1} A_{0} A_{1}^{4}-16 A_{1}^{4} \omega , \\ 0&=160 A_{0}^{3} A_{1} m^{4} b \mu ^{4}-4 A_{0} A_{1}^{3} m^{4} b \mu ^{4} \\ &\quad -96 A_{0}^{3} A_{1} m^{2} b\,k^{2} \mu ^{2}+96 A_{0} A_{1}^{3} m^{2} b \,k^{2} \mu ^{2} \\ &\quad -64 A_{0} A_{1}^{3} \omega -48 A_{0}^{3} A_{1} m^{2} a k \mu ^{2} \\ &\quad +48 A_{0} A_{1}^{3} m^{2} a k \mu ^{2}-896 c_{4} A_{0}^{5} A_{1}^{3}- 64 A_{0} A_{1}^{3} b \,k^{4} \\ &\quad -560 c_{3} A_{0}^{4} A_{1}^{3}-64 A_{0} A_{1}^{3} a\,k^{3} \\ &\quad -320 c_{2} A_{0}^{3} A_{1}^{3}-160 c_{1} A_{0}^{2} A_{1}^{3}, \\ 0&=4 A_{0}^{2} A_{1}^{2} m^{4} b \mu ^{4}+120 A_{0}^{2} A_{1}^{2} m^{2} b \,k^{2} \mu ^{2} \\ &\quad +60 A_{0}^{2} A_{1}^{2} m^{2} a k \mu ^{2}-448 c_{4} A_{0}^{6} A_{1}^{2}-96 A_{0}^{2} A_{1}^{2} b \,k^{4} \\ &\quad -336 c_{3} A_{0}^{5} A_{1}^{2}-96 A_{0}^{2} A_{1}^{2} a \,k^{3}-240 c_{2} A_{0}^{4} A_{1}^{2} \\ &\quad -160c_{1} A_{0}^{3} A_{1}^{2}-96 A_{0}^{2} A_{1}^{2} \omega , \\ 0&=-8 A_{0}^{3} A_{1} m^{4} b \mu ^{4}+48 A_{0}^{3} A_{1} m^{2} b \,k^{2} \mu ^{2} \\ &\quad +24 A_{0}^{3} A_{1} m^{2} a k \mu ^{2}-128 c_{4} A_{0}^{7} A_{1}-64 A_{0}^{3} A_{1} b \,k^{4} \\ &\quad -112 c_{3} A_{0}^{6} A_{1}-64 A_{0}^{3} A_{1} a\,k^{3} \\ &\quad -96 c_{2} A_{0}^{5} A_{1}-80 c_{1} A_{0}^{4} A_{1}-64 A_{0}^{3} A_{1} \omega . \end{aligned}$$
(24)

After solving the above system of algebraic equations, we have the following sets of solutions

Case A

$$\begin{aligned} A_{0}&=\pm A_{1},\\ c_{1}&=\pm \left( \frac{8 \left( 612 k^{2}b \alpha +306 a k \alpha +121b(65 b \,k^{4}+65 a \,k^{3}+65 \omega ) \right) }{-14641b A_{1}}\right) ,\\ c_{2}&=\frac{9 \left( 4676 k^{2}b \alpha +2338 a k \alpha +121b(344 b \,k^{4}+344 a \,k^{3}+344 \omega )\right) }{58564b A_{1}^{2}},\\ c_{3}&=\pm \left( \frac{120 \left( 60 k^{2}b \alpha +30 a k \alpha +121b(4 b \,k^{4}+4 a \,k^{3}+4 \omega )\right) }{-14641b A_{1}^{3}}\right) ,\\ c_{4}&=\frac{105 \left( 60 k^{2}b \alpha +30 a k \alpha +121b(4 b k^{4}+4 a k^{3}+4 \omega ) \right) }{58564b A_{1}^{4}},\\ m&=\pm \frac{1}{11 \mu } \sqrt{\frac{2 \alpha }{b}}, \end{aligned}$$
(25)

where \(\alpha\) is defined as

$$\begin{aligned} \alpha =-30 b \,k^{2}-15 a k+\sqrt{416 b^{2} k^{4}+416 a b \,k^{3}+225 a^{2} k^{2}-484 b \omega } \end{aligned}$$

and \(\alpha b>0.\) From Eq. (25), solution of the Eq. (16) can be written as

$$\begin{aligned} U(\sigma )=A_1\left( \pm 1+\text{sech}\left( \pm \frac{1}{11 \mu } \sqrt{\frac{2 \alpha }{b}}\sigma \right) \right) . \end{aligned}$$
(26)

From the Eqs. (12), (15) and (26), the soliton solution of Eq. (1) can be written as

$$\begin{aligned} q(x,t)=\left( \sqrt{A_1\left( \pm 1+\text{sech}\left( \pm \frac{1}{11 \mu } \sqrt{\frac{2 \alpha }{b}}(\mu x-\lambda t)\right) \right) }\right) e^{\iota (kx-\omega t+\theta )}. \end{aligned}$$
(27)
Fig. 1
figure 1

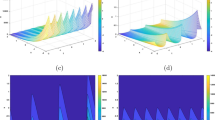
3D and 2D plot representations of the solution (27) with positive amplitude

Full size image
Fig. 2
figure 2

3D and 2D plot representations of the solution (27) with negative amplitude

Full size image

Case B

$$\begin{aligned} A_{0}&=c_1=c_3= 0,\\ c_{2}&=\frac{3 \left( 300 b\Psi k^{2}+150 \Psi a k-b(104 b \,k^{4}-104 a \,k^{3}-104 \omega ) \right) }{4b A_{1}^{2}},\\ c_{4}&=-\frac{105 \left( 12 b\Psi k^{2}+6 \Psi a k-b(4 b \,k^{4}-4 a \,k^{3}-4 \omega ) \right) }{4b A_{1}^{4}},\\ m&=\pm \frac{1}{\mu }\sqrt{\frac{2\Psi }{b}}, \end{aligned}$$
(28)

where \(\Psi\) is defined as

$$\begin{aligned} \Psi =6 b \,k^{2}+3 a k+\sqrt{32 b^{2} k^{4}+32 a b \,k^{3}+9 a^{2} k^{2}-4 b \omega }. \end{aligned}$$

From Eq. (28) the solutions of the Eq. (16) can be written as

$$\begin{aligned} U(\sigma )=A_1\text{sech}\left( \pm \frac{1}{\mu }\sqrt{\frac{2\Psi }{b}} \sigma \right) . \end{aligned}$$
(29)

From the Eqs. (12), (15) and (29), the soliton solution of Eq. (1) can be written as

$$\begin{aligned} q(x,t)=\left( \sqrt{A_1\text{sech}\left( \pm \frac{1}{\mu }\sqrt{\frac{2\Psi }{b}}(\mu x-\lambda t)\right) }\right) e^{\iota (kx-\omega t+\theta )}. \end{aligned}$$
(30)
Fig. 3
figure 3

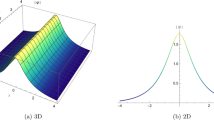
3D and 2D plot representations of the solution (30) with positive amplitude

Full size image
Fig. 4
figure 4

3D and 2D plot representations of the solution (30) with negative amplitude

Full size image

Kudryashov’s auxiliary equation method

An effective method namely, Kudryashov auxiliary equation method [21], is applied in this section to obtain some more soliton solutions. The Kudryashov auxiliary equation method is a mathematical technique to find exact solutions to nonlinear partial differential equations (PDEs). It involves introducing an auxiliary equation related to the original PDE and solving it to obtain solutions that can then be used to determine the solutions of the original equation. This method is particularly useful for finding explicit solutions of nonlinear PDEs that cannot be solved using traditional analytical methods. The Kudryashov method has been successfully applied to various nonlinear PDEs in physics, engineering, and other fields.

Suppose that the soliton solution of Eq. (16), is of the form

$$\begin{aligned} U(\sigma )=A_0+A_1 R(\sigma ), \end{aligned}$$
(31)

where \(A_0\) and \(A_1\) are arbitrary constants where \(A_1 \ne 0,\) and \(R(\sigma )\) satisfies

$$\begin{aligned} (R'(\sigma ))^2=R^2(\sigma )(f-gR(\sigma )-hR^2(\sigma )) \end{aligned}$$
(32)

and has of the form

$$\begin{aligned} R(\sigma )= \frac{4 f}{\left( 4 f h+g^{2}\right) {\textrm{e}}^{\sigma \mathrm {\sqrt{f}}}+2 g+{\textrm{e}}^{-\sigma \mathrm {\sqrt{f}}}}. \end{aligned}$$
(33)

Substituting Eqs. (31) and (32) into Eq. (16) and equating the coefficients of different powers of \(R(\sigma )\) to zero, we obtain

$$\begin{aligned} 0&=-105 A_{1}^{4} b \,h^{2} \mu ^{4}-16 A_{1}^{8} c_{4}, \\ 0&= -360 A_{1}^{3} b \mu ^{4} A_{0} h^{2}-120 A_{1}^{4} b \mu ^{4} g h \\ &\quad -128 A_{0} A_{1}^{7} c_{4}-16 A_{1}^{7} c_{3}, \\ 0&=-432 A_{1}^{2} b \mu ^{4} A_{0}^{2} h^{2}-414 A_{1}^{3} b \mu ^{4} A_{0} g h \\ &\quad +78 A_{1}^{4} b \mu ^{4} f h-24 A_{1}^{4} b \mu ^{4} g^{2}-72 A_{1}^{4} b \,k^{2} \mu ^{2} h \\ &\quad -448 A_{0}^{2} A_{1}^{6} c_{4}-36 A_{1}^{4} a k \mu ^{2} h-112 A_{0} A_{1}^{6} c_{3}-16 A_{1}^{6} c_{2}, \\ 0&=-192 A_{1} b \mu ^{4} A_{0}^{3} h^{2}-504 A_{1}^{2} b \mu ^{4} A_{0}^{2} g h \\ &\quad +268 A_{1}^{3}b \mu ^{4} A_{0} f h-84 A_{1}^{3} b \mu ^{4} A_{0} g^{2}+20 A_{1}^{4} b \mu ^{4} f g \\ &\quad -240 A_{1}^{3} b \,k^{2} \mu ^{2} A_{0} h-48 A_{1}^{4} b\,k^{2} \mu ^{2} g \\ &\quad -896 A_{0}^{3} A_{1}^{5} c_{4}-120 A_{1}^{3}a k \mu ^{2} A_{0} h \\ &\quad -24 A_{1}^{4} a k \mu ^{2} g \\ &\quad -336 A_{0}^{2} A_{1}^{5} c_{3}-96 A_{0} A_{1}^{5} c_{2}-16 A_{1}^{5} c_{1}, \\ 0&=-8 A_{1} b \mu ^{4} A_{0}^{3} f^{2}+48 A_{1} b \,k^{2} \mu ^{2} A_{0}^{3} f \\ &\quad -128 A_{0}^{7} A_{1} c_{4}+24 A_{1} a k \mu ^{2} A_{0}^{3} f-64 A_{0}^{3} A_{1} b \,k^{4} \\ &\quad -112 A_{0}^{6} A_{1} c_{3}-64 A_{0}^{3} A_{1}a \,k^{3} \\ &\quad -96 A_{0}^{5} A_{1} c_{2}-80 A_{0}^{4} A_{1} c_{1}-64 A_{0}^{3} A_{1} \omega , \\ 0&=-240 A_{1} b \mu ^{4} A_{0}^{3} g h+320 A_{1}^{2} b \mu ^{4} A_{0}^{2}f h \\ &\quad -105 A_{1}^{2} b \mu ^{4} A_{0}^{2} g^{2} \\ &\quad +70 A_{1}^{3}b \mu ^{4} A_{0} f g-A_{1}^{4} b \mu ^{4} f^{2} \\ &\quad -264 A_{1}^{2} b \,k^{2} \mu ^{2} A_{0}^{2} h-168 A_{1}^{3} b \,k^{2} \mu ^{2} A_{0} g \\ &\quad +24 A_{1}^{4} b \,k^{2} \mu ^{2} f-1120 A_{0}^{4} A_{1}^{4}c_{4} \\ &\quad -132 A_{1}^{2} a k \mu ^{2} A_{0}^{2} h \\ &\quad -84 A_{1}^{3} a k \mu ^{2} A_{0} g+12 A_{1}^{4} a k \mu ^{2} f \\ &\quad -16 A_{1}^{4} b \,k^{4}-560 A_{0}^{3} A_{1}^{4} c_{3}-16 A_{1}^{4} a \,k^{3}-240 A_{0}^{2} A_{1}^{4} c_{2} \\ &\quad -80 A_{0} A_{1}^{4} c_{1}-16 A_{1}^{4} \omega , \\ 0&=160 A_{1} b \mu ^{4} A_{0}^{3} f h-60 A_{1} b \mu ^{4} A_{0}^{3} g^{2}+80 A_{1}^{2} b\mu ^{4} A_{0}^{2} f g \\ &\quad -4 A_{1}^{3} b \mu ^{4} A_{0} f^{2}-96 A_{1} b \,k^{2} \mu ^{2} A_{0}^{3} h \\ &\quad -192 A_{1}^{2} b \,k^{2} \mu ^{2} A_{0}^{2} g+96 A_{1}^{3} b \,k^{2} \mu ^{2} A_{0} f-896 A_{0}^{5} A_{1}^{3} c_{4} \\ &\quad -48 A_{1}a k \mu ^{2} A_{0}^{3} h-96 A_{1}^{2} a k \mu ^{2} A_{0}^{2} g \\ &\quad +48 A_{1}^{3} a k \mu ^{2} A_{0} f-64 A_{0} A_{1}^{3} b \,k^{4}-560 A_{0}^{4} A_{1}^{3} c_{3}-64 A_{0} A_{1}^{3}a \,k^{3} \\ &\quad -320 A_{0}^{3} A_{1}^{3} c_{2}-160 A_{0}^{2} A_{1}^{3} c_{1} \\ &\quad -64 A_{0} A_{1}^{3} \omega , \\ 0&=-16 A_{0}^{8} c_{4}-16 A_{0}^{4} b \,k^{4}-16 A_{0}^{7} c_{3}-16 A_{0}^{4} a \,k^{3}-16 A_{0}^{6} c_{2} \\ &\quad -16 A_{0}^{5} c_{1}-16 A_{0}^{4} \omega , \\ 0&=60 A_{1} b \mu ^{4} A_{0}^{3} f g+4 A_{1}^{2} b \mu ^{4} A_{0}^{2} f^{2}-72 A_{1} b \,k^{2} \mu ^{2}A_{0}^{3} g \\ &\quad +120 A_{1}^{2} b \,k^{2} \mu ^{2} A_{0}^{2} f-448 A_{0}^{6} A_{1}^{2} c_{4} \\ &\quad -36 A_{1} a k \mu ^{2} A_{0}^{3} g+60 A_{1}^{2} a k \mu ^{2} A_{0}^{2} f-96 A_{0}^{2} A_{1}^{2} b \,k^{4}-336 A_{0}^{5} A_{1}^{2} c_{3}-96 A_{0}^{2} A_{1}^{2} a \,k^{3} \\ &\quad -240 A_{0}^{4} A_{1}^{2} c_{2}-160 A_{0}^{3} A_{1}^{2} c_{1}-96 A_{0}^{2} A_{1}^{2} \omega . \end{aligned}$$
(34)

After solving the above system of algebraic equations, we have the following set of solution

$$\begin{aligned} A_0&=0,\\ A_{1}&= \left( -\frac{105}{bc_4}\right) ^{\frac{1}{4}}\sqrt{\frac{h\Psi }{2f}}, \\ c_{1}&= \frac{g \sqrt{\Psi }\, \left( 4\Psi + \sqrt{32 b^{2} k^{4}+32 a b \,k^{3}+9 k^{2} a^{2}-4 b \omega }\right) }{\sqrt{2 f b} \left( -\frac{105 b \,h^{2}}{16 c_{4}}\right) ^{\frac{1}{4}}},\\ c_{2}&= \frac{3 \left( 13 \Psi f h-4 g^{2} \Psi -f(6 b h \,k^{2}-3 a h k)\right) }{f \sqrt{-\frac{105 b \,h^{2}}{c_{4}}}},\\ c_{3}&= -\frac{15 g h \sqrt{b\Psi }}{\sqrt{2 f} \left( -\frac{105 b \,h^{2}}{16 c_{4}}\right) ^{\frac{3}{4}}},\\ \mu&=\sqrt{\frac{2\Psi }{fb}}, \end{aligned}$$
(35)

where \(\Psi\) is defined as

$$\begin{aligned} \Psi =6 b \,k^{2}+3 a k+\sqrt{32 b^{2} k^{4}+32 a b \,k^{3}+9 k^{2} a^{2}-4 b \omega } \end{aligned}$$

and \(b,f,h,\Psi >0\) and \(c_4<0.\)

From Eq. (35) the solution of the Eq. (16) can be written as

$$\begin{aligned} U(\sigma )= \frac{2\sqrt{2fh\Psi }\left( -\frac{105}{bc_4} \right) ^{\frac{1}{4}} }{\left( g^{2}+4 f h\right) {\textrm{e}}^{\sigma \sqrt{f}}+2 g+{\textrm{e}}^{-\sigma \sqrt{f}}}. \end{aligned}$$
(36)

From the Eqs. (12), (15) and (36), the straddled soliton solution of Eq. (1) is obtained

$$\begin{aligned} q(x,t)=\left( \frac{(2)^{\frac{3}{4}}\left( fh\Psi \right) ^{\frac{1}{4}}\left( -\frac{105}{bc_4} \right) ^{\frac{1}{8}} }{\sqrt{\left( g^{2}+4 f h\right) {\textrm{e}}^{(\mu x-\lambda t) \sqrt{f}}+2 g+{\textrm{e}}^{-(\mu x-\lambda t ) \sqrt{f}}}}\right) e^{\iota (kx-\omega t+\theta )}. \end{aligned}$$
(37)

In particular if we take \(4fh=g(g-1)\) in Eq. (37), then we obtain the combination of bright-singular soliton solutions as

$$\begin{aligned} q(x,t)=\left( \frac{\sqrt{g}\left( \text{sech}\left( \frac{\mu x-\lambda t}{2}\sqrt{f}\right) \right) \left( \frac{fh\Psi }{2} \right) ^{\frac{1}{4}}\left( -\frac{105}{bc_4} \right) ^{\frac{1}{8}} }{\sqrt{g^2+fh\left( 1-\text{tanh}\left( \frac{\mu x-\lambda t}{2}\sqrt{f}\right) \right) ^2}}\right) e^{\iota (kx-\omega t+\theta )}. \end{aligned}$$
(38)

Surface plots

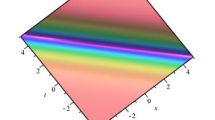
The graphical representation of solitons is an important concept in real life, especially regarding bright and dark solitons. Solitons are self-reinforcing solitary waves that maintain their shape and speed as they propagate. Bright solitons have a positive amplitude, while dark solitons have a negative amplitude. Solitons have applications in many fields, such as fiber optics, fluid dynamics, and nonlinear science. For example, bright solitons are used in optical communication systems to transmit signals over long distances without losing their shape. They are also used in studying Bose–Einstein condensates in cold atom physics. Dark solitons are important in the study of superfluids and superconductors. They are also used in the study of the propagation of light through nonlinear media. In addition, dark solitons have potential applications in developing optical switches and logic gates. Overall, the graphical presentation of solitons plays a crucial role in understanding these self-sustaining waves and their applications in various fields of science and engineering.

To better understand the behavior of the solitons generated, we can refer to Fig. 1. This figure depicts the bright solitons of solution (27) with a positive amplitude and provides a clear visualization of the dynamics under specific parameters. For instance, by selecting \(\alpha =-2,\) \(b=-0.26,\) \(\mu =-1.85,\) \(\lambda =1.8,\) and \(A_1=0.63,\) we can gain valuable insights into the characteristics of the solitons. Similarly, Fig. 2 showcases the dark soliton of solution (27) with negative amplitude, where we have chosen the same set of parameters except for \(A_1=-0.63.\) Moving on, Fig. 3 displays the bright soliton solutions (30) for the selected parameters \(\Psi =0.65,\) \(b=1.62,\) \(\mu =1.11,\) \(\lambda =0.98,\) and \(A_1=0.86,\) while Fig. 4 represents the dark soliton solutions (30) for the same parameters except for \(A_1=-0.86.\)

Conclusions

The paper is a derivation and collection of 1-soliton solutions to the NLSE that comes with 3OD and 4OD as replacements to the usual CD and the SPM structure is from cubic–quintic–septic–nonic form of nonlinear refractive index change. The retrieval of the solitons were made possible with the application of Lie symmetry analysis to the governing model that is followed by Kudryashov’s auxiliary equation approach and the hyperbolic function scheme. They collectively yielded the full spectrum of 1-soliton solutions. The study of soliton radiation has been tacitly ignored although there will be pronounced radiation in addition to the bound state and consequently soliton slow-down will be quite noticeable. The focus of this paper is on the core soliton regime.

The results of the paper are thus very promising. Next up, the model will be addressed with polarization-mode dispersion and Lie symmetry analysis will be applied there as well to recover its soliton solutions. Moving further along, the model will be addressed with dispersion-flattened fibers and the Lie symmetry analysis will be implemented to recover its soliton solutions too. The results of those research activities are currently in the bucket list and will be disseminated with time after aligning the results with the pre-existing results [51,52,53,54,55,56,57,58,59,60,61,62].