Skip to main content
SpringerLink
Log in

Non Uniform Weighted Extended B-Spline Finite Element Analysis of Non Linear Elliptic Partial Differential Equations

  • Original Research
  • Published:
Differential Equations and Dynamical Systems Aims and scope Submit manuscript

Abstract

We propose a non uniform web spline based finite element analysis for elliptic partial differential equation with the gradient type nonlinearity in their principal coefficients like p-laplacian equation and Quasi-Newtonian fluid flow equations. We discuss the well-posednes of the problems and also derive the apriori error estimates for the proposed finite element analysis and obtain convergence rate of \(\mathcal {O}(h^{\alpha })\) for \(\alpha > 0\).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Höllig, K., Reif, U., Wipper, J.: Weighted extended B-spline approximation of Dirichlet problems. SIAM J. Numer. Anal. 39, 442–462 (2001)

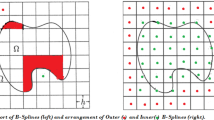
    Article  MathSciNet  Google Scholar 

  2. Höllig, K., Reif, U.: Nonuniform web-splines. Comput. Aided Geom. Des. 20, 277–294 (2003)

    Article  MathSciNet  Google Scholar 

  3. Hollig, K.: Finite element method with B-splies. Soc. Ind. Appl. Math. (2003)

  4. Chakraborty, A., Kumar, B.V.R.: Finite element method for drifted space fractional tempered diffusion equation. J. Appl. Math. Comput. 61, 117–135 (2019)

    Article  MathSciNet  Google Scholar 

  5. Chakraborty, A., Kumar, B.V.R.: Weighted extended B-spline finite element analysis of a coupled system of general elliptic equations. Int. J. Adv. Eng. Sci. Appl. Math. 10(1), 34–40 (2018)

    Article  MathSciNet  Google Scholar 

  6. Repin, S.I.: A posteriori error estimation for nonlinear variational problems by duality theory. J. Math. Sci. 99, 927–935 (2000)

    Article  MathSciNet  Google Scholar 

  7. Murthy, S.V.S.S.N.V.G.K., Kumar, B.V.R., Nigam, M.: A parallel finite element study of 3D mixed convection in a fluid saturated cubic porous enclosure under injection/suction effect. Appl. Math. Comput. 269, 841–862 (2015)

    MathSciNet  MATH  Google Scholar 

  8. Barrett, J.W., Liu, W.B.: Quasi-norm error bounds for the finite element approximation of a non-Newtonian flow. Numerische Mathematik 68(4), 437–456 (1994)

    Article  MathSciNet  Google Scholar 

  9. Melenk, J.M., Babuška, I.: The partition of unity finite element method: basic theory and applications. Comput. Methods Appl. Mech. Eng. 139, 289–314 (1996)

    Article  MathSciNet  Google Scholar 

  10. Arbogast, T.: The existence of weak solutions to single porosity and simple dual-porosity models of two-phase incompressible flow. Nonlinear Anal. 19, 1009–1031 (1992)

    Article  MathSciNet  Google Scholar 

  11. Kumar, S.: A new analytical modelling for fractional telegraph equation via Laplace transform. Appl. Math. Modell. 38(13), 3154–3163 (2014a)

    Article  MathSciNet  Google Scholar 

  12. Kumar, S., Mohammad, M.R.: New analytical method for gas dynamics equation arising in shock fronts. Comput. Phys. Commun. 185(7), 1947–1954 (2014)

    Article  MathSciNet  Google Scholar 

  13. Kumar, S.: A new efficient algorithm to solve non-linear fractional Ito coupled system and its approximate solution. Walailak J. Sci. Technol. (WJST) 11(12), 1057–1067 (2014)

    Google Scholar 

  14. Kumar, S.: A new mathematical model for nonlinear wave in a hyperelastic rod and its analytic approximate solution. Walailak J. Sci. Technol. (WJST) 11(11), 965–973 (2014)

    Google Scholar 

  15. Zienkiewicz, O.C., Taylor, R.L.: The Finite Element Method: Solid Mechanics, vol. 2. Butterworth-heinemann, Oxford (2000)

    MATH  Google Scholar 

  16. Chaudhary, S., Kumar, V.V.K.: Web-spline-based finite element approximation of some quasi? Newtonian flows: existence? Uniqueness and error bound. Numer Methods Part. Differ. Equ. (2015). https://doi.org/10.1002/num.21894

    Article  MathSciNet  MATH  Google Scholar 

  17. Boor, De, Carl, Höllig K., Riemenschneider, S.: Box Splines. Springer, Berlin (2013)

    MATH  Google Scholar 

  18. de Boor, C.: Cardinal Splines, IJ Schoenberg Selected Papers. Birkhauser, Boston, pp. 164–166 (1988)

  19. Rvachev, V.L., Sheiko, T.I.: R-functions in boundary value problems in mechanics. Appl. Mech. Rev. 48(4), 151–188 (1995)

    Article  Google Scholar 

  20. Barrett, J.W., Liu, W.B.: Finite element approximation of the p-Laplacian. Math. Comput. 61(204), 523–537 (1993)

    MathSciNet  MATH  Google Scholar 

  21. Glowinski, R., Marroco, A.: Sur l’approximation, par éléments finis d’ordre un, et la résolution, par pénalisation-dualité d’une classe de problèmes de Dirichlet non linéaires”. Revue française d’automatique, informatique, recherche opérationnelle. Anal. Numérique 9(2), 41–76 (1975)

    Article  MathSciNet  Google Scholar 

  22. Chow, S.S.: Finite element error estimates for non-linear elliptic equations of monotone type. Numerische Mathematik 54(4), 373–393 (1989)

    Article  MathSciNet  Google Scholar 

  23. Tyukhtin, V.B.: The rate of convergence of approximation methods of solution of one-sided variational problems. Izv. Leningr. Univ. Mat. Mekh. Astronom. 13, 111–113 (1982)

    MathSciNet  MATH  Google Scholar 

  24. Raviart, P.-A., Thomas, J.-M.: A Mixed Finite Element Method for 2-nd Order EElliptic Problems. Mathematical Aspects of Finite Element Methods, pp. 292–315. Springer, Berlin (1977)

    Google Scholar 

  25. Baranger, J., Najib, K., Sandri, D.: Numerical analysis of a three-fields model for a quasi-Newtonian flow. Comput. Methods Appl. Mech. Eng. 109, 281–292 (1993)

    Article  MathSciNet  Google Scholar 

  26. Liu, W.B., Barrett, J.W.: Quasi-norm error bounds for the finite element approximation of some degenerate quasilinear elliptic equations and variational inequalities. ESAIM 28(6), 725–744 (1994)

    Article  MathSciNet  Google Scholar 

  27. Amrouche, C., Girault, V.: Giroire J (1994) Weighted Sobolev spaces for Laplace’s equation in Rn. J. Mathématiques Pures et Appliquées 73(6), 579–606 (1994)

    MathSciNet  MATH  Google Scholar 

  28. Barrett, J.W., Liu, W.B.: Finite element error analysis of a quasi-Newtonian flow obeying the Carreau or power law. Numerische Mathematik 64(1), 433–453 (1993)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors are grateful to the reviewers for their careful reading and intuitive implications.

Author information

Authors and Affiliations

  1. IIT Kanpur, Kanpur, India

    Ayan Chakraborty

  2. Department of Mathematics and Statistics, Indian Institute of Technology Kanpur, Kanpur, India

    B. V. Rathish Kumar

Authors
  1. Ayan Chakraborty
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. B. V. Rathish Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to B. V. Rathish Kumar.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chakraborty, A., Kumar, B.V.R. Non Uniform Weighted Extended B-Spline Finite Element Analysis of Non Linear Elliptic Partial Differential Equations. Differ Equ Dyn Syst 30, 485–497 (2022). https://doi.org/10.1007/s12591-020-00557-1

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12591-020-00557-1

Keywords

Search

Navigation