1 Introduction

The long range dependence phenomena, called also long memory or the Joseph effect, first was introduced by Mandelbrot and Wallis in 1968 [1]. Since that time the models and processes which exhibit long memory property have found many applications and number of research papers devoted to this phenomenon increased rapidly. The long range dependence we observe in many real data, we only mention here economic and financial applications [2, 3], physics and natural sciences [4, 5], as well as hydrology, meteorology and geophysics [6,7,8,9]. In [10], one can find the additional interesting examples of long range dependent time series, like single particle tracking dynamics in molecular biology, electromagnetic field data or high solar flare activity.

The long range dependence relates to the rate of decay of statistical dependence of two points with increasing time interval or spatial distance between the points. A phenomenon is usually considered to have long range dependence if the dependence decays more slowly than an exponential decay, typically a power-like decay. The classic examples of long range dependent processes are Gaussian fractional integrated autoregressive moving average (FARIMA or ARFIMA) time series [5] and increments of fractional Brownian motion (FBM) [6], which is closely related to fractional Langevin equation motion [11] and is a generalization of the classic Brownian motion. One way of characterizing long- and short-range dependence of second order processes is in terms of their autocovariance functions. For short-range dependent processes, the relation between values at different times decreases rapidly as the time difference increases. Either the autocovariance drops to zero after a certain time lag, or it eventually has an exponential decay. For processes with long range dependence, there is much stronger relation. It is worth mentioning that the slowly decaying autocovariance function is typical for processes with long range dependence; however, we observe the same effect for continuous time random walk (CTRW) [12], which has no long memory property [13].

One of the extensions of the FBM is the fractional \(\alpha \)-stable motion (FLSM), which is constructed in analogy to the relation between Brownian motion and its generalization, \(\alpha \)-stable motion [14]. The FLSM is \(\alpha \)-stable distributed and, similarly to the FBM, it exhibits a long memory property. Due to the fact that a second moment of the process does not exist, the long range dependence in this case cannot be expressed in the language of autocovariance function but by means of dependence measures adequate for the \(\alpha \)-stable distribution [15]. The another example of processes with long memory which cannot be expressed by means of autocovariance function is the \(\alpha -\)stable FARIMA time series [3, 5, 16,17,18,19].

The alternative measures of dependence adequate for infinite variance processes are rarely discussed in the literature. The classic covariance or autocovariance used in correlation analysis, can be generalized for the \(\alpha \)-stable process, leading to the notion of covariation [20, 21]. Its definition is based on the spectral measure of given process [22, 23]. The other alternative measure is the L\(\acute{e}\)vy correlation cascade [24]. In contrast to the covariation which is defined only for processes based on symmetric \(\alpha -\)stable distribution, it is defined for general class of infinitely divisible processes [15, 25]. This measure can be considered, similar as autocovariance in Gaussian case, as a tool of long range dependence recognition. Moreover, it is also an useful tool in the problem of mixing property testing [15]. However, the most commonly used measure of dependence which can be an alternative for autocovariance is the codifference. Its definition is based on the characteristic function of a given process, therefore it can be used not only for \(\alpha \)-stable processes. Moreover, the codifference in the Gaussian case reduces to the classic covariance, so it can be treated as the natural extension of the well-known measure. On the other hand, according to the definition, it is easy to evaluate the empirical codifference which is based on the empirical characteristic function of the analyzed data. It is worth to mention that the codifference is closely related to the so-called dynamical functional used to study ergodic properties of stochastic processes [20, 23, 26,27,28]. In the literature, the codifference very often is considered also as a measure on the basis of which it is possible to recognize the long memory property of given process [15].

In this paper, we study the structure of dependence for two Ornstein-Uhlenbeck models based on long memory processes. Their are extensions of the Ornstein-Uhlenbeck system for which in the classic version we replace the standard Brownian motion (or other L\(\acute{e}\)vy process) by long range dependent processes based on \(\alpha -\)stable distribution. The Ornstein-Uhlenbeck process is one of the famous examples of continuous time models. This process was originally introduced by Uhlenbeck and Ornstein [29] as a suitable model for the velocity process in the Brownian diffusion. In other words, this process provides a stationary solution for the classic Klein-Kramers dynamics, [30, 31]. The Ornstein-Uhlenbeck process has been of fundamental importance for theoretical studies in physics and mathematics, but it has also been used in many applications including financial data such as interest rates, currency exchange rates and commodity prices. In finance, it is best known in connection with the Vasiček interest rate model, [32], which was one of the earliest stochastic models of the term structure. The model exhibits mean reversion, which means that if the interest rate is above the long run mean, then the drift becomes negative so that the rate will be pushed down to be closer to the mean level. Likewise, if the rate is below the long run mean, then the drift remains positive so that the rate will be pushed up to the mean level. Such mean reversion feature complies with the economic phenomenon that in the long time period interest rates appear to be pulled back to some average value [33].

In the literature, one can find many different extensions of the classic Ornstein-Uhlenbeck process. One of the possibility is to replace the Brownian motion by another L\(\acute{e}\)vy process [25, 34, 35]. The second possibility is to replace the time in the Ornstein-Uhlenbeck process by another process, called subordinator (or inverse subordinator) [28, 33, 36]. As it was mentioned earlier, in this paper we also extend the classic definition of the Ornstein-Uhlenbeck process. We analyse two different processes based on the Ornstein-Uhlenbeck system in the language of their measures of dependence adequate for processes with infinite variance. The similar problem was considered for example in [15] and [37]. We check if the analyzed processes exhibit long memory behavior expressed by means of alternative measures of dependence. Moreover, we show their are mixing. At the end, we demonstrate that for analyzed cases the ratio of two considered measures of dependence is limited. The similar, but more strong result, we obtained for Ornstein-Uhlenbeck process based on \(\alpha -\)stable L\(\acute{e}\)vy motion [38].

The rest of the paper is organized as follows: in sect. 2, we introduce the classic Ornstein-Uhlenbeck process and its extensions based on the long memory processes and \(\alpha -\)stable distribution. Next, in sect. 3 we discuss the problem of structure of dependence for processes with infinite variance. We present here three measures, namely covariation, codifference and L\(\acute{e}\)vy correlation cascade which can be considered as the alternative measures. Moreover, we indicate how those measures can be helpful in the problem of long range dependence testing. In sect. 4, we consider separately two Ornstein-Uhlenbeck processes in the context of their measures of dependence expressed in the language of mentioned measures. We check if the analyzed systems exhibit long range dependence and indicate mixing property. Moreover, we analyse the ratio between codifference and covariation and show it is limited. Last section concludes the paper.

2 The Ornstein-Uhlenbeck model based on long memory processes

2.1 The Ornstein-Uhlenbeck model driven by L\(\acute{e}\)vy processes

The classic stationary Ornstein-Uhlenbeck process can be obtained in two different ways. On the one hand, it is a stationary solution of a Langevin equation with a Brownian motion noise. On the other hand, it can be obtained from a Brownian motion by the so-called Lamperti transformation, [39]. The classic Ornstein-Uhlenbeck process \(\{X(t)\}\) is a solution of a stochastic differential equation given by the following equation, [29]:

$$\begin{aligned} dX(t)+aX(t))dt=bdB(t), \end{aligned}$$
(1)

where \(a> 0\) and \(b > 0\) are the model parameters, and \(\{B(t)\}\) denotes the Brownian motion.

In economics, this process is called the Vasiček model [32] and is the most classic approach to modeling interest rates, currency exchange rates and commodity prices. The popularity of that model comes from its mean-reverting feature, meaning that in a long time period the process will go back to its equilibrium level (in our case zero). If the process is below the (long-term) mean, the drift will be positive, pulling the process up to the equilibrium level. Analogously, if the process is above the mean, the drift will be negative, pulling the process down to the equilibrium level. The parameter a is responsible for the speed of mean-reversion while b denotes the volatility. In physical sciences, the Ornstein-Uhlenbeck process is a prototype of a noisy relaxation process, whose probability density function (pdf) f(x, t) can be described by the Fokker-Planck equation, [33, 40,41,42,43,44]:

$$\begin{aligned} \frac{\partial f(x,t)}{\partial t}=\frac{\partial }{\partial x}[axf(x,t)] +\frac{b^2}{2}\frac{\partial ^2f(x,t)}{\partial x^2}. \end{aligned}$$
(2)

It is worth mentioning the Ornstein-Uhlenbeck process defined as in (1) is a special case of the so-called CARMA process (continuous time autoregressive process) [34]. The classic version of Ornstein-Uhlenbeck process can be extended to more general class, namely we can consider the Ornstein-Uhlenbeck process driven by L\(\acute{e}\)vy process (i.e., process with stationary independent increments) [34]:

$$\begin{aligned} dX(t)+aX(t))dt=bdL(t), \end{aligned}$$
(3)

where \(\{L(t)\}\) is a general L\(\acute{e}\)vy process. If we extend the process \(\{L(t)\}\) in equation (3) for the set \((-\infty , 0)\) then the unique stationary solution of 3 is given by [34]:

$$\begin{aligned} X(t)=\int _{-\infty }^{t}be^{-a(t-u)}dL(u). \end{aligned}$$
(4)

The process defined in (3) and its generalization, namely CARMA system driven by general L\(\acute{e}\)vy process, was considered for different \(\{L(t)\}\) processes. However, the special importance have here Brownian motion and \(\alpha -\)stable L\(\acute{e}\)vy process [28, 35, 38, 45,46,47,48,49,50]. We should also mention, system 4 was considered also in case of tempered stable process [25] as well as process based on variance gamma distribution [35]. The other examples of L\(\acute{e}\)vy processes in definition 3 one can find for example in [45].

2.2 The Ornstein-Uhlenbeck model based on long memory processes

In this paper, we study two types of the Ornstein-Uhlenbeck model based on long memory processes. The long memory issue is discussed in the next sections. The first considered process \(\{Y(t)\}\) is defined via the the Langevin equation in the following way [37]:

$$\begin{aligned} dY(t)+aY(t)dt=bdL_{\alpha ,H}(t), ~0<\alpha \le 2,~0<H<1, \end{aligned}$$
(5)

where \(\{L_{\alpha ,H}(t), ~t\in {\mathbb {R}}\}\) is a fractional stable motion defined as follows:

$$\begin{aligned} L_{\alpha ,H}(t)=\int _{-\infty }^{\infty }(t-x)_{+}^{H-1/\alpha } -(-x)_{+}^{H-1/\alpha }dZ_{\alpha }(x), \end{aligned}$$
(6)

where \(\{Z_{\alpha }(x)\}\) denotes a two-sided symmetric \(\alpha -\)stable L\(\acute{e}\)vy process with \(\mathrm{E}[e^{i\theta Z_{\alpha }(1)}]=e^{-|\theta |^{\alpha }}\) and \(u_{+}=\max (u,0)\), \(u_{-}=\max (-u,0)\).

The process given in (5) is a natural extension of the Ornstein-Uhlenbeck model driven by L\(\acute{e}\)vy process defined in (3). It is also an extension of presented in [51] CAR(1) process with symmetric \(\alpha -\)stable L\(\acute{e}\)vy motion discussed in the context of the asymptotic behavior of the corresponding measures of dependence.

Recall that we are restricting ourselves to the case \(1/\alpha<H<1\) and \(1<\alpha <2\).

Using results presented in [37] (Theorem 4.1), we obtain the following form of the unique stationary solution of equation (5) under the assumption \(a>0\):

$$\begin{aligned} Y(t)=\int _{-\infty }^t\beta b\int _{x}^te^{-a(t-u)}(u-x)^{\beta -1}dudZ_{\alpha }(x), \end{aligned}$$
(7)

where \(\beta =H-1/\alpha \). Equation (7) can be written in the equivalent form:

$$\begin{aligned} Y(t)= & {} \int _{-\infty }^tf(t-x)dZ_{\alpha }(x),~\text{ for }~ f(y)\nonumber \\= & {} \beta b\int _{0}^{y}e^{-a(y-u)}u^{\beta -1}du. \end{aligned}$$
(8)

As the second Ornstein-Uhlenbeck model based on long memory process, we consider some modification of the fractional stable noise used in 5, namely we analyse the process \(\{Y^{*}(t)\}\) given by:

$$\begin{aligned} dY^{*}(t)+aY^{*}(t)dt=bdL^{*}_{\alpha ,\kappa }(t) \end{aligned}$$
(9)

with the noise term given by:

$$\begin{aligned} L^{*}_{\alpha ,\kappa }(t)=\frac{1}{\varGamma (\kappa )}\int _{-\infty }^{t} \left( t-x+1\right) ^{\kappa -1}dZ_{\alpha }(x),\quad t\in {\mathbb {R}}. \end{aligned}$$
(10)

In the above equation, similar as in the previous case, \(\{Z_{\alpha }(x)\}\) denotes a two-sided symmetric \(\alpha -\)stable L\(\acute{e}\)vy process, and \(\varGamma \) is the gamma function.

The process \(\{Y^{*}(t)\}\) is stationary since it is a moving average process, moreover it is well defined when \(\kappa <1-1/\alpha \). Since its dependence structure is similar to FARIMA time series it is also called the continuous time FARIMA process [15].

Again using the results presented in [37], we obtain the following form of unique stationary solution of 9:

$$\begin{aligned} Y^{*}(t)&=\frac{b}{\varGamma (\kappa )}\int \limits _{-\infty }^{t}\nonumber \\&\quad \left( (\kappa -1)\int _s^t (u-s+1)^{\kappa -2}\right. \nonumber \\&\qquad \quad \left. e^{-a(t-u)}\,du +e^{-a(t-s)} \right) Z_{\alpha }(ds). \end{aligned}$$
(11)

In order to explain why we could write such an equation, one needs to notice that we followed Proposition 2.1 from [37], which is based on important result from [52]. In this case, we have to clarify two issues. First, we do not need to assume that \(L^{*}_{\alpha ,\kappa }(t)=0\) a.s. since this is not crucial assumption in the proof of the mentioned theorem, and clearly this assumption is not satisfied for the process given in 11. Secondly, since our process is obviously \(\alpha \)-stable in order to prove first condition of Proposition 2.1 in [37] one can for instance use Theorem 11.3.2 from [20]. The other conditions are proved in [37].

One can see the equivalent form of equation (11) is as follows:

$$\begin{aligned} Y^{*}(t)&=\int \limits _{-\infty }^{t}f(t-s)Z_{\alpha }(ds), ~~\text{ for }~~f(y)\nonumber \\&=\frac{b(\kappa -1)}{\varGamma (\kappa )}\int _0^y (u+1)^{\kappa -2}e^{-a(y-u)}\,du +\frac{b}{\varGamma (\kappa )}e^{-ay}. \end{aligned}$$
(12)

In the further analysis, we will call the process \(\{Y(t)\}\) as the 1st type of the Ornstein-Uhlenbeck model based on long memory process while the process \(\{Y^{*}(t)\}\) as the 2nd type.

The introduced above Ornstein-Uhlenbeck processes have infinite variances, therefore their structures of dependence cannot be described in the language of the classic measures of dependence, namely autocovariance (or autocorrelation). In the next sections, we will analyse introduced modifications of the Ornstein-Uhlenbeck processes in the context of their measures of dependence adequate for systems with infinite variance. However, first the general idea of alternative measures of dependence for processes with infinite variance will be introduced.

3 Measures of dependence for processes with infinite variance

For the processes for which the second moment does not exist the classic measure as autocovariance (or autocorrelation) cannot be considered as a tool for measuring interdependence of the process. Thus, other measures of dependence have to be used. Becuase in this paper we concentrate only on the processes based on the \(\alpha -\)stable L\(\acute{e}\)vy motion of the form:

$$\begin{aligned} X(t)=\int \limits _{-\infty }^{t}f(t-s)Z_{\alpha }(ds), \end{aligned}$$
(13)

where \(f(\cdot )\) is a deterministic function, and \(\{Z_{\alpha }(s)\}\) is two-sided symmetric \(\alpha -\)stable L\(\acute{e}\)vy process with \(\mathrm{E}[e^{i\theta Z_{\alpha }(1)}]=e^{-|\theta |^{\alpha }}\) ,therefore the formulas of alternative measures of dependence introduced in this section we show for the processes given by (13). As it was mentioned earlier, we restrict ourselves to the case \(1<\alpha \le 2\).

One of the measure that is often considered as a tool for measuring interdependence is the codifference. For the stationary infinite divisible process \(\{X(t)\}\) , the codifference is defined as follows [20]:

$$\begin{aligned}&CD(X(t),X(0))\nonumber \\&\quad =\log (\mathrm{E}\exp (i(X(t)-X(0)))-\log (\mathrm{E}\exp (iX(t)))\nonumber \\&\qquad -\log (\mathrm{E}\exp (-iX(0))). \end{aligned}$$
(14)

The main properties of the codifference one can find for example in [20], we only mention here, this measure can be considered as an extension of the autocovariance. This is related to the fact that in case the \(\{X(t)\}\) process is Gaussian that the codifference reduces simply to the autocovariance [23]. It is worth to mention, the codifference carries enough information to detect ergodic properties of the process \(\{X(t)\}\) [15]. It is also closely related to another measure, namely dynamical functional, discussed for example in [10, 26, 27, 53,54,55] in the context of chaotic behavior of considered process. The codifference is also used to examine the so-called long range dependence (or long memory) in case when the correlation function is not defined [17]. We remind the reader the long-range dependency, also called long memory or long-range persistence, is a phenomenon that may arise in the analysis of spatial or time series data. It relates to the rate of decay of statistical dependence of two points with increasing time interval or spatial distance between the points. A phenomenon is usually considered to have long-range dependence if the dependence decays more slowly than an exponential decay, typically a power-like decay. One way of characterising long range and short range dependent stationary process is in terms of their autocovariance function. However, when we consider the process for which the second moment does not exist the long range dependence can be expressed in the language of alternative measures, like codifference. The stationary process \(\{X(t)\}\) is said to have a long memory in terms of the codifference function if the following condition holds:

$$\begin{aligned} \sum _{n=0}^{\infty }|CD(Y(n),Y(0))|=\infty . \end{aligned}$$
(15)

At the end we should mention, for the real data the codifference can be estimated on the basis of the empirical characteristic function [56,57,58]. The estimator of codifference for linear \(\alpha -\)stable process has very good properties and can be successfully used for instance in the problem of proper model recognition [23] as well as to detect impulsive behavior of real data [59].

Another alternative measure of dependence is the covariation. This measure is defined only for symmetric \(\alpha -\)stable random variables with \(\alpha >1\). If \(T_1\) and \(T_2\) are jointly symmetric \(\alpha -\)stable with \(\alpha >1\) , and \(\varGamma \) is the spectral measure of a random vector \((T_1,T_2)\), then the covariation of \(T_1\) on \(T_2\) is the real number defined as [20]:

$$\begin{aligned} CV(T_1,T_2)=\int _{S_2}s_1s_2^{<\alpha -1>}\varGamma (ds), \end{aligned}$$
(16)

where \(S_2\) is the unit sphere in \({\mathbb {R}}^2\) , and the signed power \(z^{<p>}\) is given by \(z^{<p>}=|z|^{p}sign(z)\). The main properties of the covariation one can find in [20]. We only mention, in contrast to codifference, the covariation is not symmetric measure and when \(\alpha =2\) it is equal to half of the covariance of \(T_1\) on \(T_2\). Moreover, for \(\alpha >1\), the covariation induces a norm on the linear space of jointly symmetric \(\alpha -\)stable random variables. Namely, if \(T_1\) is a symmetric \(\alpha -\)stable random variable with \(\alpha >1\), then:

$$\begin{aligned} ||T_1||_{\alpha }=(CV(T_1,T_1))^{1/\alpha }. \end{aligned}$$

The covariation norm of given random variable is equal to its scale parameter, denoted as \(\sigma \). If we assume \(T_1\) and \(T_2\) are symmetric \(\alpha -\)stable with \(\alpha >1\), then the codifference of \(T_1\) on \(T_2\) can be expressed in the language of the covariation norm, namely [20, 22]:

$$\begin{aligned} CD(T_1,T_2)=||T_1||_{\alpha }^{\alpha }+||T_2||_{\alpha }-||T_1-T_2||_{\alpha }^{\alpha }. \end{aligned}$$
(17)

For the process \(\{X(t)\}\) given by formula (13), the covariation takes the form (see Proposition 3.5.2 in [20]):

$$\begin{aligned} CV(Y(t),Y(0))&=\int _{-\infty }^{\min (t,0)}f(t-x)f(-x)^{<\alpha -1>}dx, \end{aligned}$$
(18)
$$\begin{aligned} CV(Y(0),Y(t))&=\int _{-\infty }^{\min (t,0)}f(-x)f(t-x)^{<\alpha -1>}dx, \end{aligned}$$
(19)

Moreover from the relation between the covariation and codifference for \(\alpha >1\) given in (17), we obtain:

$$\begin{aligned}&CD(Y(t),Y(0))\nonumber \\&\quad =\int _{-\infty }^{\min (t,0)}|f(t-x)|^{\alpha } +|f(-x)|^{\alpha }-|f(t-x)-f(-x)|^{\alpha }dx. \end{aligned}$$
(20)

The last considered measure of dependence is defined, similar as the codifference, for infinitely divisible stochastic processes \(\{X(t)\}\) with the following integral representation [15, 25]:

$$\begin{aligned} X(t)=\int _{X}K(t,x)M(dx), \end{aligned}$$
(21)

where M is an independently scattered infinitely divisible random measure on some measurable space with control measure m.

The measure was introduced in [24] as a new concept of correlation cascades, which is a promising tool for exploring the properties of the Poissonian part of X(t) and the dependence structure of this stochastic process. The L\(\acute{e}\)vy correlation cascade is defined as follows [15]:

$$\begin{aligned} C_l(t_1,t_2,\dots ,t_n)=\int _{X}\varLambda \left( \frac{l}{\min \{K(t_1,x),\dots ,K(t_n,x)\}}\right) m(dx), \end{aligned}$$
(22)

where the tail function \(\varLambda \) is given by:

$$\begin{aligned} \varLambda (l)=\int _{|x|>l}v(dx) \end{aligned}$$

and v is a L\(\acute{e}\)vy measure of the process \(\{X(t)\}\).

In the simple symmetric \(\alpha -\)stable case, the tail function \(\varLambda \) takes the simple form:

$$\begin{aligned} \varLambda (l)=\frac{2}{\alpha }l^{-\alpha } \end{aligned}$$
(23)

and for the process \(\{X(t)\}\) with the integral representation (13) and the control Lebesgue measure, the L\(\acute{e}\)vy correlation cascade \(C_l\) of X(t) on X(0) has the form:

$$\begin{aligned} C_{l}(t,0)=\frac{2}{\alpha } l^{-\alpha }\int \limits _{t}^{\infty }|f(x)|^{\alpha }dx. \end{aligned}$$
(24)

The L\(\acute{e}\)vy correlation cascade can be useful in the problem of long memory testing for processes with infinite variance. We say the stationary process \(\{X(t)\}\) has a long memory in terms of the L\(\acute{e}\)vy correlation cascade if the following condition holds [15]:

$$\begin{aligned} \sum _{n=0}^{\infty }r(n,0)=\infty , \end{aligned}$$
(25)

where the function \(r(n,0)=C_l(n,0)/C_l(0,0)\) is considered as correlation-like measure of dependence.

It should be also mentioned the L\(\acute{e}\)vy correlation cascade is a tool for testing if given process is mixing. The basic concept of mixing the reader can find in the fundamental paper by [60]. The stationary infinitely divisible process \(\{X(t)\}\) given in (21) is mixing iff [15]:

$$\begin{aligned} \lim _{t\rightarrow \infty }C_l(t,0)=0 \end{aligned}$$

for every \(l>0\).

It is worth to mention, there is relationship between asymptotic behaviour of L\(\acute{e}\)vy correlation cascade and the codifference, namely for the stationary infinite divisible process \(\{X(t)\}\) with the L\(\acute{e}\)vy measure \(v_0\) of X(0) without atoms in \(2\pi Z\) the following conditions are equivalent [15]:

$$\begin{aligned}&\lim _{t\rightarrow \infty }C_l(t,0)=0,~~\text{ for } \text{ every }~~l>0,\\&\lim _{t\rightarrow \infty }CD(X(t),X(0))=0. \end{aligned}$$

4 Asymptotic behavior of the measures of dependence for the Ornstein-Uhlenbeck model based on long memory processes

In this section, we prove important properties of analyzed Ornstein-Uhlenbeck processes introduced in sect. 2. Those properties are related to the structure of dependence for examined systems expressed in the language of measures of dependence adequate for processes with infinite variance. We analyse separately the 1st type of the Ornstein-Uhlenbeck model based on long memory process and the 2nd type. At the end of each subsection, we check if the analyzed process exhibits properties adequate to long memory behavior, expressed in the language of mentioned measures of dependence.

4.1 The 1st type of the Ornstein-Uhlenbeck model based on long memory process

Theorem 4.11

[37] If \(\{Y(t)\}\) is a solution of equation (5), then the codifference of Y(t) on Y(0) satisfies:

$$\begin{aligned} CD(Y(t),Y(0))=k(\alpha ,H)|t|^{\alpha (H-1)},~\text{ as }~t\rightarrow -\infty , \end{aligned}$$

where

$$\begin{aligned} k(\alpha ,H)= & {} a^{-\alpha }(b(H-1/\alpha ))^{\alpha }\\&\left[ \int _{1}^{\infty }\left| (x-1)^{H-1/\alpha -1}\right| ^{\alpha } +\left| x^{H-1/\alpha -1}\right| ^{\alpha }\right. \\&\qquad \left. -\left| (x-1)^{H-1/\alpha -1}-x^{H-1/\alpha -1}\right| ^{\alpha }\right] dx. \end{aligned}$$

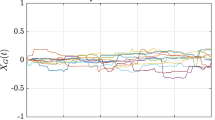
In Fig. 1, we present empirical CD together with its theoretical asymptotics as predicted in Theorem 4.11.

Fig. 1
figure 1

Comparison between empirical CD and theoretical CD for the 1st type of the Ornstein-Uhlenbeck process. One can observe almost perfeect agreement (notice the scale on the Y axis) between empirical CD and theoretical one derived in Theorem 4.11. Parameters are: \(H=0.5,\,\alpha =1.8.\). Here values on the X axis are negative

Full size image

Theorem 4.12

If \(\{Y(t)\}\) is a solution of equation (5), then the covariation of Y(t) on Y(0) fulfills:

$$\begin{aligned} CV(Y(t),Y(0))= c_1(\alpha ,H)|t|^{\alpha (H-1)}~\text{ as }~t\rightarrow -\infty . \end{aligned}$$

where

$$\begin{aligned} c_1(\alpha ,H)= & {} a^{-\alpha }(b(H-1/\alpha ))^{\alpha }\nonumber \\&\int _{1}^{\infty }(x-1)^{(H-1/\alpha -1)(\alpha -1)}x^{(H-1/\alpha -1)}dx, \end{aligned}$$

Proof

Using (18), (19) and the form of the solution of equation (5), we obtain:

$$\begin{aligned}&CV(Y(t),Y(0))\\&\quad =(\beta b)^{\alpha }\int _{-\infty }^t \left( \int _x^te^{-a(t-u)}(u-x)^{\beta -1}du\right) \\&\qquad \left( \int _x^0e^{au}(u-x)^{\beta -1}du\right) ^{<\alpha -1>}dx. \end{aligned}$$

Here by change of variables \(x=xt\) and \(u=ut\), we have:

$$\begin{aligned} CV(Y(t),Y(0))= & {} (\beta b)^{\alpha }|t|^{\alpha (H-1)}\\&\quad \int _{1}^{\infty }\left( \int _1^xte^{at(u-1)}(x-u)^{\beta -1}du\right) \\&\qquad \left( \int _0^xte^{atu}(x-u)^{\beta -1}du\right) ^{<\alpha -1>}dx. \end{aligned}$$

Using Lemma 5.4 in [37], i.e.,

$$\begin{aligned}&\lim _{t\rightarrow -\infty }\int _1^xte^{at(u-1)}(x-u)^{\beta -1}du =\frac{1}{a}(x-1)^{\beta -1},\\&\lim _{t\rightarrow -\infty }\int _0^xte^{atu}(x-u)^{\beta -1}du =\frac{1}{a}x^{\beta -1}, \end{aligned}$$

we obtain:

$$\begin{aligned} \lim _{t\rightarrow -\infty }|t|^{\alpha (1-H)}CV(Y(t),Y(0))=c_1(\alpha ,H). \end{aligned}$$

\(\square \)

Theorem 4.13

If the process \(\{Y(t)\}\) is a solution of equation (5), then the L\(\acute{e}\)vy correlation cascade \(C_l(0,t)\) of Y(t) on Y(0) satisfies:

$$\begin{aligned} C_l(0,t)=l^{-\alpha }q(\alpha ,H)|t|^{\alpha (H-1)},~\text{ as }~t\rightarrow \infty , \end{aligned}$$

where

$$\begin{aligned} q(\alpha ,H)=\frac{4|b\beta |^{\alpha }}{a^{\alpha }\alpha ^2(1-H)}. \end{aligned}$$

Proof

Using (24) and (8) for \(t>0\) , we obtain:

$$\begin{aligned} C_l(0,t)= & {} \frac{2|\beta b|^{\alpha }}{l^{\alpha }\alpha } \int _{t}^{\infty }\left| \int _{0}^xe^{-a(x-u)}u^{\beta -1}du\right| ^{\alpha }dx\\= & {} \frac{2|\beta b|^{\alpha }}{l^{\alpha }\alpha }\int _{t}^{\infty } \left| \int _{-x}^0e^{au}(u+x)^{\beta -1}du\right| ^{\alpha }dx. \end{aligned}$$

By change the variables \(x=xt\), \(u=ut\), we have:

$$\begin{aligned} C_l(0,t)= & {} \frac{2|\beta b|^{\alpha }}{l^{\alpha }\alpha }|t|^{\alpha (H-1)}\\&\int _1^{\infty }\left| \int _{-x}^0te^{atu}(u+x)^{\beta -1}du\right| ^{\alpha }dx. \end{aligned}$$

Let us denote

$$\begin{aligned}&f_1:=\lim _{t\rightarrow \infty }\int _{-x}^0te^{atu}(u+x)^{\beta -1}du=f_2+f_3,\\&f_2:=\lim _{t\rightarrow \infty }\int _{-x}^{\frac{-x+1}{2}}te^{atu}(u+x)^{\beta -1}du,\\&f_3:=\lim _{t\rightarrow \infty }\int _{\frac{-x+1}{2}}^{0}te^{atu}(u+x)^{\beta -1}du. \end{aligned}$$

Then we obtain:

$$\begin{aligned} f_3= & {} \lim _{t\rightarrow \infty }\int _{\frac{(-x+1)t}{2}}^{0}e^{au} \left( \frac{u}{t}+x\right) ^{\beta -1}du\\= & {} \lim _{t\rightarrow \infty }\int _{-\infty }^{0} I_{\left\{ \frac{t(1-x)}{2}<u<0\right\} }e^{au}\left( \frac{u}{t}+x\right) ^{\beta -1}du, \end{aligned}$$

where

$$\begin{aligned}&I_{\left\{ \frac{t(1-x)}{2}<u<0\right\} }e^{au}\left( \frac{u}{t}+x\right) ^{\beta -1}\\&\quad \le e^{au}\left( \frac{x}{2}+\frac{1}{2}\right) ^{\beta -1}, \end{aligned}$$

which is integrable with respect to u over \((-\infty ,0)\). Hence, by dominated convergence theorem we obtain:

$$\begin{aligned} f_3=\lim _{t\rightarrow \infty }\int _{-\infty }^0e^{au}x^{\beta -1}du =\frac{\left( x+1\right) ^{\beta -1}}{a2^{\beta -1}}. \end{aligned}$$

Moreover

$$\begin{aligned} |f_2|\le |t|e^{at\frac{1-x}{2}}\int _{-x}^{\frac{-x+1}{2}}(u+x)^{\beta -1}du=0. \end{aligned}$$

Therefore, we obtain:

$$\begin{aligned}&\lim _{t\rightarrow \infty }C_l(0,t)|t|^{\alpha (1-H)}\\&\quad =\frac{2|\beta b|^{\alpha }}{(al)^{\alpha }\alpha 2^{\alpha (\beta -1)}} \int _1^{\infty }\left( x+1\right) ^{\alpha (\beta -1)}dx=l^{-\alpha }q(\alpha ,H). \end{aligned}$$

\(\square \)

In the next corollary, we formulate simple fact concerning mixing property of the investigated process.

Corollary 4.11

If the process \(\{Y(t)\}\) is a solution of equation (5) then it is mixing.

Proof

Proof of this theorem follows from Theorem 1 in [15].

Moreover, one can also state an important result about the long memory property of the 1st type of the Ornstein-Uhlenbeck model based on long memory process defined in equation (5). Since in the sense of codifference or L\(\acute{e}\)vy correlation cascade we have that both of these measures of dependence decay proportionally to \(|t|^{\alpha (H-1)}\) we also have the following corollary. \(\square \)

Corollary 4.12

If the process \(\{Y(t)\}\) is a solution of equation (5) and \(H>\frac{1}{\alpha }\) then it is long range dependent in the sense of codifference and L\(\acute{e}\) vy correlation cascade.

The last theorem corresponding to the 1st type of the Ornstein-Uhlenbeck model based on long memory process is related to the fact that ratio of two considered measures, namely codifference and covariation are limited. Similar results we have obtained for the Ornstein-Uhlenbeck process with \(\alpha -\) stable L\(\acute{e}\)vy motion, where we have proved the more strong property, namely the ratio CD/CV as a limit is equal to \(\alpha \) [38]. This property is also satisfied for discrete version of the Ornstein-Uhlenbeck process with \(\alpha -\) stable L\(\acute{e}\)vy motion, namely, autoregressive time series of order 1 with \(\alpha -\)stable distribution [61]. See also [22, 62].

Theorem 4.14

If the process \(\{Y(t)\}\) is a solution of equation (5), \(1/\alpha<H<1\) and \(1<\alpha <2\) then the following holds:

$$\begin{aligned} \left| \frac{CD(Y(t),Y(0))}{CV(Y(t),Y(0))}\right| \le 2\alpha +1,~t\rightarrow -\infty . \end{aligned}$$

Proof

Taking into account the Theorems 4.11 and 4.12 for \(t\rightarrow -\infty \) , we obtain:

$$\begin{aligned} \left| \frac{CD(Y(t),Y(0))}{CV(Y(t),Y(0))}\right| =\left| \frac{k(\alpha ,H)}{c_1(\alpha ,H)}\right| , \end{aligned}$$

where

$$\begin{aligned}&k(\alpha ,H)\\&\quad =a^{-\alpha }(b(H-1/\alpha ))^{\alpha }\\&\qquad \left[ \int _{1}^{\infty }\left| (x-1)^{H-1/\alpha -1}\right| ^{\alpha } +\left| x^{H-1/\alpha -1}\right| ^{\alpha }\right. \\&\qquad \quad \left. -\left| (x-1)^{H-1/\alpha -1} -x^{H-1/\alpha -1}\right| ^{\alpha }\right] dx\\&c_1(\alpha ,H)=a^{-\alpha }(b(H-1/\alpha ))^{\alpha }\\&\qquad \int _{1}^{\infty }(x-1)^{(H-1/\alpha -1)(\alpha -1)}x^{(H-1/\alpha -1)}dx. \end{aligned}$$

Next we take into account formula (2.7) in [21], namely for any real numbers r and s for \(1<\gamma \le 2\) the following holds:

$$\begin{aligned} \left| |r+s|^{\gamma }-|r|^{\gamma }-|s|^{\gamma }\right| \le \gamma |r||s|^{\gamma -1}+(\gamma +1)|r|^{\gamma } \end{aligned}$$

and apply it to the integrated function in the definition of \(k(\alpha ,H)\). We obtain then:

$$\begin{aligned}&\left| \frac{k(\alpha ,H)}{c_1(\alpha ,H)}\right| \\&\quad \le \frac{\alpha \int _{1}^{\infty }(x-1)^{(H-1/\alpha -1)(\alpha -1)} x^{(H-1/\alpha -1)}dx+(\alpha +1)\int _{1}^{\infty }x^{(H-1/\alpha -1)\alpha }dx}{\int _{1}^{\infty }(x-1)^{(H-1/\alpha -1)(\alpha -1)}x^{(H-1/\alpha -1)}dx}\\&\quad =\alpha +(\alpha +1)\\&\qquad \frac{\int _{1}^{\infty }x^{(H-1/\alpha -1)\alpha }dx}{\int _{1}^{\infty } (x-1)^{(H-1/\alpha -1)(\alpha -1)}x^{(H-1/\alpha -1)}dx}. \end{aligned}$$

It is easy to show \(\int _{1}^{\infty }x^{(H-1/\alpha -1)\alpha }dx =\frac{1}{\alpha (1-H)}\). Moreover for \(1/\alpha<H<1\) and \(1<\alpha <2\) we have:

$$\begin{aligned}&\int _{1}^{\infty }(x-1)^{(H-1/\alpha -1)(\alpha -1)}x^{(H-1/\alpha -1)}dx\\&\quad =\int _{0}^{\infty }\left( \frac{1}{x}\right) ^{-(H-1/\alpha -1)(\alpha -1)} \left( \frac{1}{x+1}\right) ^{-(H-1/\alpha -1)}dx\\&\quad \ge \int _{0}^{\infty }\left( \frac{1}{x+1}\right) ^{-(H-1/\alpha -1)\alpha }dx =\frac{1}{\alpha (1-H)}. \end{aligned}$$

Therefore, we obtain the thesis. \(\square \)

4.2 The 2nd type of the Ornstein-Uhlenbeck model based on long memory process

Theorem 4.21

If \(\{Y^{*}(t)\}\) is a solution of (9) given by equation 11and \((kappa-2)(\alpha -1)>-1\) then the codifference of \(Y^{*}(t)\) on \(Y^{*}(0)\) satisfies:

$$\begin{aligned}&CD(Y^{*}(t), Y^{*}(0)) \nonumber \\&\quad =\left| t\right| ^{\alpha (k-1)+1-\alpha } \frac{b^\alpha |\kappa -1|^\alpha }{|\varGamma ^\alpha (\kappa )|a^\alpha } \int _{-\infty }^0 \left| (1-w)^{\kappa -2}+(-w)^{\kappa -2}\right| ^\alpha \nonumber \\&\qquad -\left| (1-w)^{\kappa -2}\right| ^\alpha -\left| (-w)^{\kappa -2}\right| ^\alpha \,dw, ~~\text{ as }~~t\rightarrow \infty . \end{aligned}$$
(26)

Proof

$$\begin{aligned}&CD(Y^{*}(t),Y^{*}(0))\\&\quad =\int \limits _{-\infty }^0 \Bigg |\frac{b\left( \kappa -1\right) }{\varGamma (\kappa )} \int _s^t\left( u-s+1\right) ^{\kappa -2}e^{-a(t-u)} \\&\qquad +\frac{b\left( \kappa -1\right) }{\varGamma (\kappa )} \int _s^0\left( u-s+1\right) ^{\kappa -2}e^{a(u)}du \\&\qquad + \frac{b}{\varGamma (\kappa )}e^{-a(t-s)} +\frac{b}{\varGamma (\kappa )}e^{a(s)}\Bigg |^\alpha ds\\&\qquad -\int \limits _{-\infty }^{0}\Bigg |\frac{b\left( \kappa -1\right) }{\varGamma (\kappa )} \int _s^t\left( u-s+1\right) ^{\kappa -2}\\&\qquad \qquad e^{-a(t-u)} + \frac{b}{\varGamma (\kappa )}e^{-a(t-s)} \Bigg |^\alpha ds\\&\qquad -\int \limits _{-\infty }^{0}\Bigg |\frac{b\left( \kappa -1\right) }{\varGamma (\kappa )} \int _s^0\left( u-s+1\right) ^{\kappa -2}\\&\qquad \qquad e^{au}du + \frac{b}{\varGamma (\kappa )}e^{as} \Bigg |^\alpha ds. \end{aligned}$$

Now changing the variables as \(u=vt\) and \(s=wt\) , we get:

$$\begin{aligned}&CD(Y^{*}(t),Y^{*}(0))\\&\quad =\int \limits _{-\infty }^0 t\Bigg |\frac{b\left( \kappa -1\right) }{\varGamma (\kappa )} \int _w^1\left( vt-ut+1\right) ^{\kappa -2}e^{-a(t-vt)}t\,dv \\&\qquad +\frac{b\left( \kappa -1\right) }{\varGamma (\kappa )}\int _w^0 \left( vt-wt+1\right) ^{\kappa -2}e^{avt}t\,dv \\&\qquad + \frac{b}{\varGamma (\kappa )}e^{-a(t-wt)} +\frac{b}{\varGamma (\kappa )}e^{awt}\Bigg |^\alpha t\,dw\\&\qquad -\int \limits _{-\infty }^{0}\Bigg |\frac{b\left( \kappa -1\right) }{\varGamma (\kappa )} \int _w^1\left( vt-wt+1\right) ^{\kappa -2}\\&\qquad \qquad e^{-a(t-tv)} t\,dv + \frac{b}{\varGamma (\kappa )} e^{-a(t-wt)} \Bigg |^\alpha t\,dw\\&\qquad -\int \limits _{-\infty }^{0}\Bigg |\frac{b\left( \kappa -1\right) }{\varGamma (\kappa )} \int _w^0\left( vt-wt+1\right) ^{\kappa -2}\\&\qquad \qquad e^{avt} t\,dv + \frac{b}{\varGamma (\kappa )}e^{awt} \Bigg |^\alpha t\,dw. \end{aligned}$$

Then denoting as:

$$\begin{aligned} f(t,w)&=\frac{b\left( \kappa -1\right) }{\varGamma (\kappa )} \int _w^1\left( v-w+\frac{1}{t}\right) ^{\kappa -2}\nonumber \\&\quad e^{-a(t-tv)} \,dv + \frac{b}{\varGamma (\kappa )t^{k-1}}e^{-a(t-wt)} \end{aligned}$$
(27)

and

$$\begin{aligned} g(t,w)&=\frac{b\left( \kappa -1\right) }{\varGamma (\kappa )} \int _w^0\left( v-w+\frac{1}{t}\right) ^{\kappa -2}\nonumber \\&\quad e^{-atv} \,dv + \frac{b}{\varGamma (\kappa )t^{k-1}}e^{awt} \end{aligned}$$
(28)

we observe that:

$$\begin{aligned}&CD(Y^{*}(t),Y^{*}(0))\nonumber \\&\quad =|t|^{\alpha (k-1)+1}\nonumber \\&\qquad \int \limits _{-\infty }^0 \left( \left| f(t,w)+g(t,w) \right| ^\alpha -\left| f(t,w) \right| ^\alpha -\left| g(t,w) \right| ^\alpha \right) \,dw. \end{aligned}$$
(29)

Now taking into account Lemma 5.2 [37] with \(r=tf(t,w)\) and \(s=tg(t,w)\) and Lemma 4.21 in [37], we get:

$$\begin{aligned}&\left| tf(t,w)+tg(t,w) \right| ^\alpha -\left| tf(t,w) \right| ^\alpha -\left| tg(t,w) \right| ^\alpha \\&\quad \le \alpha \left| tf(t,w) \right| \left| tg(t,w) \right| ^{\alpha -1} +(\alpha +1)\left| tf(t,w) \right| ^\alpha \\&\quad \le \alpha \left( \frac{b}{\varGamma (\kappa )} \Big (\frac{|\kappa -1|}{2^{\kappa -2}a}(1-w)^{\kappa -2}+Ne^{a/2 (w-1)}\Big )\right) \\&\qquad \left( \frac{b}{\varGamma (\kappa )}\Big (\frac{|\kappa -1|}{2^{\kappa -2}a} (-w)^{\kappa -2}+\tilde{N}e^{a/2 w}\Big )\right) ^{\alpha -1}\\&\qquad +(\alpha -1)\left( \frac{b}{\varGamma (\kappa )} \Big (\frac{|\kappa -1|}{2^{\kappa -2}a}(1-w)^{\kappa -2}+Ne^{a/2 (w-1)}\Big )\right) ^\alpha \end{aligned}$$

which belongs to \(L^1(-\infty , 0)\). Thus, altogether applying dominated convergence theorem and Lemma 4.22 we obtain that:

$$\begin{aligned}&CD(Y^{*}(t), Y^{*}(0))\\&\quad =\left| t\right| ^{\alpha (k-1)+1-\alpha } \frac{b^\alpha |\kappa -1|^\alpha }{|\varGamma ^\alpha (\kappa )|a^\alpha }\\&\qquad \int _{-\infty }^0 \left| (1-w)^{\kappa -2}+(-w)^{\kappa -2}\right| ^\alpha -\left| (1-w)^{\kappa -2}\right| ^\alpha \\&\qquad -\left| (-w)^{\kappa -2}\right| ^\alpha \,dw~~\text{ as }~~t\rightarrow \infty . \end{aligned}$$

\(\square \)

Lemma 4.21

If we assume \(t \ge 1\) and \(w\le 0\), then the following conditions hold:

$$\begin{aligned}&\left| tf(t,w)\right| \le \frac{b}{|\varGamma (\kappa )|} \Big (\frac{|\kappa -1|}{2^{\kappa -2}a}(1-w)^{\kappa -2}+Ne^{a/2 (w-1)}\Big )\\&\left| tg(t,w)\right| \le \frac{b}{|\varGamma (\kappa )|} \Big (\frac{|\kappa -1|}{2^{\kappa -2}a}(-w)^{\kappa -2}+\tilde{N}e^{a/2 (w)}\Big ), \end{aligned}$$

where \(N>0\) and \(\tilde{N}>0\) are finite constants while f and g are given in (27) and (28), respectively.

Proof

Let us prove the first part since the second follows immediately.

$$\begin{aligned}&\left| tf(t,w)\right| \\&\quad =\left| \frac{bt}{\varGamma (\kappa )}\left( (\kappa -1) \int _{w}^{1}\left( v-w+\frac{1}{t}\right) ^{\kappa -2}\right. \right. \\&\qquad \quad \left. \left. e^{a(vt-1)}\,dv+\frac{1}{t^{\kappa -1}}e^{-a(t-wt)} \right) \right| \\&\quad =\left| \frac{bt}{\varGamma (\kappa )}\left( \frac{(\kappa -1)}{t} \int _{t(w-1)}^{0}\left( \frac{u}{t}+1-w+\frac{1}{t}\right) ^{\kappa -2}\right. \right. \\&\qquad \quad \left. \left. e^{au}\,du+\frac{1}{t^{\kappa -1}}e^{-a(t-wt)} \right) \right| \\&\quad =\Big |\frac{bt}{\varGamma (\kappa )}\Bigg (\frac{(\kappa -1)}{t} \int _{t(w-1)}^{t/2(w-1)}\left( \frac{u}{t}+1-w+\frac{1}{t}\right) ^{\kappa -2}\\&\qquad \quad e^{au}\,du +\frac{(\kappa -1)}{t}\int _{t/2(w-1)}^{0} \left( \frac{u}{t}+1-w+\frac{1}{t}\right) ^{\kappa -2}\\&\qquad \quad e^{au}\,du+\frac{1}{t^{\kappa -1}}e^{-a(t-wt)} \Bigg ) \Big |\\&\quad \le \frac{bt}{|\varGamma (\kappa )|}\Bigg (\left| \frac{(\kappa -1)}{t} \int _{t(w-1)}^{t/2(w-1)}\left( \frac{u}{t}+1-w+\frac{1}{t}\right) ^{\kappa -2}\right. \\&\qquad \quad \left. e^{au}\,du\right| +\left| \frac{(\kappa -1)}{t}\int _{t/2(w-1)}^{0} \left( \frac{u}{t}+1-w+\frac{1}{t}\right) ^{\kappa -2}\right. \\&\qquad \quad \left. e^{au}\,du\right| +\left| \frac{1}{t^{\kappa -1}}e^{-a(t-wt)} \right| \Bigg )\\&\quad =\frac{b}{|\varGamma (\kappa )|}\Bigg (\frac{|\kappa -1|}{t^{\kappa -2}a} \left( e^{a(tw-t)}-e^{a/2(tw-t)}\right) \\&\qquad +\frac{|\kappa -1|}{2^{k-2}a}(1-w)^{\kappa -2}(1-e^{a/2(wt-t)}) +\frac{1}{t^{\kappa -2}}e^{a(wt-t)}\Bigg ). \end{aligned}$$

Since \(w\le 0\) and \(\frac{1}{t^{\kappa -2}}e^{a(wt-t)} <\frac{1}{t^{\kappa -2}}e^{a/2(wt-t)} \). Moreover functions of the form \(\frac{1}{t^{\kappa -2}}e^{a/2(wt-t)}\) attain their maximum \(M>0\), thus we get for every \(w\le 0\) and for every \(t>1\)

$$\begin{aligned} \frac{1}{t^{\kappa -1}}e^{a/2(wt-t)}\le M e^{a/2(w-1)}, \end{aligned}$$

which is obviously integrable for \(w \in (-\infty ,0)\) Thus, finally we obtain that:

$$\begin{aligned} \left| tf(t,w)\right|&\le \frac{b}{|\varGamma (\kappa )|} \Big (\frac{|\kappa -1|}{2^{\kappa -2}a}(1-w)^{\kappa -2}+Ne^{a/2 (w-1)}\Big ) \end{aligned}$$

for some constant \(N>0\). \(\square \)

It is important to note the limiting behavior (when \(t\rightarrow \infty \)) of the functions tf(t, w) and tg(t, w), where f and g are given in (27) and (28), respectively.

Lemma 4.22

For functions tf(t, w) and tg(t, w), we have the following limits as \(t\rightarrow \infty \):

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }tf(t,w) =\frac{b(\kappa -1)}{a\varGamma (\kappa )}(1-w)^{\kappa -2}, \end{aligned}$$
(30)
$$\begin{aligned} \lim \limits _{t\rightarrow \infty }tg(t,w) =\frac{b(\kappa -1)}{a\varGamma (\kappa )}(-w)^{\kappa -2}. \end{aligned}$$
(31)

Proof

We only prove equation 30 since the latter follows from Lemma 5.4 in [37].

$$\begin{aligned}&\lim \limits _{t\rightarrow \infty }tf(t,w) \\&\quad = \lim \limits _{t\rightarrow \infty }t\left( \frac{b(\kappa -1)}{\varGamma (\kappa )} \int _w^1\left( v-w+\frac{1}{t}\right) ^{\kappa -2}\right. \\&\qquad \quad \left. e^{-a(t-tv)} \,dv + \frac{b}{\varGamma (\kappa )t^{k-1}}e^{-a(t-wt)} \right) \\&\quad = \lim \limits _{t\rightarrow \infty }\left( \frac{b(\kappa -1)}{\varGamma (\kappa )} \int _{t(w-1)}^0\left( \frac{z}{t}+1-w+\frac{1}{t}\right) ^{\kappa -2}\right. \\&\qquad \quad \left. e^{az} \,dz + \frac{b}{\varGamma (\kappa )t^{\kappa -2}}e^{-a(t-wt)} \right) \\&\quad = \lim \limits _{t\rightarrow \infty }\left( \frac{b(\kappa -1)}{\varGamma (\kappa )} \int _{t(w-1)}^{t(w-1/2)}\left( \frac{z}{t}+1-w+\frac{1}{t}\right) ^{\kappa -2}\right. \\&\qquad \quad \left. e^{az} \,dz + \frac{b}{\varGamma (\kappa )t^{\kappa -2}}e^{-a(t-wt)} \right) \\&\qquad + \lim \limits _{t\rightarrow \infty }\left( \frac{b(\kappa -1)}{\varGamma (\kappa )} \int _{t(w-1/2)}^{0}\left( \frac{z}{t}+1-w+\frac{b}{t}\right) ^{\kappa -2}e^{az} \,dz\right) \\&\quad =: f_1+f_2. \end{aligned}$$

We have:

$$\begin{aligned}&\frac{b(\kappa -1)}{\varGamma (\kappa )}\int _{t(w-1)}^{t(w-1/2)} \left( \frac{z}{t}+1-w+\frac{1}{t}\right) ^{\kappa -2}\\&\qquad e^{az} \,dz + \frac{b}{\varGamma (\kappa )t^{\kappa -2}}e^{-a(t-wt)} \\&\quad \le \frac{b}{\varGamma (\kappa )} e^{at(w-1/2)} \left( \left( w-\frac{1}{2}+1-w+\frac{1}{t} \right) ^{\kappa -1} -\left( \frac{1}{t} \right) ^{\kappa -1} \right) \\&\qquad +\frac{b}{\varGamma (\kappa )t^{\kappa -2}}e^{-a(t-wt)} \end{aligned}$$

thus as \(t\rightarrow \infty \) the above goes to zero. Now, for the remaining term we have:

$$\begin{aligned}&\frac{b(\kappa -1)}{\varGamma (\kappa )}\int _{t(w-1/2)}^{0} \left( \frac{z}{t}+1-w+\frac{1}{t}\right) ^{\kappa -2}e^{az} \,dz \\&\quad =\frac{b(\kappa -1)}{\varGamma (\kappa )} \int _{-\infty }^0 {\mathbb {1}}_{\{t(w-1/2) \le z 0 \}}\\&\qquad \left( \frac{z}{t}+1-w+\frac{1}{t}\right) ^{\kappa -2}e^{az} \,dz \end{aligned}$$

and

$$\begin{aligned}&{\mathbb {1}}_{\{t(w-1/2)\le z\le 0 \}}\left( \frac{z}{t} +1-w+\frac{1}{t}\right) ^{\kappa -2}\nonumber \\&\quad e^{az} \,dz \le \left( \frac{1}{2} \right) ^{\kappa -2}e^{az} \end{aligned}$$
(32)

which is integrable in the interval \((-\infty , 0)\). \(\square \)

Theorem 4.22

Let \(\{Y^{*}(t)\}\) be a solution of (9) given in equation 11, then for \((\kappa -2)(\alpha -1)>-1\) the covariation of \(Y^{*}(t)\) on \(Y^{*}(0)\) fullfills:

$$\begin{aligned}&CV(Y^{*}(t),Y^{*}(0))\nonumber \\&\quad =|t|^{(\kappa -1)\alpha +1-\alpha } \frac{b^\alpha |(\kappa -1)|^\alpha }{a^\alpha |\varGamma ^\alpha (\kappa )|}\nonumber \\&\qquad \int \limits _{-\infty }^{0}(1-w)^{\kappa -2}(-w)^{(\alpha -1)(\kappa -2)} \,dw~~\text{ as }~~t\rightarrow \infty . \end{aligned}$$
(33)

Proof

$$\begin{aligned}&CV(Y^{*}(t),Y^{*}(0)) \\&\quad =\frac{b^\alpha |(\kappa -1)|}{|\varGamma ^\alpha (\kappa )|} \int \limits _{-\infty }^{0}\\&\qquad \left( \int _s^t (u-s+1)^{\kappa -2}e^{-a(t-u)}\,du+e^{-a(t-s)} \right) \\&\qquad \left( \int _s^0 (u-s+1)^{\kappa -2}e^{au}\,du+e^{as} \right) ^{\alpha -1}ds. \end{aligned}$$

Changing the variables \(u=vt\) and \(s=wt\) , we get:

$$\begin{aligned}&CV(Y^{*}(t),Y^{*}(0)) \\&\quad =\frac{b^\alpha |\kappa -1|}{|\varGamma ^\alpha (\kappa )|} \int \limits _{-\infty }^{0}\\&\qquad \left( \int _w^1 (vt-wt+1)^{\kappa -2}e^{-a(t-vt)}\,dv+e^{-a(t-wt)} \right) \\&\qquad \left( \int _w^0 (vt-wt+1)^{\kappa -2}e^{atv}\,dv+e^{awt} \right) ^{\alpha -1}t\,dw\\&\quad =\left| t\right| ^{\alpha (k-1)+1}\frac{b^\alpha |\kappa -1|}{|\varGamma ^\alpha (\kappa )|} \int \limits _{-\infty }^{0}\\&\qquad \left( \int _w^1 (v-w+\frac{1}{t})^{\kappa -2}e^{-a(t-vt)}\,dv +\frac{e^{-a(t-wt)}}{t^{\kappa -1}} \right) \\&\qquad \left( \int _w^0 (v-w+\frac{1}{t})^{\kappa -2}e^{avt}\,dv +\frac{e^{awt}}{{t^{\kappa -1}}} \right) ^{\alpha -1}\,dw. \end{aligned}$$

Now, using Lemma 4.22 applying dominated convergence theorem we obtain that:

$$\begin{aligned}&CV(Y^{*}(t),Y^{*}(0)) \\&\quad =|t|^{(\kappa -1)\alpha +1-\alpha } \frac{b^\alpha |\kappa -1|^\alpha }{a^\alpha |\varGamma ^\alpha (\kappa )|}\\&\qquad \int \limits _{-\infty }^{0}(1-w)^{\kappa -2}(-w)^{(\alpha -1) (\kappa -2)}\,dw~~\text{ as }~~t\rightarrow \infty . \end{aligned}$$

\(\square \)

Theorem 4.23

Let \(\{Y^{*}(t)\}\) is a solution of (9) given by equation 11, then the correlation cascade of \(Y^{*}(t)\) on \(Y^{*}(0)\) fulfils:

$$\begin{aligned} C_l(0,t)&=t^{\alpha (\kappa -1)+1-\alpha }\frac{2}{|\varGamma ^\alpha (\kappa )|l^\alpha \alpha }\nonumber \\&\quad \left( \frac{b|\kappa -1|}{a}\right) ^{\alpha }\int _1^\infty w^{\alpha (k-2)}\,dw\nonumber \\&=t^{\alpha (\kappa -1)+1-\alpha }\frac{2}{|\varGamma ^\alpha (\kappa )|l^\alpha \alpha }\nonumber \\&\quad \left( \frac{b|\kappa -1|}{a}\right) ^{\alpha }\frac{1}{\alpha (\kappa -2)+1} ~~\text{ as }~~t\rightarrow \infty . \end{aligned}$$
(34)

Proof

$$\begin{aligned} C_l(0,t)&= \frac{2b^\alpha }{|\varGamma ^\alpha (\kappa )|l^\alpha \alpha }\\&\quad \int \limits _{t}^{\infty }\Big | (\kappa -1)\int _0^y (x+1)e^{a(y-x)} \,dx+e^{-ay}\Big |^\alpha \, dy \end{aligned}$$

After changing the variables twice, we get:

$$\begin{aligned} C_l(0,t)&= \frac{2b^\alpha }{|\varGamma ^\alpha (\kappa )|l^\alpha \alpha }\\&\quad \int \limits _{1}^{\infty }\Big | (\kappa -1)\int _0^w (vt+1) e^{a(wt-vt)}\,t dv+e^{-awt}\Big |^\alpha \, t dw\\&=\frac{2b^\alpha }{|\varGamma ^\alpha (\kappa )|l^\alpha \alpha }|t|^{\alpha (k-1)+1}\\&\quad \int \limits _{1}^{\infty }\Big | (\kappa -1)\int _0^w \left( v+\frac{1}{t}\right) ^{\kappa -2}e^{a(wt-vt)}\, dv +\frac{e^{-awt}}{t^{\kappa -1}}\Big |^\alpha \, dw\\&=\frac{2b^\alpha }{|\varGamma ^\alpha (\kappa )|l^\alpha \alpha }|t|^{\alpha (k-1)+1}\\&\quad \int \limits _{1}^{\infty }\Big | (\kappa -1)\int _{-\infty }^0 {\mathbb {1}}_{\{-wt\le u\le 0\}}\\&\quad \left( \frac{u}{t}+w+\frac{1}{t}\right) ^{\kappa -2} e^{au}\, \frac{du}{t}+\frac{e^{-awt}}{t^{\kappa -1}}\Big |^\alpha \, dw. \end{aligned}$$

Now we can show similarly as previously that the function:

$$\begin{aligned} th(t,w)= & {} t(\kappa -1)\int _{-\infty }^0 {\mathbb {1}}_{\{-wt\le u\le 0\}}\\&\left( \frac{u}{t}+w+\frac{1}{t}\right) ^{\kappa -2}e^{au}\, \frac{du}{t} +\frac{e^{-awt}}{t^{\kappa -2}} \end{aligned}$$

is bounded. Application of the dominated convergence theorem yields:

$$\begin{aligned}&\lim \limits _{t\rightarrow \infty } C_l(0,t)t^{\alpha -\alpha (\kappa -1)-1}\\&\quad =\lim \limits _{t\rightarrow \infty } \frac{2b^\alpha }{|\varGamma ^\alpha (\kappa )|l^\alpha \alpha }\\&\qquad \int \limits _{1}^{\infty }\Big | (\kappa -1)\int _{-\infty }^0 {\mathbb {1}}_{\{-wt\le u\le 0 \}}\\&\qquad \left( \frac{u}{t}+w+\frac{1}{t}\right) ^{\kappa -2} e^{au}\, du+\frac{e^{-awt}}{t^{\kappa -2}}\Big |^\alpha \, dw\\&\quad =\frac{2b^\alpha }{|\varGamma ^\alpha (\kappa )|l^\alpha \alpha } \left( \frac{b|\kappa -1|}{a}\right) ^{\alpha }\int _1^\infty w^{\alpha (k-2)}\,dw\\&\quad =\frac{2b^\alpha }{|\varGamma ^\alpha (\kappa )|l^\alpha \alpha } \left( \frac{b|\kappa -1|}{a}\right) ^{\alpha }\frac{1}{\alpha (\kappa -2)+1}. \end{aligned}$$

\(\square \)

Similarly, as in the case of the 1st type of long memory Ornstein-Uhlenbeck model based on long memory process we can formulate the following corollaries for the 2nd type.

Corollary 4.21

If the process \(\{Y^{*}(t)\}\) is a solution of equation (9) then it is mixing.

Proof

Again it easily follows from Theorem 1 in [15].

Moreover, since in the sense of codifference or correlation cascade we have that both of these measures of dependence decay proportionally to \(|t|^{\alpha (\kappa -1)+1-\alpha }\) we also have the following corollary. \(\square \)8

Corollary 4.22

If the process \(\{Y^{*}(t)\}\) is a solution of equation (9) with \(\alpha >1\) then it is not long range dependent in the sense of codifference and L\(\acute{e}\) vy correlation cascade.

Similar as for the process \(\{Y(t)\}\) we can prove the ratio of two measures of dependence for the 2nd type of the Ornstein-Uhlenbeck model based on long memory process is limited.

Theorem 4.24

If the process \(\{Y^{*}(t)\}\) is a solution of equation (9), \(\kappa <1-1/\alpha \), \(1<\alpha <2\), then the following holds:

$$\begin{aligned} \left| \frac{CD(Y^{*}(t),Y^{*}(0))}{CV(Y^{*}(t),Y^{*}(0))}\right| \le 2\alpha +1,~t\rightarrow \infty . \end{aligned}$$

Proof

Taking into account the Theorems 4.21 and 4.22 for \(t\rightarrow \infty \) , we obtain:

$$\begin{aligned}&\left| \frac{CD(Y^{*}(t),Y^{*}(0))}{CV(Y^{*}(t),Y^{*}(0))}\right| \\&\quad =\frac{\int _{-\infty }^0 \left| (1-w)^{\kappa -2}+(-w)^{\kappa -2}\right| ^\alpha -\left| (1-w)^{\kappa -2}\right| ^\alpha -\left| (-w)^{\kappa -2}\right| ^\alpha \,dw}{\int \limits _{-\infty }^{0}(1-w)^{\kappa -2}(-w)^{(\alpha -1)(\kappa -2)}\,dw}. \end{aligned}$$

Similar as previously, we take into account formula (2.7) in [21], and we get:

$$\begin{aligned}&\left| \frac{CD(Y^{*}(t),Y^{*}(0))}{CV(Y^{*}(t),Y^{*}(0))}\right| \\&\quad \le \frac{\alpha \int \limits _{-\infty }^{0}(1-w)^{\kappa -2}(-w)^{(\alpha -1)(\kappa -2)} \,dw+(\alpha +1)\int \limits _{-\infty }^{0}(1-w)^{(\kappa -2)\alpha }dw}{\int \limits _{-\infty }^{0}(1-w)^{\kappa -2}(-w)^{(\alpha -1)(\kappa -2)}\,dw}\\&\quad =\alpha +(\alpha +1)\frac{\int \limits _{-\infty }^{0}(1-w)^{(\kappa -2) \alpha }dw}{\int \limits _{-\infty }^{0}(1-w)^{\kappa -2}(-w)^{(\alpha -1)(\kappa -2)}\,dw}. \end{aligned}$$

It is easy to show \(\int \limits _{-\infty }^{0} (1-w)^{(\kappa -2)\alpha }dw =\frac{1}{(2-\kappa )\alpha -1}\). Moreover, for \(\kappa <1-1/\alpha \) and \(1<\alpha <2\) we have:

$$\begin{aligned}&\int \limits _{-\infty }^{0}(1-w)^{\kappa -2}(-w)^{(\alpha -1)(\kappa -2)}\,dw\\&\quad =\int \limits _{0}^{\infty }\left( \frac{1}{1+w}\right) ^{-(\kappa -2)} \left( \frac{1}{w}\right) ^{-(\alpha -1)(\kappa -2)}\,dw\\&\quad \ge \int \limits _{0}^{\infty }\left( \frac{1}{1+w}\right) ^{-(\kappa -2)\alpha } \,dw=\frac{1}{(2-\kappa )\alpha -1}. \end{aligned}$$

This gives the thesis. \(\square \)

5 Conclusions

In this paper, we have analyzed two Ornstein-Uhlenbeck models based on long memory prcesses. Because those processes are based on the \(\alpha -\)stable system, therefore the long range dependence is expressed here in the language of measures adequate for models with infinite variance, namely codifference and L\(\acute{e}\)vy correlation cascade defined for infinitely divisible systems. We have introduced the mentioned processes and showed its integral forms that is useful in the calculation of their main properties. We study the asymptotic behavior of alternative measures of dependence for examined systems. In addition, we have analyzed the covariation, the measure defined only for \(\alpha -\)stable processes. We have indicated the ratio of codifference and covariation is limited which in some sense is an extension of the previous results for Ornstein-Uhlenbeck process-based \(\alpha \)-stable L\(\acute{e}\)vy motion. This property can be a starting point to introduction a new estimator of stability index for Ornstein-Uhlenbeck model based on long memory processes. We hope the obtained results in this paper can be extended to more advanced systems with long memory behavior.