1 Introduction

The rising deployment of multiple small satellites flying in formation rather than one large satellite offers benefits such as increased flexibility, reliability and efficiency of future satellite missions. This concept follows the ongoing change in the space industry, resulting in increased launch cycles and decreasing transport prices, giving it the potential to become a state-of-the-art technology. However, one difficulty is the use of complex chemical or electrical propulsion systems for the individual satellites, which due to their sophisticated design account for a significant proportion of the weight and manufacturing costs. A promising alternative to this system is the exploitation of the residual atmosphere to create and maintain the satellite formation via differential aerodynamic forces (see Fig. 1 for a conceptual visualization). This methodology offers the unique possibility to take advantage of the benefits of both, distributed satellite systems [1] and very low earth orbits (VLEO) [2], without the need of a dedicated thrusting device and is consequently of highest interest to the CubeSat community. Notably, differential drag has already been successfully applied in-orbit (e.g., by the Planet Lab constellation [3], the ORBCOMM constellation [4], the AeroCube-4 CubeSats [5] or the S-NET formation [6]).

Fig. 1
figure 1

Conceptual visualization of two satellites flying in formation using their satellite’s solar panel as dedicated drag/lift plates [7]

Full size image

At the Institute of Space Systems (IRS) of the University of Stuttgart, this methodology is investigated since 2018. A comprehensive and state-of the art literature and gap analysis can be found in [7] as well as an overview of the progress achieved so far in [8]. A major goal is the development and enhancement of simplified rendezvous maneuver algorithms, which are fast and computationally inexpensive and thus can be applied in Monte Carlo simulations.

1.1 Historic algorithm developments

The foundation for the development of these algorithms was laid by Leonard, who proposed using differential drag for the in-plane relative motion control in her master thesis published in 1986 [9, 10]. The accuracy of the algorithm was increased by Bevilacqua and Romano in 2008 [11], who replaced the Clohessy–Wiltshire (CW) equations [12] by the \({J}_{2}\) inclusive Schweighardt-Sedwick (SS) equations [13]. In 2011, Horsley et al. [14] extended the algorithm to enable to control all translational degrees of freedom using differential lift for the out-of-plane control using the CW equations. Then, in 2015, Shao et al. refined the accuracy of Horsley et al.’s algorithm again by replacing the CW equations by the SS equations [15]. In 2017, Smith et al. [16] investigated the extent to which the simple trajectories are applicable to spacecraft formations under changing initial conditions and addressed impracticalities and collision risks associated with the differential lift-based trajectories. The latter necessitated to switch the order of the three-phased rendezvous maneuver as proposed by Horsley et al. [14], which resulted in the following updated sequence which is used and referred to as throughout the rest of this article:

  • Phase \(1\) zeroes out the average in-plane position;

  • Phase \(2\) zeroes out the out-of-plane motion;

  • Phase 3 zeroes out the oscillating in-plane states.

By applying Monte Carlo methods, Smith et al. [16] discovered that the third phase is successful if and only if the norm of the initial oscillating state vector \(\left({\alpha }_{P\mathrm{3,0}},\frac{{\beta }_{P\mathrm{3,0}}}{\sqrt{2cA}}\right)\), introduced in Eqs. (6) and (7), is within a certain range, the so-called feasibility range. If the initial conditions exceed this range, the algorithm is not able to design a successful rendezvous maneuver and since the overall maneuver success is dependent on the third phase, this renders the full maneuver unsuccessful. Options to enlarge the size of the range and therefore to increase the maneuver success were proposed in a CEAS Space Journal contribution in 2020 [7] and shown to be successful in a follow-up article published in the same journal later that year [17].

This article builds upon the two preceding articles and presents enhanced phase 3 algorithms which are not subjected to any limiting size and thus render all maneuvers successful which previously had to be denoted as unsuccessful due to algorithm limitations. In addition, a fast and precise option to determine the size of the feasibility range, which previously could only be determined using time consuming Monte Carlo simulations, is presented.

The article is structured as follows: First, the theoretical background and the underlying equations of motion are described in Sect. 2. Then, in Sect. 3, a method to determine the maximum possible reduction of eccentricity \(\Delta {e}_{\mathrm{max}}\) is proposed and verified. In Sect. 4, the enhanced phase 3 algorithms for differential lift or drag are presented. In the end, the developments are critically discussed and conclusions are drawn.

2 Background

2.1 Equations of motion

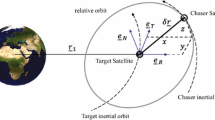
The equations of motion to describe the motion of the deputy spacecraft (also referred to as chaser) to the chief spacecraft (also referred to as target) utilized in this article are an intermediate set of the Schweighart-Sedwick (SS) equations [13], which take the \({J}_{2}\) perturbation caused by the Earth’s oblateness into account. The local-vertical/local-horizontal (LVLH) coordinate system, in which the SS equations are expressed, is centered at the chief’s center of mass. The \(\widehat{x}\)-axis runs from the Earth’s center through the chief’s center of mass. The \(\widehat{y}\)-axis points in the direction of motion and is orthogonal to the \(\widehat{x}\)-axis. The \(\widehat{z}\)-axis is orthogonal to the \(\widehat{x}\)- and \(\widehat{y}\)-axis and complements the right-handed system. The LVLH coordinate system is displayed in Figs. 1 and 2.

Fig. 2
figure 2

Definition of the LVLH coordinate system

Full size image

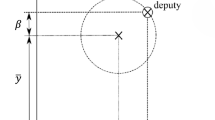
Leonard et al. proposed to decompose the deputy’s relative in-plane movement \((x,y)\) into an average component \((\stackrel{-}{x},\stackrel{-}{y})\) as well as an oscillating component \((\alpha ,\beta )\), which is applied throughout this article. The decomposed components of the deputy’s motion are displayed in Fig. 3. Notably, in the linearized form the in-plane relative motion is completely decoupled from the out-of-plane relative motion so that both can be controlled individually.

Fig. 3
figure 3

Reference target coordinate system

Full size image

In this article, the solutions to the SS equations including differential accelerations as suggested by Smith et al. [16] are employed. A slight correction to these equations was made in [7] and the corrected version is used in the following:

$$ x = \overline{x} + \alpha $$
(1)
$$ y = \overline{y} + \beta $$
(2)
$$ z = \left( {z_{0} - \frac{{a_{z} }}{{D^{2} \omega^{2} }}} \right)\cos \left( {D\omega t} \right) + \frac{{\dot{z}_{0} }}{D\omega }\sin \left( {D\omega t} \right) + \frac{{a_{z} }}{{D^{2} \omega^{2} }} $$
(3)

with \(\overline{x}\), \(\overline{y}\), \(\alpha\) and \(\beta\) being defined as:

$$ \overline{x} = \overline{x}_{0} + \frac{A}{\omega }a_{y} t $$
(4)
$$ \overline{y} = \overline{y}_{0} + B\omega \overline{x}_{0} t - \frac{A}{\omega }a_{x} t + \frac{AB}{2}a_{y} t^{2} $$
(5)
$$ \alpha = \left( {\alpha _{0} - \frac{{Aa_{x} }}{{2c\omega ^{2} }}} \right) \cdot \cos \left( {\sqrt {\frac{{2c}}{A}} \omega t} \right) + \frac{{Aa_{x} }}{{2c\omega ^{2} }} + \left( {\frac{{\beta _{0} }}{{\sqrt {2cA} }} - \frac{{A^{2} a_{y} }}{{2\omega ^{2} }}} \right) \cdot \sin \left( {\sqrt {\frac{{2c}}{A}} \omega t} \right), $$
(6)
$$\frac{\beta }{{\sqrt {2cA} }} = \left( {\frac{{\beta _{0} }}{{\sqrt {2cA} }} - \frac{{A^{2} a_{y} }}{{2\omega ^{2} }}} \right) \cdot \cos \left( {\sqrt {\frac{{2c}}{A}} \omega t} \right) + \frac{{A^{2} a_{y} }}{{2\omega ^{2} }} + \left( {\frac{{Aa_{x} }}{{2c\omega ^{2} }} - \alpha _{0} } \right) \cdot \sin \left( {\sqrt {\frac{{2c}}{A}} \omega t} \right). $$
(7)

The so-called SS coefficient \(c\) which takes the \(J_{2} \) influence into account, the auxiliary variables \(A\), \(B\) and \(D\) and ω, which is the angular velocity of the chief, are defined as follows:

$$ c = \sqrt {1 + \frac{{3J_{2} R_{{\text{E}}}^{2} }}{{8r_{{\text{c}}}^{2} }}\left( {1 + 3\cos \left( {2i_{{\text{c}}} } \right)} \right)} , $$
(8)
$$ A = \frac{2c}{{2 - c^{2} }} $$
(9)
$$ B = \frac{{2 - 5c^{2} }}{2c} $$
(10)
$$ D = \sqrt {3c^{2} - 2} $$
(11)
$$ \omega = \sqrt {\frac{{\mu_{{\text{E}}} }}{{r_{{\text{c}}}^{3} }}} . $$
(12)

Here \(R_{{\text{E}}}\) is the Earth’s mean radius, \(\mu_{{\text{E}}}\) is its gravitational parameter, \(i_{{\text{c}}}\) is the chief’s orbital inclination and \(r_{{\text{c}}}\) its orbital scalar radius. The parameters \(\overline{x}_{0}\), \(\overline{y}_{0}\), \(z_{0}\), \(\frac{{\dot{z}_{0} }}{D\omega }\), \(\alpha_{0}\) and \(\frac{{\beta_{0} }}{{\sqrt {2cA} }}\) are the initial conditions at the time \(t = 0\). \(a_{x}\), \(a_{y}\) and \(a_{z}\) are the accelerations of the deputy relative to the chief in the respective LVLH coordinate directions. These are induced by the differences in the aerodynamic drag and lift forces experienced by the two spacecraft which are created using dedicated drag and lift plates (Fig. 1). The influence of constant differential lift and drag on the phase planes is displayed in Fig. 4.

Fig. 4
figure 4

Phase plane for constant differential accelerations in a the x direction, b the y direction and c the z direction. A positive (negative) acceleration causes the state to move along the solid (dashed) trajectories [7]

Full size image

2.2 Original phase 3 algorithms

The original algorithm is divided up into three phases, in each of which a part of the relative motion is zeroed out (see Sect. 1). The terminology ‘original algorithm’ as used throughout this article refers to the algorithm developed by Smith et al. which is based on the work of Shao et al. [15], Horsley et al. [14] and Leonard et al. [9, 10]. Notably, initially (in the publication by Shao et al. [15] as well as Horsley et al. [14]), the order of phase 2 and 3 was reversed. However, Smith et al. [16] changed this order as thereby inevitably occurring collisions could be avoided. The focus of this article is phase 3 and the interested reader is referred to references [15, 17] for detailed information on phase 1 and 2. For phase 3, either differential drag or differential lift can be exploited. Consequently, two different algorithms are available. As an understanding of the original phase 3 algorithms for differential drag and lift is necessary to follow the developments presented hereinafter, these are shortly described in the following.

In case of a successful phase 3, the initial in-plane eccentricity of phase 3, \({e}_{P\mathrm{3,0}}\), defined as the vector norm of the initial oscillating state vector \(\left({\alpha }_{P\mathrm{3,0}},\frac{{\beta }_{P\mathrm{3,0}}}{\sqrt{2cA}}\right)\):

$${e}_{P\mathrm{3,0}}=\sqrt{{\alpha }_{P\mathrm{3,0}}^{2}+{\left(\frac{{\beta }_{P\mathrm{3,0}}}{\sqrt{2cA}}\right)}^{2}}$$
(13)

is fully zeroed out during the maneuver. As any in-plane control input inevitably also influences the already nullified position in the (\(\bar{x},\bar{y}\))–plane, it additionally has to be ensured that the final (\(f\)) average in-plane states after phase 3 are zero again (\({\bar{x}}_{f} = {\bar{y}}_{f}= 0\)). To achieve this, the overall duration during which a positive differential acceleration is commanded needs to match the duration during which a negative acceleration (\({t}_{-}\)) is commanded:

$$\sum {t}_{+}=\sum {t}_{-}$$
(14)

Before the original algorithms are discussed, the polar coordinate system depicted in Fig. 5, which will be used throughout this article, is introduced.

Here, the oscillating in-plane position of the deputy relative to the chief is expressed via the in-plane eccentricity \(e\), which is the norm of the oscillating in-plane state vector, defined as \(e= \sqrt{{\alpha }^{2}+\frac{{\beta }^{2}}{2cA}}\), and a phase angle \(\theta \) (\(\in [0;2\pi [\)), which is in the first quadrant defined as:

$$\theta =\mathrm{atan}\left(\frac{\alpha }{\beta } \cdot \sqrt{2cA}\right)$$
(15)

Notably, \(\theta \) is defined in a mathematically negative sense to follow the coasting direction of the deputy around the chief. Therefore, it needs to be calculated to match the definition shown in Fig. 5 for all other quadrants.

Fig. 5
figure 5

Polar coordinate system and definition of the phase angle \(\theta \)

Full size image

2.2.1 Original drag-based algorithm

The drag-based phase 3 control algorithm consists of an initial coasting period followed by three successive controlled segments during which differential drag accelerations \(\left({a}_{y}\right)\) are applied. The respective times of the three controlled segments are in the following referred to as \({t}_{1,d}\), \({t}_{2,d}\) and \({t}_{3,d}\) whereas the coasting period is refered to as \({t}_{c,d}\). Dependent on the initial conditions, either a \({t}_{+}/{t}_{-}/{t}_{+}\) (in the following referred to as pnp) or a \({t}_{-}/{t}_{+}/{t}_{-}\) (referred to as npn) sequence leads to the shorter maneuver time and is therefore chosen. Since any control input in the \(y\)-direction (\({a}_{y}\)) causes the (\(\bar{x},\bar{y}\))-states to move on a parabola in the phase plane (see Fig. 4), the following conditions for the time periods must hold to fulfill the condition stated in Eq. 14:

$${t}_{1,d}-{t}_{3,d}=0$$
(16)
$${t}_{2,d}-2\cdot {t}_{1,d}=0$$
(17)

As a consequence, it is sufficient to determine one of the three time periods as the two others can be calculated from Eq. (16) and (17). Before the control sequence is initiated, a coasting period in which no control input is commanded, is required in order for the deputy to reach the desired initial position.

The four required time periods \({t}_{c,d}\), \({t}_{1,d}\), \({t}_{2,d}\) and \({t}_{3,d}\) are determined by applying a backwards sequence (\(-{t}_{3,d}\)/\(-{t}_{2,d}\)/\({-t}_{1,d}\)/\(-{t}_{c,d}\)) starting from the origin (\(\mathrm{0,0}\)) of the \(\left(\alpha ,\frac{\beta }{\sqrt{2cA}}\right)\)-phase plane and enforcing the final eccentricity after the controlled sequence to match the initial eccentricity of phase 3 (\({e}_{P\mathrm{3,0}}\)). The resulting backwards sequence is as follows:

  1. 1.

    Starting at the origin (\(\mathrm{0,0}\)) and applying an acceleration for \(-{t}_{3,d}\) results in \({\alpha }_{3,d}\), \({\beta }_{3,d}\).

  2. 2.

    Starting at \({\alpha }_{3,d}, {\beta }_{3,d}\) and applying an acceleration (switched sign) for \(-{t}_{2,d}\) results in \({\alpha }_{2,d}, {\beta }_{2,d}\).

  3. 3.

    Starting at \({\alpha }_{2,d}, {\beta }_{2,d}\) and applying acceleration (switched sign) for \(-{t}_{1,d}\) results in \({\alpha }_{1,d}, {\beta }_{1,d}\). These are the states after the coasting period \({t}_{c,d}\) and the respective eccentricity is required to match \({e}_{P\mathrm{3,0}}\).

  4. 4.

    Starting at \(\left({\alpha }_{1,d},\frac{{\beta }_{1,d}}{\sqrt{2cA}}\right)\) an coasting without any control input for \(-{t}_{c,d}\) to the desired initial states \(\left({\alpha }_{P\mathrm{3,0}},\frac{{\beta }_{P\mathrm{3,0}}}{\sqrt{2cA}}\right)\).

This technique of applying a backwards sequence to solve for the maneuver time and/or position has already been described by Smith [18]. However, as the resulting equation which has to be solved for \({t}_{1,d}\) has never appeared in the literature, it is stated here for the sake of completeness. For a pnp sequence, applying a backwards sequence of phase 3 maneuvers sequence results in Eq. (18) which needs to be solved for \({t}_{1,d}\):

$${e}_{P\mathrm{3,0}}={\left({\left(2k\mathrm{sin}\left({t}_{1,\mathrm{d}}\right)-2k\mathrm{sin}\left(3{t}_{1,\mathrm{d}}\right)+k\mathrm{cos}\left(2{t}_{1,\mathrm{d}}\right)\mathrm{sin}\left(2{t}_{1,\mathrm{d}}\right)+k\mathrm{sin}\left(2{t}_{1,\mathrm{d}}\right)\left({\mathrm{cos}\left({t}_{1,d}\right)}^{2}-{\mathrm{sin}\left({t}_{1,\mathrm{d}}\right)}^{2}\right)\right)}^{2}+4{k}^{2}{\left(\frac{{\mathrm{sin}\left(2{t}_{1,d}\right)}^{2}}{2}+\mathrm{cos}\left(3{t}_{1,d}\right)-\mathrm{cos}\left({t}_{1,d}\right)-\frac{\mathrm{cos}\left(2{t}_{1,d}\right)\left(\mathrm{cos}{\left({t}_{1,d}\right)}^{2}-\mathrm{sin}{\left({t}_{1,d}\right)}^{2}\right)}{2}+\frac{1}{2}\right)}^{2} \right)}^\frac{1}{2}=\Delta {e}_{d}\left({t}_{1,d}\right)$$
(18)

with \(k\) being defined as \(k=\frac{{A}^{2}{a}_{y}}{2{\omega }^{2}}\)

To determine the required coasting time \({t}_{c,d}\), the so coasting angle \({\theta }_{c,d}\) needs to be calculated first. It is defined as:

$${\theta }_{c,d}={\theta }_{P\mathrm{3,1},d}-{\theta }_{P\mathrm{3,0}}$$
(19)

Here, \({\theta }_{P\mathrm{3,0}}\) refers to the initial phase 3 position and \({\theta }_{P\mathrm{3,1},d}\) to the initial position of the pnp/npn sequence \(\left({\alpha }_{1,d},\frac{{\beta }_{1,d}}{\sqrt{2cA}}\right)\) according to the coordinate system depicted in Fig. 5. Since the coasting time for a full orbital revolution (\(\theta =2\pi \)) is \({T}_{c,2\pi }=2\pi {\left(\sqrt{2c{A}^{-1}}\omega \right)}^{-1}\) (see Eq. (6)), the respective coasting time \({t}_{c,d}\) for a coasting angle of \({\theta }_{c,d}\) is:

$$ t_{{c,d}} = \frac{{\theta _{{c,d}} }}{{\omega \cdot \sqrt {\frac{{2c}}{A}} }} $$
(20)

Here, since \(\theta \in [\mathrm{0,2}\pi [\) but \(\mathrm{d}\theta /\mathrm{d}t \ge 0\), \({\theta }_{P\mathrm{3,1},d}= {\theta }_{P\mathrm{3,1},d}+\pi \) if \({{\theta }_{P\mathrm{3,1},d}<\theta }_{P\mathrm{3,0}}\).

2.2.2 Original lift-based algorithm

The lift-based phase 3 algorithm also consists of three segments (pnp or npn) in which differential accelerations are commanded, this time, however, in the \(x\)-direction \(({a}_{x})\). The respective times of the controlled segments are in the following referred to as \({t}_{1,l}\), \({t}_{2,l}\) and \({t}_{3,l}\). After the first segment \({t}_{1,l}\), the sign of the acceleration is switched and applied for a duration \({t}_{2,l}\). Then the sign of the acceleration is switched again for \({t}_{3,l}\) after which the origin has been reached a complete rendezvous has been achieved. To fulfill Eq. (14), the individual durations must fulfill the following condition:

$${t}_{1,l}-{t}_{2,l} +{t}_{3,l}=0$$
(21)

The times are again determined by applying a backwards sequence (\(-{t}_{3,l}\)/\(-{t}_{2,l}\)/\({-t}_{1,l}\)) from the origin (\(\mathrm{0,0}\)). Due to the less restrictive condition stated in Eq. (21) compared to Eq. (16) and (17), two time periods have to be determined as \({t}_{1,l}\) is allowed to differ from \({t}_{3,l}\). For a pnp maneuver sequence, applying the backwards maneuver sequence results in the following system of equation:

$$\frac{{\beta }_{P\mathrm{3,0}}}{\sqrt{2\cdot c\cdot A}}=\left(2\cdot \mathrm{sin}\left(\sqrt{\frac{2\cdot c}{A}}\cdot \omega \cdot {t}_{3,l}+2\cdot \sqrt{\frac{2\cdot c}{A}\cdot \omega \cdot {t}_{1,l}}\right)-\mathrm{sin}\left(2\cdot \sqrt{\frac{2\cdot c}{A}}\cdot \omega \cdot {t}_{3,l}+2\cdot \sqrt{\frac{2\cdot c}{A}}\cdot \omega \cdot {t}_{1,l}\right)-2\cdot \mathrm{sin}\left(\sqrt{\frac{2\cdot c}{A}}\cdot \omega \cdot {t}_{1,l}\right)\right)\cdot \frac{A\cdot {a}_{x}}{2\cdot c\cdot {\omega }^{2}}=\frac{\Delta {\beta }_{l}}{\sqrt{2cA}}({t}_{1,l},{t}_{3,l})$$
(22)
$${\alpha }_{P\mathrm{3,0}}=\left(2\cdot \mathrm{cos}\left(\sqrt{\frac{2\cdot c}{A}}\cdot \omega \cdot {t}_{3,l}+2\cdot \sqrt{\frac{2\cdot c}{A}}\cdot \omega \cdot {t}_{1,l}\right)-\mathrm{cos}\left(2\cdot \sqrt{\frac{2\cdot c}{A}}\cdot \omega \cdot {t}_{3,l}+2\cdot \sqrt{\frac{2\cdot c}{A}}\cdot \omega \cdot {t}_{1,l}\right)-2\cdot \mathrm{cos}\left(\sqrt{\frac{2\cdot c}{A}}\cdot \omega \cdot {t}_{1,l}\right)+1\right)\cdot \frac{A\cdot {a}_{x}}{2\cdot c\cdot {\omega }^{2}}=\Delta {\alpha }_{l}({t}_{1,l},{t}_{3,l})$$
(23)

Due to the much weaker symmetry constraints, no coasting segment is required so that the maneuver can be executed immediately.

2.2.3 Verification

Prior to adding any changes, the implementation of the original algorithms has been verified by Walther et al. [17].

3 Feasibility range determination

As stated by Smith et al. [16], the critical phase for the overall maneuver success is phase 3, in which the algorithms inevitably fail if the initial eccentricity \({e}_{P\mathrm{3,0}}\) exceeds a certain range. Consequently, the terminology feasibility range, as it is used throughout this publication, refers to the maximum value of the initial eccentricity of phase 3 \(\Delta {e}_{\mathrm{max}}\) for which the original algorithm leads to a successful rendezvous. As phase 3 can be controlled either via differential lift or drag, two different feasibility ranges need to be distinguished for each maneuver.

The aim of this article is to develop enhanced phase 3 algorithms which are of open-loop type and i.e. for which the maneuver trajectories can be planned prior to the maneuver. As for the original algorithm there exists a maximum value by which the eccentricity can be reduced (the feasibility range \(\Delta {e}_{\mathrm{max}}\)), the general idea of both algorithms is to iteratively reduce the eccentricity \(e\) by the maximum eccentricity reduction per iteration \(\Delta {e}_{\mathrm{max}}\) until \(e<\Delta {e}_{\mathrm{max}}\) holds. Then, the conventional algorithm is applied to reach the origin. To fulfill the requirement of being of open-loop type, the number of iterations required to achieve a successful rendezvous needs to be determinable beforehand. Consequently, a method to determine \(\Delta {e}_{\mathrm{max}}\), which so far can only be determined using Monte Carlo methods, in advance is required.

In this section, the method developed to determine the size of the feasibility range \(\Delta {e}_{\mathrm{max}}\) for differential drag and for differential lift without the need to perform time consuming Monte Carlo simulations is presented and discussed in detail. Since for the subsequent algorithms also the location \({\theta }_{\Delta {e}_{\mathrm{max}}}\) at which the maximum eccentricity reduction \(\Delta {e}_{\mathrm{max}}\) can be achieved needs to be known, a method to determine these location is presented in this section as well.

3.1 Feasibility range using differential drag

3.1.1 The size of the feasibility range \({\Delta e}_{\mathrm{max},d}\)

As described in Sect. 2.2.1, the required time period \({t}_{1,d}\) is calculated via Eq. (18) in which the time period \({t}_{1,d}\) is adjusted so that the resulting eccentricity reduction \(\Delta {e}_{d}({t}_{1,d})\) exactly matches the initial eccentricity \({e}_{P\mathrm{3,0}}\). If this is the case, the current eccentricity \({e}_{P\mathrm{3,0}}\) is completely zeroed out and the maneuver is therefore successful. An example of a successful maneuver can be found in Fig. 6, in which the initial eccentricity \({e}_{P\mathrm{3,0}}\) is plotted in orange and the time dependent part of Eq. (18), namely \(\Delta {e}_{d}({t}_{1,d})\), is plotted over \({t}_{1,d}\) in blue. The respective boundary conditions used in the example case are listed in Table 1.

Fig. 6
figure 6

\(\Delta {e}_{d}\) over \({t}_{d,1}\) (blue) and initial eccen. \({e}_{P\mathrm{3,0},d}\) (orange)

Full size image
Table 1 Boundary conditions used in the example case taken from [15]
Full size table

All intersections between the two curves represent solutions to Eq. (18) and lead to a successful maneuver. However, as the shortest overall maneuver time is desired, the intersection marked with a black star is chosen. This occurs at \({t}_{1,d}=1534 s\). However, Fig. 6 also shows that the time-dependent part of Eq. (18), \(\Delta {e}_{d}({t}_{1,d})\), varies periodically with \({t}_{1,d}\) and has a distinct maximum value \({\Delta e}_{\mathrm{max}, d}\) of \(\mathrm{326,1}\) m for \({t}_{1,{\Delta e}_{\mathrm{max}},d}=1902 s\). This value, which is the maximum possible reduction of the eccentricity for the given boundary conditions, exactly represents the size of the feasibility range for differential drag. Thus, the desired value for \({\Delta e}_{\mathrm{max}, d}\) can be calculated by determining the maximum of Eq. (24).

$${\Delta e}_{d}({t}_{1,d})={\left({\left(2k\mathrm{sin}\left({t}_{1,\mathrm{d}}\right)-2k\mathrm{sin}\left(3{t}_{1,\mathrm{d}}\right)+k\mathrm{cos}\left(2{t}_{1,\mathrm{d}}\right)\mathrm{sin}\left(2{t}_{1,\mathrm{d}}\right)+k\mathrm{sin}\left(2{t}_{1,\mathrm{d}}\right)\left({\mathrm{cos}\left({t}_{1,d}\right)}^{2}-{\mathrm{sin}\left({t}_{1,\mathrm{d}}\right)}^{2}\right)\right)}^{2}+4{k}^{2}{\left(\frac{{\mathrm{sin}\left(2{t}_{1,d}\right)}^{2}}{2}+\mathrm{cos}\left(3{t}_{1,d}\right)-\mathrm{cos}\left({t}_{1,d}\right)-\frac{\mathrm{cos}\left(2{t}_{1,d}\right)\left(\mathrm{cos}{\left({t}_{1,d}\right)}^{2}-\mathrm{sin}{\left({t}_{1,d}\right)}^{2}\right)}{2}+\frac{1}{2}\right)}^{2} \right)}^\frac{1}{2}$$
(24)

Notably, the size is dependent on the available differential acceleration \({a}_{y}\), the SS coefficient \(c\) and the angular velocity of the chief \(\omega \). Throughout this article, the maximum is found using MATLAB’s fminsearch function. A comparison of calculated values and values extracted from Monte Carlo simulations can be found in 0. In addition, thereby not only the maximum value \({\Delta e}_{max, d}\) can be determined but also the respective time \({t}_{1,\Delta {e}_{\mathrm{max}},d}\). This value is required to determine the respective position from which the maximum reduction can be achieved, which is discussed in the next section.

3.1.2 Required positions \({\theta }_{\Delta {e}_{\mathrm{max}},0,d}\) to reach \({\Delta e}_{\mathrm{max},d}\)

The required position to reach \({\Delta e}_{\mathrm{max},d}\) can simply be calculated by applying the pnp-sequence backwards: \(-{t}_{3,\Delta {e}_{\mathrm{max}},d}\)/\(-{t}_{2,\Delta {e}_{\mathrm{max}},d}\)/\(-{t}_{1,\Delta {e}_{\mathrm{max}},d}\). The value for \({t}_{1,\Delta {e}_{\mathrm{max}},d}\) has been determined in the previous section and \({t}_{2,\Delta {e}_{\mathrm{max}},d}\) and \({t}_{3,\Delta {e}_{\mathrm{max}},d}\) can be calculated using Eqs. (16) and (17), respectively. By definition, this results in a state with an eccentricity of \({e}_{\mathrm{max},d}\) and at the desired position \({\theta }_{\Delta {e}_{\mathrm{max}},d,pnp}\). Due to the symmetry of the two different sequences (pnp/npn), the following relation between the two possible positions holds:

$${\theta }_{\Delta {e}_{\mathrm{max}},0,d,npn}={\theta }_{\Delta {e}_{\mathrm{max}},0,d,pnp}+\pi $$
(25)

3.2 Feasibility range using differential lift

3.2.1 The size of the feasibility range \({\Delta e}_{\mathrm{max},l}\)

In Fig. 7, for an exemplary (successful) maneuver the regions in which Eq. (22) are fulfilled are displayed in red, and the regions in which Eq. (23) are fulfilled in blue (equations solved using MATLAB’s fminsearch function).

Fig. 7
figure 7

\({\alpha }_{f,l}({t}_{1,l},{t}_{3,l})=0\) (red) and \({\beta }_{f,l}({t}_{1,l},{t}_{3,l})=0\) (blue). \(\Delta {e}_{l}({t}_{1,l},{t}_{3,l})=0\) at intersections between blue and red lines

Full size image

For the sake of comparability, the boundary conditions noted in Table 1 were employed again. As both equations need to be fulfilled at the same time, all intersections of both curves represent a solution to the system of equations. To reduce the maneuver time, the solution with the shortest overall phase duration is used as the final solution. This is marked as a black cross.

If the maneuver is unsuccessful, Eqs. (22) and (23) cannot be fulfilled at the same time. However, in this case, the required time periods \({t}_{1,\Delta {e}_{\mathrm{max}},l}\) and \({t}_{3,\Delta {e}_{\mathrm{max}},l}\) to achieve a maximum possible reduction in the eccentricity \({\Delta e}_{\mathrm{max},l}\) can be determined. Similar to the drag-based algorithms, this is achieved by only considering the time varying parts of the equations, namely \(\Delta {\alpha }_{l}({t}_{1,l},{t}_{3,l})\) and \(\Delta {\beta }_{l}({t}_{1,l},{t}_{3,l})\), respectively. For a pnp maneuver sequence, these can be calculated via the following equations:

$$ \Delta \alpha _{l} \left( {t_{{1,l}} ,t_{{3,l}} } \right) = \left( {2 \cdot \cos \left( {2 \cdot \omega \cdot t_{{1,l}} \cdot \sqrt {\frac{{2c}}{A}} + \omega \cdot t_{{3,l}} \cdot \sqrt {\frac{{2 \cdot c}}{A}} } \right) - \cos \left( {2 \cdot \omega \cdot t_{{1,l}} \cdot \sqrt {\frac{{2 \cdot c}}{A}} + 2 \cdot \omega \cdot t_{{3,l}} \cdot \sqrt {\frac{{2 \cdot c}}{A}} } \right) - 2 \cdot \cos \left( {\omega \cdot t_{{1,l}} \cdot \sqrt {\frac{{2 \cdot c}}{A}} } \right) + 1} \right) \cdot \frac{{a_{x} \cdot A}}{{2 \cdot c \cdot \omega ^{2} }} $$
(26)
$$ \frac{{\Delta \beta _{l} \left( {t_{{1,l}} ,t_{{3,l}} } \right)}}{{\sqrt {2cA} }} = \left( {2 \cdot \sin \left( {2 \cdot \omega \cdot t_{{1,l}} \cdot \sqrt {\frac{{2c}}{A}} + \omega \cdot t_{{3,l}} \cdot \sqrt {\frac{{2 \cdot c}}{A}} } \right) - \sin \left( {2 \cdot \omega \cdot t_{{1,l}} \cdot \sqrt {\frac{{2 \cdot c}}{A}} + 2 \cdot \omega \cdot t_{{3,l}} \cdot \sqrt {\frac{{2 \cdot c}}{A}} } \right) - 2 \cdot \sin \left( {\omega \cdot t_{{1,l}} \cdot \sqrt {\frac{{2 \cdot c}}{A}} } \right)} \right) \cdot \frac{{a_{x} \cdot A}}{{2 \cdot c \cdot \omega ^{2} }} $$
(27)

To calculate a value for \(\Delta {e}_{l}\) as a function of \({t}_{1,l}\) and \({t}_{3,l}\), the expressions for \(\Delta {\alpha }_{l}({t}_{1,l},{t}_{3,l})\) and \(\Delta {\beta }_{l}({t}_{1,l},{t}_{3,l})\) need to be inserted in the equation of the eccentricity, Eq. (28).

$$\Delta {e}_{l}\left({t}_{1,l},{t}_{3,l}\right)=\sqrt{\Delta {\alpha }_{l}{\left({t}_{1,l},{t}_{3,l}\right)}^{2}+{\left(\frac{\Delta {\beta }_{l}\left({t}_{1,l},{t}_{3,l}\right)}{\sqrt{2cA}}\right)}^{2}}$$
(28)

In Fig. 8, the \(\Delta {e}_{l}\) is plotted as a function of \({t}_{1,l}\) and \({t}_{3,l}\). The global optimum \({\Delta e}_{\mathrm{max},l}\), which represents the size of the feasibility range for differential lift, is plotted as a pink star. For the respective boundary conditions, \({\Delta e}_{\mathrm{max},l}=36.54 m\) for \({t}_{1,{\Delta e}_{\mathrm{max}},l}=1852 s\) and \({t}_{3,{\Delta e}_{\mathrm{max}},l}=1852 s\).

Fig. 8
figure 8

Plot of \(\Delta {e}_{l}({t}_{1,l},{t}_{3,l})\) over \({t}_{1,l}\) and \({t}_{3,l}\) with \({\Delta e}_{\mathrm{max},l}\) indicated in pink

Full size image

Notably, the value of \({\Delta e}_{max,l}\) is again dependent on the available differential acceleration \({a}_{x}\), the SS coefficient \(c\) and the angular velocity of the chief \(\omega \). Again, in addition to the value of \({\Delta e}_{\mathrm{max},l}\), also the respective times \({t}_{1,\Delta {e}_{\mathrm{max}},l}\) and \({t}_{3,\Delta {e}_{\mathrm{max}},l}\) can be determined.

3.2.2 Required positions \({\theta }_{\Delta {e}_{\mathrm{max}},0,l}\) to reach \({\Delta e}_{\mathrm{max},l}\)

The required position \({\theta }_{\Delta {e}_{\mathrm{max}},0,l,pnp}\) to reach \({\Delta e}_{\mathrm{max},l}\) can again be calculated by applying the pnp-sequence backwards: \(-{t}_{3,\Delta {e}_{\mathrm{max}},l}\)/\(-{t}_{2,\Delta {e}_{\mathrm{max}},l}\)/\(-{t}_{1,\Delta {e}_{max},l}\). The values for \({t}_{1,\Delta {e}_{\mathrm{max}},l}\) and \({t}_{3,\Delta {e}_{\mathrm{max}},l}\) have been determined in the previous section and \({t}_{2,\Delta {e}_{\mathrm{max}},l}\) can be calculated using Eq. (21). Due to the symmetry of the two different sequences (pnp/npn), the following relation between the two possible positions holds:

$${\theta }_{\Delta {e}_{\mathrm{max}},0,l,npn}={\theta }_{\Delta {e}_{\mathrm{max}},0,l,pnp}+\pi $$
(29)
3.2.2.1 Verification

The proposed methodology to determine the value of \(\Delta {e}_{\mathrm{max}}\) is validated by comparing the calculated values to values extracted from Monte Carlo results from literature [16, 17]. In addition, supplementary Monte Carlo simulations were performed. The boundary conditions applied in each verification test case are listed in Table 2.

Table 2 Boundary conditions used in the verification test cases
Full size table
3.2.2.2 Drag-based algorithm

In Table 3, the feasibility range for several differential drag based maneuvers determined using Monte Carlo simulations is compared with the values calculated with the presented approach for different boundary conditions. As in the case of Monte Carlo simulations, the sizes had to be extracted from the plots presented in the literature, slight deviations are inevitable.

Table 3 Feasibility range comparison for diff. drag
Full size table
3.2.2.3 Lift-based algorithm

In Table 4, the feasibility range for several differential lift-based maneuvers determined using Monte Carlo simulations are compared with the values calculated with the presented approach for different boundary conditions. Again, some deviations are inevitable. Notably, to describe the feasibility range of differential lift for each Monte Carlo simulation Walther et al. [17] stated two values, a semi-major and a semi-minor axis. This is because the maximum possible eccentricity reduction (\(\Delta {e}_{\mathrm{max},l}\)) can only be reached from the respective locations \({\theta }_{\Delta {e}_{\mathrm{max}},0,l,pnp}\) and \({\theta }_{\Delta {e}_{\mathrm{max}},0,l,npn}\). Thus, these angles determine the orientation of the semi-major axis. As a consequence, the possible eccentricity reduction is reduced for other starting positions. A minimum can be observed at an axis perpendicular to the semi-major axis (for \({\theta }_{\Delta {e}_{\mathrm{max}},0,l,pnp}+\frac{\pi }{2}\) and \({\theta }_{\Delta {e}_{\mathrm{max}},0,l,npn}+\frac{\pi }{2}\)), which is consequently denoted as semi-minor axis. This just described dependency as well as the relation between \({\theta }_{\Delta {e}_{\mathrm{max}},0,l,pnp}\) and \({\theta }_{\Delta {e}_{\mathrm{max}},0,l,npn}\) (stated in Eq. (29)) is clearly visible in Fig. 9, which shows the result of an exemplary Monte Carlo simulation. Here, the semi-major and semi-minor axes are indicated as \(a\) and \(b\), respectively. Since the value calculated with the methodology presented in Sect. 3.2.1 represents the maximum extension of the feasibility range (\(\Delta {e}_{\mathrm{max},l}\)), this consequently refers to the semi-major axis stated by Walther et al. [17].

Table 4 Feasibility range comparison for diff. lift
Full size table
Fig. 9
figure 9

Monte Carlo simulation for determining the feasibility range of the original lift-based algorithm. For clarity, \(\theta_{{\Delta e_{{{\text{max}}}} ,0,l,pnp}}\) is referred to as \(\theta_{pnp}\) and \(\theta_{{\Delta e_{{{\text{max}}}} ,0,l,npn}}\) is referred to as \(\theta_{npn}\) in this case

Full size image

4 Enhanced phase 3 algorithms

Now that the values of \({\Delta }e_{{{\text{max}}}}\) as well as the required initial positions to achieve this reduction \(\theta_{P3,0}\) for both available control options can be determined without the need to perform Monte Carlo simulations (see Sect. 3), all necessary components to design enhanced open-loop-type phase 3 algorithms are available. The general idea of both algorithms is to iteratively reduce the eccentricity \(e\) by \({\Delta }e_{{{\text{max}}}}\) until \(e < {\Delta }e_{{{\text{max}}}}\) holds. Then, the conventional algorithm is applied to reach the origin. In the following, the enhanced algorithms are presented and discussed in detail. Figure 10 shows a flowchart indicating the general structure of the enhanced algorithms.

Fig. 10
figure 10

Flowchart of the enhanced phase 3 algorithms

Full size image

4.1 Enhanced drag-based phase 3 algorithm

4.1.1 Determination of \(n_{{{\text{req}},d}}\)

In a first step, the number of iterations \(n_{{{\text{req}},d}}\) required to perform the maneuver is determined using the following equation:

$$ n_{{{\text{req}},d}} = {\text{ceil}}\left( {\frac{{e_{P3,0} }}{{{\Delta }e_{{{\text{max}},d}} }}} \right). $$
(30)

Here, ceil() indicates that the number is rounded up to the next integer in any case. If the initial conditions are inside the feasible range (\(n_{{{\text{req}},d}} = 1\)), the original phase 3 algorithm, described in Sect. 2.2.1, is executed as it is sufficient to successfully perform the maneuver. If the initial conditions are outside of the feasibility range (\(n_{{{\text{req}}}} > 1\)), the enhanced algorithm is required for a successful maneuver.

4.1.2 Initial coasting period \(t_{{c,{\text{init}},d}}\)

Since the maximum eccentricity reduction \({\Delta }e_{{{\text{max}},d}}\) for the drag-based phase 3 algorithm can only be reached from \(\theta_{P3,0,d,pnp}\) or \(\theta_{P3,0,d,npn}\), the deputy is required to coast from initial position \(\theta_{{\Delta e_{{{\text{max}}}} ,0,d}}\) to the next possible starting position. Whether the initial iteration is of pnp- or npn-type depends on \(\theta_{{\Delta e_{{{\text{max}}}} ,0,d}}\), which is the position at the beginning of phase 3:

$$ {\text{initial iteration }}\left( {{\text{ii}}} \right) = \left\{ {\begin{array}{*{20}c} { \theta_{{\Delta e_{{{\text{max}}}} ,0,d,pnp}} \le \theta_{P3,0} \le \theta_{{\Delta e_{{{\text{max}}}} ,0,d,npn}} : npn} \\ { {\text{else}}:pnp} \\ \end{array} } \right.. $$

The information with which type of maneuver sequence the maneuver is initiated is referred to as \(ii\) in the following. If the initial maneuver sequence is of pnp-type, the respective coasting time \(t_{{c,{\text{init}},d}}\) can be calculated as:

$$ t_{{c,{\text{init}},d,pnp}} = \frac{{\theta _{{\Delta e_{{\max }} ,0,d,pnp}} - \theta _{{P3,0}} }}{{\omega \cdot \sqrt {\frac{{2c}}{A}} }}. $$
(31)

Vice versa, if the first maneuver sequence is of npn-type, the respective coasting time is:

$$ t_{{c,{\text{init}},d,npn}} = \frac{{\theta _{{\Delta e_{{\max }} ,0,d,npn}} - \theta _{{P3,0}} }}{{\omega \cdot \sqrt {\frac{{2c}}{A}} }}. $$
(32)

In both cases, since \(\theta \in \left[ {0,2\pi } \right[\) but \({\text{d}}\theta /{\text{d}}t \ge 0\), \(\theta_{{\Delta e_{{{\text{max}}}} ,0,d}} = \theta_{{\Delta e_{{{\text{max}}}} ,0,d}} + 2\pi\) if \(\theta_{{\Delta e_{{{\text{max}}}} ,0,d}} < \theta_{P3,0}\).

4.1.3 Final positions \(\theta_{{\Delta e_{\max } ,f,d}}\) after a \(\Delta e_{\max ,d} \) reduction

In a next step, the final position after an iteration \(\theta_{{\Delta e_{{{\text{max}}}} ,f,d}}\) for both sequence types (pnp/npn) is determined. Therefore, the final state after a sequence is pre-calculated and from it the respective final position \(\theta_{{\Delta e_{{{\text{max}}}} ,f,d}}\) determined. Due to the symmetry of the two different sequences (pnp/npn), the complementary angle can be calculated via the following equation:

$$ \theta_{{\Delta e_{\max } ,f,d,npn}} = \theta_{{\Delta e_{\max } ,f,d,pnp}} + \pi . $$
(33)

4.1.4 Successive \(\Delta e_{\max ,d}\) reduction

Once one of the required starting angles \(\theta_{{\Delta e_{{{\text{max}}}} ,0,d,pnp}}\) or \(\theta_{{\Delta e_{{{\text{max}}}} ,0,d,npn}}\) is reached, the \(\Delta e_{\max ,d}\)-reduction with the pre-calculated acceleration times \(t_{{1,\Delta e_{\max } ,d}}\), \(t_{{2,\Delta e_{\max } ,d}}\), and \(t_{{3,\Delta e_{\max } ,d}}\) is initiated.

4.1.5 Connecting coasting periods \(t_{c,d}\)

To reach the position from which the next iteration can be initiated, the deputy is required to perform a connecting coasting phase for \(t_{c,d}\). Notably, due to the symmetry of the two sequences, a pnp-type sequence is followed by an npn-type sequence to minimize the required coasting time. Vice versa, a pnp-type sequence follows an npn-type sequence.

Following a pnp-type sequence, the required coasting duration \(t_{c,d,pnp}\) is:

$$ t_{{c,d,pnp}} = \frac{{\theta _{{\Delta e_{{\max }} ,0,d,npn}} - \theta _{{\Delta e_{{\max }} ,0,d,pnp}} }}{{\omega \cdot \sqrt {\frac{{2c}}{A}} }} $$
(34)

Vice versa, following an npn-type sequence, the required coasting duration \(t_{c,d,npn}\) is:

$$ t_{{c,d,npn}} = \frac{{\theta _{{\Delta e_{{\max }} ,0,d,pnp}} - \theta _{{\Delta e_{{\max }} ,0,d,npn}} }}{{\omega \cdot \sqrt {\frac{{2c}}{A}} }} $$
(35)

4.1.6 Final approach

The time periods \(t_{1,d}\), \(t_{2,d}\) and \(t_{3,d}\) for the final approach (\(e < \Delta e_{\max ,d}\)) are calculated using the original drag-based algorithm from Shao et al. [15] presented in Chapter 2. As described in Sect. 4.1.3, two final positions after an \(\Delta e_{\max ,d}\) reduction sequence are possible, namely \(\theta_{{\Delta e_{\max } ,f,d,pnp}}\) or \( \theta_{{\Delta e_{\max } ,f,d,npn}}\). Therefore, by determining the value of the remaining eccentricity \(e_{f,d}\) and whether a pnp or npn-type maneuver sequence was performed prior to the final approach, the initial state \(\left( {\alpha_{f,d} ,\frac{{\beta_{f,d} }}{{\sqrt {2cA} }}} \right)\) can be determined.

To do so, \(e_{f,d}\) needs to be calculated by subtracting the sum of all \(\Delta e_{\max ,d}\) maneuvers from the initial eccentricity \(e_{P3,0}\) first:

$$ e_{f,d} = e_{P3,0} - \Delta e_{\max ,d} \cdot \left( {n_{{{\text{req}},d}} - 1} \right) $$
(36)

Whether the last \(\Delta e_{\max ,d}\) maneuver is of pnp- or npn-type depends on the parity of \(n_{{{\text{req}},d}}\) and the initial iteration. The parity of \(n_{{{\text{req}},d}}\) refers to the following expression:

$$ \begin{gathered} {\text{even}} = \left\{ {2n_{{{\text{req}},d}} :n_{{{\text{req}},d}} \in \mathbb{Z}} \right\} \hfill \\ {\text{odd}} = \left\{ {2n_{{{\text{req}},d}} + 1:n_{{{\text{req}},d}} \in \mathbb{Z}} \right\} \hfill \\ \end{gathered} $$

Using the case distinction listed in Table 5, the initial position of the final approach \(\left( {\alpha_{f,d} , \frac{{\beta_{f,d} }}{{\sqrt {2cA} }}} \right)\) can be determined.

Table 5 Case distinction for determining the position of the deputy before the final (drag-based) approach
Full size table

4.1.7 Example maneuver sequence

Figure 11 shows the \(\left( {a,\frac{\beta }{{\sqrt {2cA} }}} \right)\)-phase plane (left) and the corresponding control pattern (\(a_{y}\), right) of an exemplary drag-based phase 3 maneuver performed with the enhanced algorithm for which one \(\Delta e_{\max ,d}\) reduction step is required before the final approach can be initiated. For the sake of comparability, the boundary conditions from Table 1 were used again. The initial values initial oscillating state vector \(\left( {\alpha_{P3,0} ,\frac{{\beta_{P3,0} }}{{\sqrt {2cA} }}} \right)\) were \(\left( {384, - 228} \right)\) so that the initial in-plane eccentricity \(e_{P3,0}\) was \(446.6 \;{\text{m}}\). The overall required maneuver time for phase 3 is \(t_{P3} = 4.26 h\). The remaining in-plane eccentricity after the maneuver, which serves as a measure of the fidelity of the algorithm, is \(e_{{\text{f}}} = 1.78 \cdot 10^{ - 3} \;{\text{m}}\).

Fig. 11
figure 11

Exemplary enhanced drag-based phase 3 maneuver trajectory (left) and respective control profile (right) for which one \(\Delta e_{\max ,d} \) reduction is required before the final approach can be initiated

Full size image

The maneuver proceeds as follows:

  1. 1.

    Initial coasting for \(t_{{c,{\text{init}},d}}\) until the deputy reaches \(\theta_{{\Delta e_{\max } ,0,d}}\) (orange cross).

  2. 2.

    Npn-type sequence with \(\Delta e_{\max ,d}\) (purple/green/light-blue cross).

  3. 3.

    Final approach (pnp) via the original drag-based algorithm (including an initial coasting phase) (blue/red/yellow cross).

To indicate the capability of the new method, an exemplary maneuver sequence for an increased initial eccentricity \(e_{P3,0}\) of \(1414.2\; {\text{m}}\) in which four successive \(\Delta e_{\max ,d} \) reductions (iterations) are required is shown, too (see Fig. 12). In this case, the overall phase time is \(t_{P3} = 11.51 \;{\text{h}}\). In this case, the remaining in-plane eccentricity after the maneuver, which again serves as a measure of the fidelity of the algorithm, is \(e_{{\text{f}}} = 1.59 \cdot 10^{ - 2} \;{\text{ m}}\).

Fig. 12
figure 12

Exemplary enhanced drag-based phase 3 maneuver trajectory (left) and respective control profile (right) for an increased initial eccentricity \(e_{P3,0}\) of \(1414.2\; {\text{m}}\) in which four \(\Delta e_{\max ,d} \) reductions are required

Full size image

4.2 Enhanced lift-based phase 3 algorithm

The general idea is similar to the drag-based algorithm and so is consequently its structure. Differences are a result of the different characteristic of the \(\Delta e_{\max ,l}\) reduction sequence (see Sect. 3.2.1) and discussed in the following.

4.2.1 Determination of \(n_{{{\text{req}},l}}\)

As with the drag-based algorithm, in a first step the number of iterations \(n_{{{\text{req}},l}}\) required to perform the maneuver is determined using the following equations:

$$ n_{{{\text{req}},l}} = {\text{ceil}}\left( {\frac{{e_{P3,0} }}{{\Delta e_{\max ,l} }}} \right). $$
(37)

Again, ceil() indicates that the number is rounded up. If the initial conditions are inside the feasible range (\(n_{{{\text{req}},l}} = 1\)), the original phase 3 algorithm, described in 0, is executed as it is sufficient to successfully perform the maneuver. If the initial conditions are outside of the feasibility range (\(n_{{{\text{req}},l}} > 1\)), the enhanced algorithm is required for a successful maneuver.

4.2.2 Initial coasting period \(t_{{c,{\text{init}},l}}\)

Since the maximum eccentricity reduction \(\Delta e_{\max ,l}\) for the lift-based phase 3 algorithm can only be reached from \(\theta_{{\Delta e_{\max } ,0,l,pnp}}\) or \(\theta_{{\Delta e_{\max } ,0,l,npn}}\), the deputy is required to coast from initial position \(\theta_{P3,0}\) to the next possible starting position. Whether a pnp- or npn-type sequence must be performed at the initial phase 3 iteration depends on the angle at the beginning of phase 3 \(\theta_{P3,0}\):

$$ {\text{initial iteration}} \left( {ii} \right) = \left\{ {\begin{array}{*{20}c} { \theta_{{\Delta e_{\max } ,0,l,pnp}} \le \theta_{P3,0} \le \theta_{{\Delta e_{\max } ,0,l,npn}} :npn} \\ {{\text{else}}:pnp} \\ \end{array} } \right.. $$

If the first maneuver sequence is of pnp type, the respective coasting time \(t_{{c,{\text{init}},l,pnp}}\) can be calculated as:

$$ t_{{c,{\text{init}},l,pnp}} = \frac{{\theta _{{\Delta e_{{\max }} ,0,l,pnp}} - \theta _{{P3,0}} }}{{\omega \cdot \sqrt {\frac{{2c}}{A}} }}. $$
(38)

Vice versa, if the first maneuver sequence is of npn type, the respective coasting time \(t_{{c,{\text{init}},l,npn}}\) can be calculated as:

$$ t_{{c,init,l,npn}} = \frac{{\theta _{{\Delta e_{{\max }} ,0,l,npn}} - \theta _{{P3,0}} }}{{\omega \cdot \sqrt {\frac{{2c}}{A}} }} . $$
(39)

Again, in both cases \(\theta_{{\Delta e_{\max } ,0,l}} = \theta_{{\Delta e_{\max } ,0,l}} + 2\pi\) if \(\theta_{{\Delta e_{{{\text{max}}}} ,0,l}} < \theta_{P3,0}\).

4.2.3 Final positions \(\theta_{{\Delta e_{\max } ,f,l}}\) after a \(\Delta e_{\max ,l} \) reduction

In a next step, the final position after an iteration \(\theta_{{\Delta e_{\max } ,f,l}}\) is determined for both sequence types (pnp/npn). Therefore, the final state after a sequence is pre-calculated and from it the respective value determined. Due to the symmetry of the two different sequences (pnp/npn), the complementary angle can be calculated via Eq. (40).

$$ \theta_{{\Delta e_{\max } ,f,l,npn}} = \theta_{{\Delta e_{\max } ,f,l,pnp}} + \pi . $$
(40)

4.2.4 Successive \(\Delta e_{\max ,l}\) reduction

Once one of the required starting angles \(\theta_{{\Delta e_{\max } ,0,l,pnp}}\) or \(\theta_{{\Delta e_{\max } ,0,l,npn}}\) is reached, the \(\Delta e_{\max ,l}\)-iteration starts with the pre-calculated acceleration times \(t_{{1,\Delta e_{\max } }}\), \(t_{{2,\Delta e_{\max } }}\), and \(t_{{3,\Delta e_{\max } }}\).

4.2.5 Connecting coasting periods \(t_{c,l}\)

As with the drag-based algorithm, to reach the subsequent position for which the next iteration can be started, the deputy is required to perform a connecting coasting phase for \(t_{c,l}\). Again, due to the symmetry of the two sequences, a pnp-type sequence is followed by an npn-type sequence to minimize the required coasting time.

Following a pnp sequence, the required coasting duration \(t_{c,l,pnp}\) is:

$$ t_{{c,l,pnp}} = \frac{{\theta _{{\Delta e_{{\max }} ,0,l,npn}} - \theta _{{\Delta e_{{\max }} ,f,l,pnp}} }}{{\omega \cdot \sqrt {\frac{{2c}}{A}} }}. $$
(41)

Vice versa, following an npn sequence, the required coasting duration \(t_{c,l,npn}\) is:

$$ t_{{c,l,npn}} = \frac{{\theta _{{\Delta e_{{\max }} ,0,l,pnp}} - \theta _{{\Delta e_{{\max }} ,f,l,npn}} }}{{\omega \cdot \sqrt {\frac{{2c}}{A}} }}. $$
(42)

4.2.6 Final approach

In contrast to the enhanced drag-based algorithm, a coasting phase \(t_{c,l}\) to reach either \(\theta_{{\Delta e_{\max } ,0,l,pnp}}\) or \(\theta_{{\Delta e_{\max } ,0,l,npn}}\) is added prior the final approach as thereby a successful maneuver can be ensured. Otherwise, it would be possible that, even though \(e < \Delta e_{\max ,l}\) holds, the maximum achievable eccentricity reduction from the current location would be too little due to the angular dependency of \(\Delta e_{\max ,l}\) (see Fig. 9). In the drag-based case, a coasting period to the respective location is included in the original algorithm anyways and is therefore not required.

The time periods \(t_{1,l}\), \(t_{2,l}\) and \(t_{3,l}\) for the final approach (\(e < \Delta e_{\max ,l}\)) are calculated with the original lift-based algorithm presented in 0. As listed in 0, there are two possible end positions of the \(\Delta e_{\max ,l}\) maneuver, either \( \theta_{{\Delta e_{\max } ,f,l,pnp}}\) or \(\theta_{{\Delta e_{\max } ,f,l,npn}}\). Therefore, by determining how large the remaining eccentricity \(e_{f,l}\) is and whether a pnp- or npn-type maneuver is performed before the final approach, its initial state \(\left( {\alpha_{f,l} ,\frac{{\beta_{f,l} }}{{\sqrt {2cA} }}} \right)\) can be calculated.

To do so, \(e_{f,l}\) needs to calculate by subtracting the sum of all \(\Delta e_{\max ,l}\) maneuvers from \(e_{P3,0}\) first:

$$ e_{f,l} = e_{P3,0} - \Delta e_{\max ,l} \cdot \left( {n_{{{\text{req}},l}} - 1} \right). $$
(43)

Again, whether the last \(\Delta e_{\max ,l}\) maneuver is of pnp or npn type depends on the parity of \(n_{{{\text{req}},l}}\) and the initial iteration. The parity of \(n_{req,l}\) refers to the following expression:

$$ \begin{gathered} {\text{even}} = \left\{ {2n_{{{\text{req}},l}} :n_{{{\text{req}},l}} \in {\mathbb{Z}}} \right\} \hfill \\ {\text{odd}} = \left\{ {2n_{{{\text{req}},l}} + 1:n_{{{\text{req}},l}} \in {\mathbb{Z}}} \right\}. \hfill \\ \end{gathered} $$

With the following case distinction, the initial position \(\left( {\alpha_{f,l} ,\frac{{\beta_{f,l} }}{{\sqrt {2cA} }}} \right)\) of the final approach can be determined as displayed in Table 6.

Table 6 Case distinction for determining the position of the deputy before the final (lift-based) approach
Full size table

As described in 0, \(\alpha_{f,l}\),\( \frac{{\beta_{f,l} }}{{\sqrt {2cA} }}\) and \(e_{f,l}\) are utilized to calculate and simulate the final approach that will lead the deputy to the origin.

4.2.7 Example maneuver sequences

Figure 13 shows the maneuver trajectory in the \(\left( {a,\frac{\beta }{{\sqrt {2cA} }}} \right)\)-phase plane (left) and the corresponding control pattern (\(a_{x}\), right) of an exemplary lift-based phase 3 maneuver performed with the enhanced algorithm for which one \(\Delta e_{\max ,l}\) reduction step is required before the final approach can be initiated. For the sake of comparability, the boundary conditions from Table 1 were used again. The initial values initial oscillating state vector \(\left( {\alpha_{P3,0} ,\frac{{\beta_{P3,0} }}{{\sqrt {2cA} }}} \right)\) were \(\left( {30, 30} \right)\) so that the initial in-plane eccentricity \(e_{P3,0}\) was \(42.43\;{\text{ m}}\). The overall required maneuver time for phase 3 is \(t_{P3} = 3.38 h\). The remaining in-plane eccentricity after the maneuver, which serves as a measure of the fidelity of the algorithm, is \(e_{{\text{f}}} = 9.47 \cdot 10^{ - 5} {\text{ m}}\).

Fig. 13
figure 13

Exemplary enhanced lift-based phase 3 maneuver trajectory (left) and respective control profile (right) for which one \(\Delta e_{\max ,l} \) reduction is required before the final approach can be initiated

Full size image

The maneuver proceeds as follows:

  1. 1.

    Initial coasting for \(t_{{c,{\text{init}},l}}\) until the deputy reaches \(\theta_{{\Delta e_{{{\text{max}}}} ,0,l,pnp}}\) (red cross).

  2. 2.

    Pnp-type sequence with \(\Delta e_{\max ,l}\) (yellow/purple/green cross).

  3. 3.

    Coasting for \(t_{c,l,pnp}\) to reach \(\theta_{{\Delta e_{\max } ,0,l,pnp}} \) and to ensure a successful maneuver (light-blue cross).

  4. 4.

    Final approach (pnp) via the original lift-based algorithm (red/blue cross).

To indicate the capability of the new method, an exemplary maneuver sequence for an increased initial eccentricity \(e_{P3,0}\) of \(228 m\) in which six successive \(\Delta e_{\max ,l}\) reductions (iterations) are required is shown, too (see Fig. 14). In this case, the overall phase time is \(t_{P3} = 14.82 h\). In this case, the remaining in-plane eccentricity after the maneuver, which again serves as a measure of the fidelity of the algorithm, is \(e_{f} = 3.5 \cdot 10^{ - 3} m\).

Fig. 14
figure 14

Exemplary enhanced lift-based phase 3 maneuver trajectory (left) and respective control profile (right) for an increased initial eccentricity \(e_{P3,0}\) of \(228 m\) in which six \(\Delta e_{\max ,l}\) reductions are required

Full size image

4.3 Critical discussion and foreseen future work

In the following, foreseen future work is presented before the article content is critical discussed.

4.3.1 Magnitudes of the available differential drag and lift accelerations

For the sake of comparability, the values for the available differential drag and lift accelerations used throughout this article are chosen following the values presented in the literature [15] where is generally assumed that the satellites are of low mass and equipped with dedicated large drag and lift plates (see, i.e., Fig. 1). This results in very optimistic values for the available drag and lift accelerations and consequently achievable maneuver times. More realistic analysis based on a formation of two 3U CubeSat’s orbiting at an altitude of 300 km at moderate solar activity with a mass of 3 kg each indicates significantly lower available control authorities of around \(a_{y} = 6.54 \cdot 10^{ - 6} \;{\text{m/s}}^2\) (\(\sim 16.4\%\)) for differential drag [19]. Thus, future analysis of real mission scenarios should be conducted with more realistic boundary conditions as it is currently being performed.

4.3.2 Practicability in a real mission scenario

Due to their underlying assumptions (i.e., the constant density assumption), the developed control sequences are highly simplified and their practicability in a real mission scenario is limited. Nevertheless, the algorithms are a fast and computationally inexpensive option to design suitable reference trajectories or to estimate maneuver times and can thereby complement more sophisticated analysis, as e.g. shown in [8]. An additional assumption which can hardly be achieved in reality is a pure lift- or pure drag-based maneuver (as it is assumed in the control algorithms throughout this article) as this would assume perfectly matching drag or lift values.

4.3.3 Algorithm related future work

To further increase the understanding and the state-of-the-art of the presented algorithms, the following topics are foreseen to be addressed:

  • Analytical determination of the respective times to achieve \(\Delta e_{\max }\) (zero search of the derivation of the functions for \(\Delta e_{d} \left( {t_{1,d} } \right)\) and the \(\Delta e_{l} \left( {t_{1,l} ,t_{3,l} } \right)\) with respect to the respective times).

  • In-depth assessment of the influence of relevant parameters on \(\Delta e_{\max }\) and \(\theta_{{\Delta e_{\max } ,0}}\).

  • Extension of the algorithms for different formation flight scenarios, e.g., formation establishment or formation re-configuration.

  • Development of simultaneous lift and drag controlled maneuver sequences (see discussion in Sect. 4.3.2).

5 Conclusion

A common practice to design simple reference trajectories or to estimate maneuver times is to calculate the respective control patterns using linearized relative motion models and the constant density assumption. As the resulting algorithms are fast and computationally very inexpensive, powerful tools to gain deep insights and to derive general conclusions can be created by applying Monte Carlo methods. However, the state-of-the-art algorithms inevitably failed if the initial conditions of the third phase exceed a certain maximum range, the so-called feasibility range. Options to enlarge the size of the range and therefore to increase the maneuver success were proposed in a CEAS Space Journal contribution in 2019 and shown to be successful in a follow-up article published in the same journal in 2020.

This article builds upon the two preceding articles and presents enhanced phase 3 algorithms for differential lift or drag, respectively. In an iterative manner, the proposed algorithms reduce the current in-plane eccentricity by the maximum possible reduction per repetition \(\Delta e_{\max }\) until a successful rendezvous is accomplished. As this value can only be accomplished from certain conditions in the \(\left( {\alpha ,\frac{\beta }{{\sqrt {2cA} }}} \right)\)-plane, coasting periods between the iterations are required. The respective control times can be calculated beforehand so that the enhanced algorithms are of open-loop nature and render all maneuver which previously had to be defined as unsuccessful due to algorithm limitations successful. To realize the just described approach, a fast and precise method to determine a value for \(\Delta e_{\max }\), which equals the size of the feasibility range and so far could only be determined via Monte-Carlo simulations, had to be developed. In the future, this can be employed to efficiently and precisely assess the influence of relevant boundary conditions on the feasibility range.

In summary, the presented results enhance the current state-of-the-art of simplified trajectory design algorithms by proposing enhanced phase 3 algorithms which solve the problematic related to the feasibility range and ensure the success of the maneuver in any case.