Introduction

Working memory (WM) is generally defined as a set of memory processes that enable the maintenance of information during concurrent processing of other information [1]. The Time-Based Resource Sharing (TBRS) theory [2] assumes that this is achieved by a rapid switching between processing new stimuli and refreshing already encoded information. According to the theory, any information that is not in the focus of attention suffers from time-based decay. Hence, there is a need for frequent refreshing of to-be-maintained information. Due to the central attentional bottleneck [3], though, attention can be devoted to only one central process at a time. Thus, the sharing of attentional resources between processing and refreshing needs to be time-based [2].

Being a general theory of WM, TBRS is not concerned with expertise. However, other theories of WM such as template theory [4] or long-term WM theory (LT-WM) [5] have conceptualized WM as being inherently influenced by expertise. Experts’ WM has been repeatedly found to be better [6] and this advantage is commonly explained with both the concept of chunking [7,8,9] and the rapid access to long-term memory (LTM) [10, 11]. The main idea of chunking is that experts’ memory system detects known structures in processed stimuli and recodes them as single, meaningful units [12].

Besides these theoretical explanations, there is biological evidence for expertise differences in WM. James and colleagues [13] compared gray matter density between participants of three levels of musical expertise. Their analysis revealed that a higher level of expertise is associated with an increase in gray matter density in areas involved in higher-order cognitive processing, including the left inferior frontal gyrus which is involved in working memory processes.

In the context of the TBRS theory, an account of how central WM processes and chunking change with expertise is lacking. The present work addressed this issue by analyzing expertise differences in WM and chunking in the processing of musical note symbols. To this end, we created a musical complex span task. In complex span tasks, memoranda have to be maintained while a secondary distractor task is performed [14]. In the most classical example, the reading span task, numerous sentences have to be read aloud and the last word of each sentence has to be memorized [15]. Analogously, in the present task, single note symbols were presented for later serial recall. In between the presentation of each of these to-be-remembered notes, participants had to perform a short, unknown, notated melody on an electric piano. Hobby musicians and music students completed this task and its procedure was slightly adapted to match the skill level of the two sub-samples.

To manipulate the possibility for chunking, we varied the meaningfulness of the tonal structure of the sequences of to-be-remembered notes. In meaningful sequences, the to-be-remembered notes formed major triads, which can be considered meaningful units in tonal music. In stimuli that were not meaningful, to-be-remembered notes formed arbitrary trichords, i.e., tonal structures that were at odds with the common rules of tonal music. We generally expected that more musically experienced participants would gain an additional benefit in recalling sequences of major triads.

In addition to identifying the interplay of expertise groups and tonal structure conditions, our goal was to uncover the underlying cognitive mechanisms. One method to pursue this goal was to design a computational model that can perform the same experiment as the participants by expressing the involved cognitive processes within a computational framework. This framework was the TBRS*C computational model [16], which is a model of WM supplemented with a chunking mechanism. The TBRS*C model performed the experimental task and it was analyzed which parameter estimates best reflected expertise differences in the human data. This provided insights how WM processes and chunking might change with expertise.

The TBRS*C Computational Model

TBRS*C [16] uses the same functional core as TBRS*, which was developed by Oberauer and Lewandowsky [17] as a computational implementation of the TBRS verbal theory. TBRS* simulates serial recall in complex span tasks. Because recall is serial in such tasks, associations between items and their position in the sequence have to be built and maintained. For instance, if participants are presented with the items A, B, and C, it is supposed that they have to create associations between item A and position 1, item B and position 2, etc. This is described in TBRS* by a Hebbian learning mechanism which has both a cognitive and a computational modeling basis. The Hebbian learning rule [18] describes the modification of neural network connections as a result of the firing of output neurons [19]. More specifically, if cell assemblies, i.e., networks of interconnected neurons that form a functional unit [20], are activated simultaneously, they become associated. The unsupervised learning in neural networks has been described based on this rule [21, 22].

The specific decay/refresh mechanisms in TBRS also have a neural equivalent. Although WM is generally assumed to be biologically implemented by persistent spiking activity, another line of research considers that WM can be explained by short-term synaptic plasticity mediated by increased residual calcium levels [23]. In this kind of model, memory maintenance is directly achieved through short-term synaptic facilitation. However, this facilitation decays over time [24].

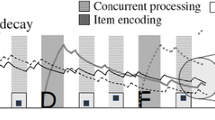
In line with these explanations, TBRS* stores associations between items and positions in a network with two fully interconnected layers, i.e., a position layer and an item layer. Each item is represented by a node in the item layer that is connected with a set of position markers in the position layer. Adjacent positions share a certain proportion P (30% by default) of these markers in order to represent the fact that people are more likely to confound a position with the previous or the next one, but less likely with others. TBRS* reproduces the basic operations of a complex span task, namely encoding, refreshing, distractor processing, and recall. Following the assumptions of the underlying TBRS model, only one of these processes can be performed at a time and all items that are not in the focus of attention suffer from time-based decay. Figure 1 presents the architecture that is the basis of TBRS*.

Fig. 1
figure 1

Model architecture of TBRS*. Upper panel: Simulated time course of a complex span task in which items J, N, H, and F are encoded (light gray areas). Two distractors are processed in between each encoded item (dark gray areas). Free time (white areas) is used to refresh items. Curves represent the total activation value of each item with respect to its position. Lower panel: Connections between position and item units. Each item is represented by a single unit. Each position is represented by several units. Black and white squares represent position coding. For instance, position 1 is coded by units 3, 6, 8, 12, and 13. Positions 1 and 2 share units 3 and 8. Examples of specific processes: (i) item J is encoded and associated with all units of position 1; (ii) item N is encoded and associated with all units of position 2; (iii) all activation values decay during distracting tasks; (iv) during free time, items are retrieved and refreshed for each position in turn; (v) during free time following the second distractor after item H was presented, item H was erroneously retrieved at position 2, instead of N. Then, H was associated with all units of position 2. Figure reproduced from Lemaire and Portrat [25]

Full size image

Table 1 provides an overview of the parameters of the computational model. These parameters will now be explained in detail. Encoding of items is performed by a Hebbian mechanism that strengthens the association between the item node and the markers representing its position. Basically, each connection weight wip between an item i and a position unit p is increased by ∆wip = η.(L-wip) where L is an asymptotic value set to 1/9 because there are 9 position markers coding each position. This way, the total strength of the item-position association that can be reached during encoding is bound to 1. The rate of increase of the association strength is defined as η = 1—e−Rt, i.e., it follows an exponential curve. It is influenced by the time during which the association is strengthened (t) and the parameter R. With increasing R, the association strength increases faster and hence, the maximum is reached more rapidly. So, R affects the time that is needed to encode a memorandum. For example, with the default value R = 6 and a duration of t = 0.5 s, the strength of the association between an item being encoded and its position is η = 0.95 which represents 95% of the maximum value. Actually, to model some variability, it is not the value R which is used but rather the outcome of a random draw from a normal distribution centered at R, with a standard deviation of s (1 by default).

Table 1 Parameters of the TBRS*C computational model
Full size table

Refreshing in TBRS* occurs during any free time, usually right after encoding items or processing distractors. During refreshing, previous positions are considered in turn and for each one, an item is retrieved and the association with its position markers is strengthened, using the same mechanism as during the initial encoding of an item, presented previously, except that the duration is much shorter. As the duration of refreshing Tr is fixed (80 ms by default), though, a larger R does not result in more rapid refreshing, but in a larger activation reached during refreshing.

Retrieval at a given position is performed by selecting the item whose sum of association strengths to the respective position markers is maximal. To mimic retrieval errors, zero-centered Gaussian noise with standard deviation σ (0.02 by default) is added to each sum of activation strengths. More precisely, the selected item is defined by argmaxi(∑p wip + noise) where noise ~ N(0, σ) and wip is the association weight between item i and position p. However, if that best value is lower than a retrieval threshold ϴ (0.05 by default), no item is recalled as if it was forgotten.

Distractor processing is not simulated per se, but its effect is reproduced by applying a decay function to the item-position associations during processing of distractors. The Ta parameter indicates the time used for the attentional capture of a distractor. During that time, all association weights w decay and become wnew = w.e−D.Ta, where D is a decay parameter usually set to 0.5.

Recall in the model involves the retrieval and output of the most activated item associated with the markers representing a given position, following the mechanism presented previously. Once an item i is recalled, its associations with the current position p are suppressed by Hebbian anti-learning (∆wip =  − ηL) in order to minimize repetition of the same item at a subsequent position. Further details of TBRS* mechanisms and parameters are described in the seminal article [17] or in derived models [26].

TBRS*C [16] extended TBRS* with a chunking mechanism which accounts for the fact that humans may recode known sequences of items as single units to increase recall performance. TBRS*C assumes that there is a period right after encoding an item during which long-term memory is searched for the previous sequence of items. If a chunk is successfully recognized, the items are chained and the known group is associated with the position of the first item in the sequence. This is advantageous, as fewer elements need to be refreshed. So, chunking in TBRS*C denotes a process of searching LTM for sequences of encoded items and recoding them; a chunk denotes a known sequence of items in LTM.

For instance, if the letter sequence X-P-D would be presented, the model would search for XPD in LTM and would not recognize a chunk. However, if the next letter would be F, the model would recognize the chunk PDF and would associate it with the position of the first letter of the acronym. Consequently, only one unit (PDF) would have to be refreshed in position two instead of three letters in positions two, three, and four. To search a known sequence in LTM, all its constitutive elements need to be simultaneously present within the focus of attention. Thus, as opposed to TBRS*, TBRS*C has an attentional focus size of up to four elements [27] meaning that up to four items are refreshed in parallel during each refreshing period. The duration Tr is not modified, but the strength is divided by the number of items N that is considered: ∆wip = η.(L-wip)/N. Items are thus refreshed in groups of 4 instead of individually, but the strength of refreshing is 4 times weaker. Actually, N is not always 4 because at the beginning of the task, there are less than 4 items to be refreshed.

Chunking is implemented in the model by two parameters, namely the time invested in searching for known sequences (chunk search duration, cSD) and the likelihood of recognizing an item as a chunk, given it exists in LTM (probability of chunk retrieval, PCR). Both parameters are separate and independent. With reference to the architecture presented previously, cSD represents an additional amount of time right after encoding an item, during which there is no refresh and all association weights decay, exactly like during the attentional capture of a distractor. PCR, however, does not change the time course of processes in the model as it only controls the probability of recognizing the previous sequence of encoded items as a chunk.

In the initial study on TBRS*C, Portrat and colleagues [16] employed a complex span task in which seven letters were presented as memoranda. Between the presentation of memoranda, participants had to complete spatial judgment tasks. Known letter sequences, namely French three-letter acronyms, were either absent or present, starting at the first, third, or fifth serial position. Participants’ recall data was simulated with TBRS*C leading to the conclusion that chunking is “an attentional time-based mechanism that certainly enhances WM performance but also competes with other processes at hand in WM” [16, p. 430].

Expertise Differences in Working Memory Functioning

In the present work, we assumed two expert advantages in WM functioning, namely chunking and rapid access to LTM. These advantages are assumed by other theories of WM, such as LT-WM [5] and template theory [4]. In addition, they are biologically founded on long-term neural plasticity. When someone practices to become an expert, Hebbian learning takes place [20]. As a consequence, functional units of neurons (so-called cell assemblies) form new associations, thereby creating chunks. For example, if the notes C-E-G are repeatedly activated together with the verbal label “C major,” the notes and the label form a functional unit through Hebbian learning. Rapid access to LTM, however, is based on another mechanism: nerve myelination. Myelin is found in the brain’s white matter. It is a white, fatty tissue that encloses axons and increases the speed of the passing nerve impulses [28]. Myelination is a process that persists for the first three decades of human development and is affected by experience [29]. Specifically, piano practice in certain critical developmental periods was found to be associated with plasticity in myelinating tracts [30]. As a consequence of musical training, myelin cells around nerve fibers have been found to increase in size, contributing to the velocity of electrical impulses [13].

Based on these biological mechanisms, the present study sought to unravel expertise differences in WM functioning in greater detail. To this end, we collected data from a complex span task with musical notation. To ensure variation in musical expertise, the task was completed by two sub-samples, namely music students and hobby musicians. The complex span task required the performance of notated melodies at first sight, which is highly demanding for hobby musicians. Thus, the task procedure was slightly adapted to match hobby musicians’ skill level. Using a median split on the general musical sophistication scale of the Gold Musical Sophistication Index [31], both sub-samples were split up in a higher-expertise and a lower-expertise group (threshold for hobby musicians: 69.5; threshold for music students: 85.5).

The complex span task was additionally performed by the TBRS*C computational model. Separately for both sub-samples, we analyzed which parameter values best reflected the differences in task performance between the higher-expertise and the lower-expertise group. The parameters for this analysis were chosen based on the expected expertise differences in WM: the parameters cSD and R were chosen to investigate experts’ rapid access to LTM; the parameter PCR was chosen to investigate experts’ chunking processes. In addition, we were interested if changes in WM and chunking processes would be associated with changes in the way resources were shared between the two task components. We wondered if the same amount of time would be used for the processing of distractors despite changes in the timing of encoding and chunking. Thus, we explored expertise differences in the parameter that represents the time used for the processing of distractors (Ta). In the analysis, we checked which combination of values for these four parameters (cSD, R, PCR, Ta) would provide the best fit to expertise differences in the human data. Due to the difference in the experimental procedure, music students and hobby musicians were not directly contrasted, but higher-expertise hobby musicians were compared to lower-expertise hobby musicians and higher-expertise music students were compared to lower-expertise music students.

Hobby Musicians

Method

Sample

The hobby musician sub-sample (n = 80) was recruited at the University of Mannheim. It contained 53 female and 25 male students with two participants not providing information on their sex. Participation was restricted to students of any subject except music that considered themselves able to perform musical notes on an instrument. Hobby musicians’ mean age was 21.36 years (SD = 2.55; Min = 18; Max = 31) and most of them studied psychology (27) or teacher education (43). All participants either received 5 € or course credit for their participation.

The general musical sophistication scale of the Gold Musical Sophistication Index (Gold-MSI) [31] revealed that the level of musical expertise of hobby musicians was comparable to the Gold-MSI norm sample (norm sample: M = 70.41; SD = 19.94; hobby musicians: M = 69.75; SD = 13.37). From single items of the Gold-MSI, it became apparent that the average hobby musician in the present study had practiced an instrument regularly and daily for 4 to 5 years (Item 32: M = 4.86; SD = 1.81, means and standard deviations refer to the answering scale of the Gold-MSI), had practiced for one hour daily at the height of musical interest (Item 33: M = 3.24; SD = 1.37), and was able to play two musical instruments (Item 37: M = 2.76; SD = 1.05). For all analyses, we created a group of higher-expertise hobby musicians and a group of lower-expertise hobby musicians by performing a median split on the Gold-MSI score with the threshold of 69.5.

Procedure

The general procedure of one trial of the complex span task is presented in Fig. 2. In the task, twelve single quarter note symbols were presented as memoranda. The pitch of these notes had to be recalled at the correct serial position. Between the presentation of these to-be-remembered notes, participants had to perform an unknown, notated melody on an electric piano. In other words, participants saw a single note they had to memorize, then had to perform a notated melody, saw another note they had to memorize, performed another melody, and so on. After the performance of the twelfth melody, the recall task followed. Participants completed four of these trials, i.e., had to complete four recall tasks. The reason for using such a small number of trials was that one trial took about 6 min and the whole experiment in its present form already took about 1 h. Using a larger number of trials probably might have led to fatigue and hence invalid data. Eye tracking and Midi data were recorded during the musical performance. They were used to analyze the association of the number and duration of fixation with the accuracy of performing the melodies [32]. These analyses, however, were unrelated to the present work and hence will not be reported in any further detail.

Fig. 2
figure 2

Procedure of one trial of the complex span task

Full size image

The complex span task started after participants gave informed consent and received instructions. Each of the four experimental trials began with a preparatory phase with three steps: (1) positioning the hand on the piano keyboard, (2) performing a preparatory melody, (3) calibrating the eye tracker. The tones of the melodies that had to be performed were drawn from a set of five adjacent tones. Participants were informed which tones they would have to play in a given trial and how to position their hand on the keyboard to play them. Thus, participants did not have to move their hands on the piano during one trial. Then, a preparatory melody was provided prior to the experimental task. Participants were allowed to play it for as long as they wanted in order to practice the mapping between note symbols and piano keys. The tones of this melody were drawn from the five tones of the given trial, but apart from that, the preparatory melodies did not resemble the experimental melodies in any further aspect. Subsequently, the eye tracker was calibrated and the complex span task started.

The complex span task consisted of two alternating phases: (1) the presentation of memoranda and (2) the performance of melodies (see Table 2, the mapping to TBRS*C processes will be explained below). The former phase comprised the presentation of a fixation cross (2000 ms) and of a single quarter note symbol in treble clef (2500 ms). The latter comprised a two-bar count-in (6856 ms), the musical performance (13,714 ms), and the saving of eye tracking data. During count-in and performance, a digital metronome provided the tempo of 70 beats per minute via speakers. During the count-in, a preview of the first bar of the melody was provided. The whole melody appeared on the screen when the performance started. After each musical performance, the eye tracking data which had been collected during this performance was saved. Saving times varied marginally (M = 6124 ms; SD = 390 ms). In one trial of the task, the procedure depicted in Table 2 was repeated twelve times until participants had to recall all memoranda and write them in the correct serial order on a sheet of paper with an empty staff.

Table 2. The phases of the musical complex span task and how they were mapped on TBRS*C processes
Full size table

Prior to the first experimental trial, participants performed a warm-up trial. It was similar to the experimental trials. However, only three instead of twelve notes had to be recalled and there were some additional instructions (“memorize the following note,” “play the following melody”) prior to each stimulus. The purpose of this warm-up was that participants could get used to the experimental procedure and that any misunderstandings could be clarified prior to data collection.

In the end of the experiment, participants completed the global scale of the Gold-MSI [31] termed general musical sophistication and answered questions on demographics. The experimental procedure was in full agreement with APA’s Ethical Principles of Psychologists and Code of Conduct [33] and with German data privacy regulations. Footnote 1

Design and Material

The design of the experiment was defined by the between-participants factor expertise group (higher-expertise vs. lower-expertise hobby musicians) and the within-participants factor tonal structure (major triads vs. arbitrary trichords). Sequences of memoranda consisted of four three-note melodic cells. Depending on the level of the factor tonal structure, these cells were either major triads or arbitrary trichords. Major triads can be considered meaningful tonal structures in western music. They consist of a base note called root (e.g., C) and two further notes that have a fixed distance of four and seven semitones to the root (e.g., E and G). The name of a specific major triad is defined by its root (e.g., C major triad). Arbitrary trichords in the present study were defined as consisting of a root note followed by two notes that had a distance of eight and nine semitones to it (e.g., C, G#, A). We assumed that major triads would be beneficial for chunking processes. Participants performed two trials in each condition and were not informed about the regularities within the sequences of notes. The order of trials was randomized. Table 3 shows the twelve memoranda of the four trials.

Table 3. Each staff shows the twelve to-be-remembered notes that were presented successively in one trial of the complex span task
Full size table

To select the memoranda, the roots of each triad, i.e., the notes at positions one, four, seven, and ten, were randomly selected from the notes between C4 and Eb5. As the three-note cells in both conditions had a fixed structure, the remaining notes were derived based on the root notes and experimental conditions. The melodies that had to be performed between the presentation of the memoranda each consisted of four bars, with three notes in each bar (see Fig. 3). They contained only eighth and quarter notes and rests. They were created by arranging four one-bar rhythmic phrases in a random order and assigning a pitch to each note that was randomly drawn from a set of five adjacent pitches from the C major scale. All melodies had a similar structure, which guaranteed that the amount and rate of information that had to be processed was constant across all melodies. Simultaneously, as the order of rhythmic phrases and pitches was varied randomly, it was impossible for participants to anticipate how the melody would progress. Thus, they were forced to process the notes.

Fig. 3
figure 3

Two examples of the notated melodies which participants had to perform between the presentation of to-be-remembered notes

Full size image

Note images were created with the program Forte 7 Basic (https://www.fortenotation.com/en/) and then altered with the graphic-editing software Gimp (https://www.gimp.org/). To create the images containing the to-be-remembered notes, the indication of meter was removed, and a single quarter note symbol (0.3 × 1.2 cm) was positioned in the center of a short staff (6.0 × 1.3 cm) with a treble clef symbol. To-be-remembered notes as well as distractor melodies (24.0 × 0.6 cm) were positioned in the center of a white image (49.92 × 28.08 cm, 1920 × 1080 pixels, 60 cm viewing distance). The experiment was programmed with the software ePrime (https://pstnet.com/products/e-prime/); responses for the recall task and for the questionnaires were indicated on a sheet of paper.

Analyses

To obtain a measure of recall accuracy, the names of the note symbols that participants wrote as their response were transferred manually to a spreadsheet and then recoded as correct (1) or wrong (0) for each serial position. Only notes that were recalled at the correct serial position were judged as correctly recalled. In addition, a melodic cell (i.e., a major triad or an arbitrary trichord) was defined as being recalled correctly if its three notes were recalled correctly. The Midi data of the musical performance was analyzed with the algorithm MidiAnalyze [32] to derive how accurately the distractor melodies were performed.

In the following, we will first present descriptive plots and then results of a Bayesian mixed logistic regression model in which recall accuracy (0/1) was predicted by serial position and an interaction of expertise group (higher-expertise vs. lower-expertise) and tonal structure (major triads vs. arbitrary trichords). This inferential analysis provided insights into the data structure that was the basis for the TBRS*C simulations. Generally, TBRS*C simulations provide serial position accuracies, i.e., mean recall accuracies per serial position. In the present study, simulations were performed separately for expertise groups and experimental conditions. Thus, to interpret the simulations correctly, it is important to understand how recall accuracy varied with serial position, expertise group, and tonal structure.

Prior to analysis, six hobby musicians were excluded as they either had a very low recall accuracy of below 5% or did not adhere to experimental instructions. Experimental materials, data sets, and analysis code of this study can be accessed via https://doi.org/10.17605/OSF.IO/6UKEV.

Results

Figure 4 shows mean values by group and condition for the proportion of correctly recalled notes, of correctly recalled melodic cells, and of correctly performed distractor notes. The left plot shows that recall was more accurate in the higher-expertise group and in the major triads condition; the advantage in the major triads condition was larger in the higher-expertise group.

Fig. 4
figure 4

Descriptive data (means and standard errors) of hobby musicians’ proportion of correctly recalled notes, correctly recalled melodic cells, and correctly performed distractor notes by expertise group and condition

Full size image

To test this pattern statistically, we performed a Bayesian mixed logistic regression. The model was created in Stan (http://mc-stan.org/), accessed via the R package brms [34]. Recall accuracy (0/1) was predicted by serial position and by an interaction of expertise group (higher-expertise vs. lower-expertise) and tonal structure (major triads vs. arbitrary trichords). We implemented a full random structure, i.e., the effect of all predictors as well as the intercept varied across participants. This controlled for any differences between participants that were not accounted for by the predictors, such as domain-general WM capacity. The predictor serial position was an integer variable with values from zero to eleven. Thus, the intercept in the model represented the expected log-odds of the recall accuracy of a lower-expertise hobby musician in the major triads condition at the first serial position. Leave-one-out (loo) analyses were performed but revealed no influential data points.

We used highly informative priors, which were defined a priori based on the expected pattern of results using the conditional means prior approach [35]. Table 4 shows priors and posterior distributions of the regression coefficients. The main effect of tonal structure (posterior mean regression coefficient: 0.71; 95% credibility interval: [0.35, 1.09]) and the interaction of expertise group and tonal structure (posterior mean regression coefficient: 0.63; 95% credibility interval: [0.09, 1.17]) were most pronounced; the main effect of expertise group was of marginal extent (posterior mean regression coefficient: 0.41; 95% credibility interval: [−0.09, 0.91]). To clarify the pattern of interaction, Fig. 5 provides a conditional effects plot. It shows the predicted interaction of expertise group and tonal structure on the accuracy scale for the recall of the sixth note. The sixth note was chosen as it is in the center of the sequence of memoranda, i.e., it might neither be affected by recency nor by primacy effects [36]. The pattern of interaction was as expected: the difference in recall accuracy between sequences of major triads and sequences of arbitrary trichords was larger in the higher-expertise group. This pattern of effects did not change using weakly informative priors.

Table 4 Priors and posterior distribution of regression coefficients of the Bayesian mixed logistic regression for the hobby musician sub-sample
Full size table
Fig. 5
figure 5

Prediction of the Bayesian regression model regarding the interacting effect of tonal structure and expertise group on hobby musicians’ recall accuracy at the sixth serial position

Full size image

Moreover, another regression analysis revealed that the accuracy of performing distractor notes (right panel of Fig. 4) did not differ by group, condition, or their interaction. Using these predictors in a mixed linear model with the package lme4 [37] did not increase the fit to the data compared to a null model without any predictors (χ2 (3) = 4.38; p = 0.22).

TBRS*C Simulations

Serial recall in the musical complex span task was then simulated with TBRS*C to investigate expertise differences in WM and in chunking processes. Table 2 depicts how the different phases of the experimental task were mapped on TBRS*C processes. The number of memoranda was set to twelve, as participants had to recall twelve notes in each of the four trials. From the second repetition onwards, the presentation of the fixation cross was simulated as being used for refreshing already encoded notes. The time span in which the to-be-remembered note was presented was modeled as being used first for the encoding of the currently presented note, then for chunking, and for the refreshing of already encoded notes. However, during the encoding of the first two notes, chunking was not initiated, as chunks consisted of three notes. The duration of encoding the currently presented note depended on the value of the R parameter (6 at default, which corresponds to 500 ms). During chunking, the simulation searched in long-term memory for a chunk consisting of the last three notes. Long-term memory was defined to contain major triads, i.e., it was only possible that the simulation recognizes a chunk in sequences of major triads. Refreshing took place during any free time prior to the distractor task.

The distractor task, i.e., the performance of the notated melodies, started with a two-bar count-in. During this count-in, the first bar of the melody was presented. After the count-in, the four-bar musical performance started. Figure 6 shows how the distractor task was modeled in TBRS*C. Both the preview and the performance were modeled as alternating processing distractor notes and refreshing to-be-remembered notes. Ta indicated the time used to process a distractor note. Any free between the processing of subsequent distractor notes was modeled as being used for refreshing. This means that the preview and the musical performance were identical in the simulations. This approach was based on the assumption that, to prepare the performance, participants would process the distractor notes during the preview in a comparable manner as while playing them. In summary, as each bar contained three distractor notes and as participants read six bars (two-bar preview, four-bar performance), the musical performance was modeled as processing eighteen distractor notes interspersed with refreshing the to-be-remembered notes. In the end of the distractor task, there was a short time interval in which the eye tracking data had to be saved. This time interval was modeled as being used for refreshing.

Fig. 6
figure 6

Schematic representation of the way in which the performance of the distractor melody was simulated in TBRS*C

Full size image

TBRS*C simulations were performed on higher-expertise and lower-expertise hobby musicians independently. Moreover, the simulation of the data was performed in two steps: First, only the data of the arbitrary trichords condition was simulated to obtain a baseline of the parameters Ta, R, and cSD. Second, using these initial parameter estimates, the data of the major triads condition was used to estimate PCR.

This two-step procedure was based on the assumption that the memory system cannot know beforehand if it would recognize a chunk in a certain sequence of memoranda. Hence, chunking is initiated in the arbitrary trichords condition as well. This means that all parameters except for the probability of chunk retrieval (PCR) are the same in both conditions. The PCR parameter, however, can only be estimated if it is possible to recognize chunks, i.e., in the major triads condition.

Table 5 shows the details of this two-step analysis as well as the results. The column “Values” indicates the parameter values that were considered in the analysis. If initial simulations showed that the best-fitting value was one of the extremes of the tested values, additional smaller or larger values were included. We performed a 3000-run simulation with each combination of these values and computed the root mean square error (RMSE) to investigate the fit between the simulated and the human data for each serial position. The TBRS* basic parameters were set to the default values reported in Oberauer and Lewandowsky [17]: P = 0.3; τE = 0.95; s = 1; D = 0.5; Tr = 0.08; θ = 0.1; σ = 0.02. The column “Optimum” in Table 5 indicates the combination of parameter values for which the best fit was obtained.

Table 5 Results of TBRS*C simulations for hobby musicians. A 3000-run simulation was performed for each combination of parameter values. The optimum was the combination of parameter values with the best fit to the experimental data
Full size table

In the simulation of the arbitrary trichords condition, the best fit was obtained with parameters that characterized higher-expertise hobby musicians by a shorter chunk search duration (cSD = 800 ms), a stronger encoding (R = 8), and a longer time of attentional capture of distractor notes (Ta = 600 ms; RMSE = 0.070) compared to lower-expertise hobby musicians (cSD = 1,200 ms; R = 6; Ta = 400 ms; RMSE = 0.091). Using these values, the simulation of the major triads condition suggested that the probability of recognizing a chunk was larger for higher-expertise hobby musicians (PCR = 50%; RMSE = 0.061) than for lower-expertise hobby musicians (PCR = 30%; RMSE = 0.076).

Following these analyses, we were interested if chunking in the simulations was beneficial for recall even though chunks were recognized only with 30 to 50% chance. Thus, we performed a “no chunking” simulation in which cSD and PCR were set to zero and all other parameters were kept constant. Figure 7 shows serial position curves of human and simulated data, separately for expertise groups and tonal structure conditions. The curves of the “no chunking” simulation in the top plots suggest that chunking indeed was beneficial for both expertise groups.

Fig. 7
figure 7

Mean recall accuracy per serial position for simulated and human data of hobby musicians. noChunking denotes a simulation with cSD = 0 and PCR = 0

Full size image

Music Students

Method

Sample

Music students (n = 75) were recruited at the Mannheim University of Music and Performing Arts. Thirty-four participants indicated to be male, 37 indicated to be female, and 4 did not make an indication concerning their sex. The mean age was 23.15 years (Min = 18; Max = 54; SD = 4.67; 3 missing). The prevalent study subjects were Bachelor of Music Education (27) and Bachelor (23) or Master (6) of Music. The mean Gold-MSI musical sophistication score was 84.61 (SD = 7.04), which is nearly one standard deviation above the norm sample reported by Schaal and colleagues [31]. The typical music student had practiced an instrument regularly and daily for 10 years (Item 32: M = 6.8; SD = 0.46), had practiced for four hours daily at the height of musical interest (Item 33: M = 5.85; SD = 1.15), and was able to perform three different musical instruments (Item 37: M = 4.08; SD = 1.17). The sample was divided in a higher-expertise and a lower-expertise group based on a median split of the Gold-MSI score with the threshold of 85.5.

Procedure

The procedure used for the music student sub-sample differed in three aspects from the procedure used for hobby musicians. First, for music students, the preparatory phase prior to each trial did not involve a preparatory melody as it was assumed that they would know the mapping of piano keys to musical notes. Second, and most importantly, the count-in of the musical performance during the complex span task differed. For music students, the first bar of the notated melody was only visible during the second half of the count-in. Third, as this shorter preview resulted in a shorter time of eye tracking, eye tracking data saving took less time for the music students (M = 4,425.09 ms; SD = 143.12). So, in this experiment, the “count-in” phase in Table 2 consisted of a “getting ready” phase (3428 ms) in which the metronome provided the beat and an empty staff was visible, and a “preview” phase (3428 ms) in which the first bar of the melody was presented. This shorter preview made the task more difficult for the music students.

Design, Material, and Analyses

Design, material, and analyses were identical to the ones used for the hobby musician sub-sample. No music students were excluded prior to analyses.

Results

Figure 8 shows means and standard errors of the proportion of correctly recalled notes, of correctly recalled melodic cells, and of correctly performed distractor notes. The accuracy of the recall of notes and melodic cells varied strongly with tonal structure. The proportion of correctly recalled melodic cells was nearly twice as large in the major triads condition compared to the arbitrary trichord condition.

Fig. 8
figure 8

Descriptive data (means and standard errors) of music students’ proportion of correctly recalled notes, correctly recalled melodic cells, and correctly performed distractor notes by group and condition

Full size image

While there was an advantage in the major triads condition compared to the arbitrary trichords condition, this advantage apparently did not vary between higher-expertise and lower-expertise music students. In addition, the plot shows a tendency for an unexpected main effect of expertise group, with the recall accuracy in the higher-expertise group being slightly lower.

To test the significance of this pattern of effects, we calculated a mixed Bayesian regression model in the same manner as for the hobby musician sub-sample. Table 6 shows priors and posterior distributions of the regression coefficients for this model. These results indicate a pronounced positive effect of tonal structure (posterior mean regression coefficient: 0.96; 95% credibility interval: [0.26, 1.64]) with more accurate recall in the major triads than in the arbitrary trichords condition, and a less pronounced negative effect of serial position (posterior mean regression coefficient: −0.16; 95% credibility interval: [−0.20, −0.12]). The model provided no evidence of a main effect of expertise group (posterior mean regression coefficient: 0.23; 95% credibility interval: [−0.44, 0.89]) or of an interaction of expertise group and tonal structure (posterior mean regression coefficient: 0.48; 95% credibility interval: [−0.51, 1.47]). Parameter estimates changed when using uninformative priors, but the overall pattern of effects stayed the same.

Table 6 Priors and posterior distribution of regression coefficients of the Bayesian mixed logistic regression model for the music student sub-sample
Full size table

TBRS*C Simulations

TBRS*C simulations for music students were adapted to the experimental procedure. As explained above, when count-in started, music students heard the metronome and saw an empty staff. This phase was simulated as being used for refreshing to-be-remembered notes. Then, there was a preview of the first bar of the melody and the four-bar musical performance. As each bar contained three notes, the preview (1 bar) and the musical performance (4 bars) were modeled as the processing of 15 distractor notes interspersed with refreshing (cf. Figure 6). In addition, the eye tracking data saving, which was modeled as being used for refreshing to-be-remembered notes, was implemented with a duration of 4425 ms. All other aspects of the TBRS*C simulations were identical to the experiment involving hobby musicians.

Table 7 shows the results of the simulations for these two groups. Overall, parameter estimates that provided the best fit characterized music students as encoding memoranda strongly (R = 8), recognizing chunks with a 100% probability (PCR = 1), and requiring only 100 ms to process distractor notes (Ta = 100 ms). It should be noted that 100 ms is the smallest possible value for the Ta parameter and 1 is the largest possible value for the PCR parameter. Hence, no smaller Ta values and no larger PCR values were included in the exploratory analysis.

Table 7 TBRS*C results for music students. A 3000-run simulation was performed for each combination of parameter values. The optimum was the combination of parameter values with the best fit to the experimental data
Full size table

The only difference in parameter estimates between the expertise groups was that higher-expertise music students invested more time to search for chunks (cSD = 800 ms) than lower-expertise music students (cSD = 600 ms; RMSEarbitrary trichords/lower-expertise = 0.087; RMSEarbitrary trichords/higher-expertise = 0.081; RMSEmajor triads/lower-expertise = 0.112; RMSEmajor triads/higher-expertise = 0.090). Figure 9 shows serial position curves of human and simulated data.

Fig. 9
figure 9

Mean recall accuracy per serial position for simulated and human data of music students

Full size image

Discussion

The present study aimed to provide insights into expertise differences in WM and chunking processes in the context of the Time-Based Resource Sharing model [2]. These insights were provided by simulating the basic cognitive processes necessary for hobby musicians and music students to perform a serial recall task with the TBRS*C computational model [16]. It was analyzed which parameter values would best reflect differences between the higher-expertise and the lower-expertise group within both sub-samples.

The experiment involved a musical complex span task in which twelve single note symbols were presented successively for serial recall of pitch. The presentation of these to-be-remembered notes was interspersed with a distractor task, namely the performance of an unknown, notated melody on an electric piano. We varied within-participants if sequences of to-be-remembered notes formed major triads or arbitrary trichords. We expected that major triads would support chunking, as they can be considered meaningful tonal structures in western music. Accordingly, we expected that sequences of major triads would be recalled more accurately than sequences of arbitrary trichords and that this advantage would be more pronounced in higher-expertise groups.

Analysis of the human data with regression models provided two main insights. First, as expected, hobby musicians’ recall was more accurate in the major triads condition than in the arbitrary trichords condition and this effect was more pronounced in the higher-expertise group. Second, music students’ recall was more accurate in the major triads condition than in the arbitrary trichords condition but did not differ between expertise groups. To go one step further and highlight differences in the underlying cognitive processes, the serial recall task was performed by the TBRS*C computational model [16]. Based on theories of expert memory, such as template theory [4] or LT-WM theory [5] and based on biological findings on long-term chunk formation by Hebbian learning [21] and nerve myelination [13], we assumed that experts’ cognitive advantages result from chunking as well as from their ability to rapidly access information in LTM. Accordingly, the TBRS*C parameters that represent the probability of chunk recognition (PCR) and the speed of accessing LTM (R, cSD) were fit to the human data of the higher-expertise and lower-expertise groups separately for the hobby musician and the music student sub-sample. In addition, we explored if the expertise differences in the timing of encoding and chunking processes would be associated with differences in the sharing of resources between the two task components. Hence, the parameter that represents the time used for the processing of distractors (Ta) was also fit to the human data of the higher-expertise and lower-expertise groups.

In the simulations, hobby musicians searched chunks for 800 to 1200 ms, recognized chunks with a 30 to 50% chance, encoded to-be-remembered notes for 375 to 500 ms, and processed distractor notes for 400 to 600 ms. With respect to expertise differences, simulations indicated that higher-expertise hobby musicians might have encoded to-be-remembered notes more rapidly, might have invested less time in chunk search, and might have been more likely to recognize chunks compared to lower-expertise hobby musicians. This is in line with the notion that expertise supports both chunking [7-9] and the rapid access of information in LTM [10, 11]. Moreover, the present simulations suggested that lower-expertise hobby musicians might have used less time to process distractor notes than higher-expertise hobby musicians. This might have provided them with additional time for refreshing to-be-remembered notes, compensating inefficient encoding and chunking.

Music students in the present simulations were characterized by searching chunks for 600 to 800 ms, by recognizing chunks with a 100% chance, by encoding to-be-remembered notes for 375 ms, and by processing distractor notes for 100 ms. Expertise differences in parameter estimates for music students only concerned the chunk search duration: higher-expertise music students were estimated to have invested 200 ms more in chunk search than lower-expertise music students. However, the regression analysis showed no evidence for an effect of expertise group on music students’ recall accuracy. Thus, the difference in the chunk search duration between expertise groups in the simulations might reflect random variation in recall accuracy across the expertise groups.

Expertise in the Context of the Time-Based Resource Sharing Model

The present simulations suggested that in the context of the Time-Based Resource Sharing model [2], expertise can be conceptualized by (1) a faster encoding of memoranda, (2) a shorter duration of chunk search, and (3) a more reliable recognition of chunks. This can be concluded from differences between higher-expertise and lower-expertise hobby musicians in the parameters R (strength of encoding memoranda), cSD (chunk search duration), and PCR (probability of chunk retrieval), respectively. As such, this finding is in line with theories of expert memory [4, 10] that also assume that experts’ advantage is based both on chunking and the rapid access to information in LTM. However, the present study provided novel insights on the way in which chunking and rapid LTM access are beneficial. The rapid LTM access leads to an increase in the time available to refresh memoranda. The larger chance of recognizing chunks leads to an increase in the efficacy of refreshing. If a chunk is recognized successfully, multiple memoranda can subsequently be refreshed as a single unit. This saves time that can be used for refreshing other chunks or single memoranda. So, if chunking is successful, the association of items and position markers after a period of refreshing is stronger than if chunking fails.

Moreover, in the hobby musician sub-sample, expertise differences in WM and chunking processes apparently were associated with changes in the way in which resources were shared between the tasks. The estimates for the Ta parameter suggest that lower-expertise hobby musicians might have used less time for the processing of distractors. Framed differently, they might have used more time for refreshing during the distractor task. This might be interpreted as compensation for less efficient WM processes. If, due to unsuccessful chunking, items are rather weakly associated with position markers, participants might devote less time to distractor processing to gain additional opportunities to refresh memoranda.

There are, however, two issues that limit the scope of this finding. First, our distractor task and our way of estimating Ta were rather original. Commonly, very simple distractor tasks are used for TBRS*C simulations and Ta is estimated based on measured reaction times. Thus, the validity of estimating Ta by fitting simulated data to human data first needs to be established by additional research. Second, the accuracy in the distractor task is commonly restricted to a rather high level by excluding inaccurate trials. Due to the demanding nature of the distractor task in the present study, we refrained from applying a strict criterion on the accuracy of distractor processing, as this would have led to a large loss of data. Consequently, one might argue that expertise differences in the Ta parameter might indeed result from differences in the accuracy of performing distractor notes. However, our analyses showed that hobby musicians’ accuracy of performing distractor notes was constant across expertise groups. In addition, it is unclear how the time used to process distractor notes and the accuracy of their performance was related. Intuitively, it might be assumed that a longer processing time is associated with a more accurate performance. As musical performance is strictly timed, though, the opposite might be true. A short processing might be associated with a more accurate performance as it facilitates the maintenance of the musical timing. Thus, it is unclear if the accuracy of performing distractor notes is actually relevant for the Ta estimate.

Despite these limitations, it is an empirical fact that the model fit was optimal when Ta differed between expertise groups in such a way that lower-expertise hobby musicians used less time for distractor processing than higher-expertise hobby musicians. To test the assumption that the time used for distractor processing is related to the strength of item-position associations, future studies might experimentally vary the length of refresh episodes prior to the distractor task. If the distractor task starts right after a memorandum is encoded, the association of the previous memoranda with their respective position markers should be weaker than if there is time to refresh prior to the distractor task.

In contrast to the results of hobby musicians, the theoretical implications for music students’ results were less clear. Two aspects need to be discussed in greater detail, namely (1) why simulations suggested that higher-expertise music students invested more time in chunk search than lower-expertise music students and (2) why there were no expertise differences in other parameters.

Concerning the former, we argue that the difference in chunk search duration between higher-expertise and lower-expertise music students was not meaningful as it probably reflected random variation of recall accuracy across expertise groups. The regression analysis showed that the difference in recall accuracy between higher-expertise and lower-expertise music students was not statistically significant. The simulations, though, cannot differentiate between differences that are statistically significant and those that are not. It adapts to any difference between groups.

But why was the marginal difference in recall accuracy between the expertise groups reflected in the cSD parameter and not in some other parameter? The chance of recognizing chunks (PCR) and the time used for processing distractor notes (Ta) were at maximally efficient values for all music students. So, R and cSD were the only possible candidates for creating differences within the music student sub-sample. As R affects both encoding and refreshing, even small changes in R might lead to rather pronounced changes in the recall accuracy. Thus, this parameter might not have been suited to account for the rather small difference in recall accuracy between higher-expertise and lower-expertise music students.

It becomes clear that one drawback of TBRS*C is that it simulates the mean serial position accuracy across groups. When groups are compared, the simulation might indicate differences between groups that merely reflect random variation. As described by Farrell and Lewandowsky [38], one way of handling this problem is by simulating individual participants instead of groups. This leads to distributions of model parameters that can be inferentially tested for differences between groups. Another way of handling this problem is to complement TBRS*C simulations with regression models that analyze the data structure that underlies the simulations, as in the present study. This helps with the interpretation of simulation results as it allows identifying cases in which the simulation reflects group differences that are not statistically significant.

Concerning the finding that there were no differences in other parameters between expertise groups, we argue that there are three potential reasons for this: a ceiling effect, the homogeneity of the music student sub-sample, and the lacking selectivity of the Gold-MSI for extreme values. In the major triads condition, more than 50% of the music students had a recall accuracy of 100%. These participants were equally distributed across the expertise groups, i.e., half of the higher-expertise and half of the lower-expertise music students recalled all sequences of major triads perfectly. This ceiling effect might have obscured the true difference between expertise groups [39], resulting in marginal group differences in recall accuracy and, in turn, similar TBRS*C parameter estimates.

Moreover, the standard deviation of the Gold-MSI score suggests that the music student sub-sample lacked variation in musical expertise. Overall, participants in this sub-sample were on a similar level of musical expertise. Lastly, the selectivity of the Gold-MSI score might decrease for extreme values. The questionnaire might not be suited to differentiate between a highly experienced and a very highly experienced person. Therefore, the categorization of music students as either lower-expertise or higher-expertise might not have been meaningful.

Future studies might avoid ceiling effects in two ways. First, different tonal structures might be used. As reflected in the likelihood of chunk recognition of 100%, major triads might have been too easy to recognize for music students. Other tonal structures that are more complex and less common might be recognized only by highly experienced music students. Second, future studies might employ computerized adaptive testing [40]. This method gradually adapts the difficulty of a task to the participant’s ability level. The difficulty of the next trial in an experiment is selected based on the accuracy in the recently completed trials. In a complex span task, this would mean that the list length of a trial is adapted based on the recall accuracy of the previous trials. When a trial is completed with perfect accuracy, the number of memoranda in the following trials would increase up until a point where the recall accuracy is no longer perfect. This method avoids ceiling effects and thereby allows to accurately measure differences between participants even in groups that are very experienced.

Lastly, it might appear as if interference between the to-be-remembered notes and the to-be-performed notes might pose a problem for our findings. The level of interference was constant across expertise groups and tonal structure conditions, though. Hence, interference cannot explain the differences we found between these factors. Nevertheless, the present findings should be replicated by future studies with a distractor task that is not domain specific.

Implications for Chunking

In addition to the conceptualization of expertise within the Time-Based Resource Sharing model, the present results provided insights into chunking mechanisms. It became apparent that chunking is a universal process that is not restricted to experts. The simulation of hobby musicians suggests that they might have invested a considerable amount of time in chunk search. Moreover, the “no chunking” simulation suggests that chunking was advantageous for recall despite the rather low probability of chunk retrieval. This is in line with previous claims that chunking is a general information-processing mechanism. Gobet and colleagues claimed that there is “substantial evidence for a unifying information-processing mechanism, known as ‘chunking’” [41, p. 236]. Moreover, Mathy and Feldman stated that “memory involves a kind of reflexive data compression, whereby material to be encoded is automatically analyzed for structure and redundancy” [12, p. 357]. Chunking, i.e., the search for known structures in processed information, seems to be initiated whenever information is processed. The initiation does not depend on knowledge or expertise. Even if no chunk is recognized in most cases, chunking appears to be sustained.

To provide further proof for the universal nature of chunking, future studies could conduct the present experiment with a sample of non-musicians. This would reveal if chunking is initiated even if participants have absolutely no knowledge on major triads. In addition, it would be interesting to analyze chunking in a multi-media context, in which sound is presented together with note symbols [42].

Advancing TBRS*C

Guida and colleagues [43] provided evidence from neuroimaging experiments that expertise acquisition might progress in two stages. At the first stage, chunks start to become available in LTM which means that they do not have to be built during processing by binding elements in WM. Thus, the focus shifts from chunk creation to chunk retrieval. Physiologically, this is associated with a decrease of the cerebral activation in WM areas. At the second stage, more comprehensive knowledge structures such as templates [4] or retrieval structures [5] are developed that allow using parts of LTM as WM. This is associated with an increased involvement of LTM brain areas in WM tasks.

Currently, TBRS*C only represents the former stage. Simple, non-hierarchical chunks are available in LTM and can be retrieved after encoding new stimuli. To account for the second stage of expertise acquisition and thereby advance TBRS*C as a model of expert memory, knowledge structures could be implemented in the simulations.

Templates have meaningful structures as a fixed core and slots that allow extending this core with variable information [4]. In the case of tonal music, two-note pairs (such as C-E) might denote a fixed core. Complemented with a third note, this two-note core can form different meaningful tonal structures such as a major triad (C-E–G) or an augmented triad (C-E–G#). In TBRS*C, this could be implemented by adding two-note pairs as well as triads to LTM and by programming the simulation to search for chunks after the second note and to extend encoded chunks to form three-note templates. For example, the simulation might first encode C-E as a chunk and then, if the following note is G, might extend this chunk to form a C-E-G major triad template.

Retrieval structures are based on a different logic than templates. They could rather be described as hierarchical structures in which multiple chunks can be encoded within supergroups [5]. In the musical domain, multiple major triads (such as C-E-G and F-G-C) belong to the same scale (such as C major) and hence are more closely associated with each other than with major triads from other scales (such as D-F#-A). This concept of supergroups could again be implemented by adapting the LTM of TBRS*C. If the LTM would not only contain major triads but also groups of multiple major triads, the simulation could encode not only three but even six notes as a single unit. Future studies might implement these two kinds of knowledge structures in TBRS*C and then compare which simulation provides a better fit to human data.

Conclusion

In conclusion, we assumed that during a complex span task, the main cognitive processes would be encoding, i.e., the association of items and positions through Hebbian learning [18], refreshing/decay, i.e., the increase or decrease of the strength of item-position-associations due to short-term neural plasticity [23, 24], and chunking, i.e., the recognition and encoding of known units in novel stimuli, with the knowledge of these units being acquired through long-term Hebbian learning [21]. These biologically plausible cognitive processes were mathematically implemented in the TBRS*C model. This model was then applied to human data from a complex span task with musical notes to reveal details about expertise differences in WM functioning. This provided evidence that experts’ WM is characterized by faster encoding and chunk search, and more reliable recognition of chunks. Both contribute to the better performance of experts’ WM, as the former leads to an increase in refresh times and the latter renders refreshing more effective. TBRS*C has proven a useful tool for the research on expert cognition. We hope that future studies make use of this tool and thereby achieve further insights how expertise can be conceptualized in the Time-Based Resource Sharing model.