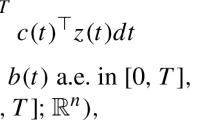Abstract
We study two-stage robust optimization problems with mixed discrete-continuous decisions in both stages. Despite their broad range of applications, these problems pose two fundamental challenges: (i) they constitute infinite-dimensional problems that require a finite-dimensional approximation, and (ii) the presence of discrete recourse decisions typically prohibits duality-based solution schemes. We address the first challenge by studying a K-adaptability formulation that selects K candidate recourse policies before observing the realization of the uncertain parameters and that implements the best of these policies after the realization is known. We address the second challenge through a branch-and-bound scheme that enjoys asymptotic convergence in general and finite convergence under specific conditions. We illustrate the performance of our algorithm in numerical experiments involving benchmark data from several application domains.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Dynamic decision-making under uncertainty, where actions need to be taken both in anticipation of and in response to the realization of a priori uncertain problem parameters, arguably forms one of the most challenging domains of operations research and optimization theory. Despite intensive research efforts over the past six decades, many uncertainty-affected optimization problems resist solution, and even our understanding of the complexity of these problems remains incomplete.
In the last two decades, robust optimization has emerged as a promising methodology to counter some of the intricacies associated with decision-making under uncertainty. The rich theory on static robust optimization problems, in which all decisions have to be taken before the uncertainty is resolved, is summarized in [2, 4, 16]. However, dynamic robust optimization problems, in which some of the decisions can adapt to the observed uncertainties, are still poorly understood.
This paper is concerned with two-stage robust optimization problems of the form
where \({\mathcal {X}} \subseteq \mathbb {R}^{N_1}\), \({\mathcal {Y}} \subseteq \mathbb {R}^{N_2}\) and \(\varXi \subseteq \mathbb {R}^{N_p}\) constitute nonempty and bounded mixed-integer linear programming (MILP) representable sets, \(\varvec{c} \in \mathbb {R}^{N_1}\), and the functions \(\varvec{d} : \varXi \mapsto \mathbb {R}^{N_2}\), \(\varvec{T} : \varXi \mapsto \mathbb {R}^{L \times N_1}\), \(\varvec{W} : \varXi \mapsto \mathbb {R}^{L \times N_2}\) and \(\varvec{h} : \varXi \mapsto \mathbb {R}^L\) are affine. In problem (1), the vector \(\varvec{x}\) represents the first-stage (or ‘here-and-now’) decisions which are taken before the value of the uncertain parameter vector \(\varvec{\xi }\) from within the uncertainty set \(\varXi \) is observed. The vector \(\varvec{y}\), on the other hand, denotes the second-stage (‘wait-and-see’ or ‘adjustable’) decisions that can adapt to the realized value of \(\varvec{\xi }\). Due to the presence of the adjustable decisions \(\varvec{y}\), two-stage robust optimization problems are also referred to as adjustable robust optimization problems [3, 38]. We emphasize that problem (1) can have a random recourse, i.e., the recourse matrix \(\varvec{W}\) may depend on the uncertain parameters \(\varvec{\xi }\). Moreover, we do not assume a relatively complete recourse; that is, for some first-stage decisions \(\varvec{x} \in {\mathcal {X}}\), there can be parameter realizations \(\varvec{\xi } \in \varXi \) such that there is no feasible second-stage decision \(\varvec{y}\). Also, we do not assume that the sets \({\mathcal {X}}\), \({\mathcal {Y}}\) or \(\varXi \) are convex.
Remark 1
(Uncertain First-Stage Objective Coefficients) The assumption that \(\varvec{c}\) is deterministic does not restrict generality. Indeed, problem (1) accounts for uncertain first-stage objective coefficients \(\varvec{c}' : \varXi \mapsto \mathbb {R}^{N_1}\) if we augment the second-stage decisions \(\varvec{y}\) to \((\varvec{y}, \varvec{y}')\), replace the second-stage objective coefficients \(\varvec{d}\) with \((\varvec{d}, \varvec{c}')\) and impose the constraint that \(\varvec{y}' = \varvec{x}\).
Even in the special case where \({\mathcal {X}}\), \({\mathcal {Y}}\) and \(\varXi \) are linear programming (LP) representable, problem (1) has been shown to be NP-hard [23]. Nevertheless, problem (1) simplifies considerably if the sets \({\mathcal {Y}}\) and \(\varXi \) are LP representable. For this setting, several approximate solution schemes have been proposed that replace the second-stage decisions with decision rules, i.e., parametric classes of linear or nonlinear functions of \(\varvec{\xi }\) [3, 15, 17, 18, 28]. If we further assume that \(\varvec{d}\), \(\varvec{T}\) and \(\varvec{W}\) are deterministic and \(\varXi \) is of simple form (e.g., a budget uncertainty set), a number of exact solution schemes based on Benders’ decomposition [10, 26, 34, 40] and semi-infinite programming [1, 39] have been developed.
Problem (1) becomes significantly more challenging if the set \({\mathcal {Y}}\) is not LP representable. For this setting, conservative MILP approximations have been developed in [20, 36] by partitioning the uncertainty set \(\varXi \) into hyperrectangles and restricting the continuous and integer recourse decisions to affine and constant functions of \(\varvec{\xi }\) over each hyperrectangle, respectively. These a priori partitioning schemes have been extended to iterative partitioning approaches in [6, 31]. Iterative solution approaches based on decision rules have been proposed in [7, 8]. However, to the best of our knowledge, none of these approaches has been shown to converge to an optimal solution of problem (1). For the special case where problem (1) has a relatively complete recourse, \(\varvec{d}\), \(\varvec{T}\) and \(\varvec{W}\) are deterministic and the optimal value of the second-stage problem is quasi-convex over \(\varXi \), the solution scheme of [39] has been extended in [41] to a nested semi-infinite approach that can solve instances of problem (1) with MILP representable sets \({\mathcal {Y}}\) and \(\varXi \) to optimality in finite time.
Instead of solving problem (1) directly, we study its K-adaptability problem
where  . Problem (2) determines K non-adjustable second-stage policies \(\varvec{y}_1, \ldots , \varvec{y}_K\) here-and-now and subsequently selects the best of these policies in response to the observed value of \(\varvec{\xi }\). If all policies are infeasible for some realization \(\varvec{\xi } \in \varXi \), then the solution \((\varvec{x}, \varvec{y})\) attains the objective value \(+ \infty \). By construction, the K-adaptability problem (2) bounds the two-stage robust optimization problem (1) from above.
. Problem (2) determines K non-adjustable second-stage policies \(\varvec{y}_1, \ldots , \varvec{y}_K\) here-and-now and subsequently selects the best of these policies in response to the observed value of \(\varvec{\xi }\). If all policies are infeasible for some realization \(\varvec{\xi } \in \varXi \), then the solution \((\varvec{x}, \varvec{y})\) attains the objective value \(+ \infty \). By construction, the K-adaptability problem (2) bounds the two-stage robust optimization problem (1) from above.
Our interest in problem (2) is motivated by two observations. Firstly, problem (2) has been shown to be a remarkably good approximation of problem (1), both in theory and in numerical experiments [5, 24]. Secondly, and perhaps more importantly, the K-adaptability problem conforms well with human decision-making, which tends to address uncertainty by developing a small number of contingency plans, rather than devising the optimal response for every possible future state of the world. For instance, practitioners may prefer a limited number of contingency plans to full flexibility in the second stage for operational (e.g., in production planning or logistics) or organizational (e.g., in emergency response planning) reasons.
The K-adaptability problem was first studied in [5], where the authors reformulate the 2-adaptability problem as a finite-dimensional bilinear program and solve it heuristically. The authors also show that the 2-adaptability problem is NP-hard even if \(\varvec{d}\), \(\varvec{T}\) and \(\varvec{W}\) are deterministic, and they develop necessary conditions for the K-adaptability problem (2) to outperform the static robust problem (where all decisions are taken here-and-now). The relationship between the K-adaptability problem (2) and static robust optimization is further explored in [9] for the special case where \(\varvec{T}\) and \(\varvec{W}\) are deterministic. The authors show that the gaps between both problems and the two-stage robust optimization problem (1) are intimately related to geometric properties of the uncertainty set \(\varXi \). Finite-dimensional MILP reformulations for problem (2) are developed in [24] under the additional assumption that both the here-and-now decisions \(\varvec{x}\) and the wait-and-see decisions \(\varvec{y}\) are binary. The authors show that both the size of the reformulations as well as their gaps to the two-stage robust optimization problem (1) depend on whether the uncertainty only affects the objective coefficients \(\varvec{d}\), or whether the constraint coefficients \(\varvec{T}\), \(\varvec{W}\) and \(\varvec{h}\) are uncertain as well. Finally, it is shown in [12, 13] that for polynomial time solvable deterministic combinatorial optimization problems, the associated instances of problem (2) without first-stage decisions \(\varvec{x}\) can also be solved in polynomial time if all of the following conditions hold: (i) \(\varXi \) is convex, (ii) only the objective coefficients \(\varvec{d}\) are uncertain, and (iii) \(K > N_2\) policies are sought. This result has been extended to discrete uncertainty sets in [14], in which case pseudo-polynomial solution algorithms can be developed.
In this paper, we expand the literature on the K-adaptability problem in two ways. From an analytical viewpoint, we compare the two-stage robust optimization problem (1) with the K-adaptability problem (2) in terms of their continuity, convexity and tractability. We also investigate when the approximation offered by the K-adaptability problem is tight, and under which conditions the two-stage robust optimization and K-adaptability problems reduce to single-stage problems. From an algorithmic viewpoint, we develop a branch-and-bound scheme for the K-adaptability problem that combines ideas from semi-infinite and disjunctive programming. We establish conditions for its asymptotic and finite time convergence; we show how it can be refined and integrated into state-of-the-art MILP solvers; and, we present a heuristic variant that can address large-scale instances. In contrast to existing approaches, our algorithm can handle mixed continuous and discrete decisions in both stages as well as discrete uncertainty, and allows for modeling continuous second-stage decisions via a novel class of highly flexible piecewise affine decision rules. Extensive numerical experiments on benchmark data from various application domains indicate that our algorithm is highly competitive with state-of-the-art solution schemes for problems (1) and (2).
We highlight that our C++ code is freely available for download on GitHub [33].
The remainder of this paper develops as follows. Section 2 analyzes the geometry and tractability of problems (1) and (2), and it proposes a novel class of piecewise affine decision rules that can be modeled as an instance of problem (2) with continuous second-stage decisions. Section 3 develops a branch-and-bound algorithm for the K-adaptability problem and analyzes its convergence. We present numerical results in Sect. 4, and we offer concluding remarks in Sect. 5.
Notation Vectors and matrices are printed in bold lowercase and uppercase letters, respectively, while scalars are printed in regular font. We use \({\mathbf {e}}_k\) to denote the kth unit basis vector and \({\mathbf {e}}\) to denote the vector whose components are all ones, respectively; their dimensions will be clear from the context. The ith row vector of a matrix \(\varvec{A}\) is denoted by \(\varvec{a}_i^\top \). For a logical expression \({\mathcal {E}}\), we define \(\mathbb {I}[{\mathcal {E}}]\) as the indicator function which takes a value of 1 is \({\mathcal {E}}\) is true and 0 otherwise.
2 Problem analysis
In this section, we analyze the geometry and tractability of the two-stage robust optimization problem (1) and its associated K-adaptability problem (2). Specifically, we characterize the continuity, convexity and tractability of both problems, as well as their relationship to the static robust optimization problem where all decisions are taken here-and-now. We also show how the K-adaptability problem with continuous second-stage decisions enables us to approximate the two-stage robust optimization problem (1) through highly flexible piecewise affine decision rules.
Table 1 summarizes our theoretical results. For the sake of brevity, we relegate the formal statements of these results as well as their proofs to the electronic version of the paper at arxiv.org/abs/1706.07097. In the table, the first-stage problem refers to the overall problems (1) and (2), the evaluation problem refers to the maximization over \(\varvec{\xi } \in \varXi \) for a fixed first-stage decision, and the second-stage problem refers to the inner minimization over \(\varvec{y} \in {\mathcal {Y}}\) or \(k \in {\mathcal {K}}\) for a fixed first-stage decision and a fixed realization of the uncertain problem parameters. The table reveals that despite significant differences in their formulations, the problems (1) and (2) behave very similarly. The most significant difference is caused by the replacement of the optimization over the second-stage decisions \(\varvec{y} \in {\mathcal {Y}}\) in problem (1) with the selection of a candidate policy \(k \in {\mathcal {K}}\) in problem (2). This ensures that the second-stage problem in (2) is always continuous, convex and tractable, whereas the first-stage problem in (2) fails to be convex even if \({\mathcal {X}}\) and \({\mathcal {Y}}\) are convex. Moreover, in contrast to problem (1), the evaluation problem in (2) remains continuous as long as either the objective function or the constraints are unaffected by uncertainty. For general problem instances, however, neither of the two evaluation problems is continuous. As we will see in Sect. 3.2, this directly impacts the convergence of our branch-and-bound algorithm, which only takes place asymptotically in general. Note that the convexity of the problems (1) and (2) does not depend on the shape of the uncertainty set \(\varXi \).
2.1 Incorporating decision rules in the K-adaptability problem
Although the K-adaptability problem (2) selects the best candidate policy \(\varvec{y}_k\) in response to the observed parameter realization \(\varvec{\xi } \in \varXi \), the policies \(\varvec{y}_1, \ldots , \varvec{y}_K\)—once selected in the first stage—no longer depend on \(\varvec{\xi }\). This lack of dependence on the uncertain problem parameters can lead to overly conservative approximations of the two-stage robust optimization problem (1) when the second-stage decisions are continuous. In this section, we show how the K-adaptability problem (2) can be used to generalize affine decision rules, which are commonly used to approximate continuous instances of the two-stage robust optimization problem (1). We note that existing schemes, such as [13, 24], cannot be used for this purpose as they require the wait-and-see decisions \(\varvec{y}\) to be binary.
Throughout this section, we assume that problem (1) has purely continuous second-stage decisions (that is, \({\mathcal {Y}}\) is LP representable), a deterministic objective function (that is, \(\varvec{d} (\varvec{\xi }) = \varvec{d}\) for all \(\varvec{\xi } \in \varXi \)) and fixed recourse (that is, \(\varvec{W} (\varvec{\xi }) = \varvec{W}\) for all \(\varvec{\xi } \in \varXi \)). The assumption of continuous second-stage decisions allows us to assume, without loss of generality, that \({\mathcal {Y}} = \mathbb {R}^{N_2}\) as any potential restrictions can be absorbed in the second-stage constraints.
The affine decision rule approximation to the two-stage robust optimization problem (1) is
where \(\varvec{y} : \varXi \overset{1}{\mapsto } \mathbb {R}^{N_2}\) indicates that \(\varvec{y} (\varvec{\xi }) = \varvec{y}^{0} + \varvec{Y} \varvec{\xi }\) for some \(\varvec{y}^{0} \in \mathbb {R}^{N_2}\) and \(\varvec{Y} \in \mathbb {R}^{N_2 \times N_p}\), see [3]. This problem provides a conservative approximation to the two-stage robust optimization problem (1) since we replace the space of all (possibly non-convex and discontinuous) second-stage policies \(\varvec{y} : \varXi \mapsto \mathbb {R}^{N_2}\) with the subspace of all affine second-stage policies \(\varvec{y} : \varXi \overset{1}{\mapsto } \mathbb {R}^{N_2}\). In a similar spirit, we define the subspace of all piecewise affine decision rules \(\varvec{y} : \varXi \overset{K}{\mapsto } \mathbb {R}^{N_2}\) with K pieces as
Note that our earlier definition of \(\varvec{y} : \varXi \overset{1}{\mapsto } \mathbb {R}^{N_2}\) is identical to our definition of \(\varvec{y} : \varXi \overset{K}{\mapsto } \mathbb {R}^{N_2}\) if \(K = 1\). For \(K > 1\), the decision rules \(\varvec{y} : \varXi \overset{K}{\mapsto } \mathbb {R}^{N_2}\) may be non-convex and discontinuous, and the regions where \(\varvec{y}\) is affine may be non-closed and non-convex. We highlight that the points of nonlinearity are determined by the optimization problem. This is in contrast to many existing solution schemes for piecewise affine decision rules, such as [8, 15, 17, 18], where these points are specified ad hoc by the decision-maker.
Observation 1
The piecewise affine decision rule problem with fixed recourse
is equivalent to the K-adaptability problem with random recourse
where \(\hat{{\mathcal {Y}}} = \{(\varvec{y}^0, \varvec{Y}, \varvec{z}) \in \mathbb {R}^{N_2} \times \mathbb {R}^{N_2 \times N_p} \times (\mathbb {R}^{N_p} \times \mathbb {R}^{N_p L}) \,:\, \varvec{z} = (\varvec{z}_{1}, \varvec{z}_{2}) \text { with } \varvec{z}_1 = \varvec{Y}^\top \varvec{d} \text { and } \varvec{z}_2 = [\varvec{w}_1^\top \varvec{Y} \; \ldots \; \varvec{w}_L^\top \varvec{Y} ]^\top \}\), \(\varvec{\hat{d}} (\varvec{\xi }) = \varvec{\xi }\) and \(\varvec{\hat{W}} (\varvec{\xi }) = \text {diag }(\varvec{\xi }^\top , \, \ldots , \, \varvec{\xi }^\top ) \in \mathbb {R}^{L \times N_p L}\).
Proof
Problem (4) is infeasible if and only if for every \(\varvec{x} \in {\mathcal {X}}\) and \((\varvec{y}^0, \varvec{Y}, \varvec{z}) \in \hat{{\mathcal {Y}}}^K\) there is a \(\varvec{\xi } \in \varXi \) such that \(\varvec{T} (\varvec{\xi }) \varvec{x} + \varvec{W} \varvec{y}_k^0 + \varvec{\hat{W}} (\varvec{\xi }) \varvec{z}_{k2} \not \le \varvec{h} (\varvec{\xi })\) for all \(k = 1,\ldots , K\), which in turn is the case if and only if for every \(\varvec{x} \in {\mathcal {X}}\) and \((\varvec{y}^0_k, \varvec{Y}_k) \in \mathbb {R}^{N_2} \times \mathbb {R}^{N_2 \times N_p}\), \(k = 1,\ldots , K\) there is a \(\varvec{\xi } \in \varXi \) such that \(\varvec{T} (\varvec{\xi }) \varvec{x} + \varvec{W} \varvec{y}_k^0 + \varvec{W} \varvec{Y}_k \varvec{\xi } \not \le \varvec{h} (\varvec{\xi })\) for all \(k = 1,\ldots , K\); that is, if and only if problem (3) is infeasible. We thus assume that both (3) and (4) are feasible. In this case, we verify that every feasible solution \((\varvec{x}, \varvec{y}^0, \varvec{Y}, \varvec{z})\) to problem (4) gives rise to a feasible solution \((\varvec{x}, \varvec{y})\), where \(\varvec{y} (\varvec{\xi }) = \varvec{y}_{k(\varvec{\xi })}^0 + \varvec{Y}_{k(\varvec{\xi })} \varvec{\xi }\) and \(k(\varvec{\xi })\) is any element of \(\mathop {\arg \min }\nolimits _{k \in {\mathcal {K}}} \{ \varvec{c}^\top \varvec{x} + \varvec{d}^\top \varvec{y}_k^0 + \varvec{\hat{d}} (\varvec{\xi })^\top \varvec{z}_{k1} \, : \, \varvec{T} (\varvec{\xi }) \varvec{x} + \varvec{W} \varvec{y}_k^0 + \varvec{\hat{W}} (\varvec{\xi }) \varvec{z}_{k2} \le \varvec{h} (\varvec{\xi })\}\), in problem (3) that attains the same worst-case objective value. Similarly, every optimal solution\((\varvec{x}, \varvec{y})\) to problem (3) gives rise to an optimal solution \((\varvec{x}, \varvec{y}^0, \varvec{Y}, \varvec{z})\), where \(\varvec{z}_k = (\varvec{z}_{k1}, \varvec{z}_{k2})\) with \(\varvec{z}_{k1} = \varvec{Y}_k^\top \varvec{d}\) and \(\varvec{z}_{k2} = [\varvec{w}_1^\top \varvec{Y}_k \; \ldots \; \varvec{w}_L^\top \varvec{Y}_k ]^\top \), \(k = 1, \ldots , K\), in problem (4). Hence, (3) and (4) share the same optimal value and the same sets of optimal solutions.\(\square \)
We close with an example that illustrates the benefits of piecewise affine decision rules.
Example 1
Consider the following instance of the two-stage robust optimization problem (1), which has been proposed in [19, Sect. 5.2]:
The optimal second-stage policy is \(\varvec{y}^\star (\varvec{\xi }) = ([\xi _1 + \xi _2]_+, \, [\xi _1 - \xi _2]_+, \, [-\xi _1 + \xi _2]_+, \, [-\xi _1 - \xi _2]_+)\), where \([ \cdot ]_+ = \max \{ \cdot , 0 \}\), and it results in the optimal second-stage value function \(Q^\star (\varvec{\xi }) = [\xi _1 + \xi _2]_+ + [\xi _1 - \xi _2]_+ + [-\xi _1 + \xi _2]_+ + [-\xi _1 - \xi _2]_+\) with a worst-case objective value of 2, see Fig. 1. The best affine decision rule\(\varvec{y}^1 : \varXi \overset{1}{\mapsto } \mathbb {R}^4_+\) is \(\varvec{y}^1 (\varvec{\xi }) = \left( 1 + \xi _2, \, 1 + \xi _1, \, 1 - \xi _1, \, 1 - \xi _2\right) \), and it results in the constant second-stage value function \(Q^1 (\varvec{\xi }) = 4\). The best 2-adaptable affine decision rule\(\varvec{y}^2 : \varXi \overset{2}{\mapsto } \mathbb {R}^4_+\), on the other hand, is given by
and it results in the constant second-stage value function \(Q^2(\varvec{\xi }) = 2\). Thus, 2-adaptable affine decision rules are optimal in this example. Figure 2 illustrates the optimal value, the affine approximation and the 2-adaptable affine approximation of the decision variable \(y_3\).
The optimal second-stage value function in Example 1 is given by the first-order cone \(Q^\star (\varvec{\xi }) = [\xi _1 + \xi _2]_+ + [\xi _1 - \xi _2]_+ + [-\xi _1 + \xi _2]_+ + [-\xi _1 - \xi _2]_+\)
The piecewise affine decision rules presented here can be readily combined with discrete second-stage decisions. For the sake of brevity, we omit the details of this straightforward extension.
3 Solution scheme
Our solution scheme for the K-adaptability problem (2) is based on a reformulation as a semi-infinite disjunctive program which we present next.
Observation 2
The K-adaptability problem (2) is equivalent to
Moreover, if some of the constraints in problem (5) are deterministic, i.e., they do not depend on \(\varvec{\xi }\), then they can be moved outside the disjunction and instead be enforced for all \(k \in {\mathcal {K}}\).
In the following, we stipulate that the optimal value of (5) is \(+ \infty \) whenever it is infeasible.
Proof of Observation 2
Problem (2) is infeasible if and only if (iff) for every \(\varvec{x} \in {\mathcal {X}}\) and \(\varvec{y} \in {\mathcal {Y}}^K\) there is a \(\varvec{\xi } \in \varXi \) such that \(\varvec{T} (\varvec{\xi }) \varvec{x} + \varvec{W} (\varvec{\xi }) \varvec{y}_k \not \le \varvec{h} (\varvec{\xi })\) for all \(k \in {\mathcal {K}}\), which in turn is the case iff for every \(\varvec{x} \in {\mathcal {X}}\) and \(\varvec{y} \in {\mathcal {Y}}^K\), the disjunction in (5) is violated for at least one \(\varvec{\xi } \in \varXi \); that is, iff problem (5) is infeasible. We thus assume that both (2) and (5) are feasible. In this case, one readily verifies that every feasible solution \((\varvec{x}, \varvec{y})\) to problem (2) gives rise to a feasible solution \((\theta , \varvec{x}, \varvec{y})\), where \(\theta = \sup \nolimits _{\varvec{\xi } \in \varXi }\; \inf \limits _{k \in {\mathcal {K}}} \{ \varvec{c}^\top \varvec{x} + \varvec{d} (\varvec{\xi })^\top \varvec{y}_k : \varvec{T} (\varvec{\xi }) \varvec{x} + \varvec{W} (\varvec{\xi }) \varvec{y}_k \le \varvec{h} (\varvec{\xi })\}\), in problem (5) with the same objective value. Likewise, any optimal solution \((\theta , \varvec{x}, \varvec{y})\) to problem (5) corresponds to an optimal solution \((\varvec{x}, \varvec{y})\) in problem (2). Hence, (2) and (5) share the same optimal value and the same sets of optimal solutions.
We now claim that if \(\varvec{t}_l (\varvec{\xi })^\top = \varvec{t}_l^\top \), \(\varvec{w}_l (\varvec{\xi })^\top = \varvec{w}_l^\top \) and \(h_l (\varvec{\xi }) = h_l\) for all \(l \in \{ 1, \ldots , L \} {\setminus } {\mathcal {L}}\), where \({\mathcal {L}} \subseteq \{ 1, \ldots , L \}\), then problem (5) is equivalent to

By construction, every feasible solution \((\theta , \varvec{x}, \varvec{y})\) to problem (5’) is feasible in problem (5). Conversely, fix any feasible solution \((\theta , \varvec{x}, \varvec{y})\) to problem (5) and assume that \(\varvec{t}_l^\top \varvec{x} + \varvec{w}_l^\top \varvec{y}_k > h_l\) for some \(k \in {\mathcal {K}}\) and \(l \in \{ 1, \ldots , L \} {\setminus } {\mathcal {L}}\). In that case, the kth disjunct in (5) is violated for every realization \(\varvec{\xi } \in \varXi \). We can therefore replace \(\varvec{y}_k\) with a different candidate policy \(\varvec{y}_{k'}\) that satisfies \(\varvec{t}_l^\top \varvec{x} + \varvec{w}_l^\top \varvec{y}_{k'} \le h_l\) for all \(l \in \{ 1, \ldots , L \} {\setminus } {\mathcal {L}}\) without sacrificing feasibility. [Note that such a candidate policy \(\varvec{y}_{k'}\) exists since \((\theta , \varvec{x}, \varvec{y})\) is assumed to be feasible in (5)]. Replacing any infeasible policy in this way results in a solution that is feasible in problem (5’).\(\square \)
Problem (5) cannot be solved directly as it contains infinitely many disjunctive constraints. Instead, our solution scheme iteratively solves a sequence of (increasingly tighter) relaxations of this problem that are obtained by enforcing the disjunctive constraints over finite subsets of \(\varXi \). Whenever the solution of such a relaxation violates the disjunction for some realization \(\varvec{\xi } \in \varXi \), we create K subproblems that enforce the disjunction associated with \(\varvec{\xi }\) to be satisfied by the kth disjunct, \(k = 1, \ldots , K\). Our solution scheme is reminiscent of discretization methods employed in semi-infinite programming, which iteratively replace an infinite set of constraints with finite subsets and solve the resulting discretized problems. Indeed, our scheme can be interpreted as a generalization of Kelley’s cutting-plane method [11, 27] applied to semi-infinite disjunctive programs. In the special case where \(K=1\), our method reduces to the cutting-plane method for (static) robust optimization problems proposed in [30].
In the remainder of this section, we describe our basic branch-and-bound scheme (Sect. 3.1), we study its convergence (Sect. 3.2), we discuss algorithmic variants to the basic scheme that can enhance its numerical performance (Sect. 3.3), and we present a heuristic variant that can address problems of larger scale (Sect. 3.4).
3.1 Branch-and-bound algorithm
Our solution scheme iteratively solves a sequence of scenario-based K-adaptability problems and separation problems. We define both problems first, and then we describe the overall algorithm.
The Scenario-BasedK-Adaptability Problem For a collection \(\varXi _1, \ldots , \varXi _K\) of finite subsets of the uncertainty set \(\varXi \), we define the scenario-based K-adaptability problem as
If \({\mathcal {X}}\) and \({\mathcal {Y}}\) are convex, problem (6) is an LP; otherwise, it is an MILP. The problem is closely related to a relaxation of the semi-infinite disjunctive program (5) that enforces the disjunction only over the realizations \(\varvec{\xi } \in \bigcup _{k \in {\mathcal {K}}} \varXi _k\). More precisely, problem (6) can be interpreted as a restriction of that relaxation which requires the kth candidate policy \(\varvec{y}_k\) to be worst-case optimal for all realizations \(\varvec{\xi } \in \varXi _k\), \(k \in {\mathcal {K}}\). We obtain an optimal solution \((\theta , \varvec{x}, \varvec{y}_k)\) to the relaxed semi-infinite disjunctive program by solving \({\mathcal {M}} (\varXi _1, \ldots , \varXi _K)\) for all partitions \((\varXi _1, \ldots , \varXi _K)\) of \(\bigcup _{k \in {\mathcal {K}}} \varXi _k\) and reporting the optimal solution \((\theta , \varvec{x}, \varvec{y}_k)\) of the problem \({\mathcal {M}} (\varXi _1, \ldots , \varXi _K)\) with the smallest objective value.
If \(\varXi _k = \emptyset \) for all \(k \in {\mathcal {K}}\), then problem (6) is unbounded, and we stipulate that its optimal value is \(-\infty \) and that its optimal value is attained by any solution \((-\infty , \varvec{x}, \varvec{y})\) with \((\varvec{x}, \varvec{y}) \in {\mathcal {X}} \times {\mathcal {Y}}^K\). Otherwise, if problem (6) is infeasible for \(\varXi _1,\ldots ,\varXi _K\), then we define its optimal value to be \(+ \infty \). In all other cases, the optimal value of problem (6) is finite and it is attained by an optimal solution \((\theta , \varvec{x}, \varvec{y})\) since \({\mathcal {X}}\) and \({\mathcal {Y}}\) are compact.
Remark 2
(Decomposability) For K-adaptability problems without first-stage decisions \(\varvec{x}\), problem (6) decomposes into K scenario-based static robust optimization problems that are only coupled through the constraints referencing the epigraph variable \(\theta \). In this case, we can recover an optimal solution to problem (6) by solving each of the K static problems individually and identifying the optimal \(\theta \) as the maximum of their optimal values.
The Separation Problem. For a feasible solution \((\theta , \varvec{x}, \varvec{y})\) to the scenario-based K-adaptability problem (6), we define the separation problem as
for \({\mathcal {S}} : \mathbb {R} \cup \{- \infty \}\times {\mathcal {X}} \times {\mathcal {Y}}^K \mapsto \mathbb {R} \cup \{ + \infty \}\) and \(S : \mathbb {R} \cup \{- \infty \}\times {\mathcal {X}} \times {\mathcal {Y}}^K \times \varXi \mapsto \mathbb {R} \cup \{ + \infty \}\). Whenever it is positive, the innermost maximum in the definition of \(S (\theta , \varvec{x}, \varvec{y}, \varvec{\xi })\) records the maximum constraint violation of the candidate policy \(\varvec{y}_k\) under the parameter realization \(\varvec{\xi } \in \varXi \). Likewise, the quantity \(\varvec{c}^\top \varvec{x} + \varvec{d} (\varvec{\xi })^\top \varvec{y}_k - \theta \) denotes the excess of the objective value of \(\varvec{y}_k\) under the realization \(\varvec{\xi }\) over the current candidate value of the worst-case objective, \(\theta \). Thus, \(S (\theta , \varvec{x}, \varvec{y}, \varvec{\xi })\) is strictly positive if and only if every candidate policy \(\varvec{y}_k\) either is infeasible or results in an objective value greater than \(\theta \) under the realization \(\varvec{\xi } \in \varXi \). Whenever \(\theta \) is finite, the separation problem is feasible and bounded, and it has an optimal solution since \(\varXi \) is nonempty and compact. Otherwise, we have \({\mathcal {S}}(\theta , \varvec{x}, \varvec{y}) = + \infty \), and the optimal value is attained by any \(\varvec{\xi } \in \varXi \).
Observation 3
The separation problem (7) is equivalent to the MILP
This problem can be solved in polynomial time if \(\varXi \) is convex and the number of policies K is fixed.
Proof
Fix any feasible solution \((\theta , \varvec{x}, \varvec{y})\) to the scenario-based K-adaptability problem (6). For every \(\varvec{\xi } \in \varXi \), we can construct a feasible solution \((\zeta , \varvec{\xi }, \varvec{z})\) to problem (8) with \(\zeta = S (\theta , \varvec{x}, \varvec{y}, \varvec{\xi })\) by setting \(z_{k0} = 1\) if \(\varvec{c}^\top \varvec{x} + \varvec{d} (\varvec{\xi })^\top \varvec{y}_k - \theta \ge \varvec{t}_l (\varvec{\xi })^\top \varvec{x} + \varvec{w}_l (\varvec{\xi })^\top \varvec{y}_k - h_l (\varvec{\xi })\) for all \(l = 1, \ldots , L\) and \(z_{kl} = 1\) for \(l \in \mathop {\arg \max }\nolimits _{l \in \{1, \ldots , L\}} \left\{ \varvec{t}_l (\varvec{\xi })^\top \varvec{x} + \varvec{w}_l (\varvec{\xi })^\top \varvec{y}_k - h_l (\varvec{\xi }) \right\} \) otherwise (where ties can be broken arbitrarily). We thus conclude that \({\mathcal {S}} (\theta , \varvec{x}, \varvec{y})\) is less than or equal to the optimal value of problem (8). Likewise, every feasible solution \((\zeta , \varvec{\xi }, \varvec{z})\) to problem (8) satisfies \(\zeta \le \max \big \{ \varvec{c}^\top \varvec{x} + \varvec{d} (\varvec{\xi })^\top \varvec{y}_k - \theta , \; \max \nolimits _{l \in \{ 1, \ldots , L \}} \; \{ \varvec{t}_l (\varvec{\xi })^\top \varvec{x} + \varvec{w}_l (\varvec{\xi })^\top \varvec{y}_k - h_l (\varvec{\xi }) \} \big \}\) for all \(k \in {\mathcal {K}}\); that is, \(\zeta \le S (\theta , \varvec{x}, \varvec{y}, \varvec{\xi })\). Thus, the optimal value of problem (8) is less than or equal to \({\mathcal {S}} (\theta , \varvec{x}, \varvec{y})\) as well.
If the number of policies K is fixed and the uncertainty set \(\varXi \) is convex, then problem (8) can be solved by enumerating all \((L + 1)^K\) possible choices for \(\varvec{z}\), solving the resulting linear programs in \(\zeta \) and \(\varvec{\xi }\) and reporting the solution with the maximum value of \(\zeta \).\(\square \)
The Algorithm Our solution scheme solves a sequence of scenario-based K-adaptability problems (6) over monotonically increasing scenario sets \(\varXi _k\), \(k \in {\mathcal {K}}\). At each iteration, the separation problem (8) identifies a new scenario \(\varvec{\xi } \in \varXi \) to be added to these sets.
- 1.
Initialize Set \({\mathcal {N}} \leftarrow \{ \tau ^0 \}\) (node set), where \(\tau ^0 = (\varXi _1^0, \ldots , \varXi _K^0)\) with \(\varXi _k^0 = \emptyset \) for all \(k \in {\mathcal {K}}\) (root node). Set \((\theta ^\text {i}, \varvec{x}^\text {i}, \varvec{y}^\text {i}) \leftarrow (+\infty , \emptyset , \emptyset )\) (incumbent solution).
- 2.
Check convergence If \({\mathcal {N}} = \emptyset \), then stop and declare infeasibility (if \(\theta ^\text {i} = +\infty \)) or report \((\varvec{x}^\text {i}, \varvec{y}^\text {i})\) as an optimal solution to problem (2).
- 3.
Select node Select a node \(\tau = (\varXi _1, \ldots , \varXi _K)\) from \({\mathcal {N}}\). Set \({\mathcal {N}} \leftarrow {\mathcal {N}} {\setminus } \{ \tau \}\).
- 4.
Process node Let \((\theta , \varvec{x}, \varvec{y})\) be an optimal solution to the scenario-based K-adaptability problem (6) If \(\theta \ge \theta ^\text {i}\), then go to Step 2.
- 5.
Check feasibility Let \((\zeta , \varvec{\xi }, \varvec{z})\) be an optimal solution to the separation problem (8). If \(\zeta \le 0\), then set \((\theta ^\text {i}, \varvec{x}^\text {i}, \varvec{y}^\text {i}) \leftarrow (\theta , \varvec{x}, \varvec{y})\) and go to Step 2; otherwise, if \(\zeta > 0\), go to Step 6.
- 6.
Branch Instantiate K new nodes \(\tau _1, \ldots , \tau _K\) as follows: \(\tau _k = (\varXi _1, \ldots , \varXi _k \cup \{ \varvec{\xi } \}, \ldots , \varXi _K)\) for each \(k \in {\mathcal {K}}\). Set \({\mathcal {N}} \leftarrow {\mathcal {N}} \cup \{\tau _1, \ldots , \tau _K\}\) and go to Step 3.
Our branch-and-bound algorithm can be interpreted as an uncertainty set partitioning scheme. For a solution \((\theta , \varvec{x}, \varvec{y})\) in Step 4, the sets
describe the regions of the uncertainty set \(\varXi \) for which at least one of the candidate policies is feasible and results in an objective value smaller than or equal to \(\theta \). Step 5 of the algorithm attempts to identify a realization \(\varvec{\xi } \in \varXi {\setminus } \bigcup _{k \in {\mathcal {K}}} \varXi (\theta , \varvec{x}, \varvec{y}_k)\) for which every candidate policy either is infeasible or results in an objective value that exceeds \(\theta \). If there is no such realization, then the solution \((\varvec{x}, \varvec{y})\) is feasible in the K-adaptability problem (2). Otherwise, Step 6 assigns the realization \(\varvec{\xi }\) to each scenario subset \(\varXi _k\), \(k \in {\mathcal {K}}\), in turn. Figure 3 illustrates our solution scheme.
An illustrative example with \(K = 2\) policies. Each cube represents the uncertainty set \(\varXi \) while the shaded regions represent \(\varXi (\theta , \varvec{x}, \varvec{y}_1)\) and \(\varXi (\theta , \varvec{x}, \varvec{y}_2)\). The green and blue dots represent elements of the sets \(\varXi _1\) and \(\varXi _2\), respectively, while the red squares represent the candidate realizations \(\varvec{\xi }\) identified in Step 5 of the algorithm (color figure online)
3.2 Convergence analysis
We now establish the correctness of our branch-and-bound scheme, as well as conditions for its asymptotic and finite convergence.
Theorem 1
(Correctness) If the branch-and-bound scheme terminates, then it either returns an optimal solution to problem (2) or correctly identifies the latter as infeasible.
Proof
We first show that if the branch-and-bound scheme terminates on an infeasible problem instance, then the final incumbent solution is \((\theta ^\text {i}, \varvec{x}^\text {i}, \varvec{y}^\text {i}) = (+\infty , \emptyset , \emptyset )\). Indeed, the algorithm can only update the incumbent in Step 5 if the objective value of the separation problem is non-positive. By construction, this is only possible if the algorithm has determined a feasible solution.
We now show that if the branch-and-bound scheme terminates on a feasible problem instance, then the algorithm returns an optimal solution \((\varvec{x}^\text {i}, \varvec{y}^\text {i})\) of problem (2). To this end, assume that \((\varvec{x}^\star , \varvec{y}^\star )\) is an optimal solution of problem (2) with objective value \(\theta ^\star \). Let \({\mathcal {T}}\) be the set of all nodes of the branch-and-bound tree for which \((\theta ^\star , \varvec{x}^\star , \varvec{y}^\star )\) is feasible in the corresponding scenario-based K-adaptability problem (6). Note that \({\mathcal {T}} \ne \emptyset \) since \((\theta ^\star , \varvec{x}^\star , \varvec{y}^\star )\) is feasible in the root node. Let \({\mathcal {T}}' \subseteq {\mathcal {T}}\) be the set of those nodes which have children in \({\mathcal {T}}\), that is, nodes that have been branched in Step 6 of our algorithm. Consider the set \({\mathcal {T}}'' = {\mathcal {T}} {\setminus } {\mathcal {T}}'\). Since the branch-and-bound scheme has terminated, we must have \({\mathcal {T}}'' \ne \emptyset \). Consider an arbitrary node \(\tau \in {\mathcal {T}}''\). Since \(\tau \) has been selected in Step 3 but not been branched in Step 6, either (i) \(\tau \) has been fathomed in Step 4 or if (ii) \(\tau \) has been fathomed in Step 5. In the former case, the solution \((\theta ^\star , \varvec{x}^\star , \varvec{y}^\star )\) must have been weakly dominated by the incumbent solution \((\theta ^\text {i}, \varvec{x}^\text {i}, \varvec{y}^\text {i})\), which therefore must be optimal as well. In the latter case, the incumbent solution must have been updated to \((\theta ^\star , \varvec{x}^\star , \varvec{y}^\star )\).\(\square \)
We now show that our branch-and-bound scheme converges asymptotically to an optimal solution of the K-adaptability problem (2). Our result has two implications: (i) for infeasible problem instances, the algorithm always terminates after finitely many iterations, i.e., infeasibility is detected in finite time; (ii) for feasible problem instances, the algorithm eventually only inspects solutions in the neighborhood of optimal solutions.
Theorem 2
(Asymptotic Convergence) Every accumulation point \(({\hat{\theta }}, \varvec{\hat{x}}, \varvec{\hat{y}})\) of the solutions to the scenario-based K-adaptability problem (6) in an infinite branch of the branch-and-bound tree gives rise to an optimal solution \((\varvec{\hat{x}}, \varvec{\hat{y}})\) of the K-adaptability problem (2) with objective value \({\hat{\theta }}\).
Proof
We denote by \((\theta ^\ell , \varvec{x}^\ell , \varvec{y}^\ell )\) and \((\zeta ^\ell , \varvec{\xi }^\ell , \varvec{z}^\ell )\) the sequences of optimal solutions to the scenario-based K-adaptability problem in Step 4 and the separation problem in Step 5 of the algorithm, respectively, that correspond to the node sequence \(\tau ^\ell \), \(\ell = 0, 1, \ldots \), of some infinite branch of the branch-and-bound tree. Since \({\mathcal {X}}\), \({\mathcal {Y}}\) and \(\varXi \) are compact, the Bolzano–Weierstrass theorem implies that \((\theta ^\ell , \varvec{x}^\ell , \varvec{y}^\ell )\) and \((\zeta ^\ell , \varvec{\xi }^\ell , \varvec{z}^\ell )\) each have at least one accumulation point.
We first show that every accumulation point \(({\hat{\theta }}, \varvec{\hat{x}}, \varvec{\hat{y}})\) of the sequence \((\theta ^\ell , \varvec{x}^\ell , \varvec{y}^\ell )\) corresponds to a feasible solution \((\varvec{\hat{x}}, \varvec{\hat{y}})\) of the K-adaptability problem (2) with objective value \({\hat{\theta }}\). By possibly going over to subsequences, we can without loss of generality assume that the two sequences \((\theta ^\ell , \varvec{x}^\ell , \varvec{y}^\ell )\) and \((\zeta ^\ell , \varvec{\xi }^\ell , \varvec{z}^\ell )\) converge themselves to \(({\hat{\theta }}, \varvec{\hat{x}}, \varvec{\hat{y}})\) and \(({\hat{\zeta }}, \varvec{{\hat{\xi }}}, \varvec{\hat{z}})\), respectively. Assume now that \((\varvec{\hat{x}}, \varvec{\hat{y}})\) does not correspond to a feasible solution of the K-adaptability problem (2) with objective value \({\hat{\theta }}\). Then there is \(\varvec{\xi }^\star \in \varXi \) such that
\(S ({\hat{\theta }}, \varvec{\hat{x}}, \varvec{\hat{y}}, \varvec{\xi }^\star ) \ge \delta \) for some \(\delta > 0\). By construction of the separation problem (8), this implies that
for all \(\ell \) sufficiently large. By taking limits and exploiting the continuity of S, we conclude that
Note, however, that \(S (\theta ^{\ell +1}, \varvec{x}^{\ell +1}, \varvec{y}^{\ell +1}, \varvec{\xi }^\ell ) \le 0\) since \(\varvec{\xi }^\ell \in \varXi ^{\ell + 1}_k\) for some \(k \in {\mathcal {K}}\). Since the sequence \((\theta ^{\ell + 1}, \varvec{x}^{\ell + 1}, \varvec{y}^{\ell + 1})\) also converges to \(({\hat{\theta }}, \varvec{\hat{x}}, \varvec{\hat{y}})\) and \(\varvec{\xi }^\ell \) converges to \(\varvec{{\hat{\xi }}}\), we thus conclude that \(S ({\hat{\theta }}, \varvec{\hat{x}}, \varvec{\hat{y}}, \varvec{{\hat{\xi }}}) \le 0\), which yields the desired contradiction.
We now show that every accumulation point \(({\hat{\theta }}, \varvec{\hat{x}}, \varvec{\hat{y}})\) of the sequence \((\theta ^\ell , \varvec{x}^\ell , \varvec{y}^\ell )\) corresponds to an optimal solution \((\varvec{\hat{x}}, \varvec{\hat{y}})\) of the K-adaptability problem (2) with objective value \({\hat{\theta }}\). Assume to the contrary that \(({\hat{\theta }}, \varvec{\hat{x}}, \varvec{\hat{y}})\) is feasible but suboptimal, that is, there is a feasible solution \((\varvec{x}', \varvec{y}')\) to the K-adaptability problem (2) with objective value \(\theta ' < {\hat{\theta }}\). Let \({\mathcal {T}}\) be the set of all nodes of the branch-and-bound tree for which \((\theta ', \varvec{x}', \varvec{y}')\) is feasible in the corresponding scenario-based K-adaptability problem (6). Note that \({\mathcal {T}} \ne \emptyset \) since \((\theta ', \varvec{x}', \varvec{y}')\) is feasible in the root node. In the following, we distinguish the two cases (i) \(| {\mathcal {T}} | < \infty \) and (ii) \(| {\mathcal {T}} | = \infty \).
If \(| {\mathcal {T}} | < \infty \), then \({\mathcal {T}}\) must contain nodes that were fathomed in Steps 4 or 5 of the algorithm. In that case, however, the incumbent solution must have been updated to \(({\tilde{\theta }}, \tilde{\varvec{x}}, \tilde{\varvec{y}})\) with \({\tilde{\theta }} \le \theta '\) after finitely many iterations. Since the objective values \(\theta ^\ell \) of the scenario-based K-adaptability problems will be arbitrarily close to \({\hat{\theta }}\) for \(\ell \) sufficiently large, the corresponding nodes \(\tau ^\ell \) will also be fathomed in Step 4. This contradicts the assumption that the node sequence \(\tau ^\ell \) corresponds to an infinite branch of the branch-and-bound tree.
If \(| {\mathcal {T}} | = \infty \), on the other hand, the compactness of \({\mathcal {X}}\), \({\mathcal {Y}}\) and \(\varXi \) implies that \((\theta ', \varvec{x}', \varvec{y}')\) constitutes the accumulation point of another infinite sequence \((\theta '^{,\ell }, \varvec{x}'^{,\ell }, \varvec{y}'^{,\ell })\). In that case, too, the objective values \(\theta ^\ell \) and \(\theta '^{,\ell }\) of the scenario-based K-adaptability problems will be arbitrarily close to \({\hat{\theta }}\) and \(\theta '\), respectively, for \(\ell \) sufficiently large. Since \(\theta ' < {\hat{\theta }}\), the algorithm will fathom the tree nodes corresponding to the sequence \((\theta ^\ell , \varvec{x}^\ell , \varvec{y}^\ell )\) in Step 4. This again contradicts the assumption that the node sequence \(\tau ^\ell \) corresponds to an infinite branch of the branch-and-bound tree.
Since both cases \(| {\mathcal {T}} | < \infty \) and \(| {\mathcal {T}} | = \infty \) lead to contradictions, we conclude that the assumed suboptimality of \(({\hat{\theta }}, \varvec{\hat{x}}, \varvec{\hat{y}})\) is wrong. The statement of the theorem thus follows.\(\square \)
Theorem 2 guarantees that after sufficiently many iterations of the algorithm, our scheme generates feasible solutions that are close to an optimal solution of the K-adaptability problem (2). In general, our algorithm may not converge after finitely many iterations. In the following, we discuss a class of problem instances for which finite convergence is guaranteed.
Theorem 3
(Finite Convergence) The branch-and-bound scheme terminates after finitely many iterations, if \({\mathcal {Y}}\) has finite cardinality and only the objective function in problem (2) is uncertain.
Proof
If only the objective function in the K-adaptability problem (2) is uncertain, then the corresponding semi-infinite disjunctive program (5) can be written as
see Observation 2. Thus, the scenario-based K-adaptability problem (6) becomes
and the separation problem (7) can be written as
We now show that if \({\mathcal {Y}}\) has finite cardinality, then our branch-and-bound algorithm terminates after finitely many iterations. To this end, assume that this is not the case, and let \(\tau ^\ell \), \(\ell = 0, 1, \ldots \) be some rooted branch of the tree with infinite length. We denote by \((\theta ^\ell , \varvec{x}^\ell , \varvec{y}^\ell )\) and \((\zeta ^\ell , \varvec{\xi }^\ell , \varvec{z}^\ell )\) the corresponding sequences of optimal solutions to the master and the separation problem, respectively. Since \({\mathcal {Y}}\) has finite cardinality, we must have \(\varvec{y}^{\ell _1} = \varvec{y}^{\ell _2}\) for some \(\ell _1 < \ell _2\).
The solution \((\theta ^{\ell _2}, \varvec{x}^{\ell _2}, \varvec{y}^{\ell _2})\) satisfies \({\mathcal {S}} (\theta ^{\ell _2}, \varvec{x}^{\ell _2}, \varvec{y}^{\ell _2}) > 0\) since \(\tau ^\ell \), \(\ell = 0, 1, \ldots \), is a branch of infinite length. Since \(\varvec{y}^{\ell _2} = \varvec{y}^{\ell _1}\), we thus conclude that
Since \(\varvec{\xi }^{\ell _1}\) is optimal in \({\mathcal {S}} (\theta ^{\ell _1}, \varvec{x}^{\ell _1}, \varvec{y}^{\ell _1})\) and \(S (\theta ^{\ell _1}, \varvec{x}^{\ell _1}, \varvec{y}^{\ell _1}, \varvec{\xi }^{\ell _1}) > 0\), we have
However, since the node \(\tau ^{\ell _2} = (\varXi _1^{\ell _2}, \ldots , \varXi _K^{\ell _2})\) is a descendant of the node \(\tau ^{\ell _1} = (\varXi _1^{\ell _1}, \ldots , \varXi _K^{\ell _1})\), we must have \(\varvec{\xi }^{\ell _1} \in \varXi ^{\ell _2}_k\) for some \(k \in {\mathcal {K}}\). This, along with the fact that \((\theta ^{\ell _2}, \varvec{x}^{\ell _2}, \varvec{y}^{\ell _2})\) is a feasible solution to the master problem \({\mathcal {M}} (\varXi _1^{\ell _2}, \ldots , \varXi _K^{\ell _2})\) and that \(\varvec{y}^{\ell _2} = \varvec{y}^{\ell _1}\), implies that
This yields the desired contradiction and proves the theorem.\(\square \)
We note that the assumption of deterministic constraints is critical in the previous statement.
Example 2
Consider the following instance of the K-adaptability problem (2):
On this instance, our branch-and-bound algorithm generates a tree in which all branches have finite length, except (up to permutations) the sequence of nodes \(\tau ^\ell = (\varXi _1^\ell , \varXi _2^\ell )\), where \((\varXi _1^0, \varXi _2^0) = (\emptyset , \emptyset )\) and \((\varXi _1^\ell , \varXi _2^\ell ) = \left( \big \{ \xi ^0 2^{-i}: i = 0, 1, \ldots , \ell -1 \big \}, \{0\} \right) \), \(\ell > 0\), for some \(\xi ^0 \in (0, 1]\). For the node \(\tau ^\ell \), \(\ell > 1\), the optimal solution of the scenario-based K-adaptability problem (6) is \((\theta ^\ell , y_1^\ell , y_2^\ell ) = (1 - \xi ^0 2^{-\ell +1}, 1, 0)\), while the optimal solution of the separation problem is \((\zeta ^\ell , \xi ^\ell ) = (\xi ^0 2^{-\ell }, \xi ^0 2^{-\ell })\). Thus, our branch-and-bound algorithm does not terminate after finitely many iterations.
We note that every practical implementation of our branch-and-bound scheme will fathom nodes in Step 5 whenever the objective value of the separation problem (7) is sufficiently close to zero (within some \(\epsilon \)-tolerance). This ensures that the algorithm terminates in finite time in practice. Indeed, in Example 2 the objective value of the separation problem is less than \(\epsilon \) for all nodes \(\tau ^\ell \) with \(\ell \ge \log _2 (\xi ^0 \epsilon ^{-1})\), and our branch-and-bound algorithm will fathom the corresponding path of the tree after \({\mathcal {O}} (\log \epsilon ^{-1})\) iterations if we seek \(\epsilon \)-precision solutions.
3.3 Improvements to the basic algorithm
The algorithm of Sect. 3.1 serves as a blueprint that can be extended in multiple ways. In the following, we discuss three enhancements that improve the numerical performance of our algorithm.
Breaking symmetry For any feasible solution \((\varvec{x}, \varvec{y})\) of the K-adaptability problem (2), every solution \((\varvec{x}, \varvec{y}')\), where \(\varvec{y}'\) is one of the K! permutations of the second-stage policies \((\varvec{y}_1, \ldots , \varvec{y}_K)\), is also feasible in (2) and attains the same objective value. This implies that our branch-and-bound tree is highly isomorphic since the scenario-based problems (6) and (8) are identical (up to a permutation of the policies) across many nodes. We can reduce this undesirable symmetry by modifying Step 6 of our branch-and-bound scheme as follows:
6\('\). Branch Let \(K' = 1\) if \(\varXi _1 = \ldots = \varXi _K = \emptyset \) and let \(K' = \min \Big \{K, \, 1 + \max \limits _{k \in {\mathcal {K}}} \big \{k : \varXi _k \ne \emptyset \big \} \Big \}\) otherwise. Instantiate \(K'\) new nodes \(\tau _k = (\varXi _1, \ldots , \varXi _k \cup \{ \varvec{\xi } \}, \ldots , \varXi _K)\), \(k = 1, \ldots , K'\). Set \({\mathcal {N}} \leftarrow {\mathcal {N}} \cup \{\tau _1, \ldots , \tau _{K'}\}\) and go to Step 3.
The modification above is effective only when there are empty scenario sets, i.e., \(\cup _{k \in {\mathcal {K}}'}\varXi _k = \emptyset \) for some \({\mathcal {K}}' \subseteq {\mathcal {K}}\). Nevertheless, it can be shown that empty scenario sets can arise at any tree depth, and the modification causes a significant reduction in the number of generated nodes. Despite generating only a subset of the nodes that our original algorithm constructs, however, the modification above always maintains at least one of the K! solutions symmetric to every feasible solution.
Integration into MILP Solvers. Step 4 of our algorithm solves the scenario-based problem (6) from scratch in every node, despite the fact that two successive problems along any branch of the branch-and-bound tree differ only by the addition of a few constraints. We can leverage this commonality if we integrate our branch-and-bound algorithm into the solution scheme of the MILP solver used for problem (6). In doing so, we can also exploit the advanced facilities commonly present in the state-of-the-art solvers such as warm-starts and cutting planes, among others.
In order to integrate our branch-and-bound algorithm into the solution scheme of the MILP solver, we initialize the solver with the scenario-based problem (6) corresponding to the root node \(\tau ^0\) of our algorithm, see Step 1. The solver then proceeds to solve this problem using its own branch-and-bound procedure. Whenever the solver encounters an integral solution\((\theta , \varvec{x}, \varvec{y}) \in \mathbb {R} \times {\mathcal {X}} \times {\mathcal {Y}}^K\), we solve the associated separation problem (8). If \({\mathcal {S}}(\theta , \varvec{x}, \varvec{y}) > 0\), then we execute Step 6 of our algorithm through a branch callback: we report the K new branches to the solver, which will discard the current solution. Otherwise, if \({\mathcal {S}}(\theta , \varvec{x}, \varvec{y}) \le 0\), then we do not create any new branches, and the solver will accept \((\theta , \varvec{x}, \varvec{y})\) as the new incumbent solution. This ensures that only those solutions which are feasible in problem (5) are accepted as incumbent solutions, and furthermore, that all nodes of our branch-and-bound scheme (not just the root node) are fully explored within the same search tree generated by the MILP solver for solving problem (6) corresponding to the root node \(\tau ^0\) of our algorithm.
Whenever the solver encounters a fractional solution, it will by default branch on an integer variable that is fractional in the current solution. However, if the fractional solution also happens to satisfy \({\mathcal {S}} (\theta , \varvec{x}, \varvec{y}) > 0\), then it is possible to override this default strategy and instead execute Step 6 of our algorithm. In such cases, a heuristic rule can be used to decide whether to branch on integer variables or to branch as in Step 6. In our computational experience, a simple rule that alternates between the default branching rule of the solver and the one defined by Step 6 appears to perform well in practice.
3.4 Modification as a heuristic algorithm
Whenever the number of policies K is large, the solution of the scenario-based K-adaptability problem (6) can be time consuming. In such cases, only a limited number of nodes will be explored by the algorithm in a given amount of computation time, and the quality of the final incumbent solution may be poor. As a remedy, we can reduce the size and complexity of the scenario-based K-adaptability problem (6) by fixing some of its second-stage policies and limiting the total computation time. In doing so, we obtain a heuristic variant of our algorithm that can scale to large values of K.
In our computational experience, a simple heuristic that sequentially solves the 1-, 2-, ..., K-adaptability problems by fixing in each K-adaptability problem all but one of the second-stage policies, \(\varvec{y}_1, \ldots , \varvec{y}_{K-1}\), to their corresponding values in the \((K-1)\)-adaptability problem, performs well in practice. This heuristic is motivated by two observations. First, the resulting scenario-based K-adaptability problems (6) have the same size and complexity as the corresponding scenario-based 1-adaptability problems. Second, in our experiments on instances with uncertain objective coefficients \(\varvec{d}\), we often found that some optimal second-stage policies of the \((K-1)\)-adaptability problem also appear in the optimal solution of the K-adaptability problem. In fact, it can be shown that this heuristic can obtain K-adaptable solutions that improve upon 1-adaptable solutions only if the objective coefficients \(\varvec{d}\) are affected by uncertainty.
4 Numerical results
We now analyze the computational performance of our branch-and-bound scheme in a variety of problem instances from the literature. We consider a shortest path problem with uncertain arc weights (Sect. 4.1), a capital budgeting problem with uncertain cash flows (Sect. 4.2), a variant of the capital budgeting problem with the additional option to take loans (Sect. 4.3), a project management problem with uncertain task durations (Sect. 4.4), and a vehicle routing problem with uncertain travel times (Sect. 4.5). Of these, the first two problems involve only binary decisions, and they can therefore also be solved with the approach described in [24]. In these cases, we show that our solution scheme is highly competitive, and it frequently outperforms the approach of [24]. In contrast, the third and fourth problems also involve continuous decisions, and there is no existing solution approach for their associated K-adaptability problems. However, the project management problem from Sect. 4.4 involves only continuous second-stage decisions, and therefore the corresponding two-stage robust optimization problem (1) can also be approximated using affine decision rules [3], which represent the most popular approach for such problems. In this case, we elucidate the benefits of K-adaptable constant and affine decisions over standard affine decision rules. Finally, the first and last problems involve only binary second-stage decisions and deterministic constraints, and they can therefore also be addressed with the heuristic approach described in [13]. In these cases, we show that the heuristic variant of our algorithm often outperforms the latter approach in terms of solution quality.
For each problem category, we investigate the tradeoffs between computational effort and improvement in objective value of the K-adaptability problem for increasing values of K. We demonstrate that (i) the K-adaptability problem can provide significant improvements over static robust optimization (which corresponds to the case \(K=1\)), and that (ii) our solution scheme can quickly determine feasible solutions of high quality.
We implemented our branch-and-bound algorithm in C++ using the C callable library of CPLEX 12.6 [25]. We note that CPLEX does not directly support the creation of more than two child nodes during branching. However, as the branching Step 6\('\) may create up to K child nodes, we use a binary representation of the underlying K-ary tree (see, e.g., [32]), and implement the branching step using a combination of incumbent and branch callbacks. By using callback functions in this manner, we can integrate our algorithm within CPLEX in a modular fashion while still leveraging advanced MILP technology such as cutting planes, backtracking rules and other heuristics. We caution, however, that the creation of up to K child nodes can result in very large search trees, and potentially cause memory issues. Therefore, to limit the size of our search trees, we use a CPLEX-imposed memory limit of 16GB RAM. We used a constraint feasibility tolerance of \(\epsilon = 10^{-4}\) to accept any incumbent solutions, whereas all other solver options were kept at their default values. Unless mentioned otherwise, we employ a time limit of 7200 s for our branch-and-bound scheme and a time limit of 60 s for the heuristic variant of our algorithm. All experiments were conducted on a single core of an Intel Xeon 2.8 GHz computer.
4.1 Shortest paths
We consider the shortest path problem from [24]. Let \(G = (V, A)\) be a directed graph with nodes \(V = \{1, \ldots , N\}\), arcs \(A \subseteq V \times V\) and arc weights \(d_{ij}(\varvec{\xi }) = (1 + \xi _{ij}/2) d_{ij}^0\), \((i, j) \in A\). Here, \(d_{ij}^0 \in \mathbb {R}_{+}\) represents the nominal weight of the arc \((i, j) \in A\) and \(\xi _{ij}\) denotes the uncertain deviation from the nominal weight. The realizations of the uncertain vector \(\varvec{\xi }\) are known to belong to the set
which stipulates that at most \(\varGamma \) arc weights may maximally deviate from their nominal values.
Let \(s \in V\) and \(t \in V\), \(s \ne t\), denote the source and terminal nodes of G, respectively. The decision-maker aims to choose K paths from s to t here-and-now, i.e., before observing the actual arc weights, such that the worst-case weight of the shortest among the chosen paths is minimized. This problem can be formulated as an instance of the K-adaptability problem (2):
Here, \({\mathcal {Y}}\) denotes the set of all \(s-t\) paths in G; that is,
Note that this problem only contains second-stage decisions and as such, the corresponding two-stage robust optimization problem (1) may be of limited interest in practice. Nevertheless, the K-adaptability problem (2) has important applications in logistics and disaster relief [24].
For each graph size \(N \in \{20, 25, \ldots , 50\}\), we randomly generate 100 problem instances as follows. We assign the coordinates \((u_i, v_i) \in \mathbb {R}^2\) to each node \(i \in V\) uniformly at random from the square \([0, 10]^2\). The nominal weight of the arc \((i,j) \in A\) is defined to be the Euclidean distance between the nodes i and j; that is, \(d_{ij}^0 = \sqrt{(u_i - u_j)^2 + (v_i - v_j)^2}\). The source node s and the terminal node t are defined to be the nodes with the maximum Euclidean distance between them. The arc set A is obtained by removing from the set of all pairwise links the \(\lfloor 0.7 (N^2 - N) \rfloor \) connections with the largest nominal weights. We set the uncertainty budget to \(\varGamma = 3\). Further details on the parameter settings can be found in [24].
Table 2 summarizes the numerical performance of our branch-and-bound scheme for \(K \in \{2, 3, 4\}\). Table 2 indicates that our scheme is able to reliably compute optimal solutions for small values of N and K, while the average optimality gap for large values of N and K is less than 9%. The numerical performance is strongly affected by the value of K; very few of the 4-adaptable instances are solved to optimality within the time limit. This decrease in tractability is partly explained in Fig. 4, which shows the improvement in objective value of the K-adaptability problem over the static problem (where \(K=1\)). Figure 4a shows that the computed 4-adaptable solutions are typically of high quality since they improve upon the static solutions by as much as 13% for large values of N. Moreover, Fig. 4b shows that these solutions are obtained within 1 minute (on average), even for the largest instances. This indicates that the gaps in Table 2 are likely to be very conservative since the majority of computation time is spent on obtaining a certificate of optimality for these solutions. Finally, although not shown in Table 2, instances with \(K=1\) are solved in less than 10 s, on average. This motivates the heuristic variant of our algorithm, which we present next.
Results for the shortest path problem using the exact algorithm. The graphs show the average improvement \(|(\theta _1 - \theta _K)/\theta _1 |\times 100\%\) of the objective value of the K-adaptability problem (\(\theta _K\)) over the static problem (\(\theta _1\)). The left graph shows the improvement after 2 h (for increasing N), while the right graph shows the time profile of the improvement of the incumbent solution in the first 60 s (for \(N = 50\))
Figure 5 illustrates the quality of the solutions obtained using the heuristic variant of our algorithm, described in Sect. 3.3, and contrasts it with the quality of the solutions obtained using the heuristic algorithm described in [13]. We make several observations from Fig. 5. First, the 2-, 3- and 4-adaptable solutions obtained using our heuristic algorithm are about 2% better than those obtained using the heuristic algorithm described in [13], on average; the differences in the qualities of the 6-, 8- and 10-adaptable solutions are smaller. Second, when compared across instances for which the exact algorithm was able to determine an optimal solution, the corresponding 2-, 3- and 4-adaptable solutions determined using our heuristic are only 0.3% suboptimal, on average. Third, 6-adaptable heuristic solutions (obtained in less than 1 min) are already better than 4-adaptable exact solutions (obtained after 2 h), for all values of N, indicating that we can compensate for not using K optimal policies by using more than K, albeit suboptimal, policies. Fourth, the figure shows that the marginal gain in objective value decreases rapidly as we increase the number of policies K. Indeed, while the 2-adaptable solutions are about 8.3% better than the 1-adaptable (i.e., static) solutions, the 10-adaptable solutions are only about 0.1% better than the 8-adaptable solutions. This is explained by the observation that the objective values of the corresponding K-adaptable solutions are very close to the optimal value of the two-stage robust optimization problem (1), as determined using the method described in [24, Remark 1].
Results for the shortest path problem using the heuristic algorithm. The graphs show the average improvement after 1 min obtained using the heuristic variant of our algorithm (left) and the heuristic algorithm described in [13] (right)
4.2 Capital budgeting
We consider the capital budgeting problem from [24], where a company wishes to invest in a subset of N projects. Each project i has an uncertain cost \(c_i (\varvec{\xi })\) and an uncertain profit \(r_i (\varvec{\xi })\) that are governed by factor models of the form
In these models, \(c_i^0\) and \(r_i^0\) represent the nominal cost and the nominal profit of project i, respectively, while \(\varvec{\varPhi }_i^\top \) and \(\varvec{\varPsi }_i^\top \) represent the ith row vectors of the factor loading matrices \(\varvec{\varPhi }, \varvec{\varPsi } \in \mathbb {R}^{N \times 4}\). The realizations of the uncertain vector of risk factors \(\varvec{\xi }\) belong to the uncertainty set \(\varXi = [-1, 1]^4\).
The company can invest in a project either before or after observing the risk factors \(\varvec{\xi }\). In the latter case, the company generates only a fraction \(\kappa \) of the profit (reflecting a penalty for postponement) but incurs the same cost as in the case of an early investment. Given an investment budget B, the capital budgeting problem can then be formulated as the following instance of the two-stage robust optimization problem (1):
where \({\mathcal {X}} = {\mathcal {Y}} = \{0, 1\}^N\).
For our numerical experiments, we randomly generate 100 instances for each problem size \(N \in \{5, 10, \ldots , 30\}\) as follows. The nominal costs \(\varvec{c}^0\) are chosen uniformly at random from the hyperrectangle \([0, 10]^N\). We then set \(\varvec{r}^0 = \varvec{c}^0 / 5\), \(B = {\mathbf {e}}^\top \varvec{c}^0 / 2\) and \(\kappa = 0.8\). The rows of the factor loading matrices \(\varvec{\varPhi }\) and \(\varvec{\varPsi }\) are sampled uniformly from the unit simplex in \(\mathbb {R}^4\); that is, the ith row vector is sampled from \([0, 1]^4\) such that \(\varvec{\varPhi }_{i}^\top {\mathbf {e}} = \varvec{\varPsi }_{i}^\top {\mathbf {e}} = 1\) is satisfied for all \(i = 1, \ldots , N\).
Results for the capital budgeting problem. The top (bottom) graphs are for the exact (heuristic) algorithm under a time limit of 2 h (1 min). The left graphs show the average improvement at the time limit (for increasing N), while the right graphs show the time profile of the improvement of the incumbent solution in the first 60 s (for \(N = 30\))
Table 3 summarizes the numerical performance of our branch-and-bound scheme for \(K \in \{2, 3, 4\}\). Table 3 demonstrates that our branch-and-bound scheme performs very well for this problem class since the majority of instances is solved to optimality for \(K \in \{2, 3\}\). Moreover, the optimality gaps for the unsolved instances are less than 4% for \(K \in \{2, 3\}\) and less than 9% for \(K = 4\) on average. Additionally, Fig. 6 shows that even for the largest instances, high-quality incumbent solutions which significantly improve (\(\approx \) 100%) upon the static robust solutions are obtained within 1 minute of computation time. In obtaining the results of Fig. 6c, d using our heuristic, we observed that limiting the computation time to 1 minute is often insufficient for the successful termination of the algorithm. Therefore, the kth second-stage policy determined by the algorithm is not always deterministic, and it can affect the solution of the \((k+1)\)-adaptability problem as well as the resulting objective value improvements. To eliminate this random effect, we ran our heuristic 10 times for each instance, using different random seeds for the underlying MILP solver, and report the averaged results in Fig. 6c, d. Our results compare favorably with those of [24] as well as those of the partition-and-bound approach for the corresponding two-stage robust optimization problem presented in [6].
4.3 Capital budgeting with loans
We consider a generalization of the capital budgeting problem from Sect. 4.2 where the company can increase its investment budget by purchasing a loan from the bank at a unit cost of \(\lambda > 0\) before the risk factors \(\varvec{\xi }\) are observed as well as purchasing a loan at a unit cost of \(\mu \lambda \) (with \(\mu > 1\)) after the observation occurs. If the company does not purchase any loan, then the problem reduces to the one described in Sect. 4.2. Therefore, we expect the worst-case profits to be at least as large as in that setting. The generalized capital budgeting problem can be formulated as the following instance of problem (1):
Here, \({\mathcal {X}} = {\mathcal {Y}} = \mathbb {R}_{+} \times \{0, 1\}^N\). The constraint \(\varvec{c} (\varvec{\xi })^\top \varvec{x} \le B + x_0\) ensures that the first-stage expenditures \(\varvec{c} (\varvec{\xi })^\top \varvec{x} \) are fully covered by the budget B as well as the loan \(x_0\) taken here-and-now.
We consider problems with \(N \in \{5, 10, \ldots , 30\}\) projects. For each value of N, we solve the same 100 instances from Sect. 4.2 with \(\lambda = 0.12\) and \(\mu = 1.2\). Table 4 shows the computational performance of our branch-and-bound scheme for \(K \in \{2, 3, 4\}\). As in the case of the problems discussed so far, the numerical tractability of our algorithm decreases as the value of K increases. However, a comparison of Tables 3 and 4 suggests that the numerical tractability is not significantly affected by the presence of the additional continuous variables \(x_0\) and \(y_0\). Indeed, the majority of instances for \(K = 2\) are solved to optimality and the average gap across all unsolved instances is less than 5% for \(K=3\) and less than 9% for \(K=4\). Figure 7 shows that the 4-adaptable solutions improve upon the static solutions by as much as 115% in the largest instances. Although not shown in the figure, a comparison of the objective values of the final incumbent solutions with those of the capital budgeting problem without loans (Sect. 4.2) reveals that for \(N \ge 15\), the option to purchase loans has no effect on the worst-case profit of the static solution and results in less than 1% improvement in the worst-case profit of the 2-adaptable solution. Indeed, the option to purchase loans results in significantly better worst-case profits only if \(K \ge 3\). The average relative gain in objective value is 4.3% for \(K=3\) and 5.9% for \(K=4\).
Results for the capital budgeting problem with loans. The graphs have the same interpretation as in Fig. 6
4.4 Project management
We define a project as a directed acyclic graph \(G = (V, A)\) whose nodes \(V = \{ 1, \ldots , N \}\) represent the tasks (e.g., ‘build foundations’ or ‘develop prototype’) and whose arcs \(A \subseteq V \times V\) denote the temporal precedences, i.e., \((i, j) \in A\) implies that task j cannot be started before task i has been completed. We assume that each task \(i \in V\) has an uncertain duration \(d_i (\varvec{\xi })\) that depends on the realization of an uncertain parameter vector \(\varvec{\xi } \in \varXi \). Without loss of generality, we stipulate that the project graph G has the unique sink \(N \in V\), and that the last task N has a duration of zero. This can always be achieved by introducing dummy nodes and/or arcs.
In the following, we want to calculate the worst-case makespan of the project, i.e, the smallest amount of time that is required to complete the project under the worst realization of the parameter vector \(\varvec{\xi } \in \varXi \). This problem can be cast as the following instance of problem (1):
Here \({\mathcal {Y}} = \mathbb {R}^N_+\), and \(y_i\) denotes the start time of task i, \(i = 1, \ldots , N\). This problem is known to be NP-hard [37, Theorem 2.1], and we will employ affine decision rules as well as K-adaptable constant and affine decisions to approximate the optimal value of this problem. Note that the problem does not contain any first-stage decisions, but such decisions could be readily included, for example, to allow for resource allocations that affect the task durations.
For our numerical experiments, we consider the instance class presented in [37, Example 2.2]. To this end, we set \(N = 3m + 1\) and \(A = \{ (3l + 1, 3l + p), (3l + p, 3l + 4) \, : \, l = 0, \ldots , m \text { and } p = 2, 3 \}\), \(d_{3l+2} (\varvec{\xi }) = \xi _{l+1}\) and \(d_{3l+3} (\varvec{\xi }) = 1 - \xi _{l+1}\), \(l = 0, \ldots , m - 1\), as well as \(d_{3l+1} (\varvec{\xi }) = 0\), \(l = 0, \ldots , m\). Figure 8 illustrates the project network corresponding to \(m = 4\). Similar to [37], we consider the uncertainty set \(\varXi = \{ \varvec{\xi } \in \mathbb {R}^m_+ \, : \, ||\varvec{\xi } - {\mathbf {e}} / 2 ||_1 \le 1/2 \}\).
Results for the project management problem. The left (right) graphs show results for the piecewise constant (affine) K-adaptability problems for increasing values of N. Graphs a and b depict improvements in objective value, while graphs c and d show optimality gaps after 2 h. The y-axes in graphs a and b have the same interpretation as those in Fig. 4 while the y-axes in graphs c and d have the same interpretation as the column “Gap (%)” in Table 2
We consider project networks of size \(N \in \{ 3 m + 1 \, : \, m = 3, 4, \ldots , 8 \}\). One can show that for each network size N, the optimal value of the corresponding static robust optimization problem as well as the affine decision rule problem is m, while the optimal value of the unapproximated two-stage robust optimization problem is \((m+1)/2\), see [37, Example 2.2]. For \(K \in \{2, 3, 4\}\), Fig. 9 summarizes the computational performance of the branch-and-bound scheme and the improvement in objective value of the resulting piecewise constant and piecewise affine decision rules with K pieces over the corresponding 1-adaptable solutions. Figure 9a, b show that using only two pieces, piecewise constant decision rules can improve upon the affine approximation by more than 12%, while a piecewise affine decision rule can improve by more than 15%. Figure 9c, d show that piecewise constant decision rules require smaller computation times than piecewise affine decision rules. This is not surprising since piecewise constant decision rules are parameterized by \({\mathcal {O}} (KN)\) variables, whereas piecewise affine decision rules are parameterized by \({\mathcal {O}} (KN^2)\) variables.
4.5 Vehicle routing
We consider the classical capacitated vehicle routing problem [21, 22, 35] defined on a complete, undirected graph \(G = (V, E)\) with nodes \(V = \{0, 1, \ldots , N\}\) and edges \(E = \{(i,j) \in V \times V: i < j \}\). Node 0 represents the unique depot, while each node \(i \in V_C = \{1, \ldots , N\}\) corresponds to a customer with demand \(d_i \in \mathbb {R}_{+}\). The depot is equipped with M homogeneous vehicles; each vehicle has capacity C and it incurs an uncertain travel time \(t_{ij}(\varvec{\xi }) = (1 + \xi _{ij}/2) t_{ij}^0\) when it traverses the edge \((i, j) \in E\). Here, \(t_{ij}^0 \in \mathbb {R}_{+}\) represents the nominal travel time along the edge \((i, j) \in E\), while \(\xi _{ij}\) denotes the uncertain deviation from the nominal value. Similar to the shortest path problem from Sect. 4.1, the realizations of the uncertain vector \(\varvec{\xi }\) are known to belong to the set
which stipulates that at most \(\varGamma \) travel times may maximally deviate from their nominal values.
A route plan\((R_1, \ldots , R_M)\) corresponds to a partition of the customer set \(V_C\) into M vehicle routes, \(R_m = (R_{m,1},\ldots , R_{m,N_m})\), where \(R_{m,l}\) represents the lth customer and \(N_m\) the number of customers served by the mth vehicle. This route plan is feasible if the total demand served on each route is less than the vehicle capacity; that is, if \(\sum _{l = 1}^{N_m} d_{R_{m,l}} \le C\) is satisfied for all \(m \in \{1, \ldots , M\}\). The total travel time of a feasible route plan under the uncertainty realization \(\varvec{\xi }\) is given by \(\sum _{m = 1}^M \sum _{l = 0}^{N_m} t_{R_{m,l} R_{m,l+1}} (\varvec{\xi })\), where we define \(R_{m,0} = R_{m,N_m+1} = 0\); that is, each vehicle starts and ends at the depot. The decision-maker aims to choose K route plans here-and-now, i.e., before observing the actual travel times, such that the worst-case total travel time of the shortest among the chosen route plans is minimized. This problem can be formulated as an instance of the K-adaptability problem (2):
Here, \({\mathcal {Y}}\) denotes the set of all feasible route plans in G; that is,
Similar to the shortest path problem, the K-adaptability formulation of the vehicle routing problem only contains second-stage decisions, and as such, the corresponding two-stage robust optimization problem (1) is of limited interest in practice. However, the K-adaptability problem (2) has important applications in logistics enterprises, where the time available between observing the travel times in a road network and determining the route plan is limited, or because the drivers must be trained to a small set of route plans that are to be executed daily over the course of a year.
Results for the vehicle routing problem. The graphs show the average improvement after 2 h obtained using the heuristic variant of our algorithm (left) and the heuristic algorithm in [13] (right)
We note that the set \({\mathcal {Y}}\) represents the so-called two-index vehicle flow formulation of the vehicle routing problem, in which the first equation ensures that M vehicles are used; the second set of equations ensures that each customer is visited by exactly one vehicle; while the third set of inequalities ensure that there are no subtours disconnected from the depot and that all vehicle capacities are respected. This formulation is known to be extremely challenging to solve because it consists of an exponential number of inequalities. For \(K > 1\), the corresponding K-adaptability problem is naturally even more challenging and it is practically intractable to solve it using the approach described in [24]. In contrast, the heuristic variant of our algorithm described in Sect. 3.3 as well as the heuristic approach of [13] only require the solution of vehicle routing subproblems that are of similar complexity as the associated 1-adaptability problems. Therefore, in the following, we only present results using these algorithms. In both cases, we solved all vehicle routing subproblems using the branch-and-cut algorithm described in [29].
For our numerical experiments, we consider all 49 instances from [29] with \(N \le 50\), which are commonly used to benchmark vehicle routing algorithms. We set an overall time limit of 2 h. For the heuristic variant of our algorithm, we further set a time limit of 10 min per vehicle routing subproblem. We note that the heuristic of [13] requires the successful termination of an expensive preprocessing step to determine good K-adaptable solutions. Therefore, to prevent bias in favor of our algorithm, Fig. 10 compares the two algorithms only across the 39 instances for which this step terminated successfully. The figure shows that when the number of policies is small, the K-adaptable solutions obtained using our algorithm are about 1% better than those obtained using the heuristic algorithm of [13]. Moreover, the differences in their objective values are relatively higher for larger instances.
5 Conclusions
In contrast to single-stage robust optimization problems, which are typically solved via monolithic reformulations, there is growing evidence that two-stage and multi-stage robust optimization problems are best solved algorithmically [6,7,8, 31, 39]. Our findings in this paper appear to confirm this observation, as our proposed branch-and-bound algorithm compares favorably with the reformulations proposed in [24]. In terms of modeling flexibility, our algorithm can accommodate mixed continuous and discrete decisions in both stages, can incorporate discrete uncertainty, and allows us to model flexible piecewise affine decision rules. At the same time, our numerical results indicate that the algorithmic approach is highly competitive in terms of computational performance as well. From a practical viewpoint, a notable feature of our algorithm is that it admits a lightweight implementation by integrating it into the branch-and-bound schemes of commercial solvers via branch callbacks, while allowing easy modification as a heuristic for large-scale instances.
Our results open up multiple fruitful avenues for future research. The scope of the presented algorithm can be broadened further by generalizing it to two-stage distributionally robust optimization problems, where the uncertain problem parameters are modeled as random variables following a probability distribution that is only partially known. More ambitiously, it would be instructive to explore how the concept of K-adaptability, as well as our proposed branch-and-bound algorithm, extend to dynamic robust optimization problems with more than two stages.
References
Ayoub, J., Poss, M.: Decomposition for adjustable robust linear optimization subject to uncertainty polytope. Comput. Manag. Sci. 13(2), 219–239 (2016)
Ben-Tal, A., Ghaoui, L.E., Nemirovski, A.: Robust Optimization. Princeton University Press, Princeton (2009)
Ben-Tal, A., Goryashko, A., Guslitzer, E., Nemirovski, A.: Adjustable robust solutions of uncertain linear programs. Math. Program. 99(2), 351–376 (2004)
Bertsimas, D., Brown, D.B., Caramanis, C.: Theory and applications of robust optimization. SIAM Rev. 53(3), 464–501 (2011)
Bertsimas, D., Caramanis, C.: Finite adaptibility in multistage linear optimization. IEEE Trans. Autom. Control 55(12), 2751–2766 (2010)
Bertsimas, D., Dunning, I.: Multistage robust mixed integer optimization with adaptive partitions. Oper. Res. 64(4), 980–998 (2016)
Bertsimas, D., Georghiou, A.: Design of near optimal decision rules in multistage adaptive mixed-integer optimization. Oper. Res. 63(3), 610–627 (2015)
Bertsimas, D., Georghiou, A.: Binary decision rules for multistage adaptive mixed-integer optimization. Math. Program. 167(2), 395–433 (2018)
Bertsimas, D., Goyal, V., Sun, X.A.: A geometric characterization of the power of finite adaptability in multistage stochastic and adaptive optimization. Math. Oper. Res. 36(1), 24–54 (2011)
Bertsimas, D., Litvinov, E., Sun, X.A., Zhao, J., Zheng, T.: Adaptive robust optimization for the security constrained unit commitment problem. IEEE Trans. Power Syst. 28(1), 52–63 (2013)
Blankenship, J.W., Falk, J.E.: Infinitely constrained optimization problems. J. Optim. Theory Appl. 19(2), 261–281 (1976)
Buchheim, C., Kurtz, J.: Min-max-min robustness: a new approach to combinatorial optimization under uncertainty based on multiple solutions. Electron Notes Discrete Math. 52, 45–52 (2016)
Buchheim, C., Kurtz, J.: Min–max–min robust combinatorial optimization. Math. Program. 163(1), 1–23 (2017)
Buchheim, C., Kurtz, J.: Complexity of min-max-min robustness for combinatorial optimization under discrete uncertainty. Discrete Optim. 28(1), 1–15 (2018)
Chen, X., Zhang, Y.: Uncertain linear programs: extended affinely adjustable robust counterparts. Oper. Res. 57(6), 1469–1482 (2009)
Gabrel, V., Murat, C., Thiele, A.: Recent advances in robust optimization: an overview. Eur. J. Oper. Res. 235(3), 471–483 (2014)
Georghiou, A., Wiesemann, W., Kuhn, D.: Generalized decision rule approximations for stochastic programming via liftings. Math. Program. 152(1), 301–338 (2015)
Goh, J., Sim, M.: Distributionally robust optimization and its tractable approximations. Oper. Res. 58(4), 902–917 (2010)
Gorissen, B.L., den Hertog, D.: Robust counterparts of inequalities containing sums of maxima of linear functions. Eur. J. Oper. Res. 227(1), 30–43 (2013)
Gorissen, B.L., Yanıkoğlu, I., den Hertog, D.: A practical guide to robust optimization. Omega 53, 124–137 (2015)
Gounaris, C., Repoussis, P., Tarantilis, C., Wiesemann, W., Floudas, C.: An adaptive memory programming framework for the robust capacitated vehicle routing problem. Transp. Sci. 50(4), 1239–1260 (2016)
Gounaris, C., Wiesemann, W., Floudas, C.: The robust capacitated vehicle routing problem under demand uncertainty. Oper. Res. 61(3), 677–693 (2013)
Guslitser, E.: Uncertainty-immunized solutions in linear programming. Master’s Thesis, Technion, Israeli Institute of Technology (2002)
Hanasusanto, G.A., Kuhn, D., Wiesemann, W.: \(K\)-adaptability in two-stage robust binary programming. Oper. Res. 63(4), 877–891 (2015)
IBM: ILOG CPLEX Optimizer (2018). https://www-01.ibm.com/software/commerce/optimization/cplex-optimizer/. Accessed 27 July 2018
Jiang, R., Zhang, M., Li, G., Guan, Y.: Two-stage robust power grid optimization problem. Available on Optimization Online (2010)
Kelley, J.E.: The cutting-plane method for solving convex programs. J. Soc. Ind. Appl. Math. 8(4), 703–712 (1960)
Kuhn, D., Wiesemann, W., Georghiou, A.: Primal and dual linear decision rules in stochastic and robust optimization. Math. Program. 130(1), 177–209 (2011)
Lysgaard, J., Letchford, A., Eglese, R.: A new branch-and-cut algorithm for the capacitated vehicle routing problem. Math. Program. 100(2), 423–445 (2004)
Mutapcic, A., Boyd, S.: Cutting-set methods for robust convex optimization with pessimizing oracles. Optim. Methods Softw. 24(3), 381–406 (2009)
Postek, K., den Hertog, D.: Multistage adjustable robust mixed-integer optimization via iterative splitting of the uncertainty set. INFORMS J. Comput. 28(3), 553–574 (2016)
Rubin, P.: When the OctoMom Solves MILPs (2010). https://orinanobworld.blogspot.com/2010/06/when-octomom-solves-milps.html. Accessed 29 Jan 2019
Subramanyam, A., Gounaris, C., Wiesemann, W.: KAdaptabilitySolver (GitHub repository) (2019). https://doi.org/10.5281/zenodo.3490004
Thiele, A., Terry, T., Epelman, M.: Robust linear optimization with recourse. Technical Report, Lehigh University and University of Michigan, (2010)
Toth, P., Vigo, D.: Vehicle routing: problems, methods, and applications. Society for Industrial and Applied Mathematics, 2nd edn. (2014)
Vayanos, P., Kuhn, D., Rustem, B.: Decision rules for information discovery in multi-stage stochastic programming. In: Proceedings of the 50th IEEE Conference on Decision and Control and European Control Conference, pp. 7368–7373 (2011)
Wiesemann, W., Kuhn, D., Rustem, B.: Robust resource allocations in temporal networks. Math. Program. 135(1), 437–471 (2012)
Yanıkoğlu, I., Gorissen, B.L., den Hertog, D.: A survey of adjustable robust optimization. Eur. J. Oper. Res. 277(3), 799–813 (2019)
Zeng, B., Zhao, L.: Solving two-stage robust optimization problems using a column-and-constraint generation method. Oper. Res. Lett. 41(5), 457–561 (2013)
Zhao, C., Wang, J., Watson, J.P., Guan, Y.: Multi-stage robust unit commitment considering wind and demand response uncertainties. IEEE Trans. Power Syst. 28(3), 2708–2717 (2013)
Zhao, L., Zeng, B.: An exact algorithm for two-stage robust optimization with mixed integer recourse problems. Technical Report, University of South Florida, (2012)
Acknowledgements
Anirudh Subramanyam gratefully acknowledges support from the John and Claire Bertucci Graduate Fellowship program at Carnegie Mellon University.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported by the National Science Foundation, Grant CMMI-1434682, and the Engineering and Physical Sciences Research Council, Grants EP/M028240/1, EP/M027856/1 and EP/N020030/1.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Subramanyam, A., Gounaris, C.E. & Wiesemann, W. K-adaptability in two-stage mixed-integer robust optimization. Math. Prog. Comp. 12, 193–224 (2020). https://doi.org/10.1007/s12532-019-00174-2
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12532-019-00174-2