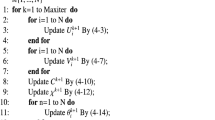Alternating proximal gradient method for sparse nonnegative Tucker decomposition

Abstract

Multi-way data arises in many applications such as electroencephalography classification, face recognition, text mining and hyperspectral data analysis. Tensor decomposition has been commonly used to find the hidden factors and elicit the intrinsic structures of the multi-way data. This paper considers sparse nonnegative Tucker decomposition (NTD), which is to decompose a given tensor into the product of a core tensor and several factor matrices with sparsity and nonnegativity constraints. An alternating proximal gradient method is applied to solve the problem. The algorithm is then modified to sparse NTD with missing values. Per-iteration cost of the algorithm is estimated scalable about the data size, and global convergence is established under fairly loose conditions. Numerical experiments on both synthetic and real world data demonstrate its superiority over a few state-of-the-art methods for (sparse) NTD from partial and/or full observations. The MATLAB code along with demos are accessible from the author’s homepage.

Appendices

Appendix A: Efficient computation

The most expensive step in Algorithm 1 is the computation of $\nabla _{\varvec{\mathcal {C}}}\ell (\varvec{\mathcal {C}}, \mathbf {A})$ and $\nabla _{\mathbf {A}_n}\ell (\varvec{\mathcal {C}}, {\mathbf {A}})$ in (12) and (13), respectively. Note that we have omitted the superscript. Next, we discuss how to efficiently compute them.

1.1 Computation of $\nabla _{\varvec{\mathcal {C}}}\ell$

According to (2), we have

$$\begin{aligned} \ell (\varvec{\mathcal {C}},\mathbf {A})=\frac{1}{2}\big \Vert \big (\otimes _{n=N}^1 \mathbf {A}_n\big )\mathrm {vec}(\varvec{\mathcal {C}})-\mathrm {vec}(\varvec{\mathcal {M}})\big \Vert _2^2. \end{aligned}$$

Using the properties of Kronecker product (see [14], for example), we have

$$\begin{aligned} \mathrm {vec}\big (\nabla _{\varvec{\mathcal {C}}}\ell (\varvec{\mathcal {C}},\mathbf {A})\big )=\big (\otimes _{n=N}^1\mathbf {A}_n^\top \mathbf {A}_n\big )\mathrm {vec}(\varvec{\mathcal {C}})-\big (\otimes _{n=N}^1\mathbf {A}_n^\top \big )\mathrm {vec}(\varvec{\mathcal {M}}). \end{aligned}$$

(34)

It is extremely expensive to explicitly reformulate the Kronecker products in (34). Fortunately, we can use (2) again to have

$$\begin{aligned} \big (\otimes _{n=N}^1\mathbf {A}_n^\top \mathbf {A}_n\big )\mathrm {vec}(\varvec{\mathcal {C}})= \mathrm {vec}\big (\varvec{\mathcal {C}}\times _1\mathbf {A}_1^\top \mathbf {A}_1\cdots \times _N \mathbf {A}_N^\top \mathbf {A}_N\big ) \end{aligned}$$

and

$$\begin{aligned} \big (\otimes _{n=N}^1\mathbf {A}_n^\top \big )\mathrm {vec}(\varvec{\mathcal {M}})= \mathrm {vec}\big (\varvec{\mathcal {M}}\times _1\mathbf {A}_1^\top \cdots \times _N\mathbf {A}_N^\top \big ). \end{aligned}$$

Hence, we have from (34) and the above two equalities that

$$\begin{aligned} \nabla _{\varvec{\mathcal {C}}}\ell (\varvec{\mathcal {C}},\mathbf {A})=\varvec{\mathcal {C}}\times _1\mathbf {A}_1^\top \mathbf {A}_1\cdots \times _N \mathbf {A}_N^\top \mathbf {A}_N-\varvec{\mathcal {M}}\times _1\mathbf {A}_1^\top \cdots \times _N\mathbf {A}_N^\top . \end{aligned}$$

(35)

1.2 Computation of $\nabla _{\mathbf {A}_n}\ell$

According to (4), we have

$$\begin{aligned} \ell (\varvec{\mathcal {C}},\mathbf {A})=\frac{1}{2}\big \Vert \mathbf {A}_n\mathbf {C}_{(n)} \left( \otimes _{\begin{array}{c} i=N\\ i\ne n \end{array}}^1\mathbf {A}_i\right) ^\top -\mathbf {M}_{(n)}\big \Vert _F^2. \end{aligned}$$

(36)

Hence,

$$\begin{aligned} \nabla _{\mathbf {A}_n}\ell (\varvec{\mathcal {C}},\mathbf {A})=\mathbf {A}_n(\mathbf {B}_n\mathbf {B}_n^\top )- \mathbf {M}_{(n)}\mathbf {B}_n^\top \end{aligned}$$

(37)

where

$$\begin{aligned} \mathbf {B}_n=\mathbf {C}_{(n)}\left( \!\!\otimes _{\begin{array}{c} i=N\\ i\ne n \end{array}}^1\mathbf {A}_i\right) ^\top . \end{aligned}$$

(38)

Similar to what has been done to (34), we do not explicitly reformulate the Kronecker product in (38) but let

$$\begin{aligned} \varvec{\mathcal {X}}=\varvec{\mathcal {C}}\times _1\mathbf {A}_1\cdots \times _{n-1}\mathbf {A}_{n-1}\times _{n+1} \mathbf {A}_{n+1}\cdots \times _N\mathbf {A}_N. \end{aligned}$$

(39)

Then we have $\mathbf {B}_n=\mathbf {X}_{(n)}$ according to (4).

Appendix B: Complexity analysis of Algorithm 1

Through (35), the computation of $\nabla _{\varvec{\mathcal {C}}}\ell (\varvec{\mathcal {C}},\mathbf {A})$ requires

$$\begin{aligned} C\left( \sum _{j=1}^N R_j^2 I_j+\sum _{j=1}^NR_j\prod _{i=1}^N R_i+\sum _{j=1}^N \left( \prod _{i=1}^j R_i \right) \left( \prod _{i=j}^N I_i \right) \right) \end{aligned}$$

(40)

flops, where $C\approx 2$, the first part comes from the computation of all $\mathbf {A}_i^\top \mathbf {A}_i$’s, and the second and third parts are respectively from the computations of the first and second terms in (35). Disregarding¹² the time for unfolding a tensor and using (37), we have the cost for $\nabla _{\mathbf {A}_n}\ell (\varvec{\mathcal {C}},\mathbf {A})$ to be

$$\begin{aligned}&C\left( \underset{\text {part 1}}{\underbrace{\sum _{j=1}^{n-1}\left( \prod _{i=1}^jI_i \right) \left( \prod _{i=j}^N R_i\right) +R_n\left( \prod _{i=1}^{n-1}I_i \right) \sum _{j=n+1}^N \left( \prod _{i=n+1}^jI_i \right) \left( \prod _{i=j}^NR_i\right) }}\right. \nonumber \\&\qquad \quad \left. +\underset{\text {part 2}}{\underbrace{R_n^2\prod _{i\ne n}I_i+R_n^2I_n}}+\underset{\text {part 3}}{\underbrace{R_n\prod _{i=1}^NI_i}}\right) , \end{aligned}$$

(41)

where $C$ is the same as that in (40), “part 1” is for the computation of $\mathbf {B}_n$ via (39), “part 2” and “part 3” are respectively from the computations of the first and second terms in (37).

Suppose $R_i<I_i$ for all $i=1,\ldots ,N$. Then the quantity of (40) is dominated by the third part because in this case,

$$\begin{aligned} R_j^2I_j<\left( \prod _{i=1}^j R_i \right) \left( \prod _{i=j}^N I_i \right) ,\qquad R_j\prod _{i=1}^N R_i< \left( \prod _{i=1}^j R_i \right) \left( \prod _{i=j}^N I_i \right) . \end{aligned}$$

The quantity of (41) is dominated by the first and third parts. Only taking account of the dominating terms, we claim that the quantities of (40) and (41) are similar. To see this, assume $R_i=R, I_i=I,$ for all $i$’s. Then the third part of (40) is $\sum _{j=1}^NR^jI^{N-j+1}$, and the sum of the first and third parts of (41) is

$$\begin{aligned}&\sum _{j=1}^{n-1} \left( \prod _{i=1}^jI_i \right) \left( \prod _{i=j}^N R_i \right) +R_n \left( \prod _{i=1}^{n-1}I_i \right) \sum _{j=n+1}^N \left( \prod _{i=n+1}^jI_i\right) \left( \prod _{i=j}^NR_i \right) +R_n\prod _{i=1}^NI_i\\&\quad =\sum _{j=1}^{n-1}I^jR^{N-j+1}+\sum _{j=n+1}^N I^{j-1}R^{N-j+2}+RI^N\\&\quad =\sum _{j=N-n+2}^NR^jI^{N-j+1}+\sum _{j=2}^{N-n+1}R^jI^{N-j+1}+RI^N\\&\quad =\sum _{j=1}^NR^jI^{N-j+1}. \end{aligned}$$

Hence, the costs for computing $\nabla _{\varvec{\mathcal {C}}}\ell (\varvec{\mathcal {C}},\mathbf {A})$ and $\nabla _{\mathbf {A}_n}\ell (\varvec{\mathcal {C}},\mathbf {A})$ are similar.

After obtaining the partial gradients $\nabla _{\varvec{\mathcal {C}}}\ell (\varvec{\mathcal {C}},\mathbf {A})$ and $\nabla _{\mathbf {A}_n}\ell (\varvec{\mathcal {C}},\mathbf {A})$, it remains to do some projections to nonnegative orthant to finish the updates in (12) and (13), and the cost is proportional to the size of $\varvec{\mathcal {C}}$ and $\mathbf {A}_n$, i.e., $C_p\prod _{i=1}^NR_i$ and $C_pI_nR_n$ with $C_p\approx 4$. The data fitting term can be evaluated by

$$\begin{aligned} \ell (\varvec{\mathcal {C}},\mathbf {A})=\frac{1}{2}\left( \langle \mathbf {A}_n^\top \mathbf {A}_n, \mathbf {B}_n\mathbf {B}_n^\top \rangle -2\langle \mathbf {A}_n, \mathbf {M}_{(n)}\mathbf {B}_n^\top \rangle +\Vert \varvec{\mathcal {M}}\Vert _F^2\right) \!, \end{aligned}$$

where $\mathbf {B}_n$ is defined in (38). Note that $\mathbf {A}_n^\top \mathbf {A}_n$, $\mathbf {B}_n\mathbf {B}_n^\top$ and $\mathbf {M}_{(n)}\mathbf {B}_n^\top$ have been obtained during the computation of $\nabla _{\varvec{\mathcal {C}}}\ell (\varvec{\mathcal {C}},\mathbf {A})$ and $\nabla _{\mathbf {A}_n}\ell (\varvec{\mathcal {C}},\mathbf {A})$, and $\Vert \varvec{\mathcal {M}}\Vert _F^2$ can be pre-computed before running the algorithm. Hence, we need $C(R_n^2+I_nR_n)$ additional flops to evaluate $\ell (\varvec{\mathcal {C}},\mathbf {A})$, where $C\approx 2$. To get the objective value, we need $C(\prod _{i=1}^NR_i+\sum _{i=1}^NI_iR_i)$ more flops for the regularization terms.

Some more computations occur in choosing Lipschitz constants $L_c$ and $L_n$’s. When $R_n\ll I_n$ for all $n$, the cost for computing Lipschitz constants, projection to nonnegative orthant and objective evaluation is negligible compared to that for computing partial gradients $\nabla _{\varvec{\mathcal {C}}}\ell (\varvec{\mathcal {C}},\mathbf {A})$ and $\nabla _{\mathbf {A}_n}\ell (\varvec{\mathcal {C}},\mathbf {A})$. Omitting the negligible cost and only accounting the main cost in (40) and (41), the per-iteration complexity of Algorithm 1 is

$$\begin{aligned} N\cdot \mathcal {O}\left( \sum _{j=1}^N \left( \prod _{i=1}^j R_i \right) \left( \prod _{i=j}^N I_i\right) +\sum _{j=1}^N \left( \prod _{i=1}^j I_i\right) \left( \prod _{i=j}^N R_i \right) \right) . \end{aligned}$$

(42)

Appendix C: Proof of Theorem 1

1.1 Subsequence convergence

First, we give a subsequence convergence result, namely, any limit point of $\{\varvec{\mathcal {W}}^k\}$ is a stationary point. Using Lemma 2.1 of [34], we have

$$\begin{aligned}&F(\varvec{\mathcal {C}}^{k,n-1},\mathbf {A}_{j<n}^k,\mathbf {A}_{j\ge n}^{k-1})-F(\varvec{\mathcal {C}}^{k,n},\mathbf {A}_{j<n}^k,\mathbf {A}_{j\ge n}^{k-1})\nonumber \\&\quad \ge \frac{L_c^{k,n}}{2}\Vert \hat{\varvec{\mathcal {C}}}^{k,n}-\varvec{\mathcal {C}}^{k,n}\Vert _F^2+L_c^{k,n} \left\langle \hat{\varvec{\mathcal {C}}}^{k,n}-\varvec{\mathcal {C}}^{k,n-1}, \varvec{\mathcal {C}}^{k,n}-\hat{\varvec{\mathcal {C}}}^{k,n}\right\rangle \nonumber \\&\quad =\frac{L_c^{k,n}}{2}\Vert \varvec{\mathcal {C}}^{k,n-1}-\varvec{\mathcal {C}}^{k,n}\Vert _F^2- \frac{L_c^{k,n}}{2}(\omega _c^{k,n})^2\Vert \varvec{\mathcal {C}}^{k,n-2}- \varvec{\mathcal {C}}^{k,n-1}\Vert _F^2\end{aligned}$$

(43)

$$\begin{aligned}&\quad \ge \frac{L_c^{k,n}}{2}\Vert \varvec{\mathcal {C}}^{k,n-1}- \varvec{\mathcal {C}}^{k,n}\Vert _F^2-\frac{L_c^{k,n-1}}{2} \delta _\omega ^2\Vert \varvec{\mathcal {C}}^{k,n-2}- \varvec{\mathcal {C}}^{k,n-1}\Vert _F^2, \end{aligned}$$

(44)

where we have used $\omega _c^{k,n}\le \delta _\omega \sqrt{\frac{L_c^{k,n-1}}{L_c^{k,n}}}$ to get the last inequality. Note that if the re-update in Line ReDo is performed, then $\omega _c^{k,n}=0$ in (43), and (44) still holds. Similarly, we have

$$\begin{aligned} \begin{array}{ll} &{}F(\varvec{\mathcal {C}}^{k,n},\mathbf {A}_{j<n}^k,\mathbf {A}_{j\ge n}^{k-1})-F(\varvec{\mathcal {C}}^{k,n},\mathbf {A}_{j\le n}^k,\mathbf {A}_{j> n}^{k-1})\\ &{}\quad \ge \frac{L_n^k}{2}\Vert \mathbf {A}_n^{k-1}-\mathbf {A}_n^k\Vert _F^2- \frac{L_n^{k-1}}{2}\delta _\omega ^2\Vert \mathbf {A}_n^{k-2}- \mathbf {A}_n^{k-1}\Vert _F^2. \end{array} \end{aligned}$$

(45)

Summing (44) and (45) together over $n$ and noting $\varvec{\mathcal {C}}^{k,-1}=\varvec{\mathcal {C}}^{k-1,N-1}, \varvec{\mathcal {C}}^{k,0}=\varvec{\mathcal {C}}^{k-1,N}$ yield

$$\begin{aligned}&F(\varvec{\mathcal {W}}^{k-1})-F(\varvec{\mathcal {W}}^{k})\nonumber \\&\quad \ge \sum _{n=1}^N\left( \frac{L_c^{k,n}}{2}\Vert \varvec{\mathcal {C}}^{k,n-1}- \varvec{\mathcal {C}}^{k,n}\Vert _F^2-\frac{L_c^{k,n-1}}{2} \delta _\omega ^2\Vert \varvec{\mathcal {C}}^{k,n-2}-\varvec{\mathcal {C}}^{k,n-1}\Vert _F^2\right. \nonumber \\&\quad \quad \left. +\frac{L_n^k}{2}\Vert \mathbf {A}_n^{k-1}-\mathbf {A}_n^k\Vert _F^2- \frac{L_n^{k-1}}{2}\delta _\omega ^2\Vert \mathbf {A}_n^{k-2}-\mathbf {A}_n^{k-1}\Vert _F^2 \right) \nonumber \\&\quad =\frac{L_c^{k,N}}{2}\Vert \varvec{\mathcal {C}}^{k,N-1}-\varvec{\mathcal {C}}^{k,N}\Vert _F^2- \frac{L_c^{k-1,N}}{2}\delta _\omega ^2\Vert \varvec{\mathcal {C}}^{k-1,N-1}- \varvec{\mathcal {C}}^{k-1,N}\Vert _F^2\nonumber \\&\quad \quad +\sum _{n=1}^{N-1}\frac{(1-\delta _\omega ^2)L_c^{k,n}}{2}\Vert \varvec{\mathcal {C}}^{k,n-1}-\varvec{\mathcal {C}}^{k,n}\Vert _F^2\nonumber \\&\quad \quad +\sum _{n=1}^N\left( \frac{L_n^k}{2}\Vert \mathbf {A}_n^{k-1}-\mathbf {A}_n^k\Vert _F^2- \frac{L_n^{k-1}}{2}\delta _\omega ^2\Vert \mathbf {A}_n^{k-2}- \mathbf {A}_n^{k-1}\Vert _F^2\right) . \end{aligned}$$

(46)

Summing (46) over $k$, we have

$$\begin{aligned}&F(\varvec{\mathcal {W}}^{0})-F(\varvec{\mathcal {W}}^{K})\nonumber \\&\quad \ge \sum _{k=1}^K\sum _{n=1}^N\left( \frac{(1-\delta _\omega ^2) L_c^{k,n}}{2}\Vert \varvec{\mathcal {C}}^{k,n-1}-\varvec{\mathcal {C}}^{k,n}\Vert _F^2+ \frac{(1-\delta _\omega ^2)L_n^{k}}{2}\Vert \mathbf {A}_n^{k-1}-\mathbf {A}_n^k\Vert _F^2 \right) \nonumber \\&\quad \ge \frac{(1-\delta _\omega ^2)L_d}{2}\sum _{k=1}^K\sum _{n=1}^N \left( \Vert \varvec{\mathcal {C}}^{k,n-1}-\varvec{\mathcal {C}}^{k,n}\Vert _F^2+\Vert \mathbf {A}_n^{k-1}- \mathbf {A}_n^k\Vert _F^2\right) . \end{aligned}$$

(47)

Letting $K\rightarrow \infty$ and observing $F$ is lower bounded, we have

$$\begin{aligned} \sum _{k=1}^\infty \sum _{n=1}^N\left( \Vert \varvec{\mathcal {C}}^{k,n-1}- \varvec{\mathcal {C}}^{k,n}\Vert _F^2+\Vert \mathbf {A}_n^{k-1}-\mathbf {A}_n^k\Vert _F^2\right) <\infty . \end{aligned}$$

(48)

Suppose $\bar{\varvec{\mathcal {W}}}=(\bar{\varvec{\mathcal {C}}},\bar{\mathbf {A}}_1,\ldots ,\bar{\mathbf {A}}_N)$ is a limit point of $\{\varvec{\mathcal {W}}^k\}$. Then there is a subsequence $\{\varvec{\mathcal {W}}^{k'}\}$ converging to $\bar{\varvec{\mathcal {W}}}$. Since $\{L_c^{k,n},L_n^k\}$ is bounded, passing another subsequence if necessary, we assume $L_c^{k',n}\rightarrow \bar{L}_c^n$ and $L_n^{k'}\rightarrow \bar{L}_n$. Note that (48) implies $\mathbf {A}^{k'-1}\rightarrow \bar{\mathbf {A}}$ and $\varvec{\mathcal {C}}^{m,n}\rightarrow \bar{\varvec{\mathcal {C}}}$ for all $n$ and $m=k',k'-1,k'-2$, as $k\rightarrow \infty$. Hence, $\hat{\varvec{\mathcal {C}}}^{k',n}\rightarrow \bar{\varvec{\mathcal {C}}}$ for all $n$, as $k\rightarrow \infty$. Recall that

$$\begin{aligned} \varvec{\mathcal {C}}^{k',n}&= \mathop {\hbox {argmin}}\limits _{\varvec{\mathcal {C}}\ge 0}\left\langle \nabla _{\varvec{\mathcal {C}}} \ell (\hat{\varvec{\mathcal {C}}}^{k',n},\mathbf {A}_{j<n}^{k'},\mathbf {A}_{j\ge n}^{k'-1}),\varvec{\mathcal {C}}-\hat{\varvec{\mathcal {C}}}^{k',n} \right\rangle \nonumber \\&+\frac{L_c^{k',n}}{2}\Vert \varvec{\mathcal {C}}- \hat{\varvec{\mathcal {C}}}^{k',n}\Vert _F^2+\lambda _c\Vert \varvec{\mathcal {C}}\Vert _1. \end{aligned}$$

(49)

Letting $k\rightarrow \infty$ and using the continuity of the objective in (49) give

$$\begin{aligned} \bar{\varvec{\mathcal {C}}}=\hbox {argmin}_{\varvec{\mathcal {C}}\ge 0}\left\langle \nabla _{\varvec{\mathcal {C}}} \ell (\bar{\varvec{\mathcal {C}}},\bar{\mathbf {A}}),\varvec{\mathcal {C}}- \bar{\varvec{\mathcal {C}}}\right\rangle +\frac{\bar{L}_c^{n}}{2}\Vert \varvec{\mathcal {C}}- \bar{\varvec{\mathcal {C}}}\Vert _F^2+\lambda _c\Vert \varvec{\mathcal {C}}\Vert _1. \end{aligned}$$

Hence, $\bar{\varvec{\mathcal {C}}}$ satisfies the first-order optimality condition

$$\begin{aligned} \left\langle \nabla _{\varvec{\mathcal {C}}} \ell (\bar{\varvec{\mathcal {C}}},\bar{\mathbf {A}})+\lambda _c\varvec{\mathcal {P}}_c, \varvec{\mathcal {C}}-\bar{\varvec{\mathcal {C}}}\right\rangle \ge 0,~\text {for all }\varvec{\mathcal {C}}\ge 0, \text { some }\varvec{\mathcal {P}}_c\in \partial \Vert \bar{\varvec{\mathcal {C}}}\Vert _1. \end{aligned}$$

(50)

Similarly, we have for all $n$ that

$$\begin{aligned} \left\langle \nabla _{\mathbf {A}_n} \ell (\bar{\varvec{\mathcal {C}}},\bar{\mathbf {A}})+\lambda _n\varvec{\mathbf {P}}_n, \mathbf {A}_n-\bar{\mathbf {A}}_n\right\rangle \ge 0,~\text {for all }\mathbf {A}_n\ge 0, \text { some }\varvec{\mathbf {P}}_n\in \partial \Vert \bar{\mathbf {A}}_n\Vert _1. \end{aligned}$$

(51)

Note (50) together with (51) gives the first-order optimality conditions of (5). Hence, $\bar{\varvec{\mathcal {W}}}$ is a stationary point.

1.2 Global convergence

Next we show the entire sequence $\{\varvec{\mathcal {W}}^k\}$ converges to a limit point $\bar{\varvec{\mathcal {W}}}$. Since all $\lambda _c,\lambda _1,\ldots ,\lambda _N$ are positive, the sequence $\{\varvec{\mathcal {W}}^k\}$ is bounded and admits a finite limit point $\bar{\varvec{\mathcal {W}}}$. Let $E=\{\varvec{\mathcal {W}}: \Vert \varvec{\mathcal {W}}\Vert _F\le 4\nu \}$, where $\Vert \varvec{\mathcal {W}}\Vert _F\triangleq \sqrt{\Vert \varvec{\mathcal {C}}\Vert _F^2+\Vert \mathbf {A}\Vert _F^2}$ and $\nu$ is a constant such that $\Vert (\varvec{\mathcal {C}}^{k,n},\mathbf {A}^k)\Vert _F\le \nu$ for all $k,n$. Let $L_G$ be a uniform Lipschitz constant of $\nabla _{\varvec{\mathcal {C}}}\ell (\varvec{\mathcal {W}})$ and $\nabla _{\mathbf {A}_n}\ell (\varvec{\mathcal {W}}), n = 1,\ldots ,N,$ over $E$, namely,

$$\begin{aligned} \Vert \nabla _{\varvec{\mathcal {C}}}\ell (\varvec{\mathcal {Y}})-\nabla _{\varvec{\mathcal {C}}} \ell (\varvec{\mathcal {Z}})\Vert _F\le&L_G\Vert \varvec{\mathcal {Y}}-\varvec{\mathcal {Z}}\Vert _F,~\forall \varvec{\mathcal {Y}},\varvec{\mathcal {Z}}\in E,\end{aligned}$$

(52a)

$$\begin{aligned} \Vert \nabla _{\mathbf {A}_n}\ell (\varvec{\mathcal {Y}})-\nabla _{\mathbf {A}_n} \ell (\varvec{\mathcal {Z}})\Vert _F\le&L_G\Vert \varvec{\mathcal {Y}}-\varvec{\mathcal {Z}}\Vert _F,~\forall ~ \varvec{\mathcal {Y}},\varvec{\mathcal {Z}}\in E,~\forall n, \end{aligned}$$

(52b)

Let

$$\begin{aligned} H(\varvec{\mathcal {C}},\mathbf {A})=\ell (\varvec{\mathcal {C}},\mathbf {A})+\lambda _c\Vert \varvec{\mathcal {C}}\Vert _1+ \delta _+(\varvec{\mathcal {C}})+\overset{N}{\underset{n=1}{\sum }} \big (\lambda _n\Vert \mathbf {A}_n\Vert _1+\delta _+(\mathbf {A}_n)\big ) \end{aligned}$$

and

$$\begin{aligned} r_c(\varvec{\mathcal {C}})=\lambda _c\Vert \varvec{\mathcal {C}}\Vert _1+\delta _+(\varvec{\mathcal {C}}), \quad r_n(\mathbf {A}_n)=\lambda _n\Vert \mathbf {A}_n\Vert _1+\delta _+(\mathbf {A}_n),\ n=1,\ldots ,N, \end{aligned}$$

where $\delta _+(\cdot )$ is the indicator function on nonnegative orthant, namely, it equals zero if the argument is component-wise nonnegative and $+\infty$ otherwise.

Note that (5) is equivalent to

$$\begin{aligned} \min _{\varvec{\mathcal {C}},\mathbf {A}}H(\varvec{\mathcal {C}},\mathbf {A}). \end{aligned}$$

(53)

Recall that $H$ satisfies the KL property (see [4, 24] for example) at $\bar{\varvec{\mathcal {W}}}$, namely, there exist $\gamma ,\rho >0$, $\theta \in [0,1)$, and a neighborhood $B(\bar{\varvec{\mathcal {W}}},\rho )\triangleq \{\varvec{\mathcal {W}}:\Vert \varvec{\mathcal {W}}- \bar{\varvec{\mathcal {W}}}\Vert _F\le \rho \}$ such that

$$\begin{aligned} |H(\varvec{\mathcal {W}})-H(\bar{\varvec{\mathcal {W}}})|^\theta \le \gamma \cdot \text {dist}(\mathbf {0},\partial H(\varvec{\mathcal {W}})),~\text {for all }\varvec{\mathcal {W}}\in B(\bar{\varvec{\mathcal {W}}},\rho ). \end{aligned}$$

(54)

Denote $H_k=H(\varvec{\mathcal {W}}^k)-H(\bar{\varvec{\mathcal {W}}})$. Then $H_k\downarrow 0$. Since $\bar{\varvec{\mathcal {W}}}$ is a limit point of $\{\varvec{\mathcal {W}}^k\}$ and $\Vert \mathbf {A}^k-\mathbf {A}^{k+1}\Vert _F\rightarrow 0,\Vert \varvec{\mathcal {C}}^{k,n-1}-\varvec{\mathcal {C}}^{k,n}\Vert _F\rightarrow 0$ for all $k,n$ from (48), for any $T>0$, there must exist $k_0$ such that $\varvec{\mathcal {W}}^j\in B(\bar{\varvec{\mathcal {W}}},\rho ), j=k_0,k_0+1,k_0+2$ and

$$\begin{aligned}&T\big (H_{k_0}^{1-\theta }+\Vert \mathbf {A}^{k_0}-\mathbf {A}^{k_0+1}\Vert _F+\Vert \mathbf {A}^{k_0+1}-\mathbf {A}^{k_0+2}\Vert _F+\Vert \varvec{\mathcal {C}}^{k_0+2,N-1}- \varvec{\mathcal {C}}^{k_0+2,N}\Vert _F\big )\\&\quad +\Vert \varvec{\mathcal {W}}^{k_0+2}-\bar{\varvec{\mathcal {W}}}\Vert _F<\rho . \end{aligned}$$

Take $T$ as specified in (66) and consider the sequence $\{\varvec{\mathcal {W}}^k\}_{k\ge k_0}$, which is equivalent to starting the algorithm from $\varvec{\mathcal {W}}^{k_0}$ and, thus without loss of generality, let $k_0=0$, namely, $\varvec{\mathcal {W}}^j\in B(\bar{\varvec{\mathcal {W}}},\rho ), j=0,1,2$, and

$$\begin{aligned} T\big (H_{0}^{1-\theta }+\Vert \mathbf {A}^{0}-\mathbf {A}^{1}\Vert _F+\Vert \mathbf {A}^{1}- \mathbf {A}^{2}\Vert _F+\Vert \varvec{\mathcal {C}}^{2,N-1}- \varvec{\mathcal {C}}^{2,N}\Vert _F\big )+\Vert \varvec{\mathcal {W}}^{2}-\bar{\varvec{\mathcal {W}}}\Vert _F<\rho . \end{aligned}$$

(55)

The idea of our proof is to show

$$\begin{aligned} \varvec{\mathcal {W}}^k\in B(\bar{\varvec{\mathcal {W}}},\rho ),~\text {for all }k, \end{aligned}$$

(56)

and employ the KL inequality (54) to show $\{\varvec{\mathcal {W}}^k\}$ is a Cauchy sequence, thus the entire sequence converges. Assume $\varvec{\mathcal {W}}^k\in B(\bar{\varvec{\mathcal {W}}},\rho )$ for $0\le k\le K$. We go to show $\varvec{\mathcal {W}}^{K+1}\in B(\bar{\varvec{\mathcal {W}}},\rho )$ and conclude (56) by induction.

Note that

$$\begin{aligned} \partial H(\varvec{\mathcal {W}}^k)&=\left\{ \partial r_1(\mathbf {A}_1^k) +\nabla _{\mathbf {A}_1}\ell (\varvec{\mathcal {W}}^k)\right\} \times \cdots \times \left\{ \partial r_N(\mathbf {A}_N^k) +\nabla _{\mathbf {A}_N}\ell (\varvec{\mathcal {W}}^k)\right\} \\&\quad \times \left\{ \partial r_c(\varvec{\mathcal {C}}^{k,N}) +\nabla _{\varvec{\mathcal {C}}}\ell (\varvec{\mathcal {W}}^k)\right\} \!, \end{aligned}$$

and for all $n$ and $k$

$$\begin{aligned}&-L_n^k(\mathbf {A}_n^k-\hat{\mathbf {A}}_n^k)-\nabla _{\mathbf {A}_n}\ell (\varvec{\mathcal {C}}^{k,n}, \mathbf {A}_{j<n}^k,\hat{\mathbf {A}}_n^k,\mathbf {A}_{j\ge n}^{k-1})+\nabla _{\mathbf {A}_n}\ell (\varvec{\mathcal {W}}^k)\\&\quad \in \partial r_n(\mathbf {A}_n^k)+\nabla _{\mathbf {A}_n}\ell (\varvec{\mathcal {W}}^k),\\&-L_c^{k,N}(\varvec{\mathcal {C}}^{k,N}-\hat{\varvec{\mathcal {C}}}^{k,N})- \nabla _{\varvec{\mathcal {C}}}\ell (\hat{\varvec{\mathcal {C}}}^{k,N}, \mathbf {A}_{j<N}^k,{\mathbf {A}}_N^{k-1})+\nabla _{\varvec{\mathcal {C}}} \ell (\varvec{\mathcal {W}}^k)\\&\quad \in \partial r_c(\varvec{\mathcal {C}}^{k,N}) +\nabla _{\varvec{\mathcal {C}}}\ell (\varvec{\mathcal {W}}^k). \end{aligned}$$

Hence, for all $k\le K$,

$$\begin{aligned}&\text {dist}\big (\mathbf {0},\partial H(\varvec{\mathcal {W}}^k)\big )\nonumber \\&\quad \le \big \Vert (L_1^k(\mathbf {A}_1^k-\hat{\mathbf {A}}_1^k),\ldots ,L_1^k(\mathbf {A}_1^k- \hat{\mathbf {A}}_1^k),L_c^{k,n}(\varvec{\mathcal {C}}^{k,N}-\hat{\varvec{\mathcal {C}}}^{k,N}))\big \Vert _F \nonumber \\&\qquad +\sum _{n=1}^N\big \Vert \nabla _{\mathbf {A}_n}\ell (\varvec{\mathcal {C}}^{k,n}, \mathbf {A}_{j<n}^k,\hat{\mathbf {A}}_n^k,\mathbf {A}_{j\ge n}^{k-1})-\nabla _{\mathbf {A}_n}\ell (\varvec{\mathcal {W}}^k)\big \Vert _F\nonumber \\&\qquad +\big \Vert \nabla _{\varvec{\mathcal {C}}}\ell (\hat{\varvec{\mathcal {C}}}^{k,N}, \mathbf {A}_{j<N}^k,{\mathbf {A}}_N^{k-1})-\nabla _{\varvec{\mathcal {C}}}\ell (\varvec{\mathcal {W}}^k) \big \Vert _F\nonumber \\&\quad \le L_u\big (\Vert \mathbf {A}^k-\mathbf {A}^{k-1}\Vert _F+\Vert \mathbf {A}^{k-1}- \mathbf {A}^{k-2}\Vert _F\big )+L_u\big (\Vert \varvec{\mathcal {C}}^{k,N}- \varvec{\mathcal {C}}^{k,N-1}\Vert _F+\Vert \varvec{\mathcal {C}}^{k,N-1}-\varvec{\mathcal {C}}^{k,N-2}\Vert _F\big ) \nonumber \\&\qquad +\sum _{n=1}^NL_G\big (\Vert \varvec{\mathcal {C}}^{k,n}- \varvec{\mathcal {C}}^{k,N}\Vert _F+\Vert \mathbf {A}^k-\mathbf {A}^{k-1}\Vert _F+\Vert \mathbf {A}^{k-1}- \mathbf {A}^{k-2}\Vert _F\big )\nonumber \\&\qquad +L_G\big (\Vert \varvec{\mathcal {C}}^{k,N}-\varvec{\mathcal {C}}^{k,N-1}\Vert _F+\Vert \varvec{\mathcal {C}}^{k,N-1}- \varvec{\mathcal {C}}^{k,N-2}\Vert _F+\Vert \mathbf {A}^k-\mathbf {A}^{k-1}\Vert _F\big )\nonumber \\&\quad \le \big (L_u+(N+1)L_G\big )\left( \Vert \mathbf {A}^k-\mathbf {A}^{k-1}\Vert _F+\Vert \mathbf {A}^{k-1}- \mathbf {A}^{k-2}\Vert _F\right. \nonumber \\&\qquad \left. +\Vert \varvec{\mathcal {C}}^{k,N}-\varvec{\mathcal {C}}^{k,N-1}\Vert _F+ \sum _{n=1}^{N-1}\Vert \varvec{\mathcal {C}}^{k,n-1}-\varvec{\mathcal {C}}^{k,n}\Vert _F\right) , \end{aligned}$$

(57)

where we have used $L_n^k,L_c^{k,n}\le L_u,~\forall k, n$ and (52) to have the second inequality, and the third inequality is obtained from $\Vert \varvec{\mathcal {C}}^{k,n}-\varvec{\mathcal {C}}^{k,N}\Vert _F\le \sum _{i=n}^{N-1}\Vert \varvec{\mathcal {C}}^{k,i}-\varvec{\mathcal {C}}^{k,i+1}\Vert _F$ and doing some simplification. Using the KL inequality (54) at $\varvec{\mathcal {W}}=\varvec{\mathcal {W}}^k$ and the inequality

$$\begin{aligned} \frac{s^\theta }{1-\theta }(s^{1-\theta }-t^{1-\theta })\ge s-t,~\forall s,t\ge 0, \end{aligned}$$

we get

$$\begin{aligned} \frac{\gamma }{1-\theta }\text {dist}(\mathbf {0},\partial H(\varvec{\mathcal {W}}^k))(H_k^{1-\theta }-H_{k+1}^{1-\theta })\ge H_k-H_{k+1}. \end{aligned}$$

(58)

By (46), we have

$$\begin{aligned} H_k-H_{k+1} \ge&\frac{L_c^{k+1,N}}{2}\Vert \varvec{\mathcal {C}}^{k+1,N-1}-\varvec{\mathcal {C}}^{k+1,N}\Vert _F^2- \frac{L_c^{k,N}}{2}\delta _\omega ^2\Vert \varvec{\mathcal {C}}^{k,N-1}- \varvec{\mathcal {C}}^{k,N}\Vert _F^2\nonumber \\&+\sum _{n=1}^{N-1}\frac{(1-\delta _\omega ^2)L_c^{k+1,n}}{2}\Vert \varvec{\mathcal {C}}^{k+1,n-1}-\varvec{\mathcal {C}}^{k+1,n}\Vert _F^2\nonumber \\&+\sum _{n=1}^N\left( \frac{L_n^{k+1}}{2}\Vert \mathbf {A}_n^{k}- \mathbf {A}_n^{k+1}\Vert _F^2-\frac{L_n^{k}}{2}\delta _\omega ^2\Vert \mathbf {A}_n^{k-1}- \mathbf {A}_n^{k}\Vert _F^2\right) . \end{aligned}$$

(59)

Combining (57), (58), (59) and noting $L_c^{k+1,n}\ge L_d$ yield

$$\begin{aligned}&\frac{\gamma (L_u+(N+1)L_G)}{1-\theta }(H_k^{1-\theta }- H_{k+1}^{1-\theta })\big [\Vert \mathbf {A}^k-\mathbf {A}^{k-1}\Vert _F+\Vert \mathbf {A}^{k-1}- \mathbf {A}^{k-2}\Vert _F\nonumber \\&\quad \quad +\Vert \varvec{\mathcal {C}}^{k,N}-\varvec{\mathcal {C}}^{k,N-1}\Vert _F+\sum _{n=1}^{N-1}\Vert \varvec{\mathcal {C}}^{k,n-1}-\varvec{\mathcal {C}}^{k,n}\Vert _F\big ]\nonumber \\&\quad \quad +\delta _\omega ^2\left\| \left( \sqrt{L_1^k}\mathbf {A}_1^{k-1},\ldots , \sqrt{L_N^k}\mathbf {A}_N^{k-1},\sqrt{L_c^{k,N}}\varvec{\mathcal {C}}^{k,N-1} \right) \right. \nonumber \\&\quad \quad \left. -\left( \sqrt{L_1^k}\mathbf {A}_1^{k},\ldots , \sqrt{L_N^k}\mathbf {A}_N^{k},\sqrt{L_c^{k,N}} \varvec{\mathcal {C}}^{k,N}\right) \right\| _F^2\nonumber \\&\quad \ge \left\| \left( \sqrt{L_1^{k+1}}\mathbf {A}_1^{k},\ldots , \sqrt{L_N^{k+1}}\mathbf {A}_N^{k},\sqrt{L_c^{k+1,N}}\varvec{\mathcal {C}}^{k+1,N-1}\right) \right. \nonumber \\&\quad \quad \left. -\left( \sqrt{L_1^{k+1}}\mathbf {A}_1^{k+1},\ldots , \sqrt{L_N^{k+1}}\mathbf {A}_N^{k+1},\sqrt{L_c^{k+1,N}}\varvec{\mathcal {C}}^{k+1,N}\right) \right\| _F^2\nonumber \\&\quad \quad +\frac{(1-\delta _\omega ^2)L_d}{2}\sum _{n=1}^{N-1}\Vert \varvec{\mathcal {C}}^{k+1,n-1}- \varvec{\mathcal {C}}^{k+1,n}\Vert _F^2. \end{aligned}$$

(60)

By Cauchy-Schwart inequality, we estimate

$$\begin{aligned}&\sqrt{\text {right side of inequality (60)}}\nonumber \\&\quad \ge \frac{1+\delta _\omega }{2}\left\| \left( \sqrt{L_1^{k+1}}\mathbf {A}_1^{k}, \ldots ,\sqrt{L_N^{k+1}}\mathbf {A}_N^{k},\sqrt{L_c^{k+1,N}} \varvec{\mathcal {C}}^{k+1,N-1}\right) \right. \nonumber \\&\quad \quad \left. -\left( \sqrt{L_1^{k+1}}\mathbf {A}_1^{k+1},\ldots ,\sqrt{L_N^{k+1}} \mathbf {A}_N^{k+1},\sqrt{L_c^{k+1,N}}\varvec{\mathcal {C}}^{k+1,N}\right) \right\| _F\nonumber \\&\quad \quad +\eta \sum _{n=1}^{N-1}\Vert \varvec{\mathcal {C}}^{k+1,n-1}-\varvec{\mathcal {C}}^{k+1,n}\Vert _F, \end{aligned}$$

(61)

where $\eta >0$ is sufficiently small and depends on $\delta _\omega ,L_d,N$, and

$$\begin{aligned}&\sqrt{\text {left side of inequality (60)}}\nonumber \\&\quad \le \frac{\mu \gamma (L_u+(N+1)L_G)}{4(1-\theta )}(H_k^{1-\theta }-H_{k+1}^{1- \theta })\nonumber \\&\quad \quad +\frac{1}{\mu }\big [\Vert \mathbf {A}^k-\mathbf {A}^{k-1}\Vert _F+\Vert \mathbf {A}^{k-1}- \mathbf {A}^{k-2}\Vert _F+\Vert \varvec{\mathcal {C}}^{k,N}-\varvec{\mathcal {C}}^{k,N-1}\Vert _F\nonumber \\&\quad \quad +\sum _{n=1}^{N-1}\Vert \varvec{\mathcal {C}}^{k,n-1}- \varvec{\mathcal {C}}^{k,n}\Vert _F\big ]\nonumber \\&\quad \quad +\delta _\omega \left\| \left( \sqrt{L_1^k}\mathbf {A}_1^{k-1},\ldots , \sqrt{L_N^k}\mathbf {A}_N^{k-1},\sqrt{L_c^{k,N}}\varvec{\mathcal {C}}^{k,N-1} \right) \right. \nonumber \\&\quad \quad \left. -\left( \sqrt{L_1^k} \mathbf {A}_1^{k},\ldots ,\sqrt{L_N^k}\mathbf {A}_N^{k},\sqrt{L_c^{k,N}}\varvec{\mathcal {C}}^{k,N}\right) \right\| _F, \end{aligned}$$

(62)

where $\mu >0$ is a sufficiently large constant such that $\frac{1}{\mu }<\min (\eta ,\frac{1-\delta _\omega }{4}\sqrt{\frac{L_d}{2}}).$ Combining (60),(62), (61) and summing them over $k$ from 2 to $K$ give

$$\begin{aligned}&\frac{\mu \gamma (L_u+(N+1)L_G)}{4(1-\theta )}(H_2^{1-\theta } -H_{K+1}^{1-\theta })\\&\quad \quad +\frac{1}{\mu }\sum _{k=2}^K\big [\Vert \mathbf {A}^k-\mathbf {A}^{k-1}\Vert _F+\Vert \mathbf {A}^{k-1}-\mathbf {A}^{k-2}\Vert _F+\Vert \varvec{\mathcal {C}}^{k,N}- \varvec{\mathcal {C}}^{k,N-1}\Vert _F\\&\quad \quad +\sum _{n=1}^{N-1}\Vert \varvec{\mathcal {C}}^{k,n-1} -\varvec{\mathcal {C}}^{k,n}\Vert _F\big ]\\&\quad \quad +\delta _\omega \sum _{k=2}^K\left\| \left( \sqrt{L_1^k} \mathbf {A}_1^{k-1},\ldots ,\sqrt{L_N^k}\mathbf {A}_N^{k-1},\sqrt{L_c^{k,N}} \varvec{\mathcal {C}}^{k,N-1}\right) \right. \\&\quad \quad \left. -\left( \sqrt{L_1^k}\mathbf {A}_1^{k},\ldots ,\sqrt{L_N^k} \mathbf {A}_N^{k},\sqrt{L_c^{k,N}}\varvec{\mathcal {C}}^{k,N}\right) \right\| _F \\&\quad \ge \frac{1+\delta _\omega }{2}\sum _{k=2}^K\left\| \left( \sqrt{L_1^{k+1}}\mathbf {A}_1^{k},\ldots ,\sqrt{L_N^{k+1}} \mathbf {A}_N^{k},\sqrt{L_c^{k+1,N}}\varvec{\mathcal {C}}^{k+1,N-1}\right) \right. \\&\quad \quad \left. -\left( \sqrt{L_1^{k+1}}\mathbf {A}_1^{k+1},\ldots ,\sqrt{L_N^{k+1}} \mathbf {A}_N^{k+1},\sqrt{L_c^{k+1,N}}\varvec{\mathcal {C}}^{k+1,N}\right) \right\| _F\\&\quad \quad +\eta \sum _{k=2}^K\sum _{n=1}^{N-1}\Vert \varvec{\mathcal {C}}^{k+1,n-1}- \varvec{\mathcal {C}}^{k+1,n}\Vert _F. \end{aligned}$$

Simplifying the above inequality, we have

$$\begin{aligned}&\frac{\mu \gamma (L_u+(N+1)L_G)}{4(1-\theta )}(H_2^{1-\theta } -H_{K+1}^{1-\theta })\nonumber \\&\quad \quad +\frac{1}{\mu }\sum _{k=2}^K\left( \Vert \mathbf {A}^k-\mathbf {A}^{k-1}\Vert _F+\Vert \mathbf {A}^{k-1}- \mathbf {A}^{k-2}\Vert _F+\Vert \varvec{\mathcal {C}}^{k,N}-\varvec{\mathcal {C}}^{k,N-1}\Vert _F\right) \nonumber \\&\quad \quad +\delta _\omega \big \Vert \left( \sqrt{L_1^2}\mathbf {A}_1^{1},\ldots ,\sqrt{L_N^2} \mathbf {A}_N^{1},\sqrt{L_c^{2,N}}\varvec{\mathcal {C}}^{2,N-1}\right) \nonumber \\&\quad \quad -\left( \sqrt{L_1^2}\mathbf {A}_1^{2},\ldots ,\sqrt{L_N^2}\mathbf {A}_N^{2}, \sqrt{L_c^{2,N}}\varvec{\mathcal {C}}^{2,N}\right) \big \Vert _F\nonumber \\&\quad \ge \frac{1+\delta _\omega }{2}\left\| \left( \sqrt{L_1^{K+1}}\mathbf {A}_1^{K}, \ldots ,\sqrt{L_N^{K+1}}\mathbf {A}_N^{K},\sqrt{L_c^{K+1,N}}\varvec{\mathcal {C}}^{K+1,N-1} \right) \right. \nonumber \\&\quad \quad \left. -\left( \sqrt{L_1^{K+1}}\mathbf {A}_1^{K+1},\ldots ,\sqrt{L_N^{K+1}} \mathbf {A}_N^{K+1},\sqrt{L_c^{K+1,N}}\varvec{\mathcal {C}}^{K+1,N}\right) \right\| _F\nonumber \\&\quad \quad +\frac{1-\delta _\omega }{2}\sum _{k=2}^{K-1}\left\| \left( \sqrt{L_1^{k+1}}\mathbf {A}_1^{k},\ldots ,\sqrt{L_N^{k+1}}\mathbf {A}_N^{k}, \sqrt{L_c^{k+1,N}}\varvec{\mathcal {C}}^{k+1,N-1}\right) \right. \nonumber \\&\quad \quad \left. -\left( \sqrt{L_1^{k+1}}\mathbf {A}_1^{k+1},\ldots ,\sqrt{L_N^{k+1}} \mathbf {A}_N^{k+1},\sqrt{L_c^{k+1,N}}\varvec{\mathcal {C}}^{k+1,N}\right) \right\| _F\nonumber \\&\quad \quad +(\eta -\frac{1}{\mu })\sum _{k=2}^K\sum _{n=1}^{N-1}\Vert \varvec{\mathcal {C}}^{k+1,n-1}- \varvec{\mathcal {C}}^{k+1,n}\Vert _F. \end{aligned}$$

(63)

Note that

$$\begin{aligned}&\left\| \left( \sqrt{L_1^{k+1}}\mathbf {A}_1^{k},\ldots ,\sqrt{L_N^{k+1}}\mathbf {A}_N^{k}, \sqrt{L_c^{k+1,N}}\varvec{\mathcal {C}}^{k+1,N-1}\right) \right. \nonumber \\&\quad \quad \left. -\left( \sqrt{L_1^{k+1}}\mathbf {A}_1^{k+1},\ldots , \sqrt{L_N^{k+1}}\mathbf {A}_N^{k+1},\sqrt{L_c^{k+1,N}}\varvec{\mathcal {C}}^{k+1,N}\right) \right\| _F^2\nonumber \\&\quad =\sum _{n=1}^NL_n^{k+1}\Vert \mathbf {A}_n^k-\mathbf {A}_n^{k+1}\Vert _F^2+L_c^{k+1,N}\Vert \varvec{\mathcal {C}}^{k+1,N-1}-\varvec{\mathcal {C}}^{k+1,N}\Vert _F^2\nonumber \\&\quad \ge L_d(\Vert \mathbf {A}^k-\mathbf {A}^{k+1}\Vert _F^2+\Vert \varvec{\mathcal {C}}^{k+1,N-1}- \varvec{\mathcal {C}}^{k+1,N}\Vert _F^2\nonumber \\&\quad \ge \frac{L_d}{2}\left( \Vert \mathbf {A}^k-\mathbf {A}^{k+1}\Vert _F+\Vert \varvec{\mathcal {C}}^{k+1,N-1}- \varvec{\mathcal {C}}^{k+1,N}\Vert _F\right) ^2 \end{aligned}$$

(64)

Plugging (64) to inequality (63) gives

$$\begin{aligned}&\frac{\mu \gamma (L_u+(N+1)L_G)}{4(1-\theta )}\left( H_2^{1-\theta } -H_{K+1}^{1-\theta }\right) \\&\quad \quad +\frac{1}{\mu }\sum _{k=2}^K\left( \Vert \mathbf {A}^k-\mathbf {A}^{k-1}\Vert _F+\Vert \mathbf {A}^{k-1}-\mathbf {A}^{k-2}\Vert _F+\Vert \varvec{\mathcal {C}}^{k,N}-\varvec{\mathcal {C}}^{k,N-1}\Vert _F\right) \\&\quad \quad +\delta _\omega \Vert (\sqrt{L_1^2}\mathbf {A}_1^{1},\ldots , \sqrt{L_N^2}\mathbf {A}_N^{1},\sqrt{L_c^{2,N}}\varvec{\mathcal {C}}^{2,N-1})\\&\quad \quad -\left( \sqrt{L_1^2}\mathbf {A}_1^{2},\ldots ,\sqrt{L_N^2} \mathbf {A}_N^{2},\sqrt{L_c^{2,N}}\varvec{\mathcal {C}}^{2,N}\right) \Vert _F\\&\quad \ge \frac{1+\delta _\omega }{2}\sqrt{\frac{L_d}{2}} \left( \Vert \mathbf {A}^K-\mathbf {A}^{K+1}\Vert _F+\Vert \varvec{\mathcal {C}}^{K+1,N-1}-\varvec{\mathcal {C}}^{K+1,N}\Vert _F \right) \\&\quad \quad +\frac{1-\delta _\omega }{2}\sqrt{\frac{L_d}{2}} \sum _{k=2}^{K-1}\left( \Vert \mathbf {A}^k-\mathbf {A}^{k+1}\Vert _F+\Vert \varvec{\mathcal {C}}^{k+1,N-1}- \varvec{\mathcal {C}}^{k+1,N}\Vert _F\right) \\&\quad \quad +\left( \eta -\frac{1}{\mu }\right) \sum _{k=2}^K\sum _{n=1}^{N-1}\Vert \varvec{\mathcal {C}}^{k+1,n-1}-\varvec{\mathcal {C}}^{k+1,n}\Vert _F, \end{aligned}$$

which implies by noting $H_0\ge H_k\ge 0$, $\varvec{\mathcal {C}}^{k+1,0}=\varvec{\mathcal {C}}^{k,N}$ and $L_n^k,L_c^{k,n}\le L_u,~\forall k,n$ that

$$\begin{aligned}&\frac{\mu \gamma (L_u+(N+1)L_G)}{4(1-\theta )}H_0^{1-\theta }\nonumber \\&\qquad + \frac{1}{\mu }\left( 2\Vert \mathbf {A}^1-\mathbf {A}^{2}\Vert _F+\Vert \mathbf {A}^{0}- \mathbf {A}^{1}\Vert _F+\Vert \varvec{\mathcal {C}}^{2,N}-\varvec{\mathcal {C}}^{2,N-1}\Vert _F\right) \nonumber \\&\quad \quad +\delta _\omega \sqrt{L_u}\big (\Vert \mathbf {A}^1-\mathbf {A}^2\Vert _F+\Vert \varvec{\mathcal {C}}^{2,N-1}-\varvec{\mathcal {C}}^{2,N}\Vert _F\big )\nonumber \\&\quad \ge \frac{1+\delta _\omega }{2}\sqrt{\frac{L_d}{2}} \big (\Vert \mathbf {A}^K-\mathbf {A}^{K+1}\Vert _F+\Vert \varvec{\mathcal {C}}^{K+1,N-1}-\varvec{\mathcal {C}}^{K+1,N}\Vert _F \big )\nonumber \\&\quad \quad +\left( \frac{1-\delta _\omega }{2}\sqrt{\frac{L_d}{2}} -\frac{2}{\mu }\right) \sum _{k=2}^{K-1}\big (\Vert \mathbf {A}^k-\mathbf {A}^{k+1}\Vert _F+\Vert \varvec{\mathcal {C}}^{k+1,N-1}-\varvec{\mathcal {C}}^{k+1,N}\Vert _F\big )\nonumber \\&\quad \quad +\left( \eta -\frac{1}{\mu }\right) \sum _{k=2}^K\Vert \varvec{\mathcal {C}}^{k,N} -\varvec{\mathcal {C}}^{k+1,N-1}\Vert _F,\nonumber \\&\quad \ge \tau \big (\Vert \mathbf {A}^K-\mathbf {A}^{K+1}\Vert _F+\Vert \varvec{\mathcal {C}}^{K,N} -\varvec{\mathcal {C}}^{K+1,N}\Vert _F\big )\nonumber \\&\quad \quad +\tau \sum _{k=2}^{K-1}\big (\Vert \mathbf {A}^k-\mathbf {A}^{k+1}\Vert _F +\Vert \varvec{\mathcal {C}}^{k,N}-\varvec{\mathcal {C}}^{k+1,N}\Vert _F\big ), \end{aligned}$$

(65)

where $\tau =\min \left( \frac{1-\delta _\omega }{2}\sqrt{\frac{L_d}{2}}- \frac{2}{\mu },~\eta -\frac{1}{\mu }\right) .$ Let

$$\begin{aligned} T=\max \left( \frac{\mu \gamma (L_u+(N+1)L_G)}{4\tau (1-\theta )},~ \frac{1}{2\mu \tau }+\frac{\delta _\omega }{\tau }\sqrt{L_u}\right) . \end{aligned}$$

(66)

Then (65) implies

$$\begin{aligned}&T\big (H_0^{1-\theta }+\Vert \mathbf {A}^0-\mathbf {A}^1\Vert _F+\Vert \mathbf {A}^1-\mathbf {A}^2\Vert _F+\Vert \varvec{\mathcal {C}}^{2,N-1}-\varvec{\mathcal {C}}^{2,N}\Vert _F\big )\nonumber \\&\quad \ge \Vert \varvec{\mathcal {W}}^K-\varvec{\mathcal {W}}^{K+1}\Vert _F+\sum _{k=2}^{K-1}\Vert \varvec{\mathcal {W}}^k- \varvec{\mathcal {W}}^{k+1}\Vert _F , \end{aligned}$$

(67)

from which we have

$$\begin{aligned}&\Vert \varvec{\mathcal {W}}^{K+1}-\bar{\varvec{\mathcal {W}}}\Vert _F\\&\quad \le \Vert \varvec{\mathcal {W}}^K-\varvec{\mathcal {W}}^{K+1}\Vert _F+\sum _{k=2}^{K-1}\Vert \varvec{\mathcal {W}}^k- \varvec{\mathcal {W}}^{k+1}\Vert _F+\Vert \varvec{\mathcal {W}}^{2}-\bar{\varvec{\mathcal {W}}}\Vert _F\\&\quad \le T\big (H_0^{1-\theta }+\Vert \mathbf {A}^0-\mathbf {A}^1\Vert _F+\Vert \mathbf {A}^1-\mathbf {A}^2\Vert _F+\Vert \varvec{\mathcal {C}}^{2,N-1}-\varvec{\mathcal {C}}^{2,N}\Vert _F\big )\\&\quad +\Vert \varvec{\mathcal {W}}^{2}- \bar{\varvec{\mathcal {W}}}\Vert _F<\rho . \end{aligned}$$

Hence, $\varvec{\mathcal {W}}^{K+1}\in B(\bar{\varvec{\mathcal {W}}},\rho )$. By induction, we have $\varvec{\mathcal {W}}^{k}\in B(\bar{\varvec{\mathcal {W}}},\rho )$ for all $k$, so (67) holds for all $K$. Letting $K\rightarrow \infty$ gives $\sum _{k=2}^{\infty }\Vert \varvec{\mathcal {W}}^k-\varvec{\mathcal {W}}^{k+1}\Vert _F<\infty$, namely, $\{\varvec{\mathcal {W}}^k\}$ is a Cauchy sequence and, thus $\varvec{\mathcal {W}}^k$ converges. Since $\bar{\varvec{\mathcal {W}}}$ is a limit point of $\{\varvec{\mathcal {W}}^k\}$, then $\varvec{\mathcal {W}}^k\rightarrow \bar{\varvec{\mathcal {W}}}$. This completes the proof.