Skip to main content
SpringerLink
Log in

Temporal variation in deterministic chaos: the influence of Kainji dam on downstream stations along lower Niger River

  • Original Paper
  • Published:
Arabian Journal of Geosciences Aims and scope Submit manuscript

Abstract

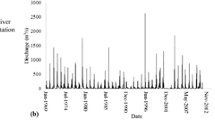
Complex systems such as river flow do not obey the law of linearity but most often than not behave in a nonlinear manner. In this study, the dynamics of the River Niger discharge along two stations located in Nigeria were investigated using the methods of phase space reconstruction, correlation dimension and Lyapunov exponent. The analysis was carried out by using the daily data for three different periods — 1914–1939 (period 1), 1940–1964 (period 2), and 1966–1991 (period 3) spanning before and after the Kainji dam construction. Time delay embedding values at Baro and Lokoja for the three time periods were used to reconstruct the phase space of the river discharge at both locations. The embedding dimension represents the number of variables to completely describe the system. The presence of chaos was confirmed with positive values of Lyapunov exponents in both locations at the three different periods considered. The Lyapunov exponents at Baro were in the range 0.0014–0.0150 while the range at Lokoja was 0.007–0.0145. Significant correlation dimension values obtained at Baro (2.11–2.81) and Lokoja (2.28–4.51) are indicative of low dimensional chaos. A possible explanation for this could be the temporal sequence in the dam installation. The forecast horizon, the inverse of the largest Lyapunov exponents, gives a prediction boundary on a chaotic time series. In this study, the forecast horizon for both locations is expected to be in the range of 40–58 days into the future.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  • Adamson PT, Rutherfurd ID, Peel MC, Conlan IA (2009) The hydrology of the mekong river. In: The Mekong. Elsevier, pp 53–76

  • Adelekan IO (1998) Spatio-temporal variations in thunderstorm rainfall over Nigeria. Int J Climatol: J R Meteorol Soc 18(11):1273–1284

    Article  Google Scholar 

  • Adeyemi O, Fashae OA (2018) Urbanisation and hydraulic geometry response: a model approach. Int J Water 12(2):103–115

    Article  Google Scholar 

  • Alami M, Ghorbani M, Malekani L (2013) Chaotic analysis and prediction of river flows. J Hydraul Struct 1(1):54–64

    Google Scholar 

  • Alfaro M, Fuertes G, Vargas M, Sepúlveda J, Veloso-Poblete M (2018) Forecast of chaotic series in a horizon superior to the inverse of the maximum Lyapunov exponent. Complexity, 2018

  • Alimohammadi H, Dastjerdi KY, Yaghin ML (2019) The study of progressive collapse in dual systems. Eng Arch 16(1):1–10

    Google Scholar 

  • Babovic V, Keijzer M (2000) Forecasting of river discharges in the presence of chaos and noise. In: Flood issues in contemporary water management. Springer, pp 405–419

  • Beauvais A, Dubois J (1995) Attractor properties of a river discharge dynamical system. Eos Transations AGU 73(46):F234

    Google Scholar 

  • Boon MY, Henry BI, Suttle CM, Dain SJ (2008) The correlation dimension: a useful objective measure of the transient visual evoked potential? J Vis 8(1):6–6

    Article  Google Scholar 

  • Fashae O, Olusola A, Adedeji O (2017) Geospatial analysis of changes in vegetation cover over Nigeria. Bull Geogr Phys Geogr Ser 13(1):17–27

    Article  Google Scholar 

  • Fashae O, Olusola A, Faniran A (2018) Environmental factors and pattern of riparian vegetation along the downstream sections of the Lower Ogun River, Nigeria. Singap J Trop Geogr 39(2):215–223

    Article  Google Scholar 

  • Fraedrich K (1986) Estimating the dimensions of weather and climate attractors. J Atmos Sci 43(5):419–432

    Article  Google Scholar 

  • Fraser AM, Swinney HL (1986) Independent coordinates for strange attractors from mutual information. Phys Rev A 33(2):1134

    Article  Google Scholar 

  • Fuwape IA, Ogunjo ST (2013) Investigating chaos in the Nigerian asset and resource management (arm) discovery fund. CBN J Appl Stat 4(2):129–140

    Google Scholar 

  • Fuwape IA, Ogunjo ST, Oluyamo S, Rabiu A (2017) Spatial variation of deterministic chaos in mean daily temperature and rainfall over Nigeria. Theor Appl Climatol 130(1):119–132

    Article  Google Scholar 

  • Ghorbani MA, Kisi O, Aalinezhad M (2010) A probe into the chaotic nature of daily streamflow time series by correlation dimension and largest Lyapunov methods. Appl Math Model 34(12):4050–4057. https://doi.org/10.1016/j.apm.2010.03.036, http://www.sciencedirect.com/science/article/pii/S0307904X10001575

    Article  Google Scholar 

  • Graf WL (2006) Downstream hydrologic and geomorphic effects of large dams on American rivers. Geomorphology 79(3-4):336– 360

    Article  Google Scholar 

  • Grassberger P, Procaccia I (1983) Characterization of strange attractors. Phys Rev Lett 50 (5):346

    Article  Google Scholar 

  • Hohensinner S, Hauer C, Muhar S (2018) River morphology, channelization, and habitat restoration. In: Riverine ecosystem management. Springer, Cham, pp 41–65

  • Jayawardena A, Lai F (1994) Analysis and prediction of chaos in rainfall and stream flow time series. J Hydrol 153(1-4):23–52

    Article  Google Scholar 

  • Kędra M (2014) Deterministic chaotic dynamics of Raba river flow (Polish carpathian mountains). J Hydrol 509:474–503

    Article  Google Scholar 

  • Kennel MB, Brown R, Abarbanel HD (1992) Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys Rev A 45(6):3403

    Article  Google Scholar 

  • Khatibi R, Sivakumar B, Ghorbani MA, Kisi O, Koa̧k K, Zadeh DF (2012) Investigating chaos in river stage and discharge time series. J Hydrol 414:108–117

    Article  Google Scholar 

  • Koutsoyiannis D (2006) On the quest for chaotic attractors in hydrological processes. Hydrol Sci J 51(6):1065–1091

    Article  Google Scholar 

  • Latrubesse EM, Stevaux JC, Sinha R (2005) Tropical rivers. Geomorphology 70(3-4):187–206

    Article  Google Scholar 

  • Leopold LB, Wolman MG, Miller JP (1995) Fluvial processes in geomorphology. Courier Corporation

  • Magilligan FJ, Nislow KH (2005) Changes in hydrologic regime by dams. Geomorphology 71 (1–2):61–78

    Article  Google Scholar 

  • Mallen-Cooper M, Zampatti BP (2018) History, hydrology and hydraulics: rethinking the ecological management of large rivers. Ecohydrology 11(5):e1965

    Article  Google Scholar 

  • Mihailovic DT, Nikolicoric E, Arsenic I, Malinovic Milicevic S, Singh VP, Stosic T, Stosic B (2019) Analysis of daily streamflow complexity by Kolmogorov measures and Lyapunov exponent. Physica A: Stat Mech Applic 525:290–303

    Article  Google Scholar 

  • Mitschke F, Dammig M (1993) Chaos versus noise in experimental data. Int J Bifur Chaos 3 (03):693–702

    Article  Google Scholar 

  • Ng W, Panu U, Lennox W (2007) Chaos based analytical techniques for daily extreme hydrological observations. J Hydrol 342(1–2):17–41

    Article  Google Scholar 

  • Ogunjo S, Fuwape I, Oluyamo S, Rabiu B (2019) Spatial dynamical complexity of precipitation and temperature extremes over Africa and South America. Asia-Pac J Atmos Sci, 1–14

  • Ogunjo S, Rabiu A, Fuwape I, Obafaye A (2021) Evolution of dynamical complexities in geospace as captured by dst over four solar cycles 1964–2008. J Geophys Res: Space Phys 126(4):e2020JA027873

    Article  Google Scholar 

  • Ogunjo ST, Fuwape IA (2020) Nonlinear characterization and interaction in teleconnection patterns. Adv Space Res 65(12):2723– 2732

    Article  Google Scholar 

  • Olusola A (2019) Process-form dynamics of upper Ogun river basin, southwestern Nigeria. Unpublished PhD thesis submitted to the department of geography University of Ibadan

  • Olusola AO, Fashae O (2017) Stream energy distribution below Eleyele dam in Southwestern Nigeria. Singap J Trop Geogr 38(3):402–413

    Article  Google Scholar 

  • Oyebande L (1995) Effects of reservoir operation on the hydrological regime and water availability in northern Nigeria. IAHS Publications-Series of Proceedings and Reports-Intern Assoc Hydrological Sciences 230 (1995):25–34

    Google Scholar 

  • Pasternack GB (1999) Does the river run wild? assessing chaos in hydrological systems. Adv Water Resour 23(3):253–260

    Article  Google Scholar 

  • Phillips JD (1992a) Deterministic chaos in surface runoff. Overland Flow: Hydraulic and Erosion Mechanics, pp 177–197

  • Phillips JD (1992b) Nonlinear dynamical systems in geomorphology: revolution or evolution? Geomorphology 5(3–5):219–229

    Article  Google Scholar 

  • Potter PE (1978) Significance and origin of big rivers. J Geol 86(1):13–33

    Article  Google Scholar 

  • Reiterer P, Lainscsek C, Schürrer F, Letellier C, Maquet J (1998) A nine-dimensional lorenz system to study high-dimensional chaos. J Phys A Math Gen 31(34):7121

    Article  Google Scholar 

  • Rosenstein MT, Collins JJ, De Luca CJ (1993) A practical method for calculating largest Lyapunov exponents from small data sets. Physica D: Nonlinear Phenomena 65(1-2):117–134

    Article  Google Scholar 

  • Savard C (1990) Correlation integral analysis of South Twin River streamflow, central nevada: preliminary application of chaos theory. Eos Transaction AGU 71(43):1341

    Google Scholar 

  • Schölzel C (2019) Nonlinear measures for dynamical systems. Zenodo 0.5.2, https://doi.org/10.5281/zenodo.3814723

  • Schreiber T (1993) Extremely simple nonlinear noise-reduction method. Phys Rev E 47(4):2401

    Article  Google Scholar 

  • Sivakumar B (2000) Chaos theory in hydrology: important issues and interpretations. J Hydrol 227(1–4):1–20

    Article  Google Scholar 

  • Sivakumar B (2016) Chaos in hydrology: bridging determinism and stochasticity. Springer

  • Sivakumar B (2017) Applications to river flow data. In: Chaos in hydrology. Springer, pp 267–295

  • Srivalli CN, Jothiprakash V, Sivakumar B (2019) Complexity of streamflows in the west-flowing rivers of India. Stoch Env Res Risk A 33(3):837–853

    Article  Google Scholar 

  • Stevaux JC, Martins DP, Meurer M (2009) Changes in a large regulated tropical river: The Paraná river downstream from the Porto Primavera dam, Brazil. Geomorphology 113(3-4):230–238

    Article  Google Scholar 

  • Stosic T, Telesca L, de Souza Ferreira DV, Stosic B (2016) Investigating anthropically induced effects in streamflow dynamics by using permutation entropy and statistical complexity analysis: a case study. J Hydrol 540:1136–1145

    Article  Google Scholar 

  • Takens F (1981) Detecting strange attractors in turbulence. In: Dynamical systems and turbulence, Warwick 1980. Springer, pp 366–381

  • Tongal H, Sivakumar B (2019) Entropy analysis for spatiotemporal variability of seasonal, low, and high streamflows. Stoch Environ Res Risk Assessment 33(1):303–320

    Article  Google Scholar 

  • Wang X, Lei T (2017) Hydrologic system behavior characteristic analysis and long-term prediction based on chaos radial basis function networks. Boletín Técnico 55(17):536–546

    Google Scholar 

  • Wohl EE (2007) Hydrology and discharge. Large rivers: Geomorphology and management, 29–44

  • Xiaofeng G, Lai CH (2000) Detecting chaos from time series. J Phys A: Math General 33 (5):1007–1016. https://doi.org/10.1088/0305-4470/33/5/313

    Article  Google Scholar 

  • Zadehmohamad M (2020) Evaluation of cyclic displacement amplitude of integral bridge abutment on backfill soil pressure and settlements. Journal of Transportation Research In press, 1–10

  • Zheng J, He H, Alimohammadi H (2021) Three-dimensional wadell roundness for particle angularity characterization of granular soils. Acta Geotech 16(1):133–149

    Article  Google Scholar 

  • Zhou Y, Ma Z, Wang L (2002) Chaotic dynamics of the flood series in the Huaihe River Basin for the last 500 years. J Hydrol 258(1–4):100–110

    Article  Google Scholar 

  • Zounemat-Kermani M (2016) Investigating chaos and nonlinear forecasting in short term and mid-term river discharge. Water Resour Manag 30(5):1851–1865

    Article  Google Scholar 

Download references

Author information

Author notes

  1. Adeyemi Olusola

    Present address: Department of Geography, University of the Free State, Bloemfontein, South Africa

  2. Ibiyinka Fuwape

    Present address: Michael and Cecilia Ibru University, Ughelli, Nigeria

Authors and Affiliations

  1. Department of Physics, Federal University of Technology, Akure, P. M. B. 704, Akure, Ondo State, Nigeria

    Samuel Ogunjo & Ibiyinka Fuwape

  2. Department of Geography, University of Ibadan, Ibadan, Oyo State, Nigeria

    Adeyemi Olusola

  3. Department of Geography, Osun State Univeristy, Osogobo, Osun State, Nigeria

    Olufemi Durowoju

Authors
  1. Samuel Ogunjo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Adeyemi Olusola
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ibiyinka Fuwape
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Olufemi Durowoju
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Samuel Ogunjo.

Ethics declarations

Conflict of interest

The authors declare no competing interests.

Additional information

Responsible Editor: Broder J. Merkel

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ogunjo, S., Olusola, A., Fuwape, I. et al. Temporal variation in deterministic chaos: the influence of Kainji dam on downstream stations along lower Niger River. Arab J Geosci 15, 237 (2022). https://doi.org/10.1007/s12517-021-09297-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12517-021-09297-0

Keywords

Search

Navigation