Skip to main content
SpringerLink
Log in

A mechanical model for the circular tunnel considering the interaction between the surrounding rock and support structure based on the unified strength criterion

  • Original Paper
  • Published:
Arabian Journal of Geosciences Aims and scope Submit manuscript

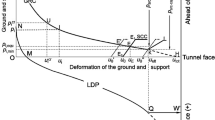
Abstract

It is very significant to study the stress and displacement fields in the surrounding rock induced by the tunnel excavation and its support. First of all, in order to take into account the effect of the intermediate principal stress on the tunnel surrounding rock mechanical behavior, the unified strength criterion (USC) is adopted to describe the plastic yield behavior of the surrounding rock. Secondly, the model proposed by Kastner does not consider the effect of the initial elastic displacement of the tunnel surrounding rock before the support structure is constructed and the interaction between the surrounding rock and the support structure. Therefore, a new mechanical model for the circular tunnel, which can overcome these shortcomings, is finally proposed by considering the tunnel practical construction process on basis of Kastner’s method. The effects of the calculation parameters such as the intermediate principal stress coefficient b, the initial elastic displacement u0 at the tunnel wall, the rock internal friction angle and the stiffness ks of the support structure on the surrounding rock plastic zone, and radial displacement of the tunnel wall are studied in detail. The results of the calculation examples show that the tunnel surrounding rock relative plastic zone rp/r0 and ground radial displacement us of the tunnel wall decrease with increasing b. With increasing u0, rp/r0 and us both increase, while with increasing ks and the rock internal friction angle, rp/r0 and us both decrease. In sum, it indicates that the proposed model for the circular tunnel can perfectly reflect the tunnel mechanical behavior.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  • Aftes (1983) Groupe de travail numerio 7-Recommendation sur l’emploi de la methode convergence-confnement. Dans Tunnels et ouvrages souterrains 59:218–238

    Google Scholar 

  • Bahrami B, Mohsenpour S, Miri MA, Mirhaseli R (2017) Quantitative comparison of fifteen rock failure criteria constrained by polyaxial test data. J Pet Sci Eng 159:564–580

    Article  Google Scholar 

  • Bian K, Liu J (2013) Analytical study of hydraulic tunnel in brittle rock masses with strain-softening characteristic. Disaster Adv 6(4):200–213

    Google Scholar 

  • Bobet A (2009) Elastic solution for deep tunnels: application to excavation damage zone and rockbolt support. Rock Mech Rock Eng 42(2):147–174

    Article  Google Scholar 

  • Brown ET, Bray JW, Ladanyi B, Hoek E (1983) Ground response curves for rock tunnels. J Geotech Eng 109:15–39

    Article  Google Scholar 

  • Cai Y, Jiang YJ, Ibrahim D, Tomomi I, Tetsuro E (2015) An analytical model considering interaction behavior of grouted rock bolts for convergence-confinement method in tunneling design. Int J Rock Mech Min Sci 76:112–126

    Article  Google Scholar 

  • Carranza-Torres C, Fairhurst C (2000) Application of the convergence-confinement method of tunnel design to rock masses that satisfy the Hoek–Brown failure criterion. Tunn Undergr Space Technol 15(2):187–213

    Article  Google Scholar 

  • Cheng YM (2012) Modified Kastner formula for cylindrical cavity contraction in Mohr-Coulomb medium for circular tunnel in isotropic medium. J Mech 28(1):163–169

    Article  Google Scholar 

  • Fan W, Yu MH, Deng LS, Peng XL, Chen LW (2013) New strength formulae for rock surrounding a circular opening. Can Geotech J 50(7):735–743

    Article  Google Scholar 

  • Fang Q, Zhang DL, Zhou P, Wong LNY (2013) Ground reaction curves for deep circular tunnels considering the effect of ground reinforcement. Int J Rock Mech Min Sci 60:401–412

    Article  Google Scholar 

  • Gonzalez-Nicieza C, Alvarez-Vigil AE, Menendez-Diaz A, Gonzalez-Palacio C (2008) Influence of the depth and shape of a tunnel in the application of the convergence-confinement method. Tunn Undergr Space Technol 23(1):25–37

    Article  Google Scholar 

  • Haruyama K, Teramoto S, Taira K (2005) Construction of large cross-section double-tier Metropolitan Inter-city Highway (Ken-O-Do) Ome Tunnel by NATM. Tunn Undergr Space Technol 20:111–119

    Article  Google Scholar 

  • Hou GY (2008) Review of interaction mechanism between surrounding rock and support and analysis of conceptual model of rheological deformation mechanism. Chin J Rock. Mech Eng 27((Supp.2)):3618–3629

    Google Scholar 

  • Huang F, Zhu HH, Li QS et al (2016) Field test and theoretical analysis of the loose zone of the surrounding rock of the tunnel. Rock Soil Mech 37(S1):145–150 (in Chinese)

    Google Scholar 

  • Jaeger JC, Cook NGW, Zimmerman RW (2007) Fundamentals of rock mechanics (Fourth Edition), Blackwell publishing

  • Jeffrey O, Nicholas V, Mark D (2018) Improvement to the convergence-confinement method: inclusion of support installation proximity and stiffness. Rock Mech Rock Eng 51:1495–1519

    Article  Google Scholar 

  • Jiang LZ, Chen J, Li J (2010) Seismic response of underground utility tunnels: shaking table testing and FEM analysis. Earthq Eng Eng Vib 9(4):555–567

    Article  Google Scholar 

  • Karakus M, Fowell RJ (2004) An insight into the New Austrian Tunnelling Method (NATM). Viith Regional Rock Mechanics Symposium, Sivas, Turkey, In

    Google Scholar 

  • Kastner H (1971) Static des Tunnel-und Stollenbaues. Springer, Berlin

    Book  Google Scholar 

  • Oettl G, Stark RF, Hofstetter G (1998) A comparison of elastic–plastic soil models for 2D FE analyses of tunneling. Comput Geotech 23(1-2):19–38

    Article  Google Scholar 

  • Oke J, Vlachopoulos N, Diederichs M (2018) Improvement to the convergence-confinement method: inclusion of support installation proximity and stiffness. Rock Mech Rock Eng 51:1495–1519

    Article  Google Scholar 

  • Oreste PP (2003a) A procedure for determining the reaction curve of the shotcrete lining considering transient conditions. Rock Mech Rock Eng 36(3):209–236

    Article  Google Scholar 

  • Oreste PP (2003b) Analysis of structural interaction in tunnels using the convergence-confinement approach. Tunn Undergr Space Technol 18:347–363

    Article  Google Scholar 

  • Oreste PP (2009) The convergence-confinement method: roles and limits in modern geomechanical tunnel design. Am J Appl Sci 6(4):757–771

    Article  Google Scholar 

  • Shin YJ, Song K, Lee IM, Cho GC (2011) Interaction between tunnel supports and ground convergence-consideration of seepage forces. Int J Rock Mech Min Sci 48:394–405

    Article  Google Scholar 

  • Sugimoto M, Chen J, Sramoon A (2019) Frame structure analysis model of tunnel lining using nonlinear ground reaction curve. Tunn Undergr Space Technol 94:103135

    Article  Google Scholar 

  • Wang Y (1996) Ground response of circular tunnels in poorly consolidated rock. J Geotech Eng-ASCE 122(9):703–708

    Article  Google Scholar 

  • Wang SL, Wu ZJ, Guo MW, Ge XR (2012) Theoretical solutions of a circular tunnel with the influence of axial in situ stress in elastic-brittle-plastic rock. Tunn Undergr Space Technol 30:155–168

    Article  Google Scholar 

  • Wang G, Liu CZ, Jiang YJ, Wu XZ, Wang SG (2015) Rheological model of DMFC rockbolt and rockmass in a circular tunnel. Rock Mech Rock Eng 48(6):2319–2357

    Article  Google Scholar 

  • Wang HN, Zeng GS, Utili S, Jiang MJ, Wu L (2017) Analytical solutions of stresses and displacements for deeply buried twin tunnels in viscoelastic rock. Int J Rock Mech Min Sci 93:13–29

    Article  Google Scholar 

  • Wu XZ, Jiang YJ, Guan ZC (2018) A modified strain-softening model with multi-post-peak behaviors and its application in circular tunnel. Eng Geol 240(5):21–33

    Article  Google Scholar 

  • Xiao Y, Zhao MH, Zhang R, Zhao H, Wu GQ (2019) Stability of dual square tunnels in rock masses subjected to surcharge loading. Tunn Undergr Space Technol 92:103037

    Article  Google Scholar 

  • Xu SQ, Yu MH (2006) The effect of the intermediate principal stress on the ground response of circular openings in rock mass. Rock Mech Rock Eng 39(2):169–181

    Article  Google Scholar 

  • Yu MH (2004) Unified strength criterion and its application. Springer, Berlin

    Book  Google Scholar 

  • Yu MH, Zan YW, Zhao J, Yoshimine M (2002) A unified strength criterion for rock material. Int J Rock Mech Min Sci 39:975–989

    Article  Google Scholar 

  • Yu DM, Fan YF, Duan JX, Luo XW (2013) Elastoplastic unified solutions to deep-buried circular tunnels considering intermediate principal stress. J Shanghai Jiao Tong Univ 47(9):1447–1453

    Google Scholar 

  • Zbigniew N, Piotr M, Tadeusz M (2018) Application of the NATM method in the road tunneling works in difficult geological conditions — the Carpathian flysch. Tunn Undergr Space Technol 74:41–59

    Article  Google Scholar 

  • Zhang M, Huang J, Ju NP, Zhang YL, Zhang GZ (2019) Inverse analysis on in-situ stress field of super-long and deep buried tunnel in Chuang-Zang railway. Chin J Undergr Space Technol 15(4):1049–1054 (in Chinese)

    Google Scholar 

  • Zhu YF, Zhang XS, Wang HP (2020) Analysis of complete process of interaction of surrounding rock and support under elastoplastic deformation condition. J Xi’an Univ Arch & Tech (Nat Sci Ed) 52(2):200–206 (in Chinese)

    Google Scholar 

  • Zou JF, Xia ZQ, Dan HC (2016) Theoretical solutions for displacement and stress of a circular opening reinforced by grouted rock bolt. Geomech Eng 11(3):439–455

    Article  Google Scholar 

Download references

Funding

This study is supported by “the National Key Research and Development Plan of China (Grant No:2019YFC1509701)”.

Author information

Authors and Affiliations

  1. School of Engineering and Technology, China University of Geosciences (Beijing), Beijing, 100083, China

    Hongyan Liu

  2. Key Laboratory of Deep Geodrilling Technology of Ministry of Natural Resources, Beijing, 100083, China

    Hongyan Liu

Authors
  1. Hongyan Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hongyan Liu.

Ethics declarations

Conflict of interest

The author declares no competing interests.

Additional information

Responsible Editor: Zeynal Abiddin Erguler

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, H. A mechanical model for the circular tunnel considering the interaction between the surrounding rock and support structure based on the unified strength criterion. Arab J Geosci 14, 753 (2021). https://doi.org/10.1007/s12517-021-07110-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12517-021-07110-6

Keywords

Search

Navigation