Introduction

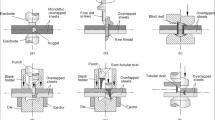
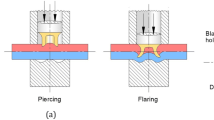
A reconfiguration of conventional self-pierce riveting (SPR) [1] is produced with Double-Sided Self-Pierce Riveting (DSSPR) [2] that, as its designation implies, is able to rivet both sheets simultaneously when placed in-between them by means of a tubular rivet with two chamfered ends. Then, the sheets are compressed against each other, and the ends of the tubular rivet are forced to pierce both sheets until a point where the strain-hardening levels developed in the sheet materials force the rivet to flare, thus producing a form-fit joint between both sheets. DSSPR is a mechanical joining by forming process [3] that employs an auxiliar joining element [4] (a tubular rivet) to produce a joint between two different geometries. This joining technology has shown its versatility by being able to join sheets made from both similar and dissimilar materials [5] to produce multi-material structures, similar to the capabilities of SPR [6] (Fig. 1).

Fig. 1
figure 1

Schematic representation of the process sequence at the start and end of the process to join thinner (left) and thicker (right) sheets by means of a self-pierce riveting and b double-sided self-pierce riveting

Full size image

Softer materials like PVC were previously joined to aluminium by DSSPR, through the utilization of different chamfered angles at each rivet end that are flatter or sharper to account for the easiness or difficult of joining each material, respectively, while guaranteeing a balanced amount of rivet material in each sheet. To that some purpose, other joining strategies included pre-riveting the harder material to create a rigid rivet-sheet system that will then be riveted to the softer material.

This innovative double-sided self-pierce riveting process (DSSPR) has some important highlights in comparison with self-pierce riveting (SPR), as the ability to join different and larger thicknesses without dedicated tools and without tearing up one or more sheets, with a tubular rivet that remains hidden inside the sheets and not exposed to the elements such as galvanic corrosion. At the same time, reduced to non-existent material protrusions are produced in the sheet surfaces. The size of these protrusions will depend on the amount of rivet volume that is pushed inside the sheets, since this effect can be followed by excessive outer material flow that can induce some defects in the geometries to be joined.

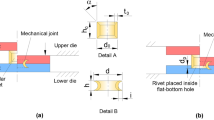
The original validation of the DSSPR joining technology [2] has been performed with tubular rivets of stainless steel AISI 304 with a constant external diameter \({d}_{0}\) of 10 mm and a constant thickness \({t}_{0}\) of 1.5 mm (refer to Fig. 2a and b). Variations were introduced to the initial rivet height \({h}_{0}\) and chamfered angle \(\alpha\). The importance of the chamfered angle design was already discussed in [7].

Fig. 2
figure 2

Schematics of the a initial and b deformed rivet cross-sections and of the original sheet

Full size image

Aluminium AA5754 sheets with a thickness \({t}_{s}\)of 5 mm and a length \(L\) and width \(w\) of 50 mm (Fig. 2c) were originally tested [2], since contrary to what it is observed for SPR, no upper thickness limit is observed for DSSPR. The conclusion was that the ideal solution was found for rivets with chamfered ends between 30 and 45° and initial heights between 8 and 10 mm, however a proper definition of the rivet parameters, mainly the relation between the chamfered angle of the rivet ends and the ratio between the initial height and thickness of the rivet is still needed to ensure an optimal compromise between weight, energy, cost and aesthetics.

In this paper, the correct parameter combination was established through a combination of numerical tools and experimentation, following a modified strategy of that utilized for SPR [8], to identify the requirements of force and energy, the corresponding performance of each joint to shear tests [9], as well as the dimension of the protuberance produced above the sheet surface. Then, an additional rivet was introduced to assess the improvements in the performance of the mechanical joint at a real scenario application.

To completely establish the ratio between the initial height and thickness of the rivet for these materials, different thinner and thicker sheet combinations were also analysed.

Methods and procedures

Material selection

The material selection and respective material curves were retrieved from the original work of conventional DSSPR [2] carried out by the authors. Although some modifications were introduced to the original tubular rivet, the material characterization started from AISI 304 stainless steel tubes with a 1.5 mm wall thickness and an outer diameter of 10 mm and commercial AA5754-H111 aluminum sheets with 5 mm-thickness. Those mechanical characterizations were performed in a hydraulic testing machine (Instron SATEC 1200 kN) with a cross-head speed of 10 mm/min by means of tensile and stack compression tests from which resulted the following flow curves approximated by means of a power-law hardening model (Ludwik-Holomon):

$$\begin{array}{c}\mathrm{Stainless}\;\mathrm{steel}\;\mathrm{AISI}\;304:\;\mathrm\sigma=1270.5\mathrm\epsilon^{0.44}\\ \mathrm{Aluminium}\;\mathrm{AA}5754-\mathrm H111:\;\sigma=329.3\epsilon^{0.23}\end{array}$$
(1)

This information will be utilized to develop the numerical predictions that explain the deformation mechanisms introduced by the modification of the main process variables in order to achieve the optimal height-thickness ratio for the tubular rivet.

Test variables

The main test variables can be summarized for the tubular rivet as its outer diameter \({d}_{0}\), wall thickness \({t}_{0}\), height \({h}_{0}\) and chamfered angles \(\alpha\) of its ends. From those parameters, only the outer diameter was kept constant along this research work. The experimentation was carried at room temperature conditions at the same hydraulic testing machine with the same cross-head speed as before.

As seen in Table 1, the workplan consists in finding the optimal initial thickness \({t}_{0}\) for each initial height \({h}_{0}\) for two different chamfered angles \(\alpha\). This will be achieved by a combination of finite element simulations with some of them being validated by experimental tests, that will then be subjected to shear destructive tests to identify which combination provides the best results.

Table 1 Test variables for the identification of the optimal parameter combination (refer to Fig. 1b)
Full size table

After the definition of the suitable chamfered angle \(\alpha\) and range of the ratio \({h}_{0}/{t}_{0}\)of the rivet, the DSSPR process was applied to thinner sheets with a thickness of 1.5 mm and its combination with the previous thicker sheets of 5 mm-thickness of the same material, according to Table 2.

Table 2 Test variables for the application of DSSPR to sheets of different thicknesses (refer to Fig. 1b)
Full size table

A minimum of five specimens were produced for each combination that were subjected not only to destructive testing, but also carefully analysed and halved lengthwise to conclude about the undercut \(i\) (refer to Fig. 1b) and take conclusions about their influence in the performance of the mechanical joint produced.

Numerical simulations

The finite element computer program i-form [10] was utilized to evaluate the influence of the different parameter combination. This software was already validated for previous works on DSSPR and also for different other joining by forming techniques. Its algorithm is built upon the quasi-static finite element flow formulation and takes in consideration the contact and sliding with friction between deformable objects.

The numerical modelling conditions are the following: the cross-sections of both the tubular rivets and sheets were discretized by quadrilateral elements and these geometries were modelled as deformable isotropic objects subjected to axisymmetric loading in rotational symmetry conditions, with the calculations being restricted to the first quadrant of their cross-sections; the tools had their contours discretized by linear friction elements and were modelled as rigid objects (Fig. 3).

Fig. 3
figure 3

Numerical model and respective experimental cross-section at the start and finish of the DSSPR joining process for a rivet with an initial height \({h}_{0}\) of 8 mm and an initial wall thickness \({t}_{0}\)of 1.25 mm

Full size image

Whenever large distortions were created in the meshes along the numerical simulations, that are the result of large local deformations produced by the penetration of the tubular rivet along the sheets thicknesses, local mesh repairment complemented by intermediate global remeshings of the entire deformed objects were performed with the software. This ensures a proper integrity of the field variables along the simulations.

The von Mises constitutive equations were employed for the finite element formulation and a rigid-plastic material model was utilized, with the material data being retrieved for each geometry from its respective power law equation presented in (1).

Friction was modelled according with a constant law of friction \(\tau =mk\), where the friction factor \(m\) took different values according to reference values for stainless steel and aluminium combinations. Those values are summarized in Table 3 and the validation of the friction conditions was obtained by the close correlation between the numerically predicted and experimental force-displacement evolutions.

Table 3 Values of the friction factor \(m\) according to the contact interface
Full size table

Results and discussion

Influence of the chamfered angle of the rivet ends

It was previously verified that larger undercuts resulting from larger flaring radius were triggered by smaller values of the chamfered angle \(\alpha\) of the original rivets [2]. These smaller angles resulted in a better clamping between the adjoining sheets while demanding slightly smaller force-energy levels at the beginning of piercing and flaring of the rivet through the sheets, until a point where the entire rivet wall thickness is almost in full contact with the sheets. At the same time, sharper angles can create some difficulties for the control and repeatability of the DSSPR process, since smaller variations at the sharp and slender rivet end can have a negative influence in the rivet deformation and give rise to significant variations of the undercut [5]. Thus, it becomes necessary to evaluate the gains in terms of performance that result from the utilization of chamfered angles of 30 and 45 degrees. For that purpose, tubular rivets with an initial wall thickness \({t}_{0}\)of 1.5 mm and an initial height \({h}_{0}\) of 10 mm are utilized. The reason for this choice of parameters in this comparison is due to the conclusions taken from the original work of DSSPR [2], in which it was observed that the undercut \(i\) increases with the increase in the initial height \({h}_{0}\) up to a height immediately below the critical height were plastic instability of the rivet is triggered.

As seen in Fig. 4, although the undercut \(i\) produced by the rivet with a chamfered angle of 30 degrees is slightly higher than for an angle of 45 degrees (1.20 mm vs. 0.89 mm, respectively), the peak force that the joint can withstand before the sheets start to get separated is considerably smaller. This can be justified by the morphology of the rivet geometry having a chamfered angle of 30 degrees, where the slender rivet ends facilitate the detachment of the sheet from the rivet during the destructive shear tests.

Fig. 4
figure 4

Results from the destructive shear tests of rivets with an initial wall thickness \({t}_{0}=1.5 \ mm\) and height \({h}_{0}=10 \ mm\) for two different chamfered angles \(\alpha\) of 30 and 45 degrees, with photographs of the respective experimental cross-sections

Full size image

Therefore, it can be concluded that the utilization of very sharp angles should be restricted to scenarios in which the resistance of the materials to be riveted is very close to that of the tubular rivet where the rivet penetration becomes more difficult, and even then, it is preferable to increase the resistance of the tubular rivet material.

Analysis of the rivet height-thickness ratio

The influence of the initial height \({h}_{0}\) for a constant wall thickness \({t}_{0}=1.5 \ mm\) was already addressed in the original work on DSSPR [2]. From that study, it was observed that when the initial heights are equal or larger than a critical limiting height \({h}_{0}=12 \ mm\), the tubular rivets tend to fail by plastic instability and are not able to pierce through the sheets. If the initial rivet height is smaller than that critical height, clamping is successfully achieved but if the initial height is much smaller (for the same initial rivet thickness \({t}_{0}\)), the rivet tends to only enlarge its wall thickness and the amount of flaring is very reduced. To identify the suitable values of initial rivet height \({h}_{0}\) it is necessary to understand that along the indentation, combined piercing and flaring until the clamping stage, the rivet wall thickness increases due to the compression and strain hardening of both the rivet and the sheets. The latter is responsible by promoting combined piercing and flaring of the rivet inside the sheets which produces the mechanical interlocking.

Although the undercut produced by an initial rivet height of 8 and 10 mm was almost the same for a wall thickness of 1.5 mm (0.87 and 0.89 mm, respectively), it is still necessary to verify if the same is observed for the shear resistance of the joints produced with those two rivet dimensions.

The results of Fig. 5 for the evolution of the riveting forces with displacement and for the destructive shear forces allow to take different conclusions. Regarding Fig. 5a, the increase of the initial height \({h}_{0}\) will increase the volume of rivet material being pushed inside the sheets, which in turn translates in an increase of the riveting force and energy necessary to complete the joining process. As the initial height \({h}_{0}\) increases, the rivet becomes more curled which results in a final rivet shape with a lower final height \(h\) and larger final diameter \(d\), and consequently, a larger undercut \(i\) (refer to the inserts of the graph of Fig. 5a). This will have an important effect on the performance of the mechanical joint to shear tests, where for the same initial rivet thickness \({t}_{0}\) of 1.5 mm, the larger initial rivet height of 10 mm is able to withstand a peak force that is almost 4 kN higher than for a rivet height of 8 mm as seen on Fig. 5b.

Fig. 5
figure 5

a Numerical and experimental force-displacement evolutions of the riveting force with displacement; b Destructive force-displacement evolutions for the shear tests on DSSPR joints with different initial rivet heights and thicknesses for the same chamfered angle of 45 degrees

Full size image

This is compatible with the conclusions from the original work on DSSPR [2] but leads to the question: can the riveting force and deformation be reduced while maintaining a similar performance for the mechanical joint? To answer this question, variations of the wall thickness \({t}_{0}\) were introduced to rivets having initial heights \({h}_{0}\) of 8 and 10 mm, in an effort to obtain the optimal ratio \({h}_{0}/{t}_{0}\) for these specific materials of both the sheets and rivet (refer to Fig. 6).

Fig. 6
figure 6

Experimental cross-sections with details of the protrusions produced above the sheet surface for a \({h}_{0}=10 \ mm\); \({t}_{0}=1.5 \ mm\); b \({h}_{0}=8 \ mm\); \({t}_{0}=1.5 \ mm\); c \({h}_{0}=8 \ mm\); \({t}_{0}=1.25 \ mm\)  

Full size image

Considering that an initial height of 10 mm along with a thickness of 1.5 mm and a chamfered angle of 45 degrees provides the best performance values, different initial thicknesses were numerically tested for the initial height of 8 mm while keeping a constant chamfered angle of 45 degrees, until a larger undercut than for the original conditions was observed. From this analysis, it was possible to conclude that a larger undercut is obtained for a thickness of 1.25 mm, that as shown in Fig. 4a is able to offer a lower riveting force and energy than an initial height of 10 mm, while increasing the peak value of the shear force in 2 kN in relation with a rivet thickness of 1.5 mm and initial height of 8 mm. The amount of outward material flow and the protrusions created above the sheet surfaces are now smaller than for the previous cases as shown in Fig. 6, where the respective experimental cross-sections of all tested cases are depicted.

From the previous results, it can be concluded that the optimal values for the ratio \({h}_{0}/{t}_{0}\) for the materials are within the range of 6.4 to 6.7. The choice for the upper or lower limit of this range will be determined by the requirements of destructive force and energy established during the design stage of the intended application.

Another interesting analysis is related to the application of the optimal ratio \({h}_{0}/{t}_{0}\) previously identified to a smaller initial rivet height. According to the established ratio, an initial height \({h}_{0}\) of 6 mm was numerically tested with a corresponding initial thickness \({t}_{0}\) of 0.9 mm that matches the interval of the optimal ratio \({h}_{0}/{t}_{0}\). It is worth mentioning that this height was originally found to result in an enlargement of the rivet wall thickness during the joining process which produced a small undercut [2].

From the results presented on Fig. 7, it is observed that the very slender rivet (Fig. 7a) has some difficulties in being able to penetrate the sheets and it starts to flare from the initial stages which forces the sheet material to flow outwardly in the radial direction, resulting in a weak mechanical joint. In turn, for the optimized rivet with an initial height \({h}_{0}\) of 8 mm and thickness \({t}_{0}\) of 1.25 mm (Fig. 7b), the sheet material flows along the direction of the penetration of the rivet end, which as previously seen in Fig. 6c, allows to produce a sound joint. Thus, it can be concluded that the optimal ratio \({h}_{0}/{t}_{0}\) can only be applied to values of the initial height \({h}_{0}\) outside the minimum and maximum critical height of the rivet material [2]. Although the thickness was changed, the values of these limits remain constant.

Fig. 7
figure 7

Finite element predictions of the normalized radial velocity \({v}_{\text{r}}/{v}_{0}\) for a \({h}_{0}=6 \ mm\); \({t}_{0}= 0.90 \ mm\) and b \({h}_{0}=8 \ mm\); \({t}_{0}=1.25 \ mm\)

Full size image

Assessment of the introduction of an additional rivet

Following the optimization of the rivet parameters for DSSPR of AA5754-H111 sheets by means of AISI304 rivets, it becomes necessary to analyse the influence of introducing more than one rivet to simulate a real application where more than one joint is produced along a given geometry. For that purpose, the spacing in between rivets and the edges of the sheets needs to be respected to avoid defects in the final assembly. This analysis was already done for aluminium AA5754 sheets for a Self-Pierce Riveting Process (SPR), which established the suitable values of spacing between rivets and distance from the edges of the sheets [11]. It was verified that a distance \(d\) between rivets of approximately 2.5 times the outer diameter of the rivet did not produce any defects and that a minimum edge distance \(w\) of 1.5 times the outer diameter of the rivet needs to be respected to achieve a good fatigue performance.

With these conclusions, two sets of joints were fabricated with sheets with a thickness \({t}_{\text{s}}\)of 5 mm and rivets with an initial height \({h}_{0}\) of 10 mm and an initial wall thickness \({t}_{0}\)of 1.5 mm, disposed along the horizontal and vertical directions to evaluate the performance of the DSSPR joint in each scenario. The schematics of the double joints are presented in Fig. 8a and the resulting joints are shown in Fig. 8b.

Fig. 8
figure 8

a Schematic of the two sets of joints having different rivet dispositions where \(d\) (25 mm) and \(w\) (37.5 mm) are the edge distances. b Respective photographs of the assembly after joining

Full size image

From the results of the destructive performance of the horizontal and vertical DSSPR joints, it is verified that the peak force values at which the tubular rivets start to separate from the sheets are very similar, with only a small difference in the maximum force of approximately 1.5 kN. This difference may be due to the bending effects verified during the shear tests (refer to the insert of Fig. 9a) that are better surpassed by the vertically disposed rivets which offer an additional resistance to that movement.

Fig. 9
figure 9

a Force-displacement evolution for the destructive shear tests on DSSPR joints with a single rivet and with two rivets disposed in different orientations with a photograph of the experimental setup. b Photographs of the double rivet joints after those destructive tests

Full size image

Comparing the results for the utilization of single and double rivets, one may expect that the utilization of an additional rivet could result in a maximum detachment force that was double than that of a single rivet joint. However, the detachment of the tubular rivet from the sheets results from the deformation of the sheet at the contact region with the rivet wall (refer to Fig. 9b), which becomes more difficult for higher values of undercut. This justifies the fact that with the introduction of an additional rivet, the overall level of deformation at the sheet and the overall force levels become higher, since the deformation is occurring simultaneously in two different locations where the rivet is in contact with the sheets. Therefore, it can be concluded that the maximum load that a DSSPR joint can withstand is limited by the resistance of the sheet. If the sheets are made from different materials, the performance will be limited by the sheet with the lower resistance as seen in [5].

Application to different sheet thicknesses

The application of DSSPR to join thinner and thicker sheets allows to extend the range of applications for the joining technology. These conditions present themselves as a limitation for the applicability of SPR which is generally limited to combinations of sheets with smaller thicknesses [12], since the upper sheet needs to be completely teared up during the joining process, while avoiding the occurrence of plastic instability at the semi-tubular rivet. The upper sheet also needs to be made from a softer material than the lower sheet. To prove the feasibility of DSSPR in those conditions, a smaller sheet thickness of 1.5 mm (which was previously joined with DSSPR by the authors [13]) was joined to a larger sheet thickness of 5 mm. Following the same principle utilized for the selection of the initial rivet height in the original work of DSSPR [2], an initial rivet height of 3 mm was selected that is double of the initial sheet thickness. According to the ratio \({h}_{0}/{t}_{0}\) previously identified, a thickness of approximately 0.5 mm must be chosen for a tubular rivet of that height. To produce joints between sheets with different thicknesses, the previous rivet parameters (\({h}_{0}=3 mm\) and \({t}_{0}=0.5 mm\)) can also be utilized if the thickness of the thinner sheet remains constant, since the smaller sheet thickness determines the choice of the rivet parameters. The numerical results for the combination between a sheet with 1.5 mm-thickness and a sheet with 5 mm-thickness are presented in Fig. 10.

Fig. 10
figure 10

Distribution of effective strain for two different sheet thicknesses of 1.5 and 5 mm, obtained with the same rivet parameters utilized for joining 1.5 mm-thickness sheets without a and with b a pre-riveting operation

Full size image

Looking at Fig. 10a, it can be seen that due to the reduced sheet thickness, the strain levels at the top of the thinner sheet near the rivet end become very high. This creates difficulties to the penetration of the rivet in that sheet, and in turn, the rivet tends to flare and enlarge its thickness. To circumvent this situation, in Fig. 10b, a pre-riveting operation [5] was previously applied to the thicker sheet to ensure a proper penetration of that sheet, and then in a subsequent operation, the thinner sheet is joined to the pre-riveted materials, which results in a better penetration and clamping of the DSSPR joint.

Conclusions

The working limits of the original work on DSSPR were carefully assessed from which it was firstly concluded, that although the undercut produced by the rivet with a chamfered angle of 30 degrees is slightly higher than for an angle of 45 degrees, the morphology of the slender rivet geometry with lower volume of rivet material at the ends facilitates the separation of the sheet from the rivet, and may also create some difficulties for the control and repeatability of the DSSPR process.

The choice of a suitable rivet thickness within the optimal height-thickness ratio identified along this research allows to employ tubular rivets of lower volume, which are able to reduce the protrusions produced above the sheet surfaces while maintaining a proportional performance level.

The introduction of an additional rivet to replicate a more real use of the DSSPR technology has shown to be able to increase the maximum destructive force independently of the rivets’ disposition, although the performance of the DSSPR joint is limited by the resistance of the softer sheet.

The range of the height-thickness ratio can be successfully applied to thinner sheets and to combinations between sheets of different thicknesses, where additional joining strategies may be necessary to produce a sound DSSPR joint. Overall, the single disadvantage of DSSPR in comparison with SPR is only found for very small sheet thicknesses lower than 1 mm, where the smaller tubular rivets necessary to produce the joint may create some constraints during their automated handling and positioning in-between the sheets.