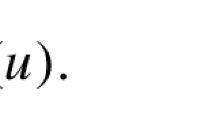A Note on the Evolution of the Whitney Sphere Along Mean Curvature Flow

Abstract

We study the evolution of the Whitney sphere along the Lagrangian mean curvature flow. We show that equivariant Lagrangian spheres in ${{\mathbb {C}}^n}$ satisfying mild geometric assumptions collapse to a point in finite time and the tangent flows converge to a Lagrangian plane with multiplicity two.

1 Introduction

The Whitney sphere is the immersion $F: {{\mathbb {S}}^n} \rightarrow {{\mathbb {R}}^{2n}}$ given by

$$\begin{aligned} F(x_1,\ldots ,x_{n+1})=\frac{1}{1+x_{n+1}^2}(x_1,x_1x_{n+1},\ldots ,x_n,x_nx_{n+1}). \end{aligned}$$

This immersion is Lagrangian, i.e., $F^{*}\omega =0$, where $\omega$ is the standard symplectic form on ${\mathbb {R}}^{2n}$. From the point of view of topology, the Whitney sphere is interesting since it has the best topological behavior: namely, it fails to be embedded only at the north and south pole where it has a transversal double point. An well known result of Gromov asserts that there are no embedded Lagrangian spheres in ${\mathbb {C}}^n$. On the geometry side, this immersion can be characterized by many geometric rigidity properties, see [3, 12]. In this sense, the Whitney sphere plays the role of totally umbilical hypersurfaces in ${\mathbb {R}}^n$ in the class of Lagrangian submanifolds.

Another interesting aspect of the Whitney sphere is that it appears as a limit surface under Lagrangian mean curvature flow of some well-behaved Lagrangian submanifolds in ${\mathbb {R}}^4$. Recall that the mean curvature flow (MCF) of an immersion $F_0: M^k\rightarrow {\mathbb {R}}^m$ is a map $F: M\rightarrow [0,T]\rightarrow {\mathbb {R}}^m$ such that $F(x,0)=F_0$ and satisfies the equation

$$\begin{aligned} \frac{\mathrm{{d}}}{\mathrm{{d}}t} F= H, \end{aligned}$$

where H is the mean curvature vector of $M^n$. It was shown by Smoczyk that the Lagrangian condition is preserved by MCF when the ambient space is a Kähler-Einstein manifold. The Lagrangian mean curvature flow gained a lot of interest recently as a potential tool to find minimal Lagrangian (special Lagrangian) in a given homology class or Hamiltonian isotopy class of a Calabi–Yau manifold. Special Lagrangian submanifolds have the remarkable property of being area minimizing by means of calibration arguments. The classical approach of minimizing area in a given class, however, does not seem very effective to find smooth special Lagrangian as shown by Schoen and Wolfson in [13].

Ideally, one could hope that the evolution of well behaved Lagrangian submanifolds along mean curvature flow to converge to special Lagrangians. In a series of works, A. Neves showed that finite time singularities are unavoidable in the Lagrangian mean curvature flow in general, see [8, 10]. It is constructed in [8] a non-compact zero Maslov class Lagrangian in ${{\mathbb {R}}^4}$ with bounded Lagrangian angle and in the same Hamiltonian isotopy class of a Lagrangian plane that nevertheless develops a singularity in finite time. At the singular time the limit surface pictures like a connect sum of a smooth Lagrangian (diffeomorphic to a Lagrangian plane) with a Whitney sphere. Such construction were later generalized to 4-dimensional Calabi–Yau manifolds, see [10].

There are very few results regarding the evolution of compact Lagrangian submanifolds in ${{\mathbb {C}}^n}$. Motivate by this, we investigate the evolution of the Whitney sphere along mean curvature flow. Despite its many geometric properties, it is not a self-similar solution of the flow. By exploiting its rotationally symmetries, one can reduce its mean curvature flow to a flow about curves in the plane. As a particular case of our main result we prove

Let $F: {{\mathbb {S}}^n}\times [0,T)\rightarrow {\mathbb {C}}^{n}$ be the maximal existence mean curvature flow of the Whitney sphere. Then $F_T(x)=\{0\}$ for every $x\in {{\mathbb {S}}^n}$. The tangent flow at the origin is a Lagrangian plane with multiplicity two.

A Lagrangian submanifold $L\subset {\mathbb {C}}^{n}$ is called equivariant if there exists a antipodal invariant curve $\gamma : I\rightarrow {\mathbb {C}}$ such that L can be written as

$$\begin{aligned} L=\{(\gamma (u)\, G_1(x),\ldots , \gamma (u)\, G_n(x))\in {{\mathbb {C}}^n}\,:\, G: {\mathbb {C}}^{n-1}\rightarrow {\mathbb {R}}^{n}\}, \end{aligned}$$

where G is a the standard embedding of ${\mathbb {C}}^{n-1}$ in ${\mathbb {R}}^n$. Using spherical coordinates on ${{\mathbb {C}}^n}$, $(\cos (u)\,G(x), \sin (u))$, we check that the Whitney sphere is equivariant with associated curve $\gamma _0: (0,2\pi )\rightarrow {\mathbb {R}}^2$ given by:

$$\begin{aligned} \gamma _0(u)=\bigg (\frac{\sin (u)}{1+\cos ^2(u)},\frac{\sin (u)\cos (u)}{1+\cos ^2(u)}\bigg ). \end{aligned}$$

The equivariant property is preserved by the mean curvature flow and the corresponding evolution equation for $\gamma _t$ is

$$\begin{aligned} \frac{\mathrm{{d}}\gamma }{\mathrm{{d}}t}=\overrightarrow{k}-(n-1)\, \frac{\gamma ^{\perp }}{|\gamma |^2}. \end{aligned}$$

(1.1)

Here$\overrightarrow{k}$ denotes the curvature vector of $\gamma$, it is defined by $\overrightarrow{k} = \frac{1}{|\gamma ^{\prime }|}\frac{\mathrm{{d}}}{\mathrm{{d}}u}\frac{\gamma ^{\prime }}{|\gamma ^{\prime }|}$, and $\gamma ^{\perp }$ denotes the normal projection of the position vector $\gamma$. This flow is known as the equivariant flow.

Definition 1.1

Let $\mathcal {C}$ be the set of antipodal invariant figure eight curves $\gamma : {\mathbb {C}}^1\rightarrow {\mathbb {C}}$ with only one self-intersection which is transversal and located at the origin.

Definition 1.2

Let $\Omega _{\alpha }$ be the antipodal invariant region in ${\mathbb {R}}^2$ bounded by two lines through the origin with angle between them equal to $\alpha$ (Fig. 1).

Fig. 1

Whitney sphere

Theorem 1.3

Let $\gamma$ be a curve in $\mathcal {C}$ satisfying at least one of the following assumptions:

• (i) $\{\gamma \}\cap {\mathbb {C}}^1(R)$ has at most 4 points for every $R>0$;

• (ii) $\{\gamma \}\subset \Omega _{\frac{\pi }{n}}$.

If $\{\gamma _t\}_{t\in [0,T)}$ is the maximal equivariant flow of $\gamma$, then $\gamma _T=\{0\}$. Moreover, the tangent flow at the origin is a line with multiplicity two.

Remark 1.4

The assumptions in Theorem 1.3 are sharp. In Sect. 3 we construct for every $\alpha >\frac{\pi }{2}$ a curve $\gamma \in \mathcal {C}$ such that $\{\gamma \}\subset \Omega _{\alpha }$ that develops a non-trivial singularity at the origin along the equivariant flow (1.1) when $n=2$.

The proof of Theorem 1.3 follows closely the ideas in [8, 9] where it is shown that singularities for the mean curvature flow of monotone Lagrangian submanifolds in ${\mathbb {R}}^4$ are modeled on area minimizing cones.

2 Preliminaries

Let L be a Lagrangian submanifold in ${\mathbb {C}}^n$. This implies that $\omega |_{L}=0$, where $\omega = \sum _{i=1}^{n}\frac{\sqrt{-1}}{2}\mathrm{{d}}z_i\wedge \overline{\mathrm{{d}}z_i}$ is the standard symplectic form on ${\mathbb {C}}^n$. Let $\Omega$ be the complex valued n-form given by

$$\begin{aligned} \Omega = \mathrm{{d}}z_1\wedge \ldots \wedge \mathrm{{d}}z_n. \end{aligned}$$

A standard computation implies that

$$\begin{aligned} \Omega |_L= e^{i\theta }vol_L. \end{aligned}$$

(2.1)

The multivalued function $\theta$ is called the Lagrangian angle of L. If $\theta$ is a single valued function, then L is called zero-Maslov class. If $\theta =\theta _0$, then L is calibrated by $\text {Re}(e^{-i\theta _0}\Omega )$ and hence area-minimizing. In this case, L is called special Lagrangian. More generally, the Lagrangian angle and the geometry of L are related through $\overrightarrow{H}= J(\nabla \theta )$. Recall also the Liouville one form given by

$$\begin{aligned} \lambda =\sum _{i=1}^{n}x_i\mathrm{{d}}y_i-y_i\mathrm{{d}}x_i. \end{aligned}$$

One can check that $\mathrm{{d}}\lambda =\omega$. In particular, $[\lambda ]\in H_1(L)$. When $[\lambda ]= c[\mathrm{{d}}\theta ]$ for some $c\in {\mathbb {R}}$, then L is said to be a monotone Lagrangian.

Let L be a equivariant Lagrangian submanifold in ${\mathbb {R}}^{2n}$. Hence, there exists a regular curve $\gamma$ in ${\mathbb {R}}^2$ such that

$$\begin{aligned} L=\left\{ (\gamma \, G_1,\ldots , \gamma \, G_n)\in {\mathbb {R}}^{2n},\, \sum _{i=1}^{n}G_i^2=1.\right\} \end{aligned}$$

(2.2)

After choosing a parametrization of $\gamma$ we have

$$\begin{aligned} \Omega _L:= \mathrm{{d}}z_1\wedge \cdots \wedge \mathrm{{d}}z_n\bigg |_{L}= e^{i\theta }\text {vol}_L=\frac{\gamma ^{\prime }}{|\gamma ^{\prime }|} \cdot \bigg (\frac{\gamma }{|\gamma |}\bigg )^{n-1} \text {vol}_L, \end{aligned}$$

(2.3)

where $z\cdot w$ denotes the standard multiplication of complex numbers; here we consider $\gamma$ as complex valued function. The Lagrangian angle relates to the geometry of L.

If $L_t$ is the mean curvature flow starting at L, then $L_t$ shares the same rotational symmetries of L, i.e., $L_t=\{\gamma _t G_1,\ldots , \gamma _t G_n):\, G=(G_1,\ldots ,G_n)\in {\mathbb {C}}^{n-1}\}$. Moreover,

$$\begin{aligned} \frac{\mathrm{{d}}\gamma }{\mathrm{{d}}t}=\overrightarrow{k}-(n-1) \frac{\gamma ^{\perp }}{|\gamma |^2}. \end{aligned}$$

(2.4)

Although the term $\frac{\gamma ^{\perp }}{|\gamma |^2}$ is not well defined at the origin the quantity has its meaning even when a curve goes through the origin as we can see below.

Lemma 2.1

Let $\gamma : [-a,a]\rightarrow {\mathbb {R}}^2$ a smooth regular curve such that $\gamma (0)=0$. Then

$$\begin{aligned} \lim _{s\rightarrow 0}\frac{\gamma ^{\perp }}{|\gamma |^2}(s)=\frac{1}{2}\overrightarrow{k}(0). \end{aligned}$$

Proof

Let us write the left hand side as

$$\begin{aligned}\frac{\gamma ^{\perp }}{|\gamma |^2}(s)= \frac{1}{|\gamma |^2}\left\langle \gamma , {i}\frac{\gamma ^{\prime }}{|\gamma ^{\prime }|}\right\rangle {i}\frac{\gamma ^{\prime }}{|\gamma ^{\prime }|}= \frac{s^2}{|\gamma |^2}\left\langle \frac{\gamma - s\gamma ^{\prime }(0)}{s^2}, {i}\frac{\gamma ^{\prime }}{|\gamma ^{\prime }|}\right\rangle {i}\frac{\gamma ^{\prime }}{|\gamma ^{\prime }|}. \end{aligned}$$

Using that $\lim _{s \rightarrow 0} \frac{\gamma (s)}{s}=\gamma ^{\prime }(0)$ and applying the L’Hopital’s rule twice, we obtain

$$\begin{aligned} \lim _{s\rightarrow 0}\frac{\gamma ^{\perp }}{|\gamma |^2}(s)= \frac{1}{2}\frac{1}{|\gamma ^{\prime }(0)|^2}\left\langle \gamma ^{\prime \prime }(0),i\frac{\gamma ^{\prime }(0)}{|\gamma ^{\prime }|(0)}\right\rangle i\frac{\gamma ^{\prime }(0)}{|\gamma ^{\prime }(0)|}= \frac{1}{2}\overrightarrow{k}(0). \end{aligned}$$

$\square$

Proposition 2.2

(Neves [10]) Let $\gamma _{i,t}:[-a,a]\rightarrow {\mathbb {R}}^2$, $i=1,2$ and $0\le t \le T$, smooth regular curves satisfying

• (1) $\gamma _{i,t}(-s)=-\gamma _{i,t}(s)$ for all $0\le t \le T$ and for every $s \in [-a,a]$ .

• (2) The curve $\gamma _{i,t}$, $i=1,2$, solves the equation

  $$\begin{aligned} \frac{\mathrm{{d}}\gamma }{\mathrm{{d}}t}=\overrightarrow{k}-(n-1)\frac{\gamma ^{\perp }}{|\gamma |^2}. \end{aligned}$$

• (3) $\gamma _{1,0}\cap \gamma _{2,0}=\{0\}$ (non-tangential intersection) and $\partial \gamma _{1,t}\cap \gamma _{2,t}=\partial \gamma _{2,t}\cap \gamma _{1,t}=\emptyset$ for all t.

Then for all $0\le t\le T$ we have $\gamma _{1,t}\cap \gamma _{2,t}=\{0\}$.

Proof

It suffices to restrict to what happens near the origin since the proposition follows from the standard maximum principle applied to the first time of tangential intersection.

First notice that $\gamma _{i,t}$ can be written as a graph on $[-\delta ,\delta ]$ for some $\delta >0$. Hence, $\gamma _{i,t}(s)=(s,f_{i,t}(s))$ and we define $h_{i,t}(s)=\frac{f_{i,t}(s)}{s}$. Let’s check that $h_{i,t}(s)$ is smooth: if $s\ne 0$, then

$$\begin{aligned} h^{\prime }(s)= \frac{f^{\prime }s-f}{s^2}\quad \text {and}\quad h''(s)= & {} \frac{(f''s+f'-f')s^2-(f's-f)2s}{s^4} \nonumber \\= & {} \frac{f''}{s} + 2\frac{f-f's}{s^3}. \end{aligned}$$

(2.5)

Since $f(0)=0$ and $f''(0)=0$ (item (1)), we can apply L’Hopital’s rule to show that $\alpha '$ and $\alpha ''$ in (2.5) have a limit when $s\rightarrow 0$. Hence, h is twice differentiable.

Finally we consider the function $u_t(s)=h_{1,t}-h_{2,t}$. Notice that $u_0>0$ by assumption (3) and $u_t(s)=u_t(-s)$. Recall that in the case of a graph $\gamma (s)=(s,f(s))$ we have

$$\begin{aligned} \gamma ^{\prime }=(1,f^{\prime }), \quad \nu =\frac{(f^{\prime },-1)}{\sqrt{1+(f^{\prime })^2}}\quad \text {and}\quad \overrightarrow{k}=-\frac{f^{\prime \prime }}{(1+(f^{\prime })^2)^{\frac{3}{2}}}\nu . \end{aligned}$$

Besides,

$$\begin{aligned} \frac{\gamma ^{\perp }}{|\gamma |^2}=\frac{sf^{\prime }-f}{s^2+f^2} \frac{1}{\sqrt{1+(f^{\prime })^2}}\nu . \end{aligned}$$

Therefore, the equation $\frac{\mathrm{{d}}\gamma }{\mathrm{{d}}t}^{\perp }=\overrightarrow{k}-(n-1)\frac{z^{\perp }}{|z|^2}$ implies

$$\begin{aligned} \frac{\mathrm{{d}}f}{\mathrm{{d}}t}=\frac{f^{\prime \prime }}{1+(f^{\prime })^2}+(n-1)\left( \arctan \frac{f}{s}\right) ^{\prime }. \end{aligned}$$

Standard computations imply that $h_{i,t}=\frac{f_{i,t}}{s}$ satisfies

$$\begin{aligned} \frac{\mathrm{{d}}\,h_{i,t}}{\mathrm{{d}}t}=\frac{h_{i,t}^{\prime \prime }}{1+(s\,h_{i,t}^{\prime }+h_{i,t})^2} + \frac{h_{i,t}^{\prime }}{s}\frac{2}{1+(s\,h_{i,t}^{\prime }+h_{i,t})^2} + (n-1)\frac{h_{i,t}^{\prime }}{s}\frac{1}{1+h_{i,t}^2}. \end{aligned}$$

Now we proceed to find the equation for $\frac{\mathrm{{d}}u_t}{\mathrm{{d}}t}$. Using that $\frac{h_{i,t}}{s}$ is also smooth, one can checked that

$$\begin{aligned} \frac{\mathrm{{d}}u_t}{\mathrm{{d}}t}=C_1^2 u_t^{\prime \prime }+C_2 u_t^{\prime } + C_3 u_t +C_4^2 \frac{u_t^\prime }{s}, \end{aligned}$$

where each $C_k$ is a smooth and bounded function. By item (3), the function $u_{t=0}$ is strictly positive since $\gamma _1$ and $\gamma _2$ have a non-tangential intersection at the origin.

Suppose $T_1$ is the first time where $u_t$ has a zero say at $s_0$. Hence, $s_0$ is a minimum point as $u_{T_1}\ge 0$. We consider the function $v_t=u_t e^{-Ct}+\varepsilon (t-T_1)$ where C is very large and $\varepsilon$ is a very small positive number. So at $(s_0,T_1)$ we have

$$\begin{aligned} 0\ge \frac{\mathrm{{d}}v_t}{\mathrm{{d}}t}(s_0,T_1)=\frac{\mathrm{{d}}u_t}{\mathrm{{d}}t}(s_0,T_1)e^{-CT_1}+\varepsilon \ge \varepsilon + C_4^2 \frac{u_t^{\prime }(s_0)}{s_0}e^{-CT_1}. \end{aligned}$$

We used in the equality part that $u_{T_1}(s_)=0$ and that $u_{T_1}^{\prime }(s_0)=0$ and $u_{T_1}^{\prime \prime }(s_)\le 0$ since $s_0$ is a minimum point for $u_{T_1}$. If $s_0\ne 0$ then the second term in the right hand side is zero and we get a contradiction. If $s_0=0$ then that term is just $u_t^{\prime \prime }(0)e^{-CT_1}$ by the L’Hopital’s rule, hence, non-negative and we obtain a contradiction again. $\square$

Corollary 2.3

The set $\mathcal {C}$ is preserved by the equivariant flow. Moreover, if $\gamma \in \mathcal {C}$ satisfies item (i) (respectively, item (ii)) in Theorem 1.3, then so does $\gamma _t$.

Proof

The symmetries of the curve $\gamma$ are preserved by the equivariant flow, hence $\gamma _t$ is also antipodal invariant. Proposition 2.2 guarantees that the only self intersection of $\gamma _t$ is at the origin and it is transversal for every t. Hence, $\mathcal {C}$ is preserved by the equivariant flow. Moreover, Proposition 2.2 also implies that $\gamma _t(s)$ can only intersect the line $s\overrightarrow{e^{i\beta }}_{s\in {\mathbb {R}}}$, with $\frac{\pi }{n}<\beta < \pi -\frac{\pi }{n}$, only at the origin for every $t \in [0,T)$. Therefore, if $\{\gamma \} \subset \Omega _{\frac{\pi }{n}}$, then $\{\gamma _t\}\subset \Omega _{\frac{\pi }{n}}$ also. Finally, by Theorem 1.3 in [2], the number of intersections between $\{\gamma \}$ and ${\mathbb {C}}^1(R)$ is non-increasing along the flow. $\square$

Lemma 2.4

If $\gamma \in \Omega _{\frac{\pi }{n}}$, then for every $t>0$ there exists $\delta _t>0$ such that $\{\gamma _t\}\subset \Omega _{\frac{\pi }{n}-\delta _t}$.

Proof

Since $\gamma \in \mathcal {C}$ is antipodal invariant and passes through the origin, one can check that $\lim _{s \rightarrow 0} \frac{\gamma ^{\perp }}{|\gamma |^2}(s)=0$, where $\gamma (s)$ is a local parametrization of $\gamma$ with $\gamma (s)=-\gamma (-s)$. By Lemma 2.1, we have that $\overrightarrow{k}(z_0)=\overrightarrow{k}(-z_0)=0$, where $\gamma (z_0)=\gamma (-z_0)=0$. Consequently, $\overrightarrow{H}(z_0)=\overrightarrow{H}(-z_0)=0$. This implies that $z_0$ and $-z_0$ are critical points of the Lagrangian angle $\theta _L$. It can be check easily that they correspond to local minimum and local maximum critical points. The strong maximum principle applied to $\frac{\mathrm{{d}}}{\mathrm{{d}}t}\theta = \Delta \theta$ implies that $\theta _t(z_0)< \theta (z_0)$ and $\theta _t(-z_0)> \theta (-z_0)$. $\square$

Let us use $\text {Area}(\gamma )$ to denote the area enclosed by $\gamma \in \mathcal {C}$. By the Stokes’ theorem we have that $\text {Area}(\gamma _t)=-\frac{1}{2}\int _{\gamma _t} \langle \gamma _t,\nu \rangle \mathrm{{d}}_{\gamma _t}$, where $\nu$ is the unit outward normal vector of $\gamma$.

Lemma 2.5

$$\begin{aligned} \pi (T-t)\le \text {Area}(\gamma _t)-\text {Area}(\gamma _T)\le 3\pi (T-t). \end{aligned}$$

Proof

Let $\gamma _t(u)$ be a parametrization of $\gamma _t$. Using that $\nu =i \frac{\gamma _t'}{|\gamma _t'|}$, we have that $\text {Area}(\gamma _t)=-\frac{1}{2}\int _{\gamma _t} \langle \gamma _t,i\,\gamma _t^{\prime }\rangle \mathrm{{d}}u$. Hence,

$$\begin{aligned} {\text {Area}}^{\prime }(t)= & {} -\frac{1}{2}\int _{\gamma _t} \bigg (\langle \partial _t \gamma , i\,\gamma _t^{\prime }\rangle + \langle \gamma , i\,(\partial _t\gamma )^{\prime } \rangle \bigg ) \mathrm{{d}}u \\= & {} -\frac{1}{2}\int _{\gamma _t}\bigg (\langle \partial _t \gamma , i\,\gamma _t^{\prime }\rangle + \langle \gamma _t,i\partial _t\gamma \rangle ^{\prime } - \langle \gamma ^{\prime },i\,\partial _t\gamma \rangle \bigg )\mathrm{{d}}u \\= & {} -\int _{\gamma _t}\langle \partial _t \gamma , i\,\gamma _t^{\prime }\rangle \, \mathrm{{d}}u -\frac{1}{2}\int _{\gamma _t}\langle \gamma _t,i\partial _t\gamma \rangle ^{\prime }\,\mathrm{{d}}u = -\int _{\gamma _t}\langle \partial _t \gamma , \nu \rangle \, \mathrm{{d}}\gamma _t. \end{aligned}$$

The last equality follows from the Fundamental Theorem of Calculus. Hence,

$$\begin{aligned} {\text {Area}}'(t)=-\int _{\gamma _t}\bigg < \overrightarrow{k} -(n-1)\frac{z^{\perp }}{|z|^2}, \nu \bigg >\, \mathrm{{d}}_{\gamma _t}=-\int _{\gamma _t}\langle \overrightarrow{k}, \nu \rangle \mathrm{{d}}_{\gamma _t}. \end{aligned}$$

The last equality follows from the Divergence Theorem applied to vector field $X= \frac{z}{|z|^2}$ and the fact that $z=0$ is not in the interior of the region enclosed by $\gamma _t$. Combining the Gauss–Bonnet theorem and the fact that the exterior angle $\alpha _t$ of $\gamma _t$ at the origin is in $[-\pi ,\pi ]$ we obtain

$$\begin{aligned} \int _{\gamma _t}\langle \overrightarrow{k},-\nu \rangle \mathrm{{d}}_{\gamma _t} + \alpha _t=2\pi \Longrightarrow \pi \le \int _{\gamma _t}\langle \overrightarrow{k},-\nu \rangle \mathrm{{d}}_{\gamma _t} \le 3\pi . \end{aligned}$$

Therefore, $-3\pi \le \text {Area}^{\prime }(\gamma _t)\le -\pi$. The Lemma now follows if we integrate this quantity from t to T. $\square$

3 Proof of the Theorem

Let $L_t$ be a solution of the mean curvature flow starting on a k-dimensional submanifold L in ${\mathbb {R}}^m$. Consider the backward heat kernel

$$\begin{aligned} \Phi _{x_0,T}(x,t)= \frac{1}{(4\pi (T-t))^{\frac{k}{2}}}e^{-\frac{|x-x_0|^2}{4(T-t)}}. \end{aligned}$$

The following formula is known as the Huisken’s monotonicity formula:

$$\begin{aligned}&\frac{\mathrm{{d}}}{\mathrm{{d}}t}\int _{L_t} f_t \Phi _{x_0,T}\mathrm{{d}}{\mathcal {H}}^k \nonumber \\&\quad =\int _{L_t} \bigg (\frac{\mathrm{{d}}}{\mathrm{{d}}t}f_t - \Delta f_t - \bigg |H- \frac{(x-x_0)^{\perp }}{2(T-t)}\bigg |^2f_t \bigg )\Phi _{x_0,T} \mathrm{{d}}{\mathcal {H}}^k, \end{aligned}$$

(3.1)

where $d{{\mathcal {H}}}^k$ denotes the k-dimensional Hausdorff measure.

Recall that if $\{L_t\}_{t\in [0,T)}$ is the Lagrangian mean curvature flow starting at L, then

$$\begin{aligned} L_s^{\sigma }=\sigma \,\left( L_{T+\frac{s}{\sigma ^2}}-x_0\right) , \end{aligned}$$

for $s \in [-T\lambda ^2,0)$, also satisfies the Lagrangian mean curvature flow and is referred as the tangent flow at $x_0$. The following is a restatement of Theorem 1.3:

Theorem 3.1

Let $\gamma$ be a curve in $\mathcal {C}$ which satisfies at least one of the following assumptions

• (i) $\{\gamma \}\cap {\mathbb {C}}^1(R)$ has at most 4 points for every $R>0$;

• (ii) $\{\gamma \}\subset \Omega _{\frac{\pi }{n}}$.

If $\{\gamma _t\}_{t\in [0,T)}$ is the maximal equivariant flow of $\gamma$, then $\gamma _T=\{0\}$. Moreover, the tangent flow at the origin is a line with multiplicity two.

Proof

Let us prove first that if $z=0$ is a singular point, then $\gamma _T=\{0\}$. Arguing by contradiction, we assume that $z=0$ is a singular point for $\{\gamma _t\}_{0\le t<T}$ and $\gamma _T\ne \{0\}$. Given $\sigma _i\rightarrow \infty$, let $\gamma _s^{i}=\sigma _i \gamma _{T+\frac{s}{\sigma _i^2}}$.

Lemma 3.2

Let a and b real numbers such that $a<b<0$. Then

$$\begin{aligned} \lim _{i\rightarrow \infty }\int _{a}^{b}\int _{\gamma _s^i\cap A(\frac{1}{\eta },\eta ,0)} \bigg (|\overrightarrow{k}|^2+|\gamma ^{\perp }|^2\bigg )\,\mathrm{{d}}{\mathcal {H}}^1 ds=0, \end{aligned}$$

where $A(\frac{1}{\eta },\eta ,0)$ is an annulus centered at $z=0$ with inner and outer radius $\eta$ and $\frac{1}{\eta }$, respectively.

Proof

Let $L_s^i$ be the immersed Lagrangian sphere in ${\mathbb {C}}^2$ obtained via $L_s^i=(\gamma _s^iG_1,\ldots ,\gamma _s^iG_n)$. It is proved in Lemma 5.4 in [8] that

$$\begin{aligned} \lim _{i\rightarrow \infty }\int _{a}^{b}\int _{L_s^i\cap B_R(0)} \bigg (|H|^2+|x^{\perp }|^2\bigg )\, \mathrm{{d}}{\mathcal {H}}^n(x)ds=0, \end{aligned}$$

(3.2)

where H is the mean curvature vector of $L_s^i$. For the convenience of the reader let us recall the proof of this fact. It is a standard computation to check that the Lagrangian angle $\theta$ obeys the following evolution equation $\frac{\mathrm{{d}}}{\mathrm{{d}}t}\theta _{i,s}^2= \Delta \theta _{i,s}^2 - 2|H|^2$. Applying (3.1) with $f_t= \theta _{i,s}^2$ and $f_t=1$, we obtain

$$\begin{aligned} \frac{\mathrm{{d}}}{\mathrm{{d}}s} \int _{L_s^i} \theta _{i,s}^2 \Phi \mathrm{{d}}{\mathcal {H}}^n= & {} \int _{L_s^i}\bigg (-2 |H|^2 - \bigg |H- \frac{x^{\perp }}{2s}\bigg |^2 \theta _{i,s}^2\bigg ) \Phi \, \mathrm{{d}}{\mathcal {H}}^n \end{aligned}$$

(3.3)

$$\begin{aligned} \frac{\mathrm{{d}}}{\mathrm{{d}}s} \int _{L_s^i} \Phi \mathrm{{d}}{\mathcal {H}}^n= & {} \int _{L_s^i} - \bigg |H- \frac{x^{\perp }}{2s}\bigg |^2\Phi \, \mathrm{{d}}{\mathcal {H}}^n, \end{aligned}$$

(3.4)

respectively. Integrating (3.3) from a to b gives

$$\begin{aligned} 2\lim _{i \rightarrow \infty }\int _{a}^{b}\int _{L_s^i} |H|^2\, \Phi \, \mathrm{{d}}{\mathcal {H}}^n ds\le & {} \lim _{i\rightarrow \infty }\int _{L_b^i} \theta _{i,b}^2 \Phi \,\mathrm{{d}}{\mathcal {H}}^n - \lim _{i\rightarrow \infty }\int _{L_a^i} \theta _{i,a}^2 \Phi \,\mathrm{{d}}{\mathcal {H}}^n =0. \end{aligned}$$

The last inequality follows from the scale invariance and monotonicity of $\int _{L_t}\theta ^2\, \Phi \mathrm{{d}}{\mathcal {H}}^n$. Similarly, we obtain

$$\begin{aligned} \lim _{i \rightarrow \infty }\int _{a}^{b}\int _{L_s^i} \bigg |H- \frac{x^{\perp }}{2s}\bigg |^2\, \Phi \, \mathrm{{d}}{\mathcal {H}}^n ds= \lim _{i\rightarrow \infty }\int _{L_b^i} \Phi \,\mathrm{{d}}{\mathcal {H}}^2 - \lim _{i\rightarrow \infty }\int _{L_a^i} \Phi \,\mathrm{{d}}{\mathcal {H}}^n=0. \end{aligned}$$

It follows from the triangular inequality that

$$\begin{aligned} \lim _{i \rightarrow \infty }\int _{a}^{b}\int _{L_s^i} \bigg |\frac{x^{\perp }}{2s}\bigg |^2\, \Phi \, \mathrm{{d}}{\mathcal {H}}^n \mathrm{{d}}s=0. \end{aligned}$$

This completes the proof of (3.2). As $|H|^2=|\overrightarrow{k}-(n-1)\frac{\gamma ^{\perp }}{|\gamma |^2}|^2$ and $|x^{\perp }|^2=|\gamma ^{\perp }|^2$, we obtain for each $\eta >0$ that

$$\begin{aligned} \lim _{i\rightarrow \infty }\int _{a}^{b}\int _{\gamma _s^i\cap A(\frac{1}{\eta },\eta ,0)} \bigg (|\overrightarrow{k}|^2+|\gamma ^{\perp }|^2\bigg )\mathrm{{d}}{\mathcal {H}}^1 \mathrm{{d}}s=0. \end{aligned}$$

$\square$ From previous lemma it follows that for almost every $s\in (a,b)$ that

$$\begin{aligned} \lim _{i\rightarrow \infty }\int _{\gamma _s^i\cap A(\frac{1}{\eta },\eta ,0)} \bigg (|\overrightarrow{k}|^2+|\gamma ^{\perp }|^2\bigg )\mathrm{{d}}{\mathcal {H}}^1=0. \end{aligned}$$

This implies that $\gamma _s^{i}$ converges to a union of lines in $C_{loc}^{1,\frac{1}{2}}({\mathbb {R}}^2-\{0\})$. In fact, each connected component of $\gamma _s^i$ inside $B_R(0)-\{0\}$ converge to a line segment with multiplicity one since the convergence is in $C_{loc}^{1,\frac{1}{2}}({\mathbb {R}}^2-\{0\})$.

Assume first that $\gamma$ satisfies item i), then by Proposition 2.2 and Corollary 2.3, the curve $\gamma _s^{i}$ in $B_R(0)-\{0\}$ has two embedded connected components. Hence, each converges to a line segment with multiplicity one in $B_R(0)-\{0\}$. Equivalently, in a neighborhood of the origin $L_t$ is a union of two smooth embedded discs intersecting transversally at a interior point. Hence, each piece of $L_s^{i}$ converges weakly to a plane with multiplicity one. Since $\gamma _T\ne \{0\}$, we can talk about the localized Gaussian density of each connected component of $L_t\cap B_r(0)$ computed at (0, T) which will be very close to one. Applying White’s Local Regularity Theorem, see localized version Theorem 5.6 in [4]), to each component of $L_t\cap B_r(0)$, we conclude that the origin is not a singularity of $\{L_t\}_{t\in [0,T)}$, contradiction.

To handle other connected components of $\gamma _s^i$ in $B_{4R}(0)$ we study the Lagrangian angle $\theta _s^i$. Let $\beta$ be a primitive of $\lambda _L$. It is proved in [9] that $\nabla \beta = J(x^{\perp })$ and $\frac{\mathrm{{d}}}{\mathrm{{d}}t}\beta = \Delta \beta - 2\theta$. This implies that the function $u= \beta + 2(t-t_0)\theta$ satisfies $\frac{\mathrm{{d}}}{\mathrm{{d}}t}f(u)= \Delta f(u) - f^{\prime \prime }(u)|x^{\perp }+ 2(t-t_0)H|^2$, where $f\in C_0^{\infty }({\mathbb {R}})$. Plugging the function f(u) in (3.1), we obtain

$$\begin{aligned} \frac{\mathrm{{d}}}{\mathrm{{d}}s}\int _{L_s^i} f(u_s^i) \Phi = - \int _{L_s^i} \bigg |H- \frac{x^{\perp }}{2s} \bigg |^2f(u_s^i) \, \Phi \, + f^{\prime \prime }(u_s^i)\bigg |x^{\perp }+ 2(s-s_0)H\bigg |^2\Phi . \end{aligned}$$

Integrating this formula from $-1$ to $s_0$ and using (3.2) , we obtain

$$\begin{aligned} \lim _{i \rightarrow \infty } \int _{L_{s_0}^i\cap B_{4R}(0)} f(\beta _{s_0}^i)\Phi \, =\, \lim _{i \rightarrow \infty } \int _{L_{-1}^i\cap B_{4R}(0)} f(\beta _{-1}^i - 2(1 + s_0)\theta _{-1}^i)\Phi . \end{aligned}$$

Let $\gamma ^i$ be a connected component of $\gamma _s^i$ in $B_{4R}(0)$ that intersects $B_R(0)$ and does not passes through the origin. Since $|\nabla f(\beta _s^i)|$ is bounded, there exists a constant $b_{s_0}$ such that $\lim _{i \rightarrow \infty } f(\beta _{s_0}^i)=f(b_{s_0})$. Similarly, $\lim _{i \rightarrow \infty } f(\beta _{-1}^i)=f(b_{-1})$. As before, $\gamma _i$ converges in $C^{1,\frac{1}{2}}({\mathbb {R}}^2-\{0\})$ to lines $l_{\overrightarrow{v_1^s}}$ and $l_{\overrightarrow{v_2^s}}$ in the direction of the vectors $\overrightarrow{v_i^s}$. Moreover,

$$\begin{aligned} \lim _{i \rightarrow \infty } \int _{\gamma ^i} f(\beta _{-1}^i - 2(1 + s_0)\theta _{-1}^i)\Phi \,\mathrm{{d}}{\mathcal {H}}^1= \sum _{i=1}^{2}\int _{l_{\overrightarrow{v_i}}} f(b_{-1}- 2(1+s_0)\theta _i)\Phi \,\mathrm{{d}}{\mathcal {H}}^1. \end{aligned}$$

Note that (2.3) implies that $\theta _s^i$ converge to a constant in each connected component of $\gamma _s^i\cap (B_R(0)-B_r(0))$. We claim that $\theta _1=\theta _2$. Otherwise, by choosing f with support near $b_{s_0}$ and equal to 1 near $b_{s_0}$, we obtain

$$\begin{aligned} \sum _{i=1}^{2}\int _{l_{\overrightarrow{v_i}}\cap B_R(0)} \Phi \,\mathrm{{d}}{\mathcal {H}}^1= \int _{l_{\overrightarrow{v_{i_0}}}\cap B_R(0)} \Phi \,\mathrm{{d}}{\mathcal {H}}^1, \end{aligned}$$

contradiction.

Let us assume that $\gamma$ satisfies item (ii). In this case, $\gamma _s^i\cap B_{4R}(0)$ has a connected component $\gamma ^i$ intersecting $B_{2R}$ which converges in $C^{1,\frac{1}{2}}(B_R(0)-\{0\})$ to the lines $\gamma _A$ and $\gamma _B$ with multiplicity one. Moreover, $\theta _s^i$ converge to a constant $\theta _0$ on each connected component of $\gamma ^i \cap (B_R(0)-B_r(0))$. This implies that $\gamma _A=\gamma _B$ with the same orientation or the angle between $\gamma _A$ and $\gamma _B$ is $\frac{\pi }{n}$. The first case cannot happen since $I_2(\beta _s^i, {\mathbb {C}}^1(0, r))= 0$, where $I_2(\cdot , \cdot )$ is the intersection number mod 2. The second case cannot happen since $\{\gamma _t\}\subset \Omega _{\frac{\pi }{n}- \delta _t}$ by Lemma 2.4. Hence, the origin is not a singularity if we assume that $\gamma _T\ne \{0\}$.

On the other hand, no singularities away from the origin occur. Indeed, in [11] Oaks complement the work of Angenent on singularities of equations of type $\frac{\mathrm{{d}}}{\mathrm{{d}}t}\gamma _t= V(\overrightarrow{T},k)\overrightarrow{N}$ by showing that near the singularity the curve $\gamma _t$ must lose a self intersection. Since Proposition 2.2 asserts the only self intersection of $\gamma _t$ is at the origin we are done.

Now let us prove that the tangent flow at the singular point is a line through the origin with multiplicity 2. For this we choose a sequence of scale factors $\lambda _i \rightarrow +\infty$ and we set $\gamma _{s}^i=\lambda _i\gamma _{T+\frac{s}{\lambda _i^2}}$ defined in $[-T\lambda _i^2,0)$.

As discussed before $\gamma _s^i$ converges in $C_{\text {loc}}^{1,\frac{1}{2}}({\mathbb {R}}^2-\{0\})$ to a union of two lines through the origin for almost every s fixed. Let us denote them by $l_A$ and $l_B$. As $\text {Area}(\gamma _t)$ is going to zero there exist a unique $t_i\in [0,T)$ for which $\text {Area}(\gamma _{t_i})=\frac{1}{\lambda _i^2}$. This implies that $\text {Area}(\gamma _{s_1^i}^i)=1$, where $s_1^i$ is given by $s_1^i=-\lambda _i^2(T-t_i)$. Since $\pi (T-t)\le A(t)\le 3\pi (T-t)$ by Lemma 2.5, we obtain that $s_1^i \in [-\frac{1}{\pi },-\frac{1}{3\pi }]$. In particular, if $s^{*}=-\frac{1}{3\pi }$, then $\limsup _{i \rightarrow \infty }\text {Area}(\gamma _{s^{*}}^i)\le 1$. Therefore, $\gamma _{s^{*}}^i$ must converge to $2\gamma _A+ 2\gamma _B$ or $\gamma _A=\gamma _B$ since $\gamma _{s^{*}}^i$ is becoming non-compact enclosing bounded area.

The first case does not happen as it violates the assumptions (i) and (ii) as discussed above. $\square$

The next example constructs equivariant Lagrangian spheres in ${\mathbb {R}}^4$ that do not collapse to a point along the mean curvature flow.

Example 3.3

Let $\gamma _0$ be the curve $\gamma ^{\alpha }(u)=\sin (\frac{\pi u}{\alpha })^{-\frac{\alpha }{\pi }}(\cos (u),\sin (u))$ with $u \in {\mathbb {R}}$. The existence of a solution of the equivariant flow starting at $\gamma ^{\alpha }$ is given in [8], let us denote it by $\{\gamma _t\}_{t\in [0,T_{\alpha })}$. It is shown in [8] that when $\alpha >\frac{\pi }{2}$, then $T_{\alpha }<\infty$ and $\gamma _t$ develops a singularity at the origin. When $\alpha \in (0,\pi )$, then $\gamma ^{\alpha }$ is contained in $\Omega _{\alpha }$ and it is asymptotic to its boundary. Consider the region $U_{\alpha }$ in $\Omega _{\alpha }$ that is bounded by $\{\gamma ^{\alpha }\}\cup \{-\gamma ^{\alpha }\}$. One can check that $U_{\alpha }$ has infinite area. Choose $\beta \in \mathcal {C}$ contained in $U_{\alpha }$ whose area enclosed, $\text {Area}(\beta )$, is greater than $3\pi \, T_{\alpha }$. See Fig. 2 for the case $\alpha =\pi$. Let $\{\beta _t\}_{t\in [0,T)}$ be the solution of the equivariant flow starting at $\beta$. By the avoidance principle, $\beta _t$ and $\gamma _t$ do not intersect. Hence, $T<T_{\alpha }$. On the other hand, by Lemma 2.5 we have that $\text {Area}(\beta _{T})\ge \text {Area}(\beta )- 3\pi T\ge 3\pi (T_{\alpha }-T)>0$. Therefore, a non trivial singularity must occur at the origin.

Fig. 2

Curve $\beta$

Let us show that any Type II dilation of $\gamma _t$ near the singularity converges to an eternal solution of curve shortening flow. As in Chapter 4 in [7], there exist for each $k>0$, points $z_k\in \gamma _t({\mathbb {C}}^1)$, $t_k\in [0, T-\frac{1}{k}]$, and scaling $\lambda _k>0$ such that $\beta _s^k= \lambda _k (\gamma _{T+\frac{s}{\lambda _k^2}}-z_k)$ satisfies

$$\begin{aligned} \frac{\mathrm{{d}}}{\mathrm{{d}}s}\beta _s^k= \overrightarrow{k}(\beta _s^k)- (n-1)\frac{(\beta _s^k+ \lambda _k z_k)^{\perp }}{|\beta _s^k+ \lambda _k z_k|^2}, \end{aligned}$$

where $s\in (a_k,b_k)$. Moreover, $\lim _{k\rightarrow \infty }a_k=-\infty$, $\lim _{k\rightarrow \infty }b_k=\infty$, and $0< \lim _{k\rightarrow \infty }\sup _{(a_k,b_k)\times {\mathbb {C}}^1}|\overrightarrow{k}(\beta _s^k)|\le C$. It is proved that $\beta _s^k$ converge smoothly as $k\rightarrow \infty$ to a non-compact flow $(\beta _s)_{s\in {\mathbb {R}}}$. We claim that $\lim _{k\rightarrow \infty } \lambda _k z_k = \infty$. If not, then we could replace the points $z_k$ by $z=0$ and obtain the same conclusion. This is impossible since central dilations converge to lines. Therefore, as $k\rightarrow \infty$,

$$\begin{aligned} \frac{\mathrm{{d}}}{\mathrm{{d}}s} \beta _s= \overrightarrow{k}(\beta _s). \end{aligned}$$