Abstract
We prove that the modular component  , constructed in the Main Theorem in Fania and Flamini (Adv Math 436:109409, 2024. https://doi.org/10.1016/j.aim.2023.109409), of Ulrich vector bundles of rank r and given Chern classes, on suitable threefold scrolls \(X_e\) over Hirzebruch surfaces \({\mathbb {F}}_{e\ge 0}\), which arise as tautological embeddings of projectivization of very-ample vector bundles on \({\mathbb {F}}_e\), is generically smooth, irreducible and unirational. A stronger result holds for the suitable associated moduli space
, constructed in the Main Theorem in Fania and Flamini (Adv Math 436:109409, 2024. https://doi.org/10.1016/j.aim.2023.109409), of Ulrich vector bundles of rank r and given Chern classes, on suitable threefold scrolls \(X_e\) over Hirzebruch surfaces \({\mathbb {F}}_{e\ge 0}\), which arise as tautological embeddings of projectivization of very-ample vector bundles on \({\mathbb {F}}_e\), is generically smooth, irreducible and unirational. A stronger result holds for the suitable associated moduli space  of vector bundles of rank r and given Chern classes on \({\mathbb {F}}_e\), Ulrich w.r.t. the very ample polarization
of vector bundles of rank r and given Chern classes on \({\mathbb {F}}_e\), Ulrich w.r.t. the very ample polarization  which turns out to be generically smooth, irreducible and unirational.
which turns out to be generically smooth, irreducible and unirational.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let X be a smooth irreducible projective variety of dimension \(n \ge 1\), polarized by a very ample divisor H on X. The existence of vector bundles  on X which are Ulrich with respect to
on X which are Ulrich with respect to  has interested various authors.
has interested various authors.
For some specific classes of varieties such problem has being attacked, see for instance [1, 2, 9,10,11, 13]. Whenever such bundles do exist, since they are always semistable (in the sense of Gieseker-Maruyama, cf. also § 1 below) and also slope-semistable (cf. [6, Def. 2.7, Thm. 2.9-(a)]), one is interested in knowing if these bundles are also stable, equivalently slope-stable (cf. [6, Def. 2.7, Thm. 2.9-(c)]). Furthermore, from their semi-stability, such rank-r vector bundles give rise to points in a moduli space, say \(M:= M^{ss}(r; c_1, c_2, \ldots , c_k)\), where \(k:= \textrm{min} \{r,\,n\}\), parametrizing (S-equivalence classes of) semistable sheaves of given rank r and given Chern classes \(c_i\) on X, \(1 \le i \le k\) (cf. [6, p. 1250083-9]). Therefore, one is also interested e.g. in understanding: whether M contains at least an irreducible component, say  , which is generically smooth, i.e. reduced, or even smooth; to which sheaf on X corresponds the general point of such a component
, which is generically smooth, i.e. reduced, or even smooth; to which sheaf on X corresponds the general point of such a component  ; what can be said about the birational geometry of
; what can be said about the birational geometry of  , namely if it is perhaps rational/unirational; finally, if by chance M turns out to be also irreducible, that is,
, namely if it is perhaps rational/unirational; finally, if by chance M turns out to be also irreducible, that is,  .
.
In this paper we are interested in some of the aforementioned properties for the moduli spaces of Ulrich vector bundles on a variety \(X_e\) which is a 3-fold scroll over a Hirzebruch surface \({\mathbb {F}}_e\), with \(e \ge 0\). More precisely on 3-fold scrolls \(X_e\) arising as embedding, via very-ample tautological line bundles  , of projective bundles
, of projective bundles  over \({\mathbb {F}}_e\), where
over \({\mathbb {F}}_e\), where  are very-ample rank-2 vector bundles on \({\mathbb {F}}_e\) with Chern classes
are very-ample rank-2 vector bundles on \({\mathbb {F}}_e\) with Chern classes  numerically equivalent to \(3 C_e + b_ef\) and
numerically equivalent to \(3 C_e + b_ef\) and  , where \(C_e\) and f are, as customary, generators of \(\textrm{Num}({\mathbb {F}}_e)\) as in [14, V, Prop. 2.3] and where \(b_e\) and \(k_e\) are integers satisfying some natural numerical conditions. We will set
, where \(C_e\) and f are, as customary, generators of \(\textrm{Num}({\mathbb {F}}_e)\) as in [14, V, Prop. 2.3] and where \(b_e\) and \(k_e\) are integers satisfying some natural numerical conditions. We will set  the hyperplane line bundle of the embedded 3-fold scroll, which we will also call tautological polarization of \(X_e\), as
the hyperplane line bundle of the embedded 3-fold scroll, which we will also call tautological polarization of \(X_e\), as  .
.
The existence of Ulrich bundles on such threefolds \(X_e\) has been considered in [13], where it was proved that \(X_e\) does not support any Ulrich line bundle w.r.t. \(\xi \), unless \(e = 0\). As to Ulrich vector bundles of rank \(r \ge 2\), it was proved in [13] that the moduli space M, in the above sense, arising from rank-r vector bundles  on \(X_{e\ge 0}\) which are Ulrich w.r.t. \(\xi \) and with first Chern class
on \(X_{e\ge 0}\) which are Ulrich w.r.t. \(\xi \) and with first Chern class

is not empty and it contains a generically smooth component  of dimension
of dimension

The general point  has been proved to correspond to a slope-stable vector bundle, of slope w.r.t. \(\xi \) given by
has been proved to correspond to a slope-stable vector bundle, of slope w.r.t. \(\xi \) given by  (see Theorem 2.5 below, for more details).
(see Theorem 2.5 below, for more details).
As a consequence of such result and a natural one-to-one correspondence among rank-r vector bundles on \(X_e\), of the form  , which are Ulrich w.r.t. \(\xi \) on \(X_e\), and rank-r vector bundles on \({\mathbb {F}}_e\), of the form
, which are Ulrich w.r.t. \(\xi \) on \(X_e\), and rank-r vector bundles on \({\mathbb {F}}_e\), of the form  , which are Ulrich w.r.t.
, which are Ulrich w.r.t.  , in [13] we have deduced Ulrichness results for vector bundles on the base surface \({\mathbb {F}}_e\) with respect to naturally associated very ample polarization
, in [13] we have deduced Ulrichness results for vector bundles on the base surface \({\mathbb {F}}_e\) with respect to naturally associated very ample polarization  , see Theorem 2.6 for more details.
, see Theorem 2.6 for more details.
By a result of Antonelli, [1, Theorem 1.2], if  is a rank-r vector bundle on \({\mathbb {F}}_e\) which is Ulrich with respect to a very ample polarization of the form
is a rank-r vector bundle on \({\mathbb {F}}_e\) which is Ulrich with respect to a very ample polarization of the form  and with
and with  , then
, then  must fit into a short exact sequence of the form
must fit into a short exact sequence of the form

where \(\gamma , \delta \) and \(\tau \) are suitably defined by \(r, \alpha , \beta , a, b, e\) (cfr. (3.1)). This fact will be useful in the present note to give further information about our modular components  as in [13]. Our main results in this paper are the following
as in [13]. Our main results in this paper are the following
Theorem A
(cf. Theorem 3.2, below) For any integer \(e \ge 0\), let \({\mathbb {F}}_e\) be the Hirzebruch surface and let  denote the line bundle \(\alpha C_e + \beta f\) on \({\mathbb {F}}_e\), where \(C_e\) and f are generators of \(\textrm{Num}({\mathbb {F}}_e)\) (cf. [14, V, Prop. 2.3]). Let \((X_e, \xi )\) be a 3-fold scroll over \({\mathbb {F}}_e\) as above, where \(\varphi : X_e \rightarrow {\mathbb {F}}_e\) denotes the scroll map. Then the moduli space of rank-\(r\ge 2\) vector bundles
denote the line bundle \(\alpha C_e + \beta f\) on \({\mathbb {F}}_e\), where \(C_e\) and f are generators of \(\textrm{Num}({\mathbb {F}}_e)\) (cf. [14, V, Prop. 2.3]). Let \((X_e, \xi )\) be a 3-fold scroll over \({\mathbb {F}}_e\) as above, where \(\varphi : X_e \rightarrow {\mathbb {F}}_e\) denotes the scroll map. Then the moduli space of rank-\(r\ge 2\) vector bundles  on \(X_e\) which are Ulrich w.r.t. \(\xi \) and with first Chern class
on \(X_e\) which are Ulrich w.r.t. \(\xi \) and with first Chern class

is not empty and it contains a generically smooth component  , which is of dimension
, which is of dimension

(see Theorem 2.5) and which is moreover unirational.
For the moduli space of rank-\(r \ge 2\) bundles on \({\mathbb {F}}_e\), the base of the scroll \(X_e\), which are Ulrich w.r.t. the polarization  , a stronger result holds; precisely
, a stronger result holds; precisely
Theorem B
(cf. Theorem 3.1, below) Let  be the moduli space of rank-r vector bundles
be the moduli space of rank-r vector bundles  on \({\mathbb {F}}_e\) which are Ulrich w.r.t.
on \({\mathbb {F}}_e\) which are Ulrich w.r.t.  and with first Chern class
and with first Chern class

Then  is generically smooth, of dimension
is generically smooth, of dimension

(see Theorem 2.6) and moreover it is irreducible and unirational.
The above theorems extend unirationality results in [1] and [9].
The paper is structured as follows. In Sect. 1 we fix notation and terminology. In Sect. 2 we recall some of the known results that we will use throughout the paper. In Sect. 3 we state and prove our new main results.
2 Notation and terminology
In this paper we work over \({\mathbb {C}}\). All schemes will be endowed with the Zariski topology. We will interchangeably use the terms rank-r vector bundle on a smooth, projective variety X and rank-r locally free sheaf. In particular, sometimes, to ease some formulas, with a small abuse of notation we identify divisor classes with the corresponding line bundles, interchangeably using additive and tensor-product notation. The dual bundle of a rank-r vector bundle  on X will be denoted by
on X will be denoted by  ; thus, if L is of rank-1, i.e. it is a line bundle, we interchageably use \(L^{\vee }\) or \(-L\). If M is a moduli space, parametrizing objects modulo a given equivalence relation, and if Y is a representative of an equivalence class in M, we will denote by \([Y] \in M\) the point corresponding to Y. For non-reminded general terminology, we refer the reader to [14]).
; thus, if L is of rank-1, i.e. it is a line bundle, we interchageably use \(L^{\vee }\) or \(-L\). If M is a moduli space, parametrizing objects modulo a given equivalence relation, and if Y is a representative of an equivalence class in M, we will denote by \([Y] \in M\) the point corresponding to Y. For non-reminded general terminology, we refer the reader to [14]).
Because our object will be Ulrich bundles, we recall their definition and basic properties.
Definition 1.1
Let \(X\subset {\mathbb {P}}^N\) be a smooth, irreducible, projective variety of dimension n and let H be a hyperplane section of X. A vector bundle  on X is said to be Ulrich with respect to
on X is said to be Ulrich with respect to  if
if

Definition 1.2
Let \(X\subset {\mathbb {P}}^N\) be a smooth, irreducible, projective variety of dimension n polarized by  , where H is a hyperplane section of X, and let
, where H is a hyperplane section of X, and let  be a rank-2 vector bundle on X which is Ulrich with respect to
be a rank-2 vector bundle on X which is Ulrich with respect to  . Then \({\mathcal {U}}\) is said to be special if
. Then \({\mathcal {U}}\) is said to be special if  .
.
For the reader’s convenience, we briefly remind facts concerning (semi)stability and slope-(semi)stability properties of Ulrich bundles as in [6, Def. 2.7]. Let X be a smooth, irreducible, projective variety and let  be a vector bundle on X; recall that
be a vector bundle on X; recall that  is said to be semistable (in the sense of Gieseker-Maruyama) if for every non-zero coherent subsheaf
is said to be semistable (in the sense of Gieseker-Maruyama) if for every non-zero coherent subsheaf  , with
, with  , the inequality
, the inequality  holds true, where
holds true, where  and
and  are the Hilbert polynomials of the sheaves. Furthermore,
are the Hilbert polynomials of the sheaves. Furthermore,  is stable if strict inequality above holds. Similarly, recall that the slope of a vector bundle
is stable if strict inequality above holds. Similarly, recall that the slope of a vector bundle  (w.r.t. a given polarization
(w.r.t. a given polarization  on X) is defined to be
on X) is defined to be  ; the bundle
; the bundle  is said to be \(\mu \)-semistable, or even slope-semistable, if for every non-zero coherent subsheaf
is said to be \(\mu \)-semistable, or even slope-semistable, if for every non-zero coherent subsheaf  with
with  , one has
, one has  . The bundle
. The bundle  is \(\mu \)-stable, or slope-stable, if strict inequality holds.
is \(\mu \)-stable, or slope-stable, if strict inequality holds.
The two definitions of (semi)stability are in general related as follows (cf. e.g. [6, § 2]):
If  is in particular a rank-r vector bundle which is Urlich w.r.t.
is in particular a rank-r vector bundle which is Urlich w.r.t.  , then
, then  is always semistable, so also slope-semistable (cf. [6, Thm. 2.9-(a)]); moreover, for
is always semistable, so also slope-semistable (cf. [6, Thm. 2.9-(a)]); moreover, for  the notions of stability and slope-stability coincide (cf. [6, Thm. 2.9-(c)]).
the notions of stability and slope-stability coincide (cf. [6, Thm. 2.9-(c)]).
As for the projective variety which will be the support of Ulrich bundles we are interested in, throughout this work we will denote it by \(X_e\) and it will be a 3-dimensional scroll over the Hirzebruch surface  , with \(e \ge 0\) an integer.
, with \(e \ge 0\) an integer.
More precisely, let \(\pi _e: {\mathbb {F}}_e \rightarrow {\mathbb {P}}^1\) be the natural projection onto the base. Then, as in [14, V, Prop. 2.3], \(\textrm{Num}({\mathbb {F}}_e) = {\mathbb {Z}}[C_e] \oplus {\mathbb {Z}}[f],\) where:
-
\(f:= \pi _e^*(p)\), for any \(p \in {\mathbb {P}}^1\), whereas
-
\(C_e\) denotes either the unique section corresponding to the morphism of vector bundles on \({\mathbb {P}}^1\)
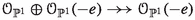 , when \(e>0\), or the fiber of the other ruling different from that induced by f, when otherwise \(e=0\).
, when \(e>0\), or the fiber of the other ruling different from that induced by f, when otherwise \(e=0\).
In particular
Let  be a rank-2 vector bundle over \({\mathbb {F}}_e\) and let
be a rank-2 vector bundle over \({\mathbb {F}}_e\) and let  be its \(i^{th}\)-Chern class. Then
be its \(i^{th}\)-Chern class. Then  , for some \( a, b \in {\mathbb {Z}}\), and
, for some \( a, b \in {\mathbb {Z}}\), and  . For the line bundle
. For the line bundle  we will also use the notation
we will also use the notation  .
.
From now on, we will consider the following:
Assumption 1.3
Let \(e \ge 0\), \(b_e\), \(k_e\) be integers such that
and let  be a rank-2 vector bundle over \({\mathbb {F}}_e\), with
be a rank-2 vector bundle over \({\mathbb {F}}_e\), with

which fits in the exact sequence

where \(A_e\) and \(B_e\) are line bundles on \({\mathbb {F}}_e\) such that
From (1.2), in particular, one has  .
.
By results in [13],  as above, turns out to be very ample on \({\mathbb {F}}_e\). Thus we take \(X_e\) to be the 3-fold scroll arising as embedding, via very-ample tautological line bundle
as above, turns out to be very ample on \({\mathbb {F}}_e\). Thus we take \(X_e\) to be the 3-fold scroll arising as embedding, via very-ample tautological line bundle  , of the projective bundle
, of the projective bundle  .
.
3 Preliminaries
In this section, for the reader convenience, we state some of the known results that we will be using in the sequel.
The following Theorem 2.1, (cf. [12, Theorem 2.4]) states under which conditions an Ulrich bundle on the base of the scroll gives rise to a bundle on the scroll itself which is Ulrich w.r.t. the tautological polarization \(\xi \).
Theorem 2.1
([12, Theorem 2.4]) Let (S, H) be a polarized surface, with H a very ample line bundle, and let  be a rank-2 vector bundle on S such that
be a rank-2 vector bundle on S such that  is (very) ample and spanned. Let
is (very) ample and spanned. Let  be a rank-\(r \ge 1\) vector bundle on S. Let
be a rank-\(r \ge 1\) vector bundle on S. Let  be a 3-fold scroll over S, where \(\xi \) is the tautological polarization, and let \(X \xrightarrow {\varphi } S\) denote the scroll map. Then the vector bundle
be a 3-fold scroll over S, where \(\xi \) is the tautological polarization, and let \(X \xrightarrow {\varphi } S\) denote the scroll map. Then the vector bundle  is Ulrich with respect to \(\xi \) if and only if the bundle
is Ulrich with respect to \(\xi \) if and only if the bundle  is such that
is such that

In particular, if  is very ample on S, then the rank-r vector bundle on X,
is very ample on S, then the rank-r vector bundle on X,  , is Ulrich with respect to \(\xi \) if and only if the rank-r vector bundle on S,
, is Ulrich with respect to \(\xi \) if and only if the rank-r vector bundle on S,  , is Ulrich with respect to
, is Ulrich with respect to  .
.
Viceversa, starting with a rank-r vector bundle on the 3-fold scroll \((X, \xi )\) which is Ulrich w.r.t. \(\xi \), satisfying suitable properties, we recall how to obtain an Ulrich vector bundle of the same rank on the base S of the scroll.
Let \(\varphi :X \rightarrow S\) be a 3-fold scroll over a surface S. Let us recall, see [5, Theorem 11.1.2.], that a general hyperplane section \({\widetilde{S}}\) of X has the structure of a blow-up of the base surface S at  points and one can consider the following diagram:
points and one can consider the following diagram:

where i is the inclusion and \(\varphi '\) is the blow-up map, where we denote by \(E_i\) the exceptional divisors of the latter map. More precisely, if \({\widetilde{S}} \in |\xi |\) is a general hyperplane section of X, then it corresponds to the vanishing locus of a general global section \({\widetilde{\sigma }} \in H^0(X, \xi )\); since one has  , then \({\widetilde{\sigma }}\) bijectively corresponds to a global section \(\sigma \) of
, then \({\widetilde{\sigma }}\) bijectively corresponds to a global section \(\sigma \) of  whose vanishing locus \(Z:= V (\sigma )\) is a zero-dimensional subscheme on S which is an element of
whose vanishing locus \(Z:= V (\sigma )\) is a zero-dimensional subscheme on S which is an element of  . From [5, Theorem 11.1.2.], \({\widetilde{S}}\) turns out to be isomorphic to the blow-up of \(\varphi ': {\widetilde{S}} \rightarrow S\) at such points Z and, for any \(z \in Z\), the \(\varphi \)-fiber \(\varphi ^{-1}(z):= F_z\) of X is contained in \({\widetilde{S}}\) as the \(\varphi '\)-exceptional divisor \(E_z\) over the point z of such a blow-up \(\varphi '\).
. From [5, Theorem 11.1.2.], \({\widetilde{S}}\) turns out to be isomorphic to the blow-up of \(\varphi ': {\widetilde{S}} \rightarrow S\) at such points Z and, for any \(z \in Z\), the \(\varphi \)-fiber \(\varphi ^{-1}(z):= F_z\) of X is contained in \({\widetilde{S}}\) as the \(\varphi '\)-exceptional divisor \(E_z\) over the point z of such a blow-up \(\varphi '\).
With this set-up, in [12, Thm. 6.1, Prop. 6.2], the authors gave conditions to get bijective correspondences among rank-r bundles on X which are Ulrich w.r.t. the tautological polarization \(\xi \) and rank-r bundles on the base surface S which are Ulrich w.r.t. the naturally related polarization as in Theorem 2.1.
Theorem 2.2
( [12, Theorem 6.1]) Let \(\varphi : X \rightarrow S\) be a 3-fold scroll over a surface S and let  be a rank-r vector bundle on X which is Ulrich with respect to the tautological polarization \(\xi \), i.e.
be a rank-r vector bundle on X which is Ulrich with respect to the tautological polarization \(\xi \), i.e.  . Let us suppose that
. Let us suppose that  is very ample on S. Assume that on the general fiber \(F=\varphi ^{-1}(s)\), \(s\in S\), the vector bundle
is very ample on S. Assume that on the general fiber \(F=\varphi ^{-1}(s)\), \(s\in S\), the vector bundle  splits as follows:
splits as follows:  . Then
. Then  , with
, with  , is a rank-r vector bundle on S which is Ulrich w.r.t.
, is a rank-r vector bundle on S which is Ulrich w.r.t.  .
.
In the following remark we comment on the hypotheses of Theorem 2.2, in order to better explain the aforementioned Ulrich-bundle bijective correspondence arising from Theorems 2.1 and 2.2 (cf. Proposition 2.4 below).
Remark 2.3
We like to point out that the assumption on the splitting-type of the vector bundle  on the general fiber F of \(\varphi \) as
on the general fiber F of \(\varphi \) as  as in Theorem 2.2 implies that such a splitting-type holds true for all \(\varphi \)-fibers \(\varphi ^{-1}(u):= F_u\), for u varying in a suitable open dense subset \(U \subseteq S\). Thus, from the previous description on the birational structure of a general hyperplane section \({\widetilde{S}} = V({\widetilde{\sigma }})\) of X as in (2.2), the main points to let the Ulrich-bundle bijective correspondence arise are first of all that the zero-dimensional scheme \(Z = V (\sigma )\), corresponding to \({\widetilde{S}} \in |\xi |\) general, is entirely contained in the open set \(U \subseteq S\) (so that, for any \(z \in Z\), the restriction of
as in Theorem 2.2 implies that such a splitting-type holds true for all \(\varphi \)-fibers \(\varphi ^{-1}(u):= F_u\), for u varying in a suitable open dense subset \(U \subseteq S\). Thus, from the previous description on the birational structure of a general hyperplane section \({\widetilde{S}} = V({\widetilde{\sigma }})\) of X as in (2.2), the main points to let the Ulrich-bundle bijective correspondence arise are first of all that the zero-dimensional scheme \(Z = V (\sigma )\), corresponding to \({\widetilde{S}} \in |\xi |\) general, is entirely contained in the open set \(U \subseteq S\) (so that, for any \(z \in Z\), the restriction of  to \(F_z:= \varphi ^{-1}(z)\) is
to \(F_z:= \varphi ^{-1}(z)\) is  namely, from (2.2),
namely, from (2.2),  , for any
, for any  , where \(\sum _i\, E_i\) denotes the total exceptional divisor of the blow-up \(\varphi '\) of S along Z) and then the use of [8, Thm. 4.2].
, where \(\sum _i\, E_i\) denotes the total exceptional divisor of the blow-up \(\varphi '\) of S along Z) and then the use of [8, Thm. 4.2].
Arguments described in Remark 2.3 are the principles used in [12] to get the following Proposition.
Proposition 2.4
([12, Prop. 6.2]) Let \(\varphi : X \rightarrow S\) be a 3-fold scroll over a surface S, where  for some very ample rank-2 vector bundle
for some very ample rank-2 vector bundle  on S. Assume that
on S. Assume that  is very ample on S. Then there exists a bijection:
is very ample on S. Then there exists a bijection:

the bijection given by the maps

and

Because we are interested on moduli spaces of Ulrich bundles on threefolds scrolls \(X_e\) over \({\mathbb {F}}_e\), as well as on moduli spaces of Ulrich bundles on \({\mathbb {F}}_e\), we recall what was already proved in [13].
Theorem 2.5
([13, Main Theorem]) For any integer \(e \ge 0\), consider the Hirzebruch surface \({\mathbb {F}}_e\) and let  denote the line bundle \(\alpha C_e + \beta f\) on \({\mathbb {F}}_e\), where \(C_e\) and f are generators of \(\textrm{Num}({\mathbb {F}}_e)\).
denote the line bundle \(\alpha C_e + \beta f\) on \({\mathbb {F}}_e\), where \(C_e\) and f are generators of \(\textrm{Num}({\mathbb {F}}_e)\).
Let \((X_e, \xi )\) be a 3-fold scroll over \({\mathbb {F}}_e\) as in Assumption 1.3, where \(\varphi : X_e \rightarrow {\mathbb {F}}_e\) denotes the scroll map. Then:
(a) \(X_e\) does not support any Ulrich line bundle w.r.t. \(\xi \) unless \(e = 0\). In this latter case, the unique Ulrich line bundles on \(X_0\) are the following:
-
(i)
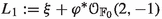 and
and 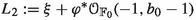 ;
; -
(ii)
for any integer \(t\ge 1\),
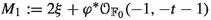 and
and 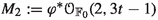 , which only occur for \(b_0=2t, k_0=3t\).
, which only occur for \(b_0=2t, k_0=3t\).
(b) Set \(e=0\) and let \(r \ge 2\) be any integer. Then the moduli space of rank-r vector bundles  on \(X_0\) which are Ulrich w.r.t. \(\xi \) and with first Chern class
on \(X_0\) which are Ulrich w.r.t. \(\xi \) and with first Chern class

is not empty and it contains a generically smooth component  of dimension
of dimension

The general point  corresponds to a slope-stable vector bundle, of slope w.r.t. \(\xi \) given by
corresponds to a slope-stable vector bundle, of slope w.r.t. \(\xi \) given by  . If moreover \(r=2\), then
. If moreover \(r=2\), then  is also special (cf. Def. 1.2 above).
is also special (cf. Def. 1.2 above).
(c) When \(e >0\), let \(r \ge 2\) be any integer. Then the moduli space of rank-r vector bundles  on \(X_e\) which are Ulrich w.r.t. \(\xi \) and with first Chern class
on \(X_e\) which are Ulrich w.r.t. \(\xi \) and with first Chern class

is not empty and it contains a generically smooth component  of dimension
of dimension

The general point  corresponds to a slope-stable vector bundle, of slope w.r.t. \(\xi \) given by
corresponds to a slope-stable vector bundle, of slope w.r.t. \(\xi \) given by  . If moreover \(r=2\), then
. If moreover \(r=2\), then  is also special.
is also special.
We want to stress that in [13, Proof of Thm. 5.1] it has been proved that bundles \(L_1, L_2\) and  , for any \(r \ge 2\), as in Theorem 2.5 split on any \(\varphi \)-fiber of \(X_e\) as requested in Theorem 2.2 and in Proposition 2.4, namely for any \(\varphi \)-fiber F, one has
, for any \(r \ge 2\), as in Theorem 2.5 split on any \(\varphi \)-fiber of \(X_e\) as requested in Theorem 2.2 and in Proposition 2.4, namely for any \(\varphi \)-fiber F, one has  whereas
whereas  (this is due to the iterative contructions in [13] of such bundles as deformations of iterative extensions). As a direct consequence of Theorem 2.5, Theorem 2.1 and the one–to–one correspondence in Proposition 2.4, in [13] we could prove the following result concerning moduli spaces of rank-r vector bundles on Hirzebruch surfaces \({\mathbb {F}}_e\), for any \(r \ge 1\) and any \(e \ge 0\), which are Ulrich w.r.t. the very ample line bundle
(this is due to the iterative contructions in [13] of such bundles as deformations of iterative extensions). As a direct consequence of Theorem 2.5, Theorem 2.1 and the one–to–one correspondence in Proposition 2.4, in [13] we could prove the following result concerning moduli spaces of rank-r vector bundles on Hirzebruch surfaces \({\mathbb {F}}_e\), for any \(r \ge 1\) and any \(e \ge 0\), which are Ulrich w.r.t. the very ample line bundle  , with \(b_e \ge 3e+2\) as it follows from Assumption 1.3 (the case \(r=1,2,3\) already known by [1, 2, 7]).
, with \(b_e \ge 3e+2\) as it follows from Assumption 1.3 (the case \(r=1,2,3\) already known by [1, 2, 7]).
Theorem 2.6
([13, Theorem 5.1]) For any integer \(e \ge 0\), consider the Hirzebruch surface \({\mathbb {F}}_e\) and let  denote the line bundle \(\alpha C_e + \beta f\) on \({\mathbb {F}}_e\), where \(C_e\) and f are generators of \(\textrm{Num}({\mathbb {F}}_e)\).
denote the line bundle \(\alpha C_e + \beta f\) on \({\mathbb {F}}_e\), where \(C_e\) and f are generators of \(\textrm{Num}({\mathbb {F}}_e)\).
Consider the very ample polarization  on \({\mathbb {F}}_e\), where \(b_e \ge 3e+2\). Then:
on \({\mathbb {F}}_e\), where \(b_e \ge 3e+2\). Then:
-
(a)
\({\mathbb {F}}_e\) does not support any Ulrich line bundle w.r.t.
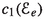 unless \(e = 0\). In this latter case, the unique line bundles on \({\mathbb {F}}_0\) which are Ulrich w.r.t.
unless \(e = 0\). In this latter case, the unique line bundles on \({\mathbb {F}}_0\) which are Ulrich w.r.t. 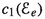 are
are 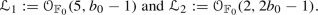
-
(b)
Set \(e=0\) and let \(r \ge 2\) be any integer. Then the moduli space
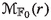 of rank-r vector bundles
of rank-r vector bundles 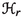 on \({\mathbb {F}}_0\) which are Ulrich w.r.t.
on \({\mathbb {F}}_0\) which are Ulrich w.r.t. 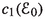 and with first Chern class
and with first Chern class 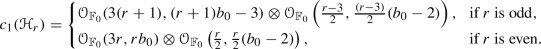
is not empty and it contains a generically smooth component of dimension
$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{(r^2 -1)}{4}(6 b_0 -4), &{} \text{ if } \text{ r } \text{ is } \text{ odd }, \\ \frac{r^2}{4} (6b_0-4) +1, &{} \text{ if } \text{ r } \text{ is } \text{ even }. \end{array}\right. } \end{aligned}$$The general point
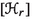 of such a component corresponds to a slope-stable vector bundle.
of such a component corresponds to a slope-stable vector bundle. -
(c)
When \(e >0\), let \(r \ge 2\) be any integer. Then the moduli space
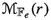 of rank-r vector bundles
of rank-r vector bundles 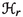 on \({\mathbb {F}}_e\) which are Ulrich w.r.t.
on \({\mathbb {F}}_e\) which are Ulrich w.r.t. 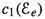 and with first Chern class
and with first Chern class 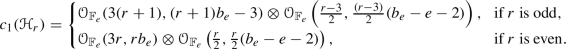
is not empty and it contains a generically smooth component of dimension
$$\begin{aligned} {\left\{ \begin{array}{ll} \left( \frac{(r -3)^2}{4}+ 2 \right) (6 b_e - 9e -4) + \frac{9}{2}(r-3) (2b_e-3e), &{} \text{ if } r \text{ is } \text{ odd }, \\ \frac{r^2}{4} (6b_e- 9e-4) +1, &{} \text{ if } r \text{ is } \text{ even }. \end{array}\right. } \end{aligned}$$The general point
 of such a component corresponds to a slope-stable vector bundle.
of such a component corresponds to a slope-stable vector bundle.
4 Moduli spaces
Our aim in this section is to prove that the moduli space  of Ulrich bundles on \({\mathbb {F}}_e\), \(e \ge 0\), as in Theorem 2.6 is irreducible, generically smooth and unirational, whereas that the generically smooth modular component
of Ulrich bundles on \({\mathbb {F}}_e\), \(e \ge 0\), as in Theorem 2.6 is irreducible, generically smooth and unirational, whereas that the generically smooth modular component  of Ulrich bundles on \(X_e\), \(e \ge 0\), as in Theorem 2.5 is unirational.
of Ulrich bundles on \(X_e\), \(e \ge 0\), as in Theorem 2.5 is unirational.
Theorem 3.1
Let  be the moduli space of rank-r vector bundles
be the moduli space of rank-r vector bundles  on \({\mathbb {F}}_e\) which are Ulrich w.r.t.
on \({\mathbb {F}}_e\) which are Ulrich w.r.t.  and with first Chern class
and with first Chern class

(see Theorem 2.6). Then  is generically smooth, irreducible, unirational and of dimension
is generically smooth, irreducible, unirational and of dimension

Proof
From Theorem 2.6 we know that the moduli space  is not empty.
is not empty.
Let  be any irreducible component and let
be any irreducible component and let  be its general point. So
be its general point. So  is of rank r and as in the statement of Theorem 3.1.
is of rank r and as in the statement of Theorem 3.1.
For simplicity let  . By [1, Theorem 1.1]
. By [1, Theorem 1.1]  necessarily fits into the following short exact sequence
necessarily fits into the following short exact sequence

where \(\gamma =\alpha +\beta -r(2+b_e)-e(\alpha -3r)\), \(\delta =\beta -r(b_e-1)-e(\alpha -3r)\), \(\tau =\alpha -2r\) which, after plugging in the value of \(\alpha \) and \(\beta \), become
\(\gamma =\frac{(b_e-2e+1)r-b_e+3}{2}\), \(\delta = \frac{(r-1)b_e}{2}-er\), \(\tau =\frac{3(r+1)}{2}\), if r is odd, and
\(\gamma = \frac{(b_e-2e+1)r}{2}\), \(\delta = \frac{(b_e-2e)r}{2}\), \(\tau =\frac{3r}{2}\), if r is even.
Thus  is expressed as the cokernel of an injective map \(\phi \in \textrm{Hom}_{{\mathbb {F}}_e} ( {\mathscr {A}}, {\mathscr {B}})\), where
is expressed as the cokernel of an injective map \(\phi \in \textrm{Hom}_{{\mathbb {F}}_e} ( {\mathscr {A}}, {\mathscr {B}})\), where  and
and  , with \(\gamma , \delta , \tau \) as above.
, with \(\gamma , \delta , \tau \) as above.
On the other hand, by [1, Theorem 1.3], if we take a general map \(\phi _{gen} \in \textrm{Hom}_{{\mathbb {F}}_e} ( {\mathscr {A}}, {\mathscr {B}})\) then \(\textrm{coker}(\phi _{gen})\) is a rank-r vector bundle on \({\mathbb {F}}_e\), in particular locally free, which is Ulrich w.r.t.  , and with Chern classes \(c_1(\textrm{coker}(\phi _{gen}))\) and \(c_2(\textrm{coker}(\phi _{gen}))\) as those of
, and with Chern classes \(c_1(\textrm{coker}(\phi _{gen}))\) and \(c_2(\textrm{coker}(\phi _{gen}))\) as those of  . Since \( {\mathscr {A}}, {\mathscr {B}}\) are uniquely determined by r, e, \((3,b_e)\) and
. Since \( {\mathscr {A}}, {\mathscr {B}}\) are uniquely determined by r, e, \((3,b_e)\) and  and since \(\textrm{Hom}_{{\mathbb {F}}_e} ( {\mathscr {A}}, {\mathscr {B}})\) is irreducible, it follows that
and since \(\textrm{Hom}_{{\mathbb {F}}_e} ( {\mathscr {A}}, {\mathscr {B}})\) is irreducible, it follows that  , i.e.
, i.e.  is therefore irreducible and moreover it is unirational, being dominated by \(\textrm{Hom}_{{\mathbb {F}}_e} ( {\mathscr {A}}, {\mathscr {B}})\).
is therefore irreducible and moreover it is unirational, being dominated by \(\textrm{Hom}_{{\mathbb {F}}_e} ( {\mathscr {A}}, {\mathscr {B}})\).
The generic smoothness of  and the formula for its dimension follow as they have already been proved in Theorem 2.6-(b), (c). \(\square \)
and the formula for its dimension follow as they have already been proved in Theorem 2.6-(b), (c). \(\square \)
Theorem 3.2
For any integer \(e \ge 0\), let \({\mathbb {F}}_e\) be the Hirzebruch surface and let  denote the line bundle \(\alpha C_e + \beta f\) on \({\mathbb {F}}_e\), where \(C_e\) and f are generators of \(\textrm{Num}({\mathbb {F}}_e)\).
denote the line bundle \(\alpha C_e + \beta f\) on \({\mathbb {F}}_e\), where \(C_e\) and f are generators of \(\textrm{Num}({\mathbb {F}}_e)\).
Let \((X_e, \xi )\) be a 3-fold scroll over \({\mathbb {F}}_e\) as in Assumption 1.3, where \(\varphi : X_e \rightarrow {\mathbb {F}}_e\) denotes the scroll map. Then the moduli space of rank-\(r\ge 2\) vector bundles  on \(X_e\) which are Ulrich w.r.t. \(\xi \) and with first Chern class as in Theorem 2.5 is not empty and it contains a generically smooth component
on \(X_e\) which are Ulrich w.r.t. \(\xi \) and with first Chern class as in Theorem 2.5 is not empty and it contains a generically smooth component  which is unirational and of dimension
which is unirational and of dimension

Proof
As we have seen in the proof of Theorem 3.1, a general  , turns out to be
, turns out to be  , with \(\phi \) a general vector bundle morphism as in (3.1).
, with \(\phi \) a general vector bundle morphism as in (3.1).
Now take  ,
,  , \(\gamma , \delta \) and \(\tau \) as in the proof of Theorem 3.1; then for \(\phi \in \textrm{Hom}_{{\mathbb {F}}_e} ( {\mathscr {A}}, {\mathscr {B}})\) general, one has therefore
, \(\gamma , \delta \) and \(\tau \) as in the proof of Theorem 3.1; then for \(\phi \in \textrm{Hom}_{{\mathbb {F}}_e} ( {\mathscr {A}}, {\mathscr {B}})\) general, one has therefore

We first tensor this exact sequence by  , then we pull it back via \(\varphi ^*\), where \(\varphi : X_e \rightarrow {\mathbb {F}}_e\) is the scroll map, and the sequence remains exact on the left since
, then we pull it back via \(\varphi ^*\), where \(\varphi : X_e \rightarrow {\mathbb {F}}_e\) is the scroll map, and the sequence remains exact on the left since  is locally free; subsequently we tensor the resulting short exact sequence with \(\xi \), the tautological polarization on \(X_e\), and thus we get the exact sequence
is locally free; subsequently we tensor the resulting short exact sequence with \(\xi \), the tautological polarization on \(X_e\), and thus we get the exact sequence

defining \({\overline{\phi }}\). Set  and
and  . Recall that the modular component \({\mathcal {M}}(r)\) as in Theorem 2.5 has an open dense subset parametrizing isomorphism classes of slope-stable, rank-r vector bundles
. Recall that the modular component \({\mathcal {M}}(r)\) as in Theorem 2.5 has an open dense subset parametrizing isomorphism classes of slope-stable, rank-r vector bundles  , which are Ulrich w.r.t. the tautological polarization \(\xi \) of \(X_e\) and with Chern classes determined by the iterative constructions as in [13] (in particular, the first Chern class \(c_1\) is as reminded in Theorem 2.5); for
, which are Ulrich w.r.t. the tautological polarization \(\xi \) of \(X_e\) and with Chern classes determined by the iterative constructions as in [13] (in particular, the first Chern class \(c_1\) is as reminded in Theorem 2.5); for  general it has also been proved in [13, Proof of Thm. 5.1] that the bundle
general it has also been proved in [13, Proof of Thm. 5.1] that the bundle  has in particular the splitting type requested by Proposition 2.4, namely
has in particular the splitting type requested by Proposition 2.4, namely  , on any \(\varphi \)-fiber F. As a consequence of the bijective correspondence induced by Proposition 2.4, in [13] we deduced therefore that
, on any \(\varphi \)-fiber F. As a consequence of the bijective correspondence induced by Proposition 2.4, in [13] we deduced therefore that  , with
, with  Ulrich w.r.t.
Ulrich w.r.t.  on \({\mathbb {F}}_e\) as above.
on \({\mathbb {F}}_e\) as above.
Then the sequence (3.2) reads

In particular, for those morphisms \({\overline{\phi }} \in \textrm{Hom}_{X_e} ( {\overline{{\mathscr {A}}}}, {\overline{{\mathscr {B}}}})\) such that  , one has that \(\textrm{coker}({\overline{\phi }}) \) is locally free, of rank r and it is moreover Ulrich on \(X_e\) w.r.t. the tautological polarization \(\xi \), with Chern classes
, one has that \(\textrm{coker}({\overline{\phi }}) \) is locally free, of rank r and it is moreover Ulrich on \(X_e\) w.r.t. the tautological polarization \(\xi \), with Chern classes  , \(1 \le i \le 3\), computed by iterative constructions of the vector bundles
, \(1 \le i \le 3\), computed by iterative constructions of the vector bundles  as in [13] (e.g. \(c_1\) is reminded in Theorem 2.5 above).
as in [13] (e.g. \(c_1\) is reminded in Theorem 2.5 above).
Let \({{\overline{\phi }}_{gen}} \in \textrm{Hom}_{X_e} ({\overline{{\mathscr {A}}}},{\overline{{\mathscr {B}}}})\) be general; since

i.e. \({\mathscr {A}}^{\vee }\otimes {\mathscr {B}}\) is globally generated, so \({\overline{{\mathscr {A}}}}^{\vee } \otimes {\overline{{\mathscr {B}}}}\) is also globally generated. Therefore, by [3, Thm. 4.2], (cf. also [4, Thm. 2]) \({{\overline{\phi }}_{gen}}\) is injective and it gives rise to an exact sequence

Since \({\overline{\phi }} \in \textrm{Hom}_{X_e} ( {\overline{{\mathscr {A}}}}, {\overline{{\mathscr {B}}}})\) as in (3.3) is such that  is locally free, then also \(\textrm{coker}({{\overline{\phi }}_{gen}})\) is locally free, as locally freeness is an open condition on the (irreducible) vector space \( \textrm{Hom}_{X_e} ( {\overline{{\mathscr {A}}}}, {\overline{{\mathscr {B}}}})\). Moreover, the rank of \(\textrm{coker}({{\overline{\phi }}_{gen}})\) is given by
is locally free, then also \(\textrm{coker}({{\overline{\phi }}_{gen}})\) is locally free, as locally freeness is an open condition on the (irreducible) vector space \( \textrm{Hom}_{X_e} ( {\overline{{\mathscr {A}}}}, {\overline{{\mathscr {B}}}})\). Moreover, the rank of \(\textrm{coker}({{\overline{\phi }}_{gen}})\) is given by  , with \(\gamma , \delta , \tau \) as in the proof of Theorem 3.1. Furthermore, once again from the irreducibility of \(\textrm{Hom}_{X_e} ({\overline{{\mathscr {A}}}},{\overline{{\mathscr {B}}}})\) and from the constancy of Chern classes in irreducible flat families of vector bundles of given rank (or even from the fact that
, with \(\gamma , \delta , \tau \) as in the proof of Theorem 3.1. Furthermore, once again from the irreducibility of \(\textrm{Hom}_{X_e} ({\overline{{\mathscr {A}}}},{\overline{{\mathscr {B}}}})\) and from the constancy of Chern classes in irreducible flat families of vector bundles of given rank (or even from the fact that  and \(\textrm{coker}({{\overline{\phi }}_{gen}})\) are both locally free cokernels of injective vector bundle morphisms in \(\textrm{Hom}_{X_e} ( {\overline{{\mathscr {A}}}}, {\overline{{\mathscr {B}}}})\)) one has that
and \(\textrm{coker}({{\overline{\phi }}_{gen}})\) are both locally free cokernels of injective vector bundle morphisms in \(\textrm{Hom}_{X_e} ( {\overline{{\mathscr {A}}}}, {\overline{{\mathscr {B}}}})\)) one has that

Finally since  is Ulrich on \(X_e\) w.r.t. \(\xi \) we have
is Ulrich on \(X_e\) w.r.t. \(\xi \) we have

then by semicontinuity
hence \(\textrm{coker}({{\overline{\phi }}}_{gen})\) is Ulrich w.r.t. \(\xi \).
The fact that \(\textrm{Hom}_{X_e} ({\overline{{\mathscr {A}}}},{\overline{{\mathscr {B}}}})\) is irreducible implies that it must dominate the modular component  (as in Theorem 2.5) containing
(as in Theorem 2.5) containing  as its general point, which therefore implies that
as its general point, which therefore implies that  is unirational. The generic smoothness of
is unirational. The generic smoothness of  as well as its dimension formula have already being proved in Theorem 2.5-(b), (c) (more precisely in [13, Main Theorem]). \(\square \)
as well as its dimension formula have already being proved in Theorem 2.5-(b), (c) (more precisely in [13, Main Theorem]). \(\square \)
References
Antonelli, V.: Characterization of Ulrich bundles on Hirzebruch surfaces. Revista Matemàtica Complutense 34, 43–74 (2021). https://doi.org/10.1007/s13163-019-00346-7
Aprodu, M., Costa, L., Miró-Roig, R.M.: Ulrich bundles on ruled surfaces. J. Pure Appl. Algebra 222(1), 131–138 (2018)
Bănică, C.: Smooth reflexive sheaves. In: Proceedings of the Colloquium on Complex Analysis and the Sixth Romanian-Finnish Seminar, vol. 36, pp. 571–593 (1991)
Bănică, C.: Faisceaux réflexifs lisses. C. R. Acad. Sci. Paris, t. 31, Série I 253–255 (1990)
Beltrametti, M., Sommese, A.J.: The Adjunction Theory of Complex Projective Varieties, vol. 16 of Expositions in Mathematics. De Gruyter (1995)
Casanellas, M., Hartshorne, R., Geiss, F., Schreyer, F.-O.: Stable Ulrich bundles. Int. J. Math. 23(8), 1250083 (2012)
Casnati, G.: Special Ulrich bundles on non-special surfaces with \(p_g = q = 0\). Int. J. Math. 28(8), 1750061 (2017)
Casnati, G., Kim, Y.: Ulrich bundles on blowing up (and an erratum). C. R. Acad. Sci. Paris Ser. I 355(3), 1291–1297 (2017)
Costa, L., Miró-Roig, R.M.: Rationality of moduli spaces of vector bundles on rational surfaces. Nagoya Math. J. 165, 43–69 (2002)
Costa, L., Miró–Roig, R.M., Pons–Llopis, J.: Ulrich bundles from commutative algebra to algebraic geometry. Stud. Math. 77 (2021) De Gruyter
Faenzi, D., Pons-Llopis, J.: The Cohen–Macaulay representation type of projective arithmetically Cohen-Macaulay varieties. Epijournal de Géometrie Algébrique 5(8), 1–37 (2021)
Fania, M.L., Lelli-Chiesa, M., Pons Llopis, J.: Ulrich bundles on three-dimensional scrolls. Int. Math. Res. Not. 2021(17), 13478–13507 (2019). https://doi.org/10.1093/imrn/rnz288
Fania, M.L., Flamini, F.: Ulrich bundles on some threefold scrolls over \({\mathbb{F} }_e\). Adv. Math. 436, 109409 (2024). https://doi.org/10.1016/j.aim.2023.109409
Hartshorne, R.: Algebraic Geometry. In: Number 52 in GTM. Springer, New York, Heidelberg (1977)
Acknowledgements
The first author has been supported by PRIN 2017SSNZAW. The second author has been partially supported by the MIUR Excellence Department Project MatMod@TOV MIUR CUP-E83C23000330006, 2023–2027, awarded to the Department of Mathematics, University of Rome Tor Vergata. Both authors are members of INdAM-GNSAGA. The authors would like to thank M. Aprodu, since this article came about as a result of some of his questions posed during the conference “Algebraic Geometry in L’Aquila”, July 18–21, 2023, regarding possible irreducibility of the moduli spaces studied in [13]. Finally, the authors would like to thank the anonymous Referee for his/her advices, questions and remarks which have also improved the presentation of the present paper.
Funding
Open access funding provided by Università degli Studi dell’Aquila within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
To Enrique Arrondo, in the occasion of his 60th birthday.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fania, M.L., Flamini, F. A note on some moduli spaces of Ulrich bundles. Rend. Circ. Mat. Palermo, II. Ser (2024). https://doi.org/10.1007/s12215-024-01068-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12215-024-01068-6



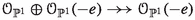 , when
, when 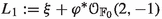 and
and 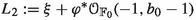 ;
;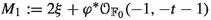 and
and 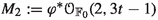 , which only occur for
, which only occur for 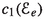 unless
unless 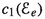 are
are 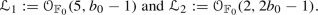
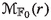 of rank-r vector bundles
of rank-r vector bundles 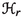 on
on 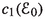 and with first Chern class
and with first Chern class 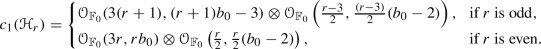
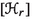 of such a component corresponds to a slope-stable vector bundle.
of such a component corresponds to a slope-stable vector bundle.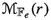 of rank-r vector bundles
of rank-r vector bundles 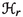 on
on 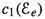 and with first Chern class
and with first Chern class 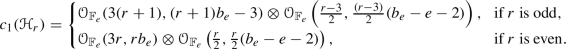
 of such a component corresponds to a slope-stable vector bundle.
of such a component corresponds to a slope-stable vector bundle.