Skip to main content
SpringerLink
Log in

Reliability optimization of cutting parameters considering the diameter error of slender shaft

  • Original Article
  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

Abstract

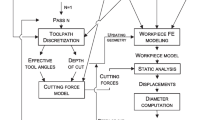
In slender shaft turning, any diameter error in the workpieces can cause cutting tool wear and poor machining accuracy. Published research ignores the integrated analysis of diameter error, the randomness of parameters, and optimization models. This paper sets material removal rate (MRR) as the optimization objective function and considers the randomness of cutting parameters in a reliability parameter optimization model design, under the constraint of diameter error. The cutting force is calculated based on the unequal shear zone model and is used in finite element analysis of the slender shaft, deriving the diameter error model. The derived complex error model is replaced by the Kriging fitting method, reducing the calculation time to less than 1 %. Single loop sequence optimization and reliability assessment (SORA) is used to optimize reliability. The results show significant improvement of the MRR, while the reliability of each constraint condition is close to 1.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. P. Huang, W. B. Lee and C. Y. Chan, Investigation of the effects of spindle unbalance induced error motion on machining accuracy in ultra-precision diamond turning, International Journal of Machine Tools and Manufacture, 94 (2015) 48–56.

    Article  Google Scholar 

  2. Z. Kejia, W. Jian, Z. Dahu and D. Han, Analytical modeling and experimental validation of cutting forces considering edge effects and size effects with round chamfered ceramic tools, Journal of Manufacturing Science and Engineering, 140(8) (2018) 081012.

    Article  Google Scholar 

  3. Y. Gao, R. Sun and J. Leopold, An analytical force model for modulation-assisted turning, Journal of Manufacturing Processes, 31 (2018) 712–730.

    Article  Google Scholar 

  4. L. Carrino, G. Giorleo and W. Polini, Dimensional errors in longitudinal turning based on the unified generalized mechanics of cutting approach, International Journal of Machine Tools and Manufacture, 42(14) (2002) 1517–1525.

    Article  Google Scholar 

  5. W. Wei, C. Li, Y. X. Zhou, H. Wang and Y. M. Zhang, Nonlinear dynamic analysis for machine tool table system mounted on linear guides, Nonlinear Dynamics, 94(3) (2018) 2033–2045.

    Article  Google Scholar 

  6. L. Z. Qiang, Finite difference calculations of the deformations of multi-diameter workpieces during turning, Journal of Materials Processing Technology, 98(3) (2000) 310–316.

    Article  Google Scholar 

  7. G. Cloutier, R. Mayer and A. V. Phan, Singularity function representation in obtaining closed-form solutions to workpiece deflections in turning multi-diameter bars, Computer Modeling and Simulation in Engineering, 4(2) (1999) 133–137.

    Google Scholar 

  8. A. M. Nalbant, H. Gokkaya and G. Sur, Application of Taguchi method in the optimization of cutting parameters for surface roughness in turning, Materials and Design, 28(4) (2007) 1379–1385.

    Article  Google Scholar 

  9. S. A. Krishnan and G. L. Samuel, Multi-objective optimization of material removal rate and surface roughness in wire electrical discharge turning, International Journal of Advanced Manufacturing Technology, 67(9–12) (2013) 2021–2032.

    Article  Google Scholar 

  10. B. Li, X. Wang, Y. Hu and C. Li, Analytical prediction of cutting forces in orthogonal cutting using unequal division shear-zone model, International Journal of Advanced Manufacturing Technology, 54(5–8) (2011) 431–443.

    Article  Google Scholar 

  11. G. Jianliang and H. Rongdi, A united model of diametral error in slender bar turning with a follower rest, International Journal of Machine Tools and Manufacture, 46(9) (2006) 1002–1012.

    Article  Google Scholar 

  12. V. P. Astakhov, M. O. M. Osman and M. T. Hayajneh, Reevaluation of the basic mechanics of orthogonal metal cutting: velocity diagram, virtual work equation and upper-bound theorem, International Journal of Machine Tools and Manufacture, 41(3) (2001) 393–418.

    Article  Google Scholar 

  13. N. Tounsi, J. Vincenti, A. Otho and M. A. Elbestawi, From the basics of orthogonal metal cutting toward the indentification of the constitutive equation, International Journal of Machine Tools and Manufacturing, 42(2) (2002) 1373–1383.

    Article  Google Scholar 

  14. D. Dudzinski and A. Molinari, A modelling of cutting for viscoplastic materials, International Journal of Mechanical Sciences, 39(4) (1997) 369–389.

    Article  Google Scholar 

  15. A. Moufki, A. Devillez, D. Dudzinski and A. Molinari, Thermomechanical modelling of oblique cutting and experimental validation, International Journal of Machine Tools and Manufacture, 44(9) (2004) 971–989.

    Article  Google Scholar 

  16. N. C. Tounsi, J. Vincenti and A. Otho, From the basic mechanics of orthogonal metal cutting toward the identification of the constitutive equation, International Journal of Machine Tools and Manufacture, 42(12) (2002) 1373–1383.

    Article  Google Scholar 

  17. N. Fang, A quantitative sensitivity analysis of cutting performances in orthogonal machining with restricted contact and flat-faced tools, Journal of Manufacturing Science and Engineering, 126(2) (2004) 408–411.

    Article  Google Scholar 

  18. J. R. R. Mayer, A. V. Phan and G. Cloutier, Prediction of diameter errors in bar turning: a computationally effective model, Applied Mathematical Modelling, 24(12) (2000) 943–956.

    Article  Google Scholar 

  19. A. V. Phan, G. Cloutier and J. R. R. Mayer, A finite-element model with closed-form solutions to workpiece deflections in turning, International Journal of Production Research, 37(17) (1999) 4039–4051.

    Article  Google Scholar 

  20. X. Z. Huang, F. J. Jia, Y. M. Zhang and J. H. Lian, Prediction of surface location error in milling considering the effects of uncertain factors, Mechanical Sciences, 8(2) (2017) 385–392.

    Article  Google Scholar 

  21. D. Sambakhé, L. Rouan, J. N. Bacro and E. Gozé, Conditional optimization of a noisy function using a Kriging metamodel, Journal of Global Optimization, 73(3) (2019) 615–636.

    Article  MathSciNet  Google Scholar 

  22. Z. Sun, J. Wang, R. I. Li and C. I. Tong, LIF: a new Kriging based learning function and its application to structural reliability analysis, Reliability Engineering and System Safety, 157 (2017) 152–165.

    Article  Google Scholar 

  23. T. Simpson, F. Mistree, J. Korte and F. Misstree, Comparison of response surface and Kriging models for multidisciplinary design optimization, Symposium on Multidisciplinary Analysis and Optimization, 1998 (1998) 4755.

    Google Scholar 

  24. S. H. Kim and S. W. Na, Response surface method using vector projected sampling points, Structural Safety, 19(1) (1997) 3–19.

    Article  Google Scholar 

  25. Y. Gao, L. S. Turng and X. Wang, Adaptive geometry and process optimization for injection molding using the Kriging surrogate model trained by numerical simulation, Advances in Polymer Technology, 27(1) (2010) 1–16.

    Article  Google Scholar 

  26. A. Olsson, G. Sandberg and O. Dahlblom, On latin hypercube sampling for structural reliability analysis, Structural Safety, 25(1) (2003) 47–68.

    Article  Google Scholar 

  27. X. Du, Saddlepoint approximation for sequential optimization and reliability analysis, Journal of Mechanical Design, 130(1) (2008) 842–849.

    Article  Google Scholar 

  28. X. Z. Huang, M. W. Hu and Y. M. Zhang, An approach for optimization of turning parameters considering uncertainty parameters, The International Journal of Advanced Manufacturing Technology, 93 (2017) 3339–3346.

    Article  Google Scholar 

Download references

Acknowledgments

This research is supported by the National Natural Science Foundation of China (51975110), the Liaoning Revitalization Talents Program (XLYC1907171), and Fundamental Research Funds for the Central Universities (N2003005).

Author information

Authors and Affiliations

  1. School of Mechanical Engineering and Automation, Northeastern University, Shenyang, 110819, China

    Pengfei Ding, Xianzhen Huang, Yuxiong Li & Guodong Yang

  2. Key Laboratory of Vibration and Control of Aero-Propulsion Systems Ministry of Education of China, Northeastern University, Shenyang, 110819, China

    Xianzhen Huang

  3. CRRC Qingdao Sifang Rolling Stock Res Inst COLTD, Qingdao, 266031, China

    Guodong Yang

Authors
  1. Pengfei Ding
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xianzhen Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yuxiong Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Guodong Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xianzhen Huang.

Additional information

Pengfei Ding received the M.S. degree from School of Mechanical Engineering and Automation in Northeast University in 2020, where he is currently pursuing the Ph.D. degree. His main interests include mechanical reliability design and analysis of machine tool cutting stability.

Xianzhen Huang received the M.S. degree and Ph.D. degree from School of Mechanical Engineering and Automation in Northeast University. He conducted scientific research as a visiting student with the Durham University in 2018. He is currently a Professor and also the Deputy Director of the Research Center for Mechanical Reliability and Dynamics with Northeast University. He was selected in new century talent supporting project by Ministry of Education in China and was awarded the First Prize in Liaoning Province Science and Technology Award. His research interests include design under uncertainty, machine tool dynamics and metamodeling.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ding, P., Huang, X., Li, Y. et al. Reliability optimization of cutting parameters considering the diameter error of slender shaft. J Mech Sci Technol 35, 4673–4683 (2021). https://doi.org/10.1007/s12206-021-0934-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12206-021-0934-0

Keywords

Search

Navigation