Skip to main content
SpringerLink
Log in

A non-iterative implicit integration method using a HHT-α integrator for real-time analysis of multibody systems

  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

Abstract

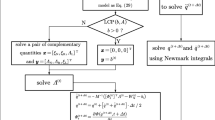
This paper proposes a non-iterative implicit integration method for real-time analysis of multibody systems. Although the implicit Euler integrator is widely used for real-time simulations, we use a HHT-α integrator to improve the accuracy of the solution. For a noniterative procedure, the HHT-α integral formula was reformed and applied to the linearized equations of motion for multibody systems. A stability analysis of the HHT-α integrator was carried out to determine whether the proposed integrator has absolute stability. Numerical simulations with stiff linear systems that represent a highly damped system and a highly oscillatory system were also carried out to evaluate the performance of the proposed integrator. For non-linear multibody systems, the performance of the proposed integrator was also evaluated with a double pendulum example. Through the double pendulum multibody simulations, we confirmed the accuracy and stability characteristics of the proposed integration method by comparison of the conventional HHT-α integrator with the iterative method and the implicit Euler integrator, which is widely used in real-time applications.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. A. Cardona and M. Geradin, Time integration of the equations of motion in mechanism analysis, Computers & Structures, 33 (3) (1989) 801–820.

    Article  MATH  Google Scholar 

  2. E. J. Haug, D. Negrut and M. Iancu, A state-space-based implicit integration algorithm for differential-algebraic equations of multibody dynamics, Journal of Structural Mechanics, 25 (3) (1997) 311–334.

    MathSciNet  Google Scholar 

  3. D. Negrut, R. Rampalli, G. Ottarsson and A. Sajdak, On an implementation of the Hilber-Hughes-Taylor method in the context of index 3 differential-algebraic equations of multibody dynamics (DETC2005–85096), Journal of Computational and Nonlinear Dynamics, 2 (1) (2007) 73–85.

    Article  Google Scholar 

  4. D. Negrut, L. O. Jay and N. Khude, A discussion of loworder numerical integration formulas for rigid and flexible multibody dynamics, Journal of Computational and Nonlinear Dynamics, 4 (2) (2009) 021008.

    Article  Google Scholar 

  5. J. Wang and Z. Li, Implementation of HHT algorithm for numerical integration of multibody dynamics with holonomic constraints, Nonlinear Dynamics, 80 (1–2) (2015) 871–825.

    MathSciNet  Google Scholar 

  6. N. M. Newmark, A method of computation for structural dynamics, Journal of the Engineering Mechanics Division, 85 (3) (1959) 67–94.

    Google Scholar 

  7. H. M. Hilber, T. J. Hughes and R. L. Taylor, Improved numerical dissipation for time integration algorithms in structural dynamics, Earthquake Engineering & Structural Dynamics, 5 (3) (1977) 283–292.

    Article  Google Scholar 

  8. G. Rill, A modified implicit Euler algorithm for solving vehicle dynamics equations, Multibody System Dynamics, 15 (1) (2006) 1–24.

    Article  MATH  Google Scholar 

  9. B. Burgermeister, M. Arnold and B. Esterl, DAE time integration for real-time applications in multi-body dynamics, ZAMM-Journal of Applied Mathematics and Mechanics, 86 (10) (2006) 759–771.

    Article  MathSciNet  MATH  Google Scholar 

  10. M. Arnold, B. Burgermeister and A. Eichberge, Linearly implicit time integration methods in real-time applications: DAEs and stiff ODEs, Multibody System Dynamics, 17 (2–3) (2007) 99–117.

    Article  MathSciNet  MATH  Google Scholar 

  11. M. Carpinelli, M. Gubitosa, D. Mundo and W. Desmet, Automated independent coordinates’ switching for the solution of stiff DAEs with the linearly implicit Euler method, Multibody System Dynamics, 36 (1) (2016) 67–85.

    Article  MathSciNet  MATH  Google Scholar 

  12. M. Nakashima, Integration techniques for substructure pseudo-dynamic test, Proceedings of 4th U.S. National Conference on Earthquake Engineering, Palm Springs, California, USA (1990) 515–524.

    Google Scholar 

  13. D. Combescure and P. Pegon, a-Operator splitting time integration technique for pseudodynamic testing error propagation analysis, Soil Dynamics and Earthquake Engineering, 16 (7–8) (1997) 427–443.

    Article  Google Scholar 

  14. A. Cunha, E. Caetano and P. Ribeiro, Non-iterative integration methods with desired numerical dissipation, Eurodyn 2014, Proceedings of the 9th International Conference on Structure Dynamics, Porto, Portugal (2014) 1819–1826.

    Google Scholar 

  15. K. E. Atkinson, An Introduction to Numerical Analysis, John Wiley & Sons, New York, USA (1978).

    MATH  Google Scholar 

  16. C. W. Gear, Numerical Initial Value Problems in Ordinary Differential Equations, Prentice-Hall PTR, Englewood Cliffs, USA (1971).

    Google Scholar 

  17. E. J. Haug, Computer Aided Kinematics and Dynamics of Mechanical Systems, Allyn and Bacon, Boston, USA (1989).

    Google Scholar 

  18. E. J. Haug, Intermediate Dynamics, Prentice Hall, Englewood Cliffs, USA (1992).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechatronics Engineering, Chungnam National University, #99, Daehak-ro, Yuseong-gu, Daejeon, 34134, Korea

    Myoungho Kim & Sung-Soo Kim

  2. Intelligent Robotics Research Center, Korea Electronics Technology Institute, #655, Pyeongcheon-ro, Wonmi-gu, Bucheon-si, Gyeonggi-do, 14502, Korea

    Hajun Song

Authors
  1. Myoungho Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hajun Song
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sung-Soo Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sung-Soo Kim.

Additional information

Recommended by Associate Editor Kyoung-Su Park

Myoungho Kim received his master’s degree in Mechatronics Engineering from Chungnam National University, Korea at 2013. He is currently studying Ph.D. at the Department of Mechatronics Engineering, Chungnam National University and the Korea Atomic Energy Research Institute. His research interests are multibody dynamics and control for robot systems.

Hajun Song graduated from the Dept. of Mechatronics Engineering at Chungnam National University, Korea in 2015. He received his master’s degree in Mechatronics Engineering from Chungnam National University in 2018. His research interests are real-time applications of multibody dynamics and modeling.

Sung-Soo Kim received his Ph.D. degree in Mechanical Engineering from University of Iowa, U.S.A., in 1988. He is currently a Professor of the Mechatronics Engineering Department at Chungnam National University, Daejeon, Korea. His research interests are real-time multibody dynamics and its application to automotive systems and robot systems.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kim, M., Song, H. & Kim, SS. A non-iterative implicit integration method using a HHT-α integrator for real-time analysis of multibody systems. J Mech Sci Technol 33, 1087–1096 (2019). https://doi.org/10.1007/s12206-019-0208-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12206-019-0208-2

Keywords

Search

Navigation