Skip to main content
SpringerLink
Log in

Critical speed of high-speed trains considering wheel-rail contact

  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

Abstract

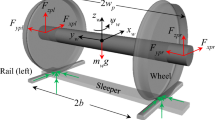
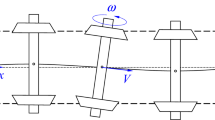
The maximum speed of a high-speed train is limited to its critical speed. In this study, the definition of critical speed is reviewed. The relationship between creepage and creep force and the effects of the parameters of the first and second suspension systems are also studied using a bogie model to increase the critical speed. Kalker’s linear creep theory and its modification of Wormey’s saturation constant are reviewed. The nonlinear creep force of Vermeulen’s creep theory, Polach’s calculation, and the newly calculated longitudinal and lateral creep forces using strip theory from wheel-rail contact pressure are investigated for the critical speed. Flange contact is also considered when lateral displacement exceeds the dead band between wheel flange and rail. Direct numerical integration and a shooting algorithm are devised to calculate the response, especially for the limit cycle. Results show that as speed increases, the equilibrium point becomes unstable and creates a limit cycle through a Hopf bifurcation. The unstable fixed point can be a critical speed. The critical speed increases as the creep curve becomes stiff before saturation, which is more effective than the variation in suspension parameters. The consideration of flange contact can also increase the critical speed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. N. K. Cooperrider, The hunting behavior of conventional railway trucks, Journal of Manufacturing Science and Engineering, 94 (2) (1972) 752–762.

    Google Scholar 

  2. R. R. Huilgol, Hopf-Friedrichs bifurcation and the hunting of a railway axle, Quarterly PMM Journal of Applied Mathematics and Mechanics, 12 (1978) 85–94.

    MathSciNet  Google Scholar 

  3. M. Ahmadian and S. Yang, Hopf bifurcation and hunting behavior in a rail wheelset with flange contact, Nonlinear Dynamics, 15 (1998) 15–30.

    Article  MATH  Google Scholar 

  4. J. Zeng, W. H. Zhang, H. Y. Dai, X. J. Wu and Z. Y. Shen, Hunting instability analysis and H8 controlled stabilizer design for high speed railway passenger car, International Journal of Vehicle Mechanics and Mobility, 29 (1) (1998) 655–668.

    Google Scholar 

  5. W. Chung and S. Kim, A study on the critical speed of railway vehicles, Transaction of KSME A, 24 (8) (2000) 1991–1999.

    MathSciNet  Google Scholar 

  6. P. Kim and J. Seok, Bifurcation analysis on the hunting behavior of a dual-bogie railway vehicle using the method of multiple scales, Journal of Sound and Vibration, 329 (2010) 4017–4039.

    Article  Google Scholar 

  7. S. Y. Lee and Y. C. Cheng, Hunting stability analysis of high-speed railway vehicle trucks on tangent tracks, Journal of Sound and Vibration, 282 (2005) 881–898.

    Article  Google Scholar 

  8. Y. C. Cheng, S. Y. Lee and H. H. Chen, Modeling and nonlinear hunting stability analysis of high-speed railway vehicle moving on curved tracks, Journal of Sound and Vibration, 24 (3) (2009) 139–160.

    Article  MathSciNet  MATH  Google Scholar 

  9. S. Y. Lee and Y. C. Cheng, Nonlinear analysis on the hunting stability of high speed railway vehicle trucks on curved tracks, Journal of Vibration and Acoustics, 127 (2005) 324–332.

    Article  Google Scholar 

  10. J. Park, H. Koh and N. Kim, Parametric study of lateral stability for a railway vehicle, Journal of Mechanical Science and Technology, 25 (7) (2011) 1657–1666.

    Article  Google Scholar 

  11. D. Bigoni, H. True and A. P. Engsig-Karup, Sensitivity analysis of the critical speed in railway vehicle dynamics, International Journal of Vehicle Mechanics and Mobility, 52 (1) (2014) 272–286.

    Google Scholar 

  12. J. W. Jang, S. G. Baek, S. W. Lee, Y. S. Choi and J. C. Koo, Optimization of high speed EMU suspension parameters for vibration reduction, Journal of Mechanical Science and Technology, 27 (2) (2013) 305–311.

    Article  Google Scholar 

  13. J. Pombo, J. Ambrósio and M. Silva, A new wheel-rail contact model for railway dynamics, International Journal of Vehicle Mechanics and Mobility, 45 (2) (2007) 165–189.

    Google Scholar 

  14. S. Zhang, S. Sun and X. Jin, Numerical simulation of twopoint contact between wheel and rail, Acta Mechanica Solida Sinica, 22 (4) (2009) 352–359.

    Article  MATH  Google Scholar 

  15. V. K. Garg and R. V. Dukkipati, Dynamics of railway vehicle systems, Academic Press Canada (1984).

    Google Scholar 

  16. D. Horak and D. N. Wormley, Nonlinear stability and tracking of rail passenger trucks, Journal of Dynamic Systems, Measurement and Control, 104 (3) (1982) 256–263.

    Article  MATH  Google Scholar 

  17. P. J. Vermeulen and K. L. Johnson, Contact of nonspherical elastic bodies transmitting tangential forces, Journal of Applied Mechanics, 86 (1964) 338–340.

    Article  Google Scholar 

  18. O. Polach, A fast wheel/rail forces calculation computer code, Vehicle System Dynamics, 33 (1999) 728–739.

    Google Scholar 

  19. J. Halling, Micro-slip between a rolling element and its track arising from geometric conformity and applied surface tractions, Journal of Mechanical Engineering, 6 (1) (1964) 64–74.

    Google Scholar 

  20. SAMCEF 8.3, SAMTECH (2010).

  21. S. H. Han, Dynamics analysis of railway vehicle with creep, M.S. Thesis, Sungkyunkwan University (2014).

    Google Scholar 

  22. N. N. Bogoliubov and Y. A. Mitropolsky, Asymptotic method in the theory of nonlinear oscillations, Hindustan Publishing, India (1961).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, Sungkyunkwan University, 300 Chunchun-dong, Jangan-gu, Suwon, Kyunggi-do, 440-746, Korea

    Yeon-Sun Choi & Bum-Sik Shin

Authors
  1. Yeon-Sun Choi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Bum-Sik Shin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yeon-Sun Choi.

Additional information

Recommended by Associate Editor Eung-Soo Shin

Yeon-Sun Choi received his B.S. degree from Seoul National University in 1976, his M.S. degree from Korea Advanced Institute of Science and Technology in 1978, and his Ph.D. degrees from Texas A&M University, U.S.A, in 1997. He was vice president of the Korean Society for Railway and the Korean Society for Noise and Vibration Engineering, as well as president of the Dynamics and Control Division of the Korean Society of Mechanical Engineers. He is currently a professor at School of Mechanical Engineering, Sungkyunkwan University, Suwon, Korea. His research interests are nonlinear vibration and fault diagnosis of mechanical systems.

Bum Sik Shin received his B.S. degree from Sungkyunkwan University, Suwon, Korea, in 2005 and his M.S. degree from Sungkyunkwan University, Suwon, Korea, in 2007. He is currently a Ph.D. candidate at School of Mechanical Engineering, Sungkyunkwan University, Suwon, Korea. His current research interests include vibration reduction for high speed electric multiple units under development and the structural characteristics of railway vehicle floors.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Choi, YS., Shin, BS. Critical speed of high-speed trains considering wheel-rail contact. J Mech Sci Technol 29, 4593–4600 (2015). https://doi.org/10.1007/s12206-015-1004-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12206-015-1004-2

Keywords

Search

Navigation