Mechanosensing of Cells in Tissue

Cells are subject to mechanical forces produced by actomyosin contraction from within the cell and by external loads. In tissues, cells adhere to the extracellular matrix (ECM) or to neighboring cells through formation of cell–ECM and/or cell–cell junctions (Fig. 1). Fine-tuning transmission of mechanical load from cell to ECM and cell to cell is essential for cell survival, growth, and migration.30,46 Global adaptation of the actomyosin viscoelastic networks and activation of mechanosensitive channels in response to mechanical loads are just two examples of how mechanical forces are transduced into cellular responses.34,40 Recent studies have uncovered a set of mechanosensitive proteins that are responsible for sensing mechanical force and regulating cell–ECM and cell–cell adhesions. These proteins often have a large molecular weight and contain multiple functional modular domains. They are a part of the linkage between the cytoskeleton and cell adhesions, and are subject to tensile force produced by actomyosin contraction.39,41

Figure 1
figure 1

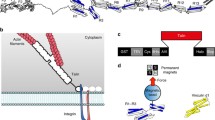
Model of cell adhesions. Cartoon showing two cells adhering to each other and the extracellular matrix. The actin cytoskeleton network provides mechanical linkage between the cells and adhesions. Several known mechanosensitive proteins are highlighted. This cartoon is provided by Alexander Bershadski

Full size image

Cell–ECM adhesions are mediated by the integrin family of cell surface receptors, and recent work has identified a set of integrin-associated cytoplasmic proteins, such as talin, vinculin, and p130Cas, which have buried binding sites for other cellular factors. It has been suggested that mechanical force applied to such proteins may perturb their conformations and expose the buried binding sites, resulting in downstream mechanical signaling processes. For example, experimental evidence suggests that the phosphorylation sites buried in p130Cas can be unmasked upon myosin II-dependent stretching.38 Similarly, many experiments have suggested that mechanosensing processes are also present at cell–cell contacts that are mediated by cadherin-associated adhesion complexes.9,16,23,32

Talin is a large adapter protein that binds integrins, increasing their affinity for the ECM and couples the integrin:ECM complex to cytoskeletal actin1 (Fig. 2a). Talin contains multiple binding sites for the cytoskeletal protein vinculin, which is recruited to adhesion sites by talin to reinforce the link to the actin cytoskeleton. One of the first indications that talin may be mechanically sensitive came from studies looking at talin:vinculin complexes25 and the discovery that the vinculin-binding sites (VBS) in talin, each defined by hydrophobic residues on a single helix, reside within the interior of the folded talin rod domains, suggesting vinculin binding requires unfolding of talin domains to expose these VBS.11,17

Figure 2
figure 2

Talin as a mechanosensor. (a) The classical view of talins function, linking the integrin:ECM complex to the actin cytoskeleton. In this scenario talin experiences force linearly across the whole molecule. (b) The domain structure of full-length talin. Top: structural model and Bottom: schematic of talin. Talin is a large multidomain protein and comprises an N-terminal “head”, that contains an atypical FERM domain (50 kDa), linked via a long unstructured “neck” region (10 kDa) to a large (220 kDa) C-terminal “rod” region. The talin rod is comprised of 13 helical bundles (R1–R13) terminating in a single helix that supports talin dimerization17. The rod contains 11 putative vinculin binding sites (VBS; shown in blue) all of which are buried inside helical bundles. The 5-helix bundles optimized for force transmission are shown in grey. The four 4-helix bundles inserted into this linear arrangement are shown in green. The F-actin and integrin binding sites that serve as force attachment points are marked. (C) 5- and 4-helix bundles have distinctly different unfolding geometries. (d) Two methods of stabilizing 4-helix bundles; R2 is stabilized by an extensive hydrophobic interaction against R1 and R8 is positioned outside the force bearing rod region via insertion into a loop of the R7 domain. (e) Alternate scenarios of force bearing loads on talin resulting from the multiple actin- and integrin-binding sites

Full size image

Based on such studies, it is becoming evident that force-dependent conformation switching of mechanosensitive adapter proteins and the subsequent changes in their binding to other cellular factors may initiate and maintain the cell–ECM or cell–cell adhesions. It provides a general physical molecular mechanism for mechanosensing of cells at the adhesions to sense and adapt to their microenvironments.

Mechanosensitive Functions of Talin

The talin rod contains 13 domains (R1–R13) organized into two functionally distinct regions, a linear C-terminal rod-like region comprised of 5-helix bundles and a compact N-terminal region where three 4-helix bundles (R2–R4) are inserted at the N-terminus of the rod (Fig. 2b).20,21 The linear rod like region is perfectly designed to transmit forces which act on the compact N-terminal region. Through tracking of the two ends of individual talin molecules in vivo, Magardant et al. demonstrated that talin undergoes substantial structural fluctuations when subjected to cellular actomyosin forces.31 The classical view of talin, bound to integrin at the N-terminus and actin at the C-terminus (Fig. 2a), means that the forces exerted on talin are uniform across the whole molecule.

The 5-helix bundle topology found in talin domains R1, R5–R7, and R9–R12 is unique to talin and, with the N- and C-termini positioned at opposite ends of the domain, is optimal for forming a linear chain and perfectly suited to force transmission.21 The cluster of 4-helix bundles, R2–R4, has a markedly different topology, with the N- and C-termini at the same end of the bundle. This difference in topology of the bundles means that they have fundamentally different force responses; 4-helix bundles have an unzipping force response whereby 5-helix bundles have a shearing force response (Fig. 2c). It has been shown that the unzipping force geometry can withstand less rupture force compared to that in the shearing force geometry.6,37 Indeed, what we see from our single molecule stretching experiments is that the 4-helix bundles unfold at ~5–10 pN forces, while the 5-helix domains unfold at significantly larger forces. Under force, these results suggest that 4-helix domains in the talin rod unfold first due to their unzipping force geometry, and their mechanically exposed VBS are likely to be among the first to bind vinculin.

4-Helix bundles also act as binding sites for many proteins and as such when talin is under tension these binding surfaces will be disrupted first. This is the case for the interaction of talin with the RAP1 GTPase effector, RIAM. Talin contains several binding sites for RIAM, which is involved in recruiting talin to the plasma membrane.29 RIAM binds synergistically and with high affinity to the folded R2–R3 4-helix bundles in the N-terminal region of the talin rod domain. The implication of this is that talin switches binding partners in response to force induced conformational changes. At low forces, RIAM binding to talin R2R3 would predominate, supporting talin recruitment to the membrane, integrin activation, and the assembly of nascent adhesions. But at around 5 pN, R3 unfolds disrupting the RIAM binding sites resulting in a transition to vinculin:talin complexes which drives the maturation of nascent adhesions into focal adhesions.

The fact that the 4-helix bundles will be the first domains to unfold means that these bundles and binding sites will be disrupted at moderately low forces, <10 pN. Interestingly, two of these 4-helix bundles are able to withstand higher forces due to novel structural features. The R2 domain is stabilized via a hydrophobic packing interaction with R1, a 5-helix bundle. This not only stabilises the bundle but augments the unfolding geometry such that it is more shear like (Fig. 2d). Secondly, there is an additional 4-helix bundle, R8, which gets around this mechano-susceptibility by being inserted into a loop of a 5-helix bundle, creating a novel 9-helix module and a branch in the talin rod (Fig. 2d). By being outside of the force bearing region it is likely that it remains folded whilst talin is under force and maintains its ligand binding surface.

Finally, we note that the situation is complicated by the presence of both an additional actin-binding site and a second integrin-binding site in the talin rod, raising the possibility of differential forces being exerted on the molecule. Furthermore, full-length talin is dimeric18 increasing the number of potential attachment sites (Fig. 2e). Evidence that these additional attachment points might affect adhesion dynamics came from a recent study by Zhang et al. who identified a C-terminal fragment of talin potentially liberated by exposure of a hidden calpain-sensitive cleavage site by force-induced conformation changes of talin.47 This C-terminal fragment was shown to play an important and unexpected role in maintaining cell–cell junctions.47 Two non-force modulated calpain cleavage sites have already been identified in talin,13,47 and calpain-mediated proteolysis of talin regulates adhesion dynamics. However, the precise forces and conditions where this mechanosensitive site is exposed remain to be characterized.

Studying Single Mechanosensing Proteins Using Magnetic Tweezers

When a tensile force is applied at two anchoring points of a protein, the protein may deform or undergo structural transition. Such force dependent conformational changes may affect its interaction with its binding partners, resulting in force sensing. Studying such mechanosensing mechanisms at a single-molecule level requires technologies that can apply force to single, short protein tethers, and examine its deformation and structural changes as well as its force-dependent binding to other factors. Among several single-molecule manipulation technologies, magnetic tweezers have many unique advantages in terms of instrumentation simplicity and stability, experimental throughput, easy temperature control and solution exchanging.7

A typical magnetic tweezers setup design is illustrated in Fig. 3a. The molecule to be studied is tethered between a coverslip and a paramagnetic bead, with both surfaces chemically functionalized for specific attachment of the protein. Force is generated by a pair of permanent magnets to the bead, and the extension change of the tether is recorded at a nanometer resolution based on the diffraction pattern of the bead.19 By closing the gap between the two permanent magnets using back scattered illumination, the force range can be significantly increased.3 Such magnetic tweezers have been shown to be capable of direct stretching of both short DNA and protein tethers at large applied forces4,14,15,45 and have been used by us to investigate the mechanosensing mechanisms of talin and α-catenin.43,44

Figure 3
figure 3

The force induced unfolding of talin R1–R3 domains. (a) Schematic of magnetic tweezers. The individual protein of interest is specifically tethered between a cover slip and a paramagnetic bead. Forces are applied to the bead by a pair of permanent magnets. (b) Time lapse of the near-equilibrium unfolding/refolding fluctuation of talin R3 domain at ~5 pN forces. (c) Force-extension curves of five consecutive pulls of a talin R1–R3 molecule in the absence of vinculin head. The triple domain unfolds in three discrete steps consistent with the three domains unfolding independently. Data in (b) and (c) are adapted from our previous publication with permission.43

Full size image

Force Responses of Talin Domains

Steered molecular dynamics simulations on the N-terminus of talin (residues 482–889, which is R1–R2 plus 3 helices in R3) have suggested that force may expose the cryptic VBS for vinculin binding.24,28 AFM studies have shown that this region unfolds at forces below 20 pN,8 but the force responses of single talin rod domains were not determined. Recently the force response of the first three rod domains of talin, R1–R3, was investigated using magnetic tweezers,43 which demonstrated that the domains unfold individually at different forces. The R3 4-helix bundle was shown to be the weakest domain, unfolding at ~5 pN force which is insensitive to loading rate of force (Fig. 3b). This instability is due to the unzipping force geometry and a unique cluster of threonine residues buried within the hydrophobic core of the bundle that destabilize it.21,43 Rapid equilibrium fluctuations between the folded and unfolded states were observed around the unfolding force, 5 pN, with a transition rate of several seconds (Fig. 3b). In spite of the weak unfolding force for the R3 domain, a large energy cost of more than 10 k B T is needed for the unfolding due to the large unfolding step size of ~16 nm. Therefore, thermal fluctuation, which involves k B T energy scale, would not cause spontaneous unfolding.

The other two domains unfold at >15 pN at a loading rate of 5 pN/s (Fig. 3c), with weak dependence on loading rate (unpublished). Equilibrium folding and unfolding transitions of these domains were not observed at constant forces over long experimental time scales, suggesting a large energy barrier separating the folded and unfolded states of these two domains. Strikingly though, all the talin rod domains unfolded by force were able to rapidly adopt their folded conformation once the force was released. These results support a model in which the talin R3 domain unfolds first upon stretching at nascent focal complexes, and at a force level that can be generated by a single myosin.12 Unfolding of the other domains may follow if the tension builds up as the adhesion matures.

Force Dependent Binding of Talin R1–R3 to Vinculin Head

Previous single-molecule photobleaching experiments revealed that application of ~12 pN force on the talin N-terminus significantly increased the amount of the vinculin head domain, Vd1, bound to talin.8 Consistently, a more recent study showed that forces applied to full-length talin by actomyosin contraction through actin cables resulted in increased level of vinculin binding to talin.5 In our recent study, we examined how the force-dependent structures of talin R1–R3 domains are coupled to Vd1 binding at a single molecule level. The main findings are summarized below.

We showed that when force is applied to R1–R3, the individual domains unfold and expose their vinculin binding sites (VBS). Figure 4a shows one such exposed VBS bound with a Vd1 molecule. Vd1 binds to the exposed VBS with nanomolar affinity and inhibits the refolding of the talin rod. By inhibiting the refolding of talin (Fig. 4b), vinculin acts like a switch that leads to stable subsequent cellular responses.

Figure 4
figure 4

Force dependent interaction between talin R1–R3 and vinculin head (a) Crystal structure of vinculin Vd1 domain (1-258) binding to a VBS peptide. The VBS peptide adopts α-helix conformation in the bound form. This illustration is made with VMD program22 based on PDB structure 1SYQ.25 In our experiments, the exposed VBS bound with Vd1 is under force indicated by arrows. (b) Mechanosensitivity of talin R1–R3. After incubation with 10 nM Vd1, the characteristic unfolding steps were observed in the first force stretching (red). Unfolding events were absent in subsequent stretches after talin R1–R3 was allowed to refold at low forces (black), indicating complete inhibition of talin rod refolding by vinculin head bound to mechanically exposed VBS in the first stretch. (c) Time-lapse data of talin R1–R3 in 0 nM (red) and 10 nM (black) of vinculin head during force jumping between 6 pN for 1 min, during which no domain refolding was observed (pink/grey), and 40 pN for 5 s (red/black). For clarity, the curves are shifted along the extension-axis to avoid overlapping. Each unfolding step observed at 40 pN indicates dissociation of a Vd1 from talin. Inset shows histogram of the unfolding step sizes at 40 pN. Data in (b) and (c) are adapted from our previous publication with permission.43

Full size image

Interestingly, when the force applied to talin exceeds 30 pN, bound Vd1 molecules start to dissociate from talin, resulting in a ~3 nm increase in the extension (Fig. 4c). This is driven by the force-induced destabilization of the VBS α-helix, causing it to undergo a helix-to-coil transition displacing the bound Vd1. This force range is physiologically relevant as recent experiments have suggested that the forces acting on a single integrin molecule in mature focal adhesions are >40 pN.42 Furthermore, this extension increase due to displacement of bound binding partner at higher forces allows direct quantitation of the stoichiometry of the interaction; in the case of R1–R3 binding to vinculin, we observed up to five 3 nm extensions indicating displacement of up to five vinculin molecules.

R2–R3 also forms the high affinity RIAM binding site, and with a 5 pN force being sufficient to unfold the R3 domain, it is likely that this would destroy the high affinity RIAM binding site whilst simultaneously exposing the high affinity vinculin binding sites. As the switch between talin:RIAM and talin:vinculin complexes is likely to be key to adhesion regulation it will be important to investigate further this force dependent binary switch.

Understanding Mechanosensing Mechanisms

As shown in our studies of force dependent talin deformation and talin–vinculin interactions, force dependent conformational changes of talin drastically affect its interaction with the vinculin head.43 By exposing the buried VBS in talin R1–R3 forces in the 5–30 pN significantly enhance the binding of vinculin head to the talin rod; decreasing the binding dissociation constant from previously reported μM range from test tube experiments (in the absence of force)2 to nM range from our single-molecule assay.43 This section discusses the physics underlying these observations.

Force Dependent Stability of Protein Structures

The distance between the two anchoring points along the force direction, namely the extension (x), changes with force, leading to a force extension curve x i(F, ξ) that depends on the particular structural state indexed by the subscript “i” of the protein. ξ is a parameter vector describing solution conditions such as temperature, salt concentration, and pH. In a simplified model, a talin rod domain has three structural states: the natively folded helix bundle state “0”, an unbundled chain of a series of α-helices “α”, and a disordered peptide chain state “c”, each associated with a free energy G i(F, ξ):

$$G_{0} \left( {F,{\varvec{\xi}} } \right) \, = \Phi_{0} (F,{\varvec{\xi}});\;G_{\alpha } \left( {F,{\varvec{\xi}} } \right) \, = \varepsilon + \Phi_{\alpha } (F,{\varvec{\xi}});\;G_{\text{c}} \left( {F,{\varvec{\xi}} } \right) \, = \mu + \varepsilon + \Phi_{\text{c}} (F,{\varvec{\xi}}).$$
(1)

Here the force independent term ε denotes energy cost to unbundle the natively folded state, and μ denotes energy cost to further unfold the unbundled chain of α-helices into the disordered peptide chain state. One would expect a large unbundling energy cost ε for talin rod domains and a much weaker helix-to-coil transition energy μ (ε ≫ μ > k B T). Φi (F, ξ) = −∫ F0 x i (f, ξ) df denotes the force-dependent conformational free energy of a particular state “i”, where x i(f, ξ) is the extension of the molecule at the state “i” at force “f”. Here, the ground state with a zero free energy has been chosen as the natively folded state under zero force. At equilibrium, the probability of a state follows the Boltzmann distribution:

$$P_{\text{i}} = {\text{Z}}^{ - 1} { \exp }( - G_{\text{i}} (F,{\varvec{\xi}} )/k_{\text{B}} T),$$
(2)

where Z = exp(−G 0(F, ξ)/k B T) + exp(−Gα(F, ξ)/k B T) + exp(−G c(F, ξ)/k B T) is the partition function. A force induced transition from a state “i” to another state “j” is associated with a Gibbs free energy change of ∆G ij(F, ξ) = G j(F, ξ) − G i(F, ξ), which is statistically favored if ∆G ij(F, ξ) < 0.

The above theoretical framework is based on equilibrium statistical mechanics, which provides an overall understanding of the force-dependent states of the talin rod domains. In vivo, the talin molecule is stretched by actomyosin contraction where force is varying and under certain loading rate. The physiologically relevant loading rate of force on single proteins in focal adhesion sites was estimated to be in the range of 0.001–4 pN/s,33,36 which is close to that used in Fig. 2. The sensitivity of unfolding force to loading rate in general depends on the transition distance.10,27 Our data have shown that the talin R3 domain has a large transition distance resulting in insensitivity to loading rate.43 Regarding the R1 and R2 domains, we found that they have a weak dependence on loading rate—changing loading rate from 0.4 to 4 pN/s only increased unfolding force by ~10% (unpublished data). We expect that the other domains in the full-length talin rod have a similar weak loading rate dependence. The insensitivity of unfolding force to loading rate may have an advantage in making talin a robust force sensor.

Force-Dependent Binding of Vinculin Head to a Talin Rod Domain

Vd1 binds to the unbundled state “α” of talin rod, resulting an additional bound state “α + Vd1”. This new state is associated with a free energy of:

$$G_{{\alpha + {\text{Vd1}}}} \left( {F,{\varvec{\xi}} } \right) \, = \, - k_{\text{B}} T\ln\left( {c_{\text{Vd1}} /k_{{{\text{D}}0}} } \right) \, + \varepsilon + \Phi_{{\alpha + {\text{Vd1}}}} (F,{\varvec{\xi}}),$$
(3)

where c Vd1 is the Vd1 concentration, and k D0 is the dissociation constant between Vd1 and the constitutively active unbundled state “α” of talin rod. An effective force-dependent dissociation constant can be defined by: P α+Vd1/P unbound = c Vd1/k D(f), where P unbound refers to the probability of all unbound states: P unbound = P 0 + P α  + P c. Therefore,

$$k_{\text{D}} \left( F \right) = k_{{{\text{D}}0}} { \exp }(\Phi_{{\alpha + {\text{Vd1}}}} /k_{\text{B}} T)\{ { \exp }((\varepsilon - \Phi_{0} )/k_{\text{B}} T) + { \exp }( - \Phi_{\alpha } /k_{\text{B}} T) + { \exp }( - (\Phi_{\text{c}} + \mu )/k_{\text{B}} T)\}$$
(4a)
$$\sim k_{{{\text{D}}0}} \{ 1+ { \exp }((\varepsilon + \Phi_{\alpha } - \Phi_{0} )/k_{\text{B}} T) \, + { \exp }((\Phi_{\alpha } - \Phi_{\text{c}} ) - \mu )/k_{\text{B}} T)\} .$$
(4b)

In the second step we have approximated Φ α+Vd1(F, ξ) ~ Φ α (F, ξ) based on an assumption that an α-helix is a rigid body thus its force-extension curve is not sensitive to binding by Vd1.

Biphasic Force Dependence of Vinculin Binding

At zero force, Φi (F) = 0 for all the states, so Eq. (4) is simplified as:

$$k_{\text{D}} \left( 0 \right) = k_{{{\text{D}}0}} \{ 1+ { \exp }(\varepsilon /k_{\text{B}} T) \, + { \exp }( - \mu /k_{\text{B}} T)\}$$
(5)

According to Eq. (5), k D(0) > k D0, indicating auto-inhibition of Vd1 binding to the active unbundled state of talin due to the presence of the two inactive states “0” and “c”, which exponentially increases as ε increases. k D(0) ~ k D0 exp(ε/k B T) since ε ≫ μ, meaning that the auto-inhibition effect is predominately caused by a large unbundling free energy cost ε.

In moderate force range when the magnitude of Φ α –Φ0 is larger than or comparable to that of Φ α –Φc, one can derive from Eq. (4b):

$$k_{\text{D}} \left( F \right) \, \sim k_{{{\text{D}}0}} \{ 1+ { \exp }((\varepsilon + \Phi_{\alpha } - \Phi_{0} )/k_{\text{B}} T) \, \}$$
(6)

If ΔΦ0α (F, ξ) = Φ α (F, ξ) − Φ0(F, ξ) < 0 which facilitates unbundling transition, k D(F) decreases and approaches toward k D0, indicating release of auto-inhibition by mechanically exposing the buried VBS binding sites in talin rod.

At large force where ΔΦ αc(F, ξ) = Φc(F, ξ) − Φ α (F, ξ) becomes negative with a magnitude ≫k B T, the contribution of the term exp((Φ α (F, ξ) − Φc (F, ξ))/k B T) in Eq. (4b) can no longer be ignored. Its net effect is to increase k D(F) by favoring a helix-to-coil transition to the disordered peptide chain state that does not bind Vd1.

In summary, the above theoretical analysis based on equilibrium statistical physics provides a qualitative understanding of the observed biphasic force dependent Vd1 binding to talin rod domains. The apparent force dependent dissociation constant decreases in a moderate force range but it increases at further increased forces, which is due to the presence of several force-dependent structural states of the talin rods with distinct force responses. A quantitative comparison between the theoretical model and the experiments requires precise knowledge on the force-extension curves of each of the structural states as well as the unbundling and the helix-to-coil transition free energy costs (ε and μ), which warrants future study and is beyond the scope of this mini-review.

Biological Implications and Outlook

With the recent advancements in single-molecule manipulation technology it is now feasible to study complex mechanobiochemistry in vitro and the strategies described here to study biochemistry in the presence of physiologically relevant forces can be expanded to investigate every domain in talin, both individually, in multi-domain fragments and ultimately in the context of the entire molecule. This will enable a complete understanding of talin’s complex role as a mechanosensor. Furthermore, there are many other proteins that bind to the cytoskeleton upon stretch,38 and it is likely that many will rely upon exposure of buried binding sites. The approaches described here can be applied to getting detailed understanding of other mechanosensitive proteins.

Recent studies have provided direct evidence that mechanical force of 5–30 pN can expose buried vinculin-binding α-helices in talin, activating binding of the head domain of vinculin. This fits with a model where only when the talin starts to engage the β-integrin tail and acidic membrane phospholipids via its N-terminal head domain and captures the retrograde flow of actin filaments at the leading edge via its C-terminal actin binding site, will the talin rod experience the tension required to expose its vinculin binding sites. The force-dependent dissociation constant in nM range is ~103 smaller than Vd1 binding to folded talin rod domains, translating into an ~7 k B T inhibitory energy barrier for Vd1 binding to folded talin rod domains that is removed by force. Such a high affinity interaction between vinculin head and mechanically exposed vinculin binding α-helices in talin may be able to compete off the auto-inhibitory head-to-tail association in full-length vinculin.26 As full-length vinculin contains binding sites for numerous cellular binding partners regulating focal adhesions, cell–cell junctions, and cell motility,35 force-activation of vinculin may result in subsequent vinculin dependent cellular signaling.

It is possible that the 5 pN low force threshold that we have identified in talin, which corresponds to the force exerted by a single actomyosin contraction, may be a common feature of other mechanosensitive proteins that couple to actin. Indeed, we have recently identified a similar force threshold in α-catenin (a force sensing protein at cell–cell junctions), where a force greater than 5 pN also exposes a vinculin-binding site increasing the binding affinity for vinculin a thousand fold.44 Interestingly, at the force threshold of mechanosensitive domains, rapid unfolding/refolding fluctuations are observed suggesting that the unfolding event is very dynamic, and can rapidly refold in the absence of other factors.

Many proteins have been shown to bind to cytoskeletons upon stretch and likely rely upon similar exposure of buried binding sites by force. Thus, force-induced protein–protein interactions might be a general mechanism for ensuring that binding interactions only occur in the force range required to support physiological functions. Future studies should be directed to quantify force-dependent protein–protein interactions that are involved in various disease related cellular processes, and to the discovery of mechano-active small molecules and peptides that bind to mechanosensing proteins. As well as being useful as research tools to manipulate force-dependent interactions of mechanosensing proteins, such mechano-active small molecules and peptides have the potential to evolve into a new generation of drugs targeting disease-related mechanosensing pathways.

In summary, the emerging picture of how talin functions as a mechanosensor is much more complex than initial studies suggested, undergoing a progressive mechanoresponse to the varying forces exerted on the molecule throughout adhesion and migration. These features include (i) force dependent conformational changes, ligand binding sites that are (ii) disrupted (RIAM) and (iii) exposed (vinculin) by force, and (iv) force-induced conformational changes in talin exposing hidden protease cleavage sites. It is likely that additional ligand binding peptide motifs, cryptic cleavage sites and phosphorylation sites may be revealed/disturbed by force and with the presence of several actin and integrin binding sites affecting how and when force acts upon talin further investigation will be required to fully understand this master mechanosensor.