1 Introduction

Cancer is one of the non-communicable diseases that remains a significant public health challenge and a leading cause of death worldwide. It is characterized by the uncontrolled growth and spread of abnormal cells in the body. According to the National Cancer Institute (NCI), there are more than 100 types of cancer [1]. As reported by the World Health Organization (WHO) [2], the most prevalent types of cancer vary between genders. In men, lung, prostate, colorectal, stomach, and liver cancer are frequently reported. Conversely, among women, breast, colorectal, lung, cervical, and thyroid cancer are the most commonly diagnosed.

Researchers have worked intensively to find an effective cancer treatment, and this endeavor has continued to the present day. These efforts have revealed a plethora of treatment modalities, among which surgery stands prominent, particularly recommended for earlystage solid tumors [3]. Additionally, modalities such as chemotherapy, radiotherapy, immunotherapy, and gene therapy have been investigated [4]. Consequently, approaches such as combining surgery with chemotherapy or radiation therapy or combining immunotherapy with chemotherapy have been investigated to enhance the overall effectiveness of the treatments [5,6,7]. However, most cancer treatments have shortcomings and entail side effects. For instance, In some cases, surgery alone is not enough to remove the tumor from the patient’s body; chemotherapy or radiotherapy might need to be followed [8]. Furthermore, while chemotherapy is effective at killing tumor cells, it also causes toxicity and can harm normal and immune cells [9].

Another significant challenge in cancer treatment is the development of drug resistance by cancer cells to traditional therapies, such as chemotherapy and radiotherapy [10,11,12,13]. This resistance can significantly limit the treatment efficacy and may even increase the risk of treatment failure [10, 11].

In response to these challenges, particularly the issues of toxicity and drug resistance, the field has increasingly turned to virotherapy as a promising alternative.

Oncolytic virotherapy or oncolytic viruses (OVs) drug is categorized as an immunotherapy and is one of the most commonly used cancer treatments. Virotherapy treats various cancer types, including melanoma, leukemia, breast cancer, prostate cancer, brain tumors, and lung cancer  [14]. Moreover, oncolytic virotherapy is considered one of the best cancer treatment options due to its low impact on normal and immune system cells, leading to lower toxicity [15, 16]. The dynamic of OVs is represented by selectively replicating in tumor cells. This replication results in either a direct effect, such as the lysis of tumor cells, or an indirect effect, where oncolytic virotherapy can affect tumor cells, aiding the immune system in recognizing and eradicating these cells [14, 17].

Although OVs have the ability to induce tumor oncolysis and attract the response of anti-tumor immune cells such as T cells, studies showed that OVs alone may not be enough for complete tumor elimination [18]. These limitations arise because oncolysis alone is insufficient to eradicate tumors or to stimulate a robust anti-tumor response. However, in response to this inadequacy in the ability of OVs to stimulate the anti-tumor immune response, the concept of incorporating immunostimulatory molecules, such as cytokines, has emerged. This idea aims to enhance the stimulation of a robust anti-tumor response and tumor clearance [18].

Cytokines play a significant role in tumor development and progression, serving as cell-cell communication mechanisms between immune and tumor cells [19, 20]. Additionally, they are used to enhance the recruitment of immune cells to the tumor microenvironment through a process known as chemotaxis [21]. These soluble proteins are naturally present in the body and released by various types of immune cells. Primarily, the production of these proteins is attributed to lymphocytes, secreted by T cells, B cells, and natural killer cells, along with monocytes, released by macrophages and dendritic cells [22]. The categorization of cytokines is based on their way of secretion into four types: lymphokines, monokines, chemokines, and interleukins, which are produced by lymphocytes, monocytes, chemotactic activities, and leukocytes, respectively [23].

In this study, our main focus will be on one of these cytokines, namely interleukin-2 (IL-2).

IL-2 plays an important role in cell-cell communication between tumor and immune cells. Mostly, this cytokine is released by immune cells, such as CD8\(^+\) cytotoxic T lymphocytes (CTLs) and natural killer (NK) cells. This cytokine is used to stimulate these cells by increasing their anti-tumor and cytotoxic activities [24,25,26].

In the tumor-virotherapy microenvironment, IL-2 plays an important role in enhancing virotherapy. In addition, the combination of IL-2 with virotherapy plays a crucial role in compacting resistance to traditional treatments [27]. Kottke et al. [28, 29], demonstrated that combining IL-2 with virotherapy enhances treatment. This enhancement is evident through their contribution to generating highly activated natural killer cells that exhibit potent anti-tumor activity. Furthermore, they contribute to the spread of viruses throughout the tumor. IL-2 also plays a crucial role within tumor cells, as studies have indicated that the presence of IL-2 has the capability to increase apoptosis levels within infected cells [30]. Consequently, this phenomenon enhances the effectiveness of the tumor-selective parental virus, transforming it into a more potent agent for combating cancer [30]. Conversely, a high concentration of IL-2 can act as an environmental cue to induce CD8\(^+\) T cells. However, the exhaustion of CD8\(^+\) T cells can weaken the effectiveness of the anti-tumor immune response [31]. Simultaneously, high doses of IL-2 can lead to several side effects, including fever, chills, hypotension, tachycardia, oliguria, nausea, vomiting, diarrhea, capillary leak syndrome, renal failure, cardiac toxicities, and thrombocytopenia [32, 33]. To mitigate the side effects associated with administering IL-2 systemically throughout the entire body, Liu et al. [34] employed a technique in which IL-2 is attached to the membrane of tumor-targeted oncolytic vaccinia virus. This approach aided in expanding the population of T-cells and limited the side effects associated with the traditional systemic administration of IL-2.

Boosting the infiltration of immune cells within the tumor-virotherapy environment can enhance their capacity to detect and eliminate cancerous cells. However, this heightened immune presence may accidentally boost antiviral activity within these cells, leading to increased viral clearance and potentially reducing the effectiveness of virotherapy treatments [35]. To mitigate this issue, researchers have suggested several strategies. These strategies include the use of protective coatings with chemical polymers, liposomes, or cell-derived nanovesicles to protect OVs physically against immune factors [36].

In recent decades, many mathematical models have been developed to describe the dynamic interaction between OVs, tumor cells, and immune system response [16, 37,38,39,40,41], and more recently [42].

Vithanage et al. [40], developed a mathematical model that describes the dynamic interactions between uninfected tumor cells, infected tumor cells, oncolytic virotherapy, and immune cells. The model investigates the dual role of immune cells within the tumor-virotherapy microenvironment. In this framework, immune cells are assumed to target both tumors and free viruses, which can reduce viral infection. The findings indicate that complete tumor elimination is possible when the killing rate of the tumor by immune cells is larger than the growth rate of the tumor. However, in weak immune responses, tumors grow large, and virotherapy fails. Besides that, their study demonstrates that the effectiveness of virotherapy is enhanced when the immune cells show a lower clearance rate for the virus, and in contrast, reduced efficacy is observed when the clearance rate is higher.

Vithanage et al. [41], extended the model introduced in [40] by incorporating two new components: continuous doses of virotherapy and adopted T cell transfer. They employed optimal control techniques to minimize the number of susceptible tumor cells as well as the associated costs of therapy during the treatment period. Numerical simulations with different scenarios for initial tumor sizes and parameter values were conducted. The results revealed that the therapy does not work synergistically under a high viral clearance rate by immune cells, while under a low viral clearance, it can improve therapy success through virotherapy alone or combined with adopted T-cell transfer.

Salma et al. [37], presented a mathematical model that describes the interaction dynamic of virotherapy, tumor cells, and immune response was presented. The results showed partial success in virotherapy under the condition that the burst size should be greater than the rate at which immune cells kill OVs and when there is a high infection rate. Furthermore, the results indicated that the number of viruses would be high in the tumor microenvironment when the infection rate is high, and the stimulation rate of the immune cell response by uninfected tumor cells is low. Notably, in both scenarios, these conditions led to a reduction in tumor size.

Malinzi et al. [38], presented a mathematical model that describes the interaction dynamics of the tumor cells, immune response, and a combination of chemotherapy and oncolytic virotherapy. The results of their study showed the ability of chemotherapy alone to eliminate tumors when its efficacy is greater than the growth rate of tumor cells. Furthermore, the results indicated that virotherapy as an individual treatment may not be able to eliminate tumors, instead enhance the efficacy of chemotherapy if high-potency viruses are used.

Senekal et al. [39] presented a mathematical model investigating the role of NK cells in the tumor-virotherapy microenvironment. The results of this study revealed that for virotherapy to be successful, the recruitment of NK cells to the tumor-virotherapy microenvironment should occur neither too early nor too late during OV infection.

Although certain studies have indicated that the high presence of immune cells in the tumor-virotherapy microenvironment can induce an anti-viral response, potentially negatively affecting the efficacy of virotherapy (see [35, 43]), others have demonstrated that a weak immune response in the tumor-virotherapy microenvironment may result in a large growth of tumor cells and a potential failure of virotherapy [40].

This study aims to explore the dynamic interactions between tumor cells and virotherapy, with a focus on harnessing the cytokine IL-2 to enhance the recruitment and activation of immune cells within the tumor microenvironment. By applying optimal control techniques, we aim to minimize the number of infected and uninfected tumor cells as well as determine the most effective protocol for the administered treatment.

This paper is structured as follows. In Sect. (2), we briefly show the development of our system in the form of a system of ordinary differential equations. Section (3) is dedicated to model analysis, where we examine the positivity and boundedness of the solutions. Furthermore, we nondimensionalize the model and analyze its stability, examining scenarios with and without external doses. In Sect. (4), we conduct a sensitivity analysis of the model’s parameters to identify those with the most significant impact on the growth of tumor cells. In Sect. (5), we establish our optimal control problem, examine its existence, and derive the necessary conditions for the optimal control strategies. Section (6) presents the numerical simulations. Finally, Sect. (7) summarizes and discusses our conclusions.

2 Mathematical model

2.1 Model formulation

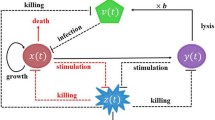
In this section, we introduce a mathematical model that describes the dynamic interactions between various populations, including uninfected tumor cells, infected tumor cells, OVs, immune cells, and the cytokine IL-2.

The populations at time t are denoted by:

  • U(t), the concentration of uninfected tumor cells,

  • I(t), the concentration of infected tumor cells,

  • V(t), the population of oncolytic viruses,

  • M(t), the concentration of immune cells,

  • N(t), the concentration of interleukin-2 (IL-2).

In this study, we consider the immune cells to be the tumor-infiltrating cytotoxic lymphocytes (TICLs). These cells are the most important (specific) antitumor effector cells, and they include cytotoxic T-lymphocytes (CD8\(^+\) T cells), CD4\(^+\) cells, NK cells, B lymphocytes (B cells), and other immune cells.

Our system of equations, which describes the interactions between these compartments, is presented as follows:

$$\begin{aligned} \frac{dU}{dt}= & {} \alpha U\left( 1 - \frac{U + I}{R}\right) - \beta UV - k_1MU - d_UU, \end{aligned}$$
(1)
$$\begin{aligned} \frac{dI}{dt}= & {} \beta UV - k_2IM - d_II, \end{aligned}$$
(2)
$$\begin{aligned} \frac{dV}{dt}= & {} bd_II - \beta UV - d_V V - k_4 VM + u_1(t), \end{aligned}$$
(3)
$$\begin{aligned} \frac{dM}{dt}= & {} s + p_1(U+I)M + \frac{p_2MN}{q_2 + N} - k_3MU - d_MM, \end{aligned}$$
(4)
$$\begin{aligned} \frac{dN}{dt}= & {} \frac{p_3UM}{q_3 + U} - d_NN + u_2(t), \end{aligned}$$
(5)

with non-negative initial conditions \(U(0)= U_0\), \(I(0)= I_0\), \(V(0)= V_0\),\(M(0) = M_0\), and \(N(0) = N_0\).

In Fig. (1), we show the schematic diagram of the interaction between the population densities in the model (1)–(5). The descriptions of model parameters are given in Table (1).

In Eq. (1), the term \(\alpha U\left( 1 - \frac{U + I}{R}\right) \), represents the logistic growth of tumor cells, as assumed in [38, 39], where \(\alpha \) denotes the growth rate, and R is the carrying capacity. The term \(\beta UV\) represents viral infection of tumor cells, with \(\beta \) denotes the infection rate. \(k_1MU\) represents the killing of uninfected tumor cells by immune cells. The parameter \(k_1\) represents the killing rate. The natural death of uninfected tumor cells is given by the term \(d_UU\), where \(d_U\) is the death rate.

In Eq. (2), the term \(k_2IM\) defines the killing of infected tumor cells by immune cells, whereas \(k_2\) represents the killing rate. The natural death rate of infected tumor cells is given by the term \(d_II\), where \(d_I\) is the death rate.

Equation (3) describes the dynamic of OVs. The term \(bd_II\) represents the newly released viruses from the lysed infected tumor cells. The parameter b, represents the viral burst size. The OVs decay over time, and this decay is denoted by the term \(d_VV\), where \(d_V\) is the decay rate. The term \(k_4 VM\) represents the clearance of the free OVs by immune cells, where \(k_4\) is the virus clearance rate. Furthermore, this assumption is valid only if the killing rate of the OVs by immune cells is less than the replication rate of the OVs [39, 44, 45]; if the killing rate of the OVs by the immune cells is greater than the replication rate, that can cause the failure of the virotherapy. The direct injection of free viruses is represented by the term \(u_1(t) (u_1(t) = u_1)\). In Eq. (4), the term s represents a constant source for immune cells. The term \(p_1(U+I)M\) represents the stimulation of the immune cells’ response by uninfected and infected tumor cells, where \(p_1\) is the stimulation rate. The interaction between immune cells and uninfected tumor cells can lead to the release of various signaling molecules, including IL-2; IL-2, in turn, activates and recruits immune cells to the tumor microenvironment. The activation of immune cells through IL-2 can be described by the term \(\frac{p_2MN}{q_2 + N}\), where \(p_2\) is the maximum immune cells recruitment rate by IL-2 and \(q_2\) is the Michaelis-Menten constant, representing the concentration of IL-2 required to achieve half-maximal activation of immune cells [46]. The term \(k_3MU\) refers to eliminating immune cells by the uninfected tumor cells, where \(k_3\) is the killing rate. The natural death of immune cells is represented by the term \(d_MM\), where \(d_M\) is the death rate.

In Eq. (5), the Michaelis–Menten term \(\frac{p_3UM}{q_3 + U}\) represents the secretion of IL-2 through the interaction between immune and uninfected tumor cells as described in [46]. Here, \(p_3\) represents the maximum recruitment rate of IL-2 from tumor-immune cell interactions, and \(q_3\) is the Michaelis-Menten constant, representing the concentration of tumor antigens required to achieve half-maximal activation of immune cells. The Michaelis-Menten kinetics \(\frac{p_3UM}{q_3 + U}\) is for the self-limiting production of IL-2 [47]. This self-limiting behavior ensures that the concentration of IL-2 does not become excessively high, which could lead to overstimulation of immune responses or potential harmful effects. Instead, it helps maintain a balanced immune response by regulating the production of IL-2 in response to the needs of the immune system. This means that the rate of IL-2 production increases with the number of uninfected tumor cells U but approaches a maximum limit as U becomes very large. This prevents the unlimited increase in IL-2 production, which is crucial to avoid potentially damaging hyperactive immune responses. The term \(d_NN\) represents the decay rate of IL-2, where \(d_N\) is the rate of decay. The term \(u_2(t) (u_2(t) = u_2)\) represents the direct injection of IL-2.

Table 1 Description of the parameters in the model
Full size table
Fig. 1
figure 1

The diagram shows the dynamic interactions between different populations within a tumor microenvironment, which include uninfected tumor cells (U), infected tumor cells (I), OVs (V), immune cells (M), and IL-2 (N)

Full size image

2.2 Parameter estimation

To complete our model formulation, we need to determine the parameter values for our model equations (1)- (5). Currently, there are no longitudinal data available on the combined use of virotherapy and IL-2. Therefore, for our model simulations, we selected parameter values from the published literature that closely align with the experimental data on virotherapy and IL-2. The selected parameter values are given in Table 1.

3 Model analysis

3.1 Positivity and boundedness of solutions

In this section, we show the well-posedness of the system  (1)–(5) and prove that the solutions are biologically meaningful. In order to show that, it is required to prove that the solutions of the system are both positive and bounded for all time.

Theorem 1

(Positivity) For given \(U(0)\ge 0 \), \(I(0)\ge 0 \), \(V(0)\ge 0 \), \(M(0)\ge 0 \) and \(N(0)\ge 0 \) for all \(t \ge 0 \), then the solutions U(t), I(t), V(t), M(t), and N(t) of the system (1) - (5) will always remain non-negative.

Proof

From system (1)–(5), we have

$$\begin{aligned} \left. \frac{dU}{dt}\right| _{U=0}&= 0, \\ \left. \frac{dI}{dt}\right| _{I=0}&= \beta UV, \\ \left. \frac{dV}{dt}\right| _{V=0}&= bd_II + u_1(t),\\ \left. \frac{dM}{dt}\right| _{M=0}&= s, \\ \left. \frac{dN}{dt}\right| _{N=0}&= \frac{p_3UM}{q_3 + U} + u_2(t), \end{aligned}$$

This proves that all the solutions of system (1)- (5) are positive for all \(t \ge 0\). \(\square \)

Theorem 2

(Boundedness) The solutions U(t), I(t), V(t), M(t), and N(t) of system (1)- (5) with positive initial conditions \(U_0, I_0, V_0\), \(M_0\), and \(N_0\) are bounded in the region

$$\begin{aligned} \Delta = \left\{ (U, I, M, V, N) \in \mathbb {R}_+^5: U(t) \le R, I(t) \le R, V(t) \le \frac{\mu _V}{d_V}, M(t) \le \frac{s}{d_M}, N(t) \le \frac{\mu _N}{d_N}\right\} . \end{aligned}$$

Proof

From Eqs. (1) and (2), we have

$$\begin{aligned} \frac{d(U+I)}{dt}= & {} \alpha U\left( 1 - \frac{U + I}{R}\right) - k_1MU - d_UU - k_2IM - d_II,\\ \frac{d(U+I)}{dt}\le & {} \alpha U\left( 1 - \frac{U + I}{R}\right) \le \alpha (U + I)\left( 1 - \frac{U + I}{R}\right) \le \alpha (U + I) - \mu _{T}(U + I)^2, \end{aligned}$$

where \(\mu _{T} = \frac{\alpha }{R}\). By using Bernoulli’s method, we have

$$\begin{aligned} U + I \le \frac{\alpha }{\mu _T + C\alpha e^{-\alpha t}}, \end{aligned}$$

with

$$\begin{aligned} C = \frac{\alpha - \mu _T(U_0+I_0)}{\alpha (U_0+I_0)}, \end{aligned}$$

and,

$$\begin{aligned} (U_0+I_0) = \frac{\alpha }{\mu _T + \alpha C}, \end{aligned}$$

and then,

$$\begin{aligned} \lim _{t\rightarrow \infty } \text {sup} \left[ U (T) + I(t)\right] \le \frac{\alpha }{\mu _T}, \end{aligned}$$

since \(U (T) + I(t) \le \frac{\alpha }{\mu _T} = R\), consequently \( U (T) \le R\), and \( I(t) \le R\).

From Eq. (3), we have

$$\begin{aligned} \frac{dV}{dt} = bd_II - \beta UV - d_V V - k_4MV + u_1 \le \mu _V - d_V V \end{aligned}$$

where, \(\mu _V = bd_IR + u_1\). By integrating, we have

$$\begin{aligned} V(t)\le & {} \frac{\mu _V}{d_V} + V_0e^{-d_Vt}\\ \lim _{t\rightarrow \infty } \text {sup} V(t)\le & {} \frac{\mu _V}{d_V}. \end{aligned}$$

From Eq. (4), we have

$$\begin{aligned} \frac{dM}{dt} = s + p_1(U+I)M + \frac{p_2MN}{q_2 + N} - k_3MU - d_MM \le s - d_MM, \end{aligned}$$

by integrating, we have

$$\begin{aligned} M\le & {} \frac{s}{d_M} + M_0e^{-d_Mt},\\ \lim _{t\rightarrow \infty } \text {sup} M(t)\le & {} \frac{s}{d_M}. \end{aligned}$$

From Eq. (5), we have

$$\begin{aligned} \frac{dN}{dt} = \frac{p_3UM}{q_3 + U} - d_NN + u_2 \le \mu _N - d_NN, \end{aligned}$$

where, \(\mu _N = \frac{s p_3R}{d_M(q_3 + R)} + u_2\). By integrating, we have

$$\begin{aligned} N(t)\le & {} \frac{\mu _N}{d_N} + N_0e^{-d_Nt},\\ \lim _{t\rightarrow \infty } \text {sup} N(t)\le & {} \frac{\mu _N}{d_N}. \end{aligned}$$

By all above, the solutions of system (1)–(5) are bounded. \(\square \)

3.2 Non-dimensionalization

To simplify the analysis of our system Eqs. (1)– (5), we begin by re-scaling them. For the re-scaling, we will use the following substitutions:

$$\begin{aligned} U = \hat{U} \bar{U},\quad I = \hat{I} \bar{I},\quad V = \hat{V} \bar{V}, \quad M = \hat{M} \bar{M}, \quad N = \hat{N} \bar{N}, \quad and \quad t = \hat{t} \bar{t}. \end{aligned}$$

The re-scaled system can be written as follows:

$$\begin{aligned} \frac{d\bar{U}}{d\bar{t}}= & {} \bar{U}\left( 1- \bar{U} -\bar{I}\right) - \phi _1\bar{U}\bar{V} - \phi _2\bar{U}\bar{M} - \phi _3\bar{U}, \end{aligned}$$
(6)
$$\begin{aligned} \frac{d\bar{I}}{d\bar{t}}= & {} \psi _1\bar{U}\bar{V} - \psi _2\bar{I}\bar{M} - \psi _3\bar{I}, \end{aligned}$$
(7)
$$\begin{aligned} \frac{d\bar{V}}{d\bar{t}}= & {} \bar{I} - \delta _1\bar{U}\bar{V} - \delta _2\bar{V} - \delta _3\bar{V}\bar{M} + \bar{u_1}, \end{aligned}$$
(8)
$$\begin{aligned} \frac{d\bar{M}}{d\bar{t}}= & {} 1 + \mu _1\bar{U}\bar{M} + \mu _2\bar{M}\bar{I} + \frac{\mu _3 \bar{M}\bar{N}}{ \mu _4 + \bar{N}} - \mu _5\bar{M}\bar{U} - \mu _6\bar{M}, \end{aligned}$$
(9)
$$\begin{aligned} \frac{d\bar{N}}{d\bar{t}}= & {} \frac{\bar{U}\bar{M}}{\chi _1 + \bar{U}} - \chi _2\bar{N} + \bar{u_2}, \end{aligned}$$
(10)

where

$$\begin{aligned} \hat{t}&= \frac{1}{\alpha },&\hat{U}&= R,&\hat{I}&= R,&\phi _1&= \frac{bd_IR\beta }{\alpha ^2},&\phi _2&= \frac{k_1s}{\alpha ^2}, \nonumber \\ \phi _3&= \frac{d_U}{\alpha },&\psi _1&= \frac{bd_IR\beta }{\alpha ^2},&\psi _2&= \frac{k_2s}{\alpha ^2},&\psi _3&= \frac{d_I}{\alpha },&\hat{V}&= \frac{bd_IR}{\alpha }, \nonumber \\ \delta _1&= \frac{R\beta }{\alpha },&\delta _2&= \frac{d_V}{\alpha },&\delta _3&= \frac{sk_4}{\alpha ^2},&\hat{M}&= \frac{s}{\alpha },&\mu _1&= \frac{p_1R}{\alpha }, \nonumber \\ \mu _2&= \frac{p_1R}{\alpha },&\mu _3&= \frac{p_2}{\alpha },&\mu _4&= \frac{q_2\alpha ^2}{sp_3},&\mu _5&= \frac{k_3R}{\alpha },&\mu _6&= \frac{d_M}{\alpha }, \nonumber \\ \hat{N}&= \frac{p_3s}{\alpha ^2},&\chi _1&= \frac{q_3}{R},&\chi _2&= \frac{d_N}{\alpha },&\bar{u_1}&= \frac{u_1}{bd_IR},&\bar{u_2}&= \frac{\alpha u_2}{p_3s}. \end{aligned}$$
(11)

3.3 The model without external doses

We obtain the model without external doses by setting \((\bar{u_1} = \bar{u_2} = 0)\) in the system (6)–(10). The new system will be written as follows:

$$\begin{aligned} \frac{d\bar{U}}{d\bar{t}}= & {} \bar{U}\left( 1- \bar{U} -\bar{I}\right) - \phi _1\bar{U}\bar{V} - \phi _2\bar{U}\bar{M} - \phi _3\bar{U}, \end{aligned}$$
(12)
$$\begin{aligned} \frac{d\bar{I}}{d\bar{t}}= & {} \psi _1\bar{U}\bar{V} - \psi _2\bar{I}\bar{M} - \psi _3\bar{I}, \end{aligned}$$
(13)
$$\begin{aligned} \frac{d\bar{V}}{d\bar{t}}= & {} \bar{I} - \delta _1\bar{U}\bar{V} - \delta _2\bar{V} - \delta _3\bar{V}\bar{M}, \end{aligned}$$
(14)
$$\begin{aligned} \frac{d\bar{M}}{d\bar{t}}= & {} 1 + \mu _1\bar{U}\bar{M} + \mu _2\bar{M}\bar{I} + \frac{\mu _3 \bar{M}\bar{N}}{ \mu _4 + \bar{N}} - \mu _5\bar{M}\bar{U} - \mu _6\bar{M}, \end{aligned}$$
(15)
$$\begin{aligned} \frac{d\bar{N}}{d\bar{t}}= & {} \frac{\bar{U}\bar{M}}{\chi _1 + \bar{U}} - \chi _2\bar{N}, \end{aligned}$$
(16)

3.3.1 Stability analysis of tumor-free equilibrium

We obtain the tumor-free equilibrium points by equating the right-hand side of Eqs. (12)–(16) to zero, with \(\bar{U} = \bar{I} = 0\). This results in the tumor-free equilibrium point \(E_{0}(\bar{U}^*, \bar{I}^*, \bar{V}^*\bar{M}^*, \bar{N}^*) = E_0(0,0,0,\frac{1}{\mu _6},0)\).

To linearize the system (12) - (16) around the equilibrium point, we must calculate the Jacobian matrix, which is given as follows:

$$\begin{aligned} J = \begin{pmatrix} \alpha _{11} &{} \alpha _{12} &{} \alpha _{13} &{} \alpha _{14} &{} 0 \\ \alpha _{21} &{} \alpha _{22} &{} \alpha _{23} &{} \alpha _{24} &{} 0 \\ \alpha _{31} &{} \alpha _{32} &{} \alpha _{33} &{} \alpha _{34} &{} 0 \\ \alpha _{41} &{} \alpha _{42} &{} 0 &{} \alpha _{44} &{} \alpha _{45} \\ \alpha _{51} &{} 0 &{} 0 &{} \alpha _{54} &{} \alpha _{55} \end{pmatrix}, \end{aligned}$$
(17)

where

$$\begin{aligned} \alpha _{11}&=1 - 2\bar{U} - \bar{I} - \phi _1\bar{V} - \phi _2 \bar{M} - \phi _3 , \qquad \qquad \alpha _{12} \qquad = - \bar{U} , \qquad \qquad \alpha _{13}=- \phi _1\bar{U}, \\ \alpha _{14}&= - \phi _2 \bar{U} , \qquad \qquad \qquad \alpha _{21} =\psi _1\bar{V} , \qquad \qquad \qquad \alpha _{22} =- \psi _2\bar{M} - \psi _3, \\ \alpha _{23}&=\psi _1\bar{U} , \qquad \qquad \qquad \alpha _{24} =- \psi _2 \bar{I} , \qquad \qquad \qquad \alpha _{31} =- \delta _1\bar{V} \\ \alpha _{32}&=1 ,\qquad \qquad \qquad \alpha _{33} = - \delta _1\bar{U} - \delta _2 - \delta _3\bar{M} , \qquad \qquad \qquad \alpha _{34} =- \delta _3\bar{V}, \\ \alpha _{41}&=\mu _1\bar{M} - \mu _5\bar{M} , \qquad \qquad \alpha _{42}=\mu _2\bar{M},\\ \alpha _{44}&=\mu _1\bar{U} + \mu _2\bar{I} + \frac{\mu _3\bar{N}}{\mu _4 + \bar{N}} -\mu _5\bar{U} - \mu _6, \quad \alpha _{45} =\frac{\mu _3\mu _4\bar{M}}{(\mu _4 + \bar{N})^2}, \quad \alpha _{51} =\frac{\chi _1\bar{M}}{(\chi _1 + \bar{U})^2}, \\ \alpha _{54}&=\frac{\bar{U}}{\chi _1 + \bar{U}}, \qquad \alpha _{55} =- \chi _2. \end{aligned}$$

The Jacobian matrix (17), around the equilibrium point \(E_{0}(0,0,0,\frac{1}{\mu _6},0)\) is given by:

$$\begin{aligned} J(E_0) = \begin{pmatrix} 1 - \frac{\phi _2}{\mu _6} - \phi _3 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} - \frac{\psi _2}{\mu _6} - \psi _3 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} - \delta _2 - \frac{\delta _3}{\mu _6} &{} 0 &{} 0 \\ \frac{\mu _1 - \mu _5}{\mu _6} &{} \frac{\mu _2}{\mu _6} &{} 0 &{} - \mu _6 &{} \frac{\mu _3}{\mu _4\mu _6 } \\ \frac{1}{\chi _1\mu _6} &{} 0 &{} 0 &{} 0 &{} - \chi _2 \end{pmatrix} , \end{aligned}$$
(18)

the eigenvalues of the matrix (18) are given by

$$\begin{aligned} \lambda _1 = 1 - \frac{\phi _2}{\mu _6} - \phi _3 ,\quad \lambda _2 = - \frac{\psi _2}{\mu _6} - \psi _3, \quad \lambda _3 = - \delta _2 - \frac{\delta _3}{\mu _6}, \quad \lambda _4 = - \mu _6, \quad \lambda _5 = - \chi _2. \end{aligned}$$

The tumor-free equilibrium point E\(_{0}\) is locally asymptotically stable if all the eigenvalues are negative or have negative real parts.

\(\lambda _2\), \(\lambda _3\), \(\lambda _4\), and \(\lambda _5\) are negatives. Additionally, \(\lambda _1\) is negative if and only if, \(\frac{\phi _2}{\mu _6} + \phi _3 > 1 \). This implies that the tumor-free \(E_{0}\) is stable if and only if \(k_1s + d_Ud_M > \alpha d_M \) otherwise, it is unstable.

Biological interpretation: The analysis of the tumor-free equilibrium point suggests that if the uninfected tumor cells’ growth rate \(\alpha \) is small and the killing rate \(k_1\) of the uninfected tumor cells by the immune cells is large, then small tumors can be entirely eliminated.

3.3.2 Stability analysis of endemic equilibrium

The endemic equilibrium points of the model (12)– (16), are \(E_i(\bar{U_i}^{**}, \bar{I_i}^{**}, \bar{V_i}^{**}, \bar{M_i}^{**}, \bar{N_i}^{**})\), \(i=1,2,3,...,n\) where \(E_i(\bar{U_i}^{**}, \bar{I_i}^{**}, \bar{V_i}^{**}, \bar{M_i}^{**}, \bar{N_i}^{**})\), are roots of

$$\begin{aligned}{} & {} \bar{U}\left[ 1- \bar{U} -\bar{I}\right] - \phi _1\bar{U}\bar{V} - \phi _2\bar{U}\bar{M} - \phi _3\bar{U} = 0, \end{aligned}$$
(19)
$$\begin{aligned}{} & {} \psi _1\bar{U}\bar{V} - \psi _2\bar{I}\bar{M} - \psi _3\bar{I} = 0, \end{aligned}$$
(20)
$$\begin{aligned}{} & {} \bar{I} - \delta _1\bar{U}\bar{V} - \delta _2\bar{V} - \delta _3\bar{V}\bar{M} = 0, \end{aligned}$$
(21)
$$\begin{aligned}{} & {} 1 + \mu _1\bar{U}\bar{M} + \mu _2\bar{M}\bar{I} + \frac{\mu _3 \bar{M}\bar{N}}{ \mu _4 + \bar{N}} - \mu _5\bar{M}\bar{U} - \mu _6\bar{M} = 0, \end{aligned}$$
(22)
$$\begin{aligned}{} & {} \frac{\bar{U}\bar{M}}{\chi _1 + \bar{U}} - \chi _2\bar{N} = 0. \end{aligned}$$
(23)

Finding equilibrium points for Eqs. (19)–(23), is challenging due to the nonlinearity and complexity of the equations, which are also parameter-dependent. To obtain these equilibrium points, we substitute parameter values from Table 1 into Eq. (11) to calculate the non-dimensionalized parameter values and then use these new values to solve Eqs. (19)–(23).

The Eqs. (19)–(23) yields four biologically meaningful equilibrium points. Among them, three are considered endemic equilibrium points, and they are as follows:

$$\begin{aligned} E_{1}(\bar{U_1}^{**}, \bar{I_1}^{**}, \bar{V_1}^{**}, \bar{M_1}^{**} \bar{N_1}^{**})&\approx E_{1}(0.00652, 0.00043, 0.000498, 0.000068, 0.000001), \end{aligned}$$
(24)
$$\begin{aligned} E_{2}(\bar{U_2}^{**}, \bar{I_2}^{**}, \bar{V_2}^{**}, \bar{M_2}^{**}, \bar{N_2}^{**})&\approx E_{2}(0.002464, 0, 0, 0.000167, 0.000002), \end{aligned}$$
(25)
$$\begin{aligned} E_{3}(\bar{U_3}^{**}, \bar{I_3}^{**}, \bar{V_3}^{**}, \bar{M_3}^{**}, \bar{N_3}^{**})&\approx E_{3}(0.512136, 0, 0, 0.000001, 0). \end{aligned}$$
(26)

Furthermore, there is a unique tumor-free equilibrium point:

$$\begin{aligned} E_{4}(\bar{U_4}^{**}, \bar{I_4}^{**},\bar{V_4}^{**} \bar{M_4}^{**},\bar{N_4}^{**}) \approx E_{4}(0, 0, 0, 20.576132, 0), \end{aligned}$$
(27)

which was previously investigated, and its stability was determined, when discussing the disease-free scenario. In this section, our attention will shift to the endemic equilibrium points.

The eigenvalues of the Jacobian matrix (17), around the endemic equilibrium point (24) are given by

$$\begin{aligned}{} & {} (\lambda _1, \lambda _2, \lambda _3, \lambda _4, \lambda _5) = (- 5388.61, - 48.5437, \\{} & {} - 5.70124, 0.23554 + 0.832952i, 0.23554 - 0.832952i), \end{aligned}$$

indicating that \(E_1\) is unstable as not all eigenvalues have negative real parts.

Similarly, for the endemic equilibrium point (25), the eigenvalues are:

$$\begin{aligned} (\lambda _1, \lambda _2, \lambda _3, \lambda _4, \lambda _5) = (-5981.14, -48.5437,-7.82967, -1.16393, 0.509646), \end{aligned}$$

\(E_2\) is also unstable since the eigenvalue \(\lambda _5\) is positive.

Finally, for the endemic equilibrium point (26), the eigenvalues are:

$$\begin{aligned} (\lambda _1, \lambda _2, \lambda _3, \lambda _4, \lambda _5) = (-1.24305\times 10^6, -48.5437, -34.5528, 7.11991, -0.509637), \end{aligned}$$

since the eigenvalue \(\lambda _4\) is not negative, this implies that E\(_3\) is unstable.

Biological interpretation: Analysis of these endemic equilibrium points suggests that virotherapy may have an impact on tumors. This impact could potentially lead to their eradication or, conversely, result in further tumor growth, as indicated by the instability of \(E_1, E_2\), and \(E_3\).

3.4 Stability analysis of model with external doses

In this part of the model analysis, we discuss the stability of the model (6)–(10) with external doses for both virotherapy and IL-2, namely \(\bar{u_1} \ne 0\) and \(\bar{u_2} \ne 0\). Our objective is to determine whether these injections can contribute to tumor eradication or not. We will examine the stability of both tumor-free and endemic cases.

3.4.1 Stability analysis of tumor-free equilibrium

We obtain the tumor-free equilibrium points by equating the right-hand side of Eqs. (6)–(10) to zero, with \(\bar{U} = \bar{I} = 0\). This results in the tumor-free equilibrium point \(F_{0}(\bar{U}^*, \bar{I}^*, \bar{V}^*\bar{M}^*, \bar{N}^*) = F_0(0,0,0,\frac{1}{\mu _6}, \frac{\bar{u_2}}{\chi _2})\).

To linearize the system (6)–(10) around the equilibrium point, we first calculate the Jacobian matrix, which is given as follows:

$$\begin{aligned} J = \begin{pmatrix} \alpha _{11} &{} \alpha _{12} &{} \alpha _{13} &{} \alpha _{14} &{} 0 \\ \alpha _{21} &{} \alpha _{22} &{} \alpha _{23} &{} \alpha _{24} &{} 0 \\ \alpha _{31} &{} \alpha _{32} &{} \alpha _{33} &{} \alpha _{34} &{} 0 \\ \alpha _{41} &{} \alpha _{42} &{} 0 &{} \alpha _{44} &{} \alpha _{45} \\ \alpha _{51} &{} 0 &{} 0 &{} \alpha _{54} &{} \alpha _{55} \end{pmatrix}, \end{aligned}$$
(28)

where

$$\begin{aligned} \alpha _{11}&=1 - 2\bar{U} - \bar{I} - \phi _1\bar{V} - \phi _2 \bar{M} - \phi _3 , \qquad \alpha _{12} = - \bar{U} , \qquad \alpha _{13} =- \phi _1\bar{U},\\ \alpha _{14}&= - \phi _2 \bar{U} , \qquad \alpha _{21} =\psi _1\bar{V} , \qquad \alpha _{22} =- \psi _2\bar{M} - \psi _3, \\ \alpha _{23}&=\psi _1\bar{U} , \qquad \alpha _{24}=- \psi _2 \bar{I} , \qquad \alpha _{31} =- \delta _1\bar{V}, \\ \alpha _{32}&=1 , \qquad \alpha _{33}= - \delta _1\bar{U} - \delta _2 - \delta _3\bar{M} , \qquad \alpha _{34} =- \delta _3\bar{V},\\ \alpha _{41}&=\mu _1\bar{M} - \mu _5\bar{M} , \qquad \alpha _{42} =\mu _2\bar{M},\\ \alpha _{44}&=\mu _1\bar{U} + \mu _2\bar{I} + \frac{\mu _3\bar{N}}{\mu _4 + \bar{N}} -\mu _5\bar{U} - \mu _6, \qquad \alpha _{45} =\frac{\mu _3\mu _4\bar{M}}{(\mu _4 + \bar{N})^2}, \\ \alpha _{51}&=\frac{\chi _1\bar{M}}{(\chi _1 + \bar{U})^2}, \qquad \alpha _{54} =\frac{\bar{U}}{\chi _1 + \bar{U}}, \qquad \alpha _{55} =- \chi _2. \end{aligned}$$

The Jacobian matrix (28), around the equilibrium point \(F_0(0,0,0,\frac{1}{\mu _6}, \frac{\bar{u_2}}{\chi _2})\) is given by:

$$\begin{aligned} J(F_0) = \begin{pmatrix} 1 - \frac{\phi _2}{\mu _6} - \phi _3 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} - \frac{\psi _2}{\mu _6} - \psi _3 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} - \delta _2 - \frac{\delta _3}{\mu _6} &{} 0 &{} 0 \\ \frac{\mu _1 - \mu _5}{\mu _6} &{} \frac{\mu _2}{\mu _6} &{} 0 &{} \frac{\mu _3\bar{u_2}}{\chi _2\mu _4 + \bar{u_2}} - \mu _6 &{} \frac{\mu _3\mu _4\chi _2^2}{\mu _6(\chi _2\mu _4 + \bar{u_2})^2} \\ \frac{1}{\chi _1\mu _6} &{} 0 &{} 0 &{} 0 &{} - \chi _2 \end{pmatrix}, \end{aligned}$$
(29)

the eigenvalues of the matrix (29) are given by

$$\begin{aligned} \lambda _1&= 1 - \frac{\phi _2}{\mu _6} - \phi _3 ,\qquad&\lambda _2&= - \frac{\psi _2}{\mu _6} - \psi _3, \qquad&\lambda _3&= - \delta _2 - \frac{\delta _3}{\mu _6}, \qquad \\ \lambda _4&= \frac{\mu _3\bar{u_2}}{\chi _2\mu _4 + \bar{u_2}} - \mu _6, \qquad&\lambda _5&= - \chi _2. \end{aligned}$$

\(\lambda _2\), \(\lambda _3\), and \(\lambda _5\) are negatives. Additionally, \(\lambda _1\) and \(\lambda _4\) are negative if and only if respectively, \(\frac{\phi _2}{\mu _6} + \phi _3 > 1 \) and \(\frac{\mu _3\bar{u_2}}{\chi _2\mu _4 + \bar{u_2}} < \mu _6\). This implies that the tumor-free \(F_{0}\) is stable if and only if

$$\begin{aligned} \frac{\mu _3\bar{u_2}}{\chi _2\mu _4 + \bar{u_2}}< \mu _6 < \phi _2 + \phi _3\mu _6, \end{aligned}$$
(30)

otherwise, it is unstable.

Biological interpretation: The analysis of the tumor-free equilibrium point suggests that the combination of virotherapy and IL-2 therapy could effectively eradicate tumors if \(\frac{\mu _3\bar{u_2}}{\chi _2\mu _4 + \bar{u_2}}< \mu _6 < \phi _2 + \phi _3\mu _6\). This condition implies that tumors can be eliminated when the natural death rate of immune cells (\(\mu _6\)) is less than the effective death rate of tumor cells. This effective rate is derived from the sum of the direct killing rate of tumor cells by immune cells (\(\phi _2\)) and the enhanced natural death rate of tumor cells influenced by the interaction with the natural death rate of immune cells (\(\phi _3\mu _6\)). This condition indicates that a lower death rate of immune cells, combined with their efficiency in killing tumor cells and the intrinsic vulnerability of tumor cells to die naturally, is crucial for eradicating tumors.

3.4.2 Stability analysis of endemic equilibrium

We determine the tumor-free equilibrium points by equating the right-hand side of Eqs. (6)–(10) to zero. Finding equilibrium points for Eqs. (6)–(10) is challenging due to the nonlinearity and complexity of the equations, which are also parameter-dependent. Again to obtain these equilibrium points, we substitute parameter values from Table 1 into Eq. (11) to calculate the non-dimensionalized parameter values and then use these new values to solve Eqs. (6)–(10), setting \(u_1 = 300\) and \(u_2 = 2 \times 10^4\).

The system (6)–(10) yields two biologically meaningful endemic equilibrium points, given by

$$\begin{aligned} F_1(\bar{U_1}^{**}, \bar{I_1}^{**}, \bar{V_1}^{**} ,\bar{M_1}^{**} \bar{N_1}^{**})&\approx F_1(0.00622, 0.00092, 0.00120, 0.00008, 0.00131), \end{aligned}$$
(31)
$$\begin{aligned} F_2(\bar{U_2}^{**}, \bar{I_2}^{**}, \bar{V_2}^{**}, \bar{M_2}^{**} \bar{N_2}^{**})&\approx F_2 (0.001384,0.000006, 0.000080, 0.000299, 0.001309). \end{aligned}$$
(32)

The stability of the endemic equilibrium point \(F_1\) is confirmed by its eigenvalues:

$$\begin{aligned}{} & {} (\lambda _1, \lambda _2, \lambda _3, \lambda _4, \lambda _5) = \\{} & {} \quad (-12870.7, -48.5437, -5.98862, -0.194163 + 0.961903 i, -0.194163 - 0.961903 i), \end{aligned}$$

indicating that \(F_1\) is stable since all eigenvalues are negative.

Conversely, the eigenvalues associated with the endemic equilibrium point \(F_2\) are:

$$\begin{aligned} (\lambda _1, \lambda _2, \lambda _3, \lambda _4, \lambda _5) = (-3345.88, -48.5437, -11.7514, -2.19149, 0.416727), \end{aligned}$$

demonstrating instability in \(F_2\) due to the presence of a positive eigenvalue.

Biological interpretation: Analysis of these endemic equilibrium points suggests that while virotherapy combined with IL-2 therapy may not effectively eradicate larger tumors \((\bar{U_1}^{**} = 0.00622)\), as indicated by the stability of \(F_1\), it may have a significant impact on smaller tumors \((\bar{U_2}^{**} = 0.001384)\). This impact could potentially lead to their eradication or, conversely, result in further tumor growth, as indicated by the instability of \(F_2\). These findings highlight the critical importance of tumor size in treatment efficacy and emphasize the complex dynamics between the tumor and the immune system.

4 Uncertainty and sensitivity analysis

In this section, we investigate the impact of model (1)– (5) parameters on the model outputs, namely tumor cell dynamics. Our goal is to determine which parameters most significantly impact the proliferation and inhibition of tumor cells. To assess the uncertainty and sensitivity of these parameters, we utilized Latin hypercube sampling (LHS) and analyzed their impacts using the partial rank correlation coefficient (PRCC) method, following the methodology presented by Marino et al. [65].

The parameters range in Table 1 were set from 1/10 to twice their baseline values. We selected a sample size of 100, in line with the recommendation by Marino et al. [65]. We employed LHS to calculate the PRCC and their associated p-values with respect to the tumor cell population (U + I), as presented in Figures 2, 3, 4, and 5. The PRCC values range between \(-1\) and \(+1\), signify the degree of correlation between a parameter and the tumor cell population. The positive and negative values of PRCC indicate a positive and negative correlation, respectively. A PRCC value of zero implies no significant correlation. Furthermore, PRCC values close to either \(+1\) or \(-1\) suggest a strong positive and negative correlation. In contrast, the values close to zero indicate a weak correlation.

Figure 2 shows the PRCC plot for the same parameters, using a significance level of 0.05 at time \(t = 7\). Figure 2 indicates that the growth rate of the uninfected tumor cells, \(\alpha \); the infection rate, \(\beta \); the burst size, b; and the killing rate of the immune cells by the uninfected cells, \(k_3\), are sensitive to tumor cell growth, with p-values \(< 0.05\). Thus, the parameters \(\beta \) and b display negative impacts on the tumor cell population, implying that an increase in any of these parameters leads to a decrease in the tumor cell population and vice versa. On the other hand, the parameters \(\alpha \) and \(k_3\) have positive impacts on the tumor cell population, suggesting that an increase in the growth rate of the uninfected tumor cells and the killing rate of immune cells by the uninfected cells results in an increase in the tumor cell population and vice versa.

Figure 4 displays the PRCC plot for the parameters in Table 1, with a significance level of 0.05 at time \(t = 20\). It reveals that the growth rate of the uninfected cells, \(\alpha \); the infection rate, \(\beta \); the killing rate of the uninfected cells by the immune cells, \(k_1\); and the burst size, b, are sensitive to the growth of the tumor cell population with a p-value \(< 0.05\). The growth rate of the uninfected cells, \(\alpha \), has a significant positive impact on the tumor cell population, indicating a positive correlation. In other words, an increase in the growth rate of the uninfected cells leads to an increase in the tumor cell population and vice versa. Conversely, the parameters \(\beta \), \(k_1\), and b exhibit negative impacts on the tumor cell population, indicating a negative correlation. This implies that an increase in any of these parameters decreases the tumor cell population and vice versa.

Fig. 2
figure 2

PRCCs results demonstrate the correlation between total tumor cell population and model parameters at time t = 7 with a significant level of 0.05. The most sensitive parameters are \(\alpha \), \(\beta \), b, and \(k_3\), (p-values are less than 0.05)

Full size image
Fig. 3
figure 3

PRCC scatter plots for the most significant parameters \((\alpha , \beta , b, and k_3)\), computed at a significance level of 0.05 at the time point \(t = 7\). Each plot’s title displays the PRCC value along with the corresponding p-value.

Full size image

At both \(t=7\) and \(t=20\), it is evident that the burst size of infected tumor cells is the most influential parameter, negatively affecting the tumor cell population. Therefore, this implies that an increase in the burst size of infected tumor cells results in a significant decrease in the tumor cell population.

We utilized LHS to plot PRCC scatter plots for all parameters. However, in this paper, we introduce and discuss only the most significant parameters. These scatter plots are crucial for illustrating the relationships between model variables and parameters, as determined by PRCC analysis. Figure 3 depicts scatter plots for the parameters \(\alpha \), \(\beta \), b, and \(k_3\), at a significance level of 0.05 at time \(t=7\). Notably, the killing rate of immune cells by the uninfected tumor cells, \(k_3\), exhibits the most significant positive correlation with the total tumor cell population, showing a PRCC of 0.63479 and a small p-value of \(1.32 \times 10^{-12}\), which is well below the significance level of 0.05. Conversely, the burst size, b, demonstrates the most significant negative correlation with the total tumor cell population, with a PRCC of \(-0.58352\) and an extremely small p-value of \(1.8742 \times 10^{-10}\).

Figure 5 displays PRCC scatter plots for \(\alpha \), \(\beta \), \(k_1\), and b, with a significance level of 0.05 at time \(t=20\). Here, the growth rate of the uninfected tumor cells, \(\alpha \), shows the most significant positive correlation with the total tumor cell population, with a PRCC of 0.32632 and a p-value of 0.00092196, below the significance level of 0.05. The burst size, b, again shows a significant negative correlation, with a PRCC of \(-0.43235\) and a p-value of \(7.0542 \times 10^{-6}\).

Fig. 4
figure 4

PRCCs results demonstrate the correlation between total tumor cells population and model parameters at time t = 20 with a significant level of 0.05. The most sensitive parameters are \(\alpha \), \(\beta \), \(k_1\), and b, (p-values are less than 0.05)

Full size image
Fig. 5
figure 5

PRCC scatter plots for the most significant parameters \((\alpha , \beta , b, and~k_1)\), computed at a significance level of 0.05 at the time point \(t = 20\). Each plot’s title displays the PRCC value along with the corresponding p-value.

Full size image

5 Optimal control analysis

In this section, we explore the existence and necessary conditions for the optimal control. Our aim is to minimize the total number of infected and uninfected tumor cells by the end of the treatment period, along with minimizing the dose of administered drugs to reduce potential drug-induced toxicity. To achieve this goal, we formulated the objective function as follows:

$$\begin{aligned} J(u_1, u_2) = \int _{0}^{t_f} \left[ AU(t) + BI(t) + \frac{1}{2}C_1u_1^2(t) + \frac{1}{2}C_2u_2^2(t) \right] dt, \end{aligned}$$
(33)

where coefficients A and B are balancing coefficients associated with the cost of clearing uninfected tumor cells and infected tumor cells, while coefficients C\(_1\) and C\(_2\) are associated with the cost of implementing virotherapy and IL-2, respectively. \(t_f\) represents the termination time of the treatment. The optimal combination of control variables \(u_1\) and \(u_2\) will be adequate to minimize the concentration of tumor cells and the negative side effects over a fixed period. The first two terms of the integrand function represent the concentrations of uninfected and infected tumor cells, respectively, while the latter two represent the effectiveness of the applied treatment. In this context, we employ an optimal control problem related to the model to minimize virotherapy and IL-2 administration, aiming to reduce side effects.

We made the assumption that the control variables \(u_1\) and \(u_2\) are bounded and Lebesgue integrable. Consequently, we aim to find an optimal control pair \((u_1^*, u_2^*)\) \(\in \) \(\Omega \), which minimizes the objective function (33), where

$$\begin{aligned} \Omega = \left\{ u_1, u_2: u_1^{Min} \le u_1 \le u_1^{Max}, u_2^{Min} \le u_2 \le u_2^{Max}, t \in [0, t_f] \right\} , \end{aligned}$$
(34)

represents the set of admissible controls, where \(u_1(t) = u_1^{Max}\) and \(u_2(t) = u_2^{Max}\) indicate the maximum administration of virotherapy and IL-2 treatments, respectively, while \(u_1(t) = u_1^{Min}\) and \(u_2(t) = u_2^{Min}\) indicate the minimum administration of these treatments, respectively.

In the next subsection, we discuss the existence of the optimal control solution, but before that, we need to first show that the solutions of the system (1)- (5) are bounded for a finite time period (finite time interval). This means to determine the upper bounds (super-solutions) of U, I, V, M, and N in the system (1)– (5). The sub-solutions are zero. From system (1)– (5), we have \(\frac{U}{dt}< \alpha U, \frac{dI}{dt}< \beta UV, \frac{dV}{dt}< bd_II + u_1, \frac{dM}{dt}< s + p_1(U+I)M + p_2M\), and \(\frac{dN}{dt} < p_3M + u_2\). If \(U_m\) is the upper bound of the solution U, then \(U_m = U_0e^{\alpha t_f}\). Similarly if \(I_m, V_m, M_m\) and \(N_m\) are upper bounds of U, V, M, and N respectively, then we have,

$$\begin{aligned} I_m&= (\beta U_mV_m)t_f + I_0 \qquad , V_m = (bd_II_m + u_1)t_f + V_0, \\ M_m&= e^{(p_1(U+I)+p_2)t_f}\left[ \frac{-s}{p_1(U+I)+p_2}\left( e^{-(p_1(U+I)+p_2)t_f} - 1\right) + M_0\right] , \\ \text {and}\\ N_m&= (p_3M_m + u_2)t_f + N_0, \end{aligned}$$

if we denoted to these upper pounds by \(\bar{U}, \bar{I}, \bar{V}, \bar{M}\), and \(\bar{N}\), then we have the following system

$$\begin{aligned} \frac{d\bar{U}}{dt}= & {} \alpha \bar{U}, \end{aligned}$$
(35)
$$\begin{aligned} \frac{d\bar{I}}{dt}= & {} \beta U_mV_m,\end{aligned}$$
(36)
$$\begin{aligned} \frac{d\bar{V}}{dt}= & {} bd_II_m + u_1,\end{aligned}$$
(37)
$$\begin{aligned} \frac{d\bar{M}}{dt}= & {} s + p_1(U_m+I_m)\bar{M} + p_2\bar{M},\end{aligned}$$
(38)
$$\begin{aligned} \frac{d\bar{N}}{dt}= & {} p_3M_m + u_2, \end{aligned}$$
(39)

that is bounded by a finite time interval.

5.1 Existence of the optimal control solution

In this subsection, we will discuss the existence of the optimal control of our system (1)– (5). We will show this using the following theorem.

Theorem 3

Given the objective functional in (33), where

$$\begin{aligned} \Omega = \left\{ \vec {u}(t), \text {Lebesguemeasure} : \vec {u}_{Min}(t) \le \vec {u}(t) \le \vec {u}_{Max}(t), t \in [0, t_f] \right\} . \end{aligned}$$
(40)

subject to system (1)– (5) with \(U(0) = U_0, I(0) = I_0, V(0) = V_0, M(0) = M_0\), and \(N(0) = N_0\), then there exists an optimal control \(\vec {u^*}\) such that \(\text {min}_{\vec {u^*}(t) \in [\vec {u}_{Min}, \vec {u}_{Max}]} J(\vec {u})\) = \(J(\vec {u^*})\) if the following conditions hold

  1. 1.

    f is not empty.

  2. 2.

    The admissible control set \(\Omega \) is closed and convex.

  3. 3.

    Each right-hand side of the state system is continuous, is bounded above by the sum of the bounded control and the state and can be written as a linear function of \(\vec {u}\) with coefficients depending on time and the state.

  4. 4.

    The integrand of \(J(\vec {u})\) is convex on \(\Omega \) and is bounded below by \(- c_2 + c_1\vec {u^2}\) with \(c_1 > 0\).

Proof

Since the system (1)- (5) has bounded coefficients and the solutions are bounded on the finite time interval, we can apply the result of Lukes [66] (theorem 9.2.1, P.182) to obtain the existence of the solution of the system (1)- (5). Furthermore, we note that \(\Omega \) is closed and convex by definition. For the third condition, the right-hand side of the system (1)- (5) must be continuous. There may be instances where discontinuity occurs solely in the right-hand side of \(\frac{dU}{dt}\) due to changes in the term \(\frac{U+I}{R}\) and in \(\frac{dM}{dt}\) due to the term \(\frac{p_2MN}{q_2 + N}\). However, since R, \(q_2\) and N are all positive, this eliminates the possibility of undefined values for \(\frac{U+I}{R}\) and \(\frac{p_2MN}{q_2 + N}\), as \(q_2 + N\) is also positive. Thus, the entire system remains continuous.

We set \(\vec {\phi }(t, \vec {X})\) be the right-hand side of system (1)- (5) except for the terms of \(\vec {u}\) and define

$$\begin{aligned} \vec {f}(t, \vec {X}, \vec {u^*}) = \vec {\phi }(t, \vec {X}) + \begin{pmatrix} 0 \\ 0 \\ u_1 \\ 0 \\ u_2 \end{pmatrix}, \qquad \text {with} \hspace{0.3cm} \vec {X} = \begin{pmatrix} U \\ I \\ V \\ M \\ N \end{pmatrix}. \end{aligned}$$

where \(\vec {\phi }\) is a vector valued function of \(\vec {X}\). Using the boundedness of the solutions, we have

$$\begin{aligned} \begin{aligned} \left| \vec {f}(t, \vec {X}, \vec {u^*} )\right|&\le \left| \begin{pmatrix} \alpha &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0&{} \beta U_m &{} 0 &{} 0 \\ 0 &{} bd_I &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} p_1(U_m+I_m) + p_2 &{} 0 \\ 0 &{} 0 &{} 0 &{} p_3M &{} 0 \end{pmatrix} \begin{pmatrix} U \\ I \\ V \\ M \\ N \end{pmatrix} \right| + \left| \begin{pmatrix} 0 \\ 0 \\ u_1 \\ s \\ u_2 \end{pmatrix}\right| \\&\le c_1\left( \left| \vec {X} \right| , \left| \vec {u^*} \right| \right) , \end{aligned} \end{aligned}$$

where \(c_1\) depends on the coefficients of the system.

For the fourth condition, we need to show that

$$\begin{aligned} J(t, U, I, (1-P)\vec {u} + Pw) \le (1-P)J(t, U, I, \vec {u}) + PJ(t, U, I, w), \end{aligned}$$

where \(J(t, U, I, \vec {u}) = AU(t) + BI(t) + \frac{1}{2}C_1u_1^2(t) + \frac{1}{2}C_2u_2^2(t) \).

we analyze the difference of

$$\begin{aligned} \begin{aligned}&J(t, U, I, (1-P)\vec {u} + Pw) - \left( (1-P)J(t, U, I, \vec {u}) + PJ(t, U, I, w) \right) \\&= AU + BI + \frac{C_i}{2}\left( \vec {u}^2 - 2P\vec {u}^2 + P^2\vec {u}^2 + 2P\vec {u}w - 2\vec {u}wP^2 + P^2w^2\right) \\&- \left( AU + BI + \frac{C_i}{2}\vec {u}^2 - \frac{C_i}{2}P\vec {u}^2 + \frac{C_i}{2}P\vec {w}^2\right) \\&= \frac{C_i}{2}\left( P^2 - P\right) \left( \vec {u} - w\right) ^2, \end{aligned} \end{aligned}$$

since \(P\in (0, 1)\), it follows that \(\left( P^2 - P\right) < 0\) and \(\left( \vec {u} - w\right) ^2 > 0\), which in turn implies that \(\frac{C_i}{2}\left( P^2 - P\right) \left( \vec {u} - w\right) ^2\) is negative. Consequently, we have

$$\begin{aligned} J(t, U, I, (1-P)\vec {u} + Pw) \le (1-P)J(t, U, I, \vec {u}) + PJ(t, U, I, w). \end{aligned}$$

Lastly

$$\begin{aligned} AU + BI + \frac{C_i}{2}\vec {u}^2 \ge \frac{C_i}{2}\vec {u}^2 \ge - c + \frac{C_i}{2}\vec {u}^2, \end{aligned}$$

which gives \(- c + \frac{C_i}{2}\vec {u}^2\) as the lower bound. \(\square \)

5.2 Necessary conditions for optimality

To determine the necessary conditions for our optimal control, we use Pontriagin’s Maximum Principle [67]. To apply this principle, we first need to define the problem’s Hamiltonian  [68]. The Hamiltonian for the optimal control problem (33) and  (1)– (5), is given by:

$$\begin{aligned} H&= AU(t) + BI(t) + \frac{1}{2}C_1u_1^2(t) + \frac{1}{2}C_2u_2^2(t) \\&\quad + \lambda _1 \left[ \alpha U\left( 1 - \frac{U + I}{R}\right) - \beta UV - k_1MU - d_UU \right] \\&\quad + \lambda _2 \left[ \beta UV - k_2IM - d_II \right] \\&\quad + \lambda _3\left[ bd_II - \beta UV - d_V V - k_4 VM + u_1(t) \right] \\&\quad + \lambda _4 \left[ s + p_1(U+I)M + \frac{p_2MN}{q_2 + N} - k_3MU - d_MM \right] \\&\quad + \lambda _5 \left[ \frac{p_3UM}{q_3 + U} - d_NN + u_2(t) \right] , \end{aligned}$$

where \(\lambda _i, 1 \le i \le 5\) are co-state variables satisfying the equations

$$\begin{aligned} \frac{d\lambda _1}{dt}&= - \frac{dH}{dU} = - \left( A + \lambda _1\left[ \alpha - \frac{2\alpha U}{R} - \frac{\alpha I}{R} - \beta V - k_1M - d_U \right] + \lambda _2\beta V - \lambda _3 \beta V \right) \nonumber \\&\quad - \lambda _4(p_1M - k_3M) - \frac{\lambda _5p_3q_3M}{(q_3 + U)^2}, \end{aligned}$$
(41)
$$\begin{aligned} \frac{d\lambda _2}{dt}&= - \frac{dH}{dI} = - \left( B - \frac{\lambda _1\alpha U}{R} - \lambda _2(k_2M + d_I) + \lambda _3bd_I + \lambda _4p_1M \right) , \end{aligned}$$
(42)
$$\begin{aligned} \frac{d\lambda _3}{dt}&= - \frac{dH}{dV} = - \left( - \lambda _1\beta U + \lambda _2\beta U - \lambda _3(\beta U + d_V + k_4M) \right) ,\end{aligned}$$
(43)
$$\begin{aligned} \frac{d\lambda _4}{dt}&= - \frac{dH}{dM} = - \left( - \lambda _1k_1U - \lambda _2k_2I - \lambda _3k_4V \right. \nonumber \\&\quad \left. + \lambda _4\left[ p_1(U + I) + \frac{p_2N}{q_2 + N} - k_3U - d_M\right] \right) - \left( \frac{\lambda _5p_3U}{q_3 + U} \right) ,\end{aligned}$$
(44)
$$\begin{aligned} \frac{d\lambda _5}{dt}&= - \frac{dH}{dN} = - \left( \frac{\lambda _4p_2q_2M}{(q_2 + N)^2} - \lambda _5d_N \right) , \end{aligned}$$
(45)

with transversality conditions

$$\begin{aligned} \lambda _1(t_f) = \lambda _2(t_f) = \lambda _3(t_f) = \lambda _4(t_f) = \lambda _5(t_f) = 0. \end{aligned}$$
(46)

The optimal controls \((u_1^*, u_2^*)\) \(\in \) \(U\times U\) minimizing the Hamiltonian are obtained by solving the equations

$$\begin{aligned} \frac{\partial H}{\partial u_1}&= C_1u_1 + \lambda _3 = 0,\nonumber \\ \text {and}\end{aligned}$$
(47)
$$\begin{aligned} \frac{\partial H}{\partial u_2}&= C_2u_2 + \lambda _5 = 0, \end{aligned}$$
(48)

consequently,

$$\begin{aligned} {u_1}^*&= - \frac{\lambda _3}{C_1} {}, \text {and}\end{aligned}$$
(49)
$$\begin{aligned} {u_2}^*&= - \frac{\lambda _5}{C_2} {}, \end{aligned}$$
(50)

Imposing the constraints \(u_1^{Min} \le u_1 \le u_1^{Max}\) and \(u_2^{Min} \le u_2 \le u_2^{Max}\), gives

$$\begin{aligned} {u_1}^*= & {} {\left\{ \begin{array}{ll} - \frac{\lambda _3}{C_1}, \hspace{0.3cm} \text {if} \hspace{0.3cm} u_1^{Min}< - \frac{\lambda _3}{C_1} < u_1^{Max}, \\ u_1^{Min}, \hspace{0.3cm} \text {if} \hspace{0.3cm} - \frac{\lambda _3}{C_1} \le u_1^{Min}, \\ u_1^{Max}, \hspace{0.3cm} \text {if} \hspace{0.3cm} - \frac{\lambda _3}{C_1} \ge u_1^{Max}. \end{array}\right. }\nonumber \\ \text {and}\end{aligned}$$
(51)
$$\begin{aligned} {u_1}^*= & {} {\left\{ \begin{array}{ll} - \frac{\lambda _5}{C_2}, \hspace{0.3cm} \text {if} \hspace{0.3cm} u_1^{Min}< - \frac{\lambda _5}{C_2} < u_2^{Max}, \\ u_2^{Min}, \hspace{0.3cm} \text {if} \hspace{0.3cm} - \frac{\lambda _5}{C_2} \le u_2^{Min}, \\ u_2^{Max}, \hspace{0.3cm} \text {if} \hspace{0.3cm} - \frac{\lambda _5}{C_2} \ge u_2^{Max}. \end{array}\right. } \end{aligned}$$
(52)

in compact notation, the optimal controls are characterized by the following:

$$\begin{aligned} {u_1}^*= & {} \text {min}\left\{ \text {max}\left( u_1^{Min}, - \frac{\lambda _3}{C_1}\right) , u_1^{Max}\right\} ,\nonumber \\ \text {and}\end{aligned}$$
(53)
$$\begin{aligned} {u_2}^*= & {} \text {min}\left\{ \text {max}\left( u_2^{Min}, - \frac{\lambda _5}{C_2}\right) , u_2^{Max}\right\} , \end{aligned}$$
(54)

In the next section, we will discuss the numerical solutions to our optimal control problem and the treatment strategies we will follow to effectively eradicate cancer.

Fig. 6
figure 6

The plots depict the effect of continuous infusion of virotherapy on the populations of uninfected tumor cells, infected tumor cells, OVs, and total tumor cells. They show that tumors can be eradicated through virotherapy alone. We set \(u_1 = 150\) PUF and \(u_2 = 0\). The initial conditions are \(U(0) = 1 \times 10^5, I(0) = 2 \times 10^3, V(0) = 1 \times 10^3, M(0) = 2 \times 10^3, and N(0) = 5 \times 10^2.\) All other parameters are kept constant with the values provided in Table (1)

Full size image
Fig. 7
figure 7

The plots depict the effects of continuous infusion of combined virotherapy and IL-2 on the populations of uninfected tumor cells, infected tumor cells, OVs, and total tumor cells. They demonstrate that tumors can be eradicated effectively when virotherapy is combined with IL-2. We fixed \(u_1 = 150\) PUF and \(u_2 = 10000\) IU. The initial conditions are \(U(0) = 1 \times 10^5, I(0) = 2 \times 10^3, V(0) = 1 \times 10^3, M(0) = 2 \times 10^3, and N(0) = 5 \times 10^2.\) All other parameters are kept constant with the values provided in Table (1)

Full size image
Fig. 8
figure 8

The plots show the effects of varying burst size rates on the populations of uninfected tumor cells, OVs, infected tumor cells, and total tumor cells. Increasing the burst size rates leads to a decrease in the densities of uninfected, infected, and total tumor cells, while simultaneously increasing the density of free viruses. We set \(u_1 = 150\) PFU and \(u_2 = 10000\) IU. The initial conditions are \(U(0) = 1 \times 10^5\), \(I(0) = 2 \times 10^3\), \(V(0) = 1 \times 10^3\), \(M(0) = 2 \times 10^3\), and \(N(0) = 5 \times 10^2\). Other parameters are kept at their values given in Table (1)

Full size image

6 Numerical simulations

In this section, we discuss the numerical simulations of the system (1)– (5). First, we obtain the numerical solution through a continuous treatment without control for different burst size values, as detailed in the first subsection (6.1). Following that, the second subsection (6.2) explores the numerical solutions under treatment control.

For the optimal control solutions, we utilized the forward-backward method to find the optimal control solution by solving the optimality systems (1)– (5) and (41)-(45). We start by solving the state system (1)- (5) forward in time using an initial guess for the controls \((u_1, u_2)\). Using the transversality conditions (46), we solve the costate system (41)-(45) backward in time.

The parameters used in the numerical simulations are the same parameters in Table 1. The initial values for the state variables of the model used in the numerical simulations are as follows: \(U(0) = 1 \times 10^5\), \(I(0) = 2 \times 10^3\), \(V(0) = 1 \times 10^3\), \(M(0) = 2 \times 10^3\), and \(N(0) = 5 \times 10^2\). The weights are given by, \(A = 1 \times {10}^{-6}\), \(B = 1 \times {10}^{-5}\), \(C_1 = 1\times 10^{-10}\), and \(C_2 = 1 \times 10^{-10}\).

Fig. 9
figure 9

The plots show the effects of varying infection rates on the populations of uninfected tumor cells, OVs, and infected tumor cells. Increasing the infection rates leads to a decrease in the density of uninfected tumor cells, a decrease in free virus density, and an increase in the density of infected tumor cells. We set \(u_1 = 150\) PFU and \(u_2 = 10000\) IU. The initial conditions are \(U(0) = 1 \times 10^5, I(0) = 2 \times 10^3, V(0) = 1 \times 10^3, M(0) = 2 \times 10^3, and N(0) = 5 \times 10^2\) . All other parameters are kept constant with the values provided in Table 1

Full size image

6.1 Drug infusion without control

Figures 6 and 7 respectively show the effects of virotherapy alone and its combination with IL-2 on the populations of uninfected tumor cells, infected tumor cells, OVs, and total tumor cells (including both infected and uninfected tumor cells). They show that virotherapy is capable of eradicating the tumor, but it will give better results when combined with IL-2. From Fig. 6a, we observe oscillations in the population of uninfected tumor cells when virotherapy is used alone. However, this oscillation is reduced when virotherapy is combined with IL-2, as depicted in Fig. 7a.

Figure 8, shows the populations of uninfected tumor cells, OVs, infected tumor cells, and the total tumor cells with different burst sizes. In Fig. 8a, we observe how an increase in burst size reduces the time required for uninfected tumor cells to reach very low levels, even when other parameters remain constant. For example, when the burst size (b) is set to 1.5, uninfected tumor cells require almost 30 days to reach their low levels. However, this duration was decreased to almost 20 days when the burst size was increased to \(b = 2\). However, this observation indicates the important role of burst size in reducing tumor cells, as discussed during the sensitivity analysis. This effect is further confirmed by Fig. 8c and d, where both infected tumor cells and total tumor cells density (including infected and uninfected tumor cells) decrease to very low levels with an increase in burst size.

Figure 9 shows the populations of uninfected tumor cells, infected tumor cells, OVs, and total tumor cells under different infection rates. It shows that increasing the infection rate results in a decrease in the densities of the uninfected tumor cells and the OVs while increasing the density of the infected tumor.

Figure 9a shows that at a lower infection rate of \(\beta = 1 \times 10^{-6}\), uninfected tumor cells decrease to a low density over a period of 20 days. Conversely, with a higher infection rate of \(\beta = 9 \times 10^{-5}\), the uninfected tumor cells decrease to a low density within just one week, as indicated in Fig. 9d. At the same time, the density of OVs at \(\beta = 1 \times 10^{-6}\) reaches its maximum at nearly \(5 \times 10^{5}\), but decreases to about \(2 \times 10^{4}\) when the infection rate increases to \(\beta = 9 \times 10^{-5}\). Furthermore, the density of infected tumor cells exhibits a slight increase from \(5 \times 10^{4}\) at the lower infection rate to \(4.5 \times 10^{5}\) at the higher rate, as shown in Fig. 9a and d, respectively.

Fig. 10
figure 10

The plot represents the densities of uninfected tumor cells, infected tumor cells, virotherapy input, and IL-2 input. The results show the successful elimination of both uninfected and infected tumor cells

Full size image

6.2 Drug infusion under control

Figures 10a, , 11, 10c, and d show densities and concentrations of uninfected tumor cells, infected tumor cells, total tumor cells, virotherapy input, and IL-2 input, respectively. We notice that tumor cells are eliminated in less than 10 days of treatment. We can come to a conclusion that the optimal doses of \(u_1 = 100\) PUF and \(u_2 = 5000\) IU are sufficient to eliminate the tumor entirely.

Fig. 11
figure 11

The plot shows the total tumor cell population under virotherapy and IL-2 controls

Full size image

7 Conclusion

In this study, we developed and analyzed a mathematical model describing the interactions between uninfected tumor cells, infected tumor cells, immune cells, and oncolytic virotherapy in combination with immunotherapy. Our main aim was to investigate the potential of this combination to enhance treatment outcomes. We started the model analysis by establishing the positivity and boundedness of the system solutions. To simplify the system analysis, we re-scaled our model system. We explored equilibrium points and conducted stability analysis for both tumor-free and endemic cases. The tumor-free equilibrium points demonstrated stability under specific conditions in scenarios both with and without external doses. In contrast, the endemic equilibrium points behaved differently. Without external doses, these points exhibited instability. However, when external doses were incorporated into the model, one of the endemic equilibrium points remained unstable, while the other exhibited stability. The stability of these tumor-free equilibrium points suggests that the immune system is capable of eliminating all uninfected tumor cells, infected tumor cells, and viruses. These findings align with previous studies by Vithanage et al. [40] and Vithanage et al. [41].

We conducted a sensitivity analysis using Latin hypercube sampling (LHS) to identify key parameters contributing to cancer eradication during treatment. This analysis, performed at two different time points, highlighted the critical role of the burst size of infected tumor cells. Numerical simulations were conducted for the model under continuous infusion of virotherapy and IL-2. The results indicated that virotherapy alone might be capable of eradicating tumors, as shown in Fig. 6. Furthermore, combining virotherapy with IL-2 showed enhanced results, as depicted in Fig. 7.

By employing Pontryagin’s Maximum Principle, we solved the optimal control problem. Numerical simulations for optimal control problems were conducted to identify the optimal dose profile to minimize tumor size, as well as the administered treatment. The simulation results demonstrated the success of combined virotherapy and immunotherapy in eliminating tumors, as depicted in Fig. 10.

This result is in line with a previous study given by Aghbash et al. [69], which demonstrated promising results in using IL-2 to stimulate immune responses in tumor-virotherapy microenvironments across various types of cancer.