1 Introduction

In history, mankind has witnessed several global epidemics of infectious diseases. These infectious diseases, without exception, have brought serious threats to the safety of human life and property, and even caused a huge impact on society and the regime. Typical cases include the smallpox outbreak in Europe in the 18th century [1], the Spanish flu in 1918 [2], and the COVID-2019, which is ravaging the world [3]. The prevention and control of emerging infectious diseases has become a hot issue of global concern. Although scientists from different fields have devoted themselves to the research related to the prevention and control of infectious diseases and have achieved many remarkable results, the research related to the transmission dynamics of infectious diseases is still in its infancy, and there are many important challenges to be solved urgently [4, 5].

The intervention of mathematical models brings a new perspective to the study of the transmission mechanism of infectious diseases [6]. Mathematical models of infectious diseases date back to the work of Daniel Bernoulli in 1760, who predicted that universal vaccination against smallpox would increase average life expectancy by more than three years [7]. In 1911, Ronald Ross was awarded the Nobel Prize in Medicine for his work on the transmission of malaria between mosquitoes and humans, the first time in history that differential equations were applied to the study of infectious diseases [8]. In 1926, Kermack and McKendrick [9] established the first SIR (Susceptible-Infected-Recovered) compartment model to study the spread of the Black Death in London and the plague in Mumbai. Subsequently, they established the SIS (Susceptible-Infected-Susceptible) compartment model in 1932 and proposed the famous threshold theory for the spread of the epidemic [10]. Since the pioneering work of Kermack and Mckendrick, dynamic models of infectious diseases with different propagation laws have sprung up (e.g., SIRS model, Tang et al. [11]; SEIR model, Li and Muldowney [12]; SEIRS model, Bjørnstad et al. [13]; MSEIR model, Hethcote [14]). In this work, we focus on studying the dynamics of infectious diseases with SIS compartment structures, such as common cold, influenza and dysentery.

How do infectious diseases spread? What determines the extinction of infectious diseases? There is strong evidence that human factors can significantly influence the transmission dynamics of infectious diseases. Mathematically, there have been numerous studies exploring the mechanisms by which anthropogenic factors influence the dynamics of infectious diseases. See, for instance, immunization, Gao et al. [15], Starnini et al. [16]; isolation, Te Vrugt et al. [17], Bolzoni et al. [18]; media coverage, Cai et al. [19]; time delay, Agaba et al. [20, 21]. It is worth pointing out that in traditional mathematical modeling research on epidemics, medical conditions are usually considered as a fixed constant. In fact, when a large-scale outbreak of infectious diseases occurs, the supply of medical resources may be insufficient, and this scenario is especially prone to occur in economically underdeveloped areas. For instance, in the early stage of the COVID-19 outbreak, the demand for medical supplies such as masks and ventilators could not be met in some countries. Overall, it is of great practical significance to consider the impact of resource constraints on the transmission dynamics of infectious diseases.

In this paper, we develop a mathematical framework based on differential equations to describe SIS infectious disease dynamics. This framework allows us to study how do resource constraints affect disease persistence and extinction through feedback on effective incidence rate. The remaining sections are arranged as follows. In Sect. 2, the disease-resource model is derived. In Sect. 3, a rigorous mathematical analysis is developed to learn the global dynamics of the disease-resource model. Sect. 4 ends the paper with a conclusion.

2 Model description

A general SIS compartment model can be described by the following system of ordinary differential equations

$$\begin{aligned} \begin{aligned} S'&= \Lambda -\beta SI-\mu S+\gamma I,\\ I'&= \beta SI-(\mu +\gamma ) I,\\ \end{aligned} \end{aligned}$$
(1)

where S(t) and I(t) represent the population densities of susceptible and infected individuals at time t, respectively. The parameter \(\Lambda \) denotes the constant input rate of the population, and \(\beta \) represents the effective incidence rate of infected individuals, reflecting the ability of infected individuals to infect susceptible individuals. \(\mu \) is the natural mortality rate, and \(\gamma \) is the removal rate of infected individuals. Since \(S'+I'=\Lambda -\mu (S+I),\) we can verify that the compact set

$$\begin{aligned} C_1=\left\{ (S,I)\in \mathbb {R}_+^2: S+I=\frac{\Lambda }{\mu }\right\} \end{aligned}$$

is positively invariant of Model (1) given \(S(0)+I(0)=\frac{\Lambda }{\mu }\). Therefore, instead of Model (1), we can study the following model

$$\begin{aligned} \begin{aligned} I'=\beta \left( \frac{\Lambda }{\mu }-I\right) I-(\mu +\gamma ) I. \end{aligned} \end{aligned}$$
(2)

A simple calculation shows that Model (2) has the following explicit solution

$$\begin{aligned} \begin{aligned} I(t)=\frac{\frac{1}{\beta }\left( \beta \frac{\Lambda }{\mu }-\mu -\gamma \right) I(0)e^{\left( \beta \frac{\Lambda }{\mu }-\mu -\gamma \right) t}}{\frac{1}{\beta }\left( \beta \frac{\Lambda }{\mu }-\mu -\gamma \right) +I(0)\left[ e^{\left( \beta \frac{\Lambda }{\mu }-\mu -\gamma \right) t}-1\right] }. \end{aligned} \end{aligned}$$

Therefore, the global dynamics of Model (2) can be completely determined by the critical threshold

$$\begin{aligned} \mathcal {R}_0=\frac{\Lambda \beta }{\mu (\mu +\gamma )}. \end{aligned}$$

1. When \(\mathcal {R}_0<1\), Model (2) always has a unique disease-free equilibrium \(I_0=0\), which is globally asymptotically stable.

2. When \(\mathcal {R}_0>1\), the disease-free equilibrium \(I_0\) is unstable, and Model (2) has a unique endemic equilibrium \(I^*=\frac{\mu +\gamma }{\beta }(\mathcal {R}_0-1)\), which is globally asymptotically stable.

The abundance of resources at time t (i.e., R(t)) is determined by the inflow and outflow of resources. We assume that the inflow rate of resources depends on the total population size, with a proportionality coefficient \(\alpha \). The outflow of resources consists of two parts: the basic resource consumption and the disease-caused resource consumption. The basic consumption of resources is mainly attributed to susceptible individuals, and the resource consumption rate of a single susceptible individual is \(m_1R\). The resource consumption due to illness depends on the scale of infected individuals, and the resource consumption rate of a single infected person is \(m_2R\). According to common sense, the infected individuals are more urgently resource-dependent than the susceptible individuals. Therefore, we assume throughout the paper that \(m_2>m_1\). Based on the discussion above, the dynamics of resources can be described by

$$\begin{aligned} \begin{aligned} R'=\alpha \frac{\Lambda }{\mu }-m_1\frac{\Lambda }{\mu }R-(m_2-m_1)IR. \end{aligned} \end{aligned}$$
(3)

Depending on the type of resource, there are several ways to incorporate the effect of resource abundance on disease dynamics. In this work, we consider the scenario where resource abundance (such as masks, etc.) mainly affects the effective incidence rate, and assume that

$$\begin{aligned} \beta (R)=\frac{\beta _0}{1+pR}, \end{aligned}$$

where \(\beta _0\) represents the basic effective incidence rate in the resource-free state, and the parameter \(p>0\) describes the effect of resource abundance on the effective incidence rate. One can also consider scenarios where resource abundance affects other terms. For instance, when the resource represents medical devices such as ventilators, scenarios where resource abundance mainly affects the recovery rate of infected individuals can be considered. Based on the above discussion, we obtain the SIS infectious disease model under dynamic resource constraints as follows

$$\begin{aligned} \begin{aligned} I'=&\frac{\beta _0I}{1+pR}\left( \frac{\Lambda }{\mu }-I\right) -(\mu +\gamma ) I,\\ R'=&\alpha \frac{\Lambda }{\mu }-m_1\frac{\Lambda }{\mu }R-(m_2-m_1)IR. \end{aligned} \end{aligned}$$
(4)

In the following section, we assess the impact of resource constraints on disease transmission by analyzing the global dynamics of Model (4).

3 Equilibrium, critical threshold and global dynamics

We first identify the positive invariant set of Model (4), which reflects the biological plausibility of the model. Subsequently, we theoretically analyze the existence and stability of equilibria of Model (4), and derive the threshold conditions for disease persistence and extinction.

Lemma 1

(Positive invariant set) The deterministic model (4) is positively invariant in \((I(t),R(t))\in \mathbb {R}_+^2:=\{(x,y)\mid x\ge 0,y\ge 0\}\). For any initial value \((I(0),R(0))\in \mathbb {R}_+^2\), the solution will eventually be attracted to the compact set

$$\begin{aligned} C_2=\left\{ (I,R)\in \mathbb {R}_+^2: 0\le I\le \frac{\Lambda }{\mu }-\frac{\mu +\gamma }{\beta _0},0<R\le \frac{\alpha }{m_1}\right\} . \end{aligned}$$

Proof

See Appendix A. \(\square \)

Remark 1

Lemma 1 suggests that the deterministic model (4) is well biologically defined. Note that the variable I(t) represents the population density of infected individuals, it is realistic for I(t) to remain non-negative and have a positive upper bound. Besides, resource abundance has an upper bound and remains positive definite, reflecting the continued supply of suppliers.

3.1 Existence and local stability of equilibria

Note that an equilibrium of Model (4) should satisfy

$$\begin{aligned} \begin{aligned} 0=&\frac{\beta _0I}{1+pR}\left( \frac{\Lambda }{\mu }-I\right) -(\mu +\gamma ) I,\\ 0=&\frac{\alpha \Lambda }{\mu }-\frac{m_1\Lambda }{\mu }R-(m_2-m_1)IR. \end{aligned} \end{aligned}$$
(5)

We can draw the following intuitive results.

  1. (1)

    Model (4) always has a unique disease-free equilibrium

    $$\begin{aligned} E_0=(0,R_0)=\left( 0,\frac{\alpha }{m_1}\right) . \end{aligned}$$

    In this case, \(R_0=\frac{\alpha }{m_1}\) defines the base supply balance of resources in the disease-free state \(I_0=0\).

  2. (2)

    Model (4) can have up to two interior equilibria

    $$\begin{aligned} E_i^*=(I_i^*,R_i^*)=\left( I_i^*,\frac{\alpha \frac{\Lambda }{\mu }}{m_1\frac{\Lambda }{\mu }+(m_2-m_1)I_i^*}\right) ,~i=1.2, \end{aligned}$$

    where \(I_1^*\) and \(I_2^*\) (\(I_1^*\le I_2^*\)) are the intersections of the quadratic equation g(I) and the horizontal line \(\frac{\Lambda }{\mu }(\mu +\gamma )\alpha p\) in the first quadrant, and

    $$\begin{aligned} \begin{aligned} g(I)=&\left[ \frac{m_1\Lambda }{\mu }+(m_2-m_1)I\right] \left( \beta _0\frac{\Lambda }{\mu }-\mu -\gamma -\beta _0I\right) .\\ \end{aligned} \end{aligned}$$
    (6)

    By simple calculation, the solutions \(I_1^*\) and \(I_2^*\) (if exist) can be expressed as

    $$\begin{aligned} \begin{aligned} I_{1,2}^*=&\frac{(m_2-m_1)\left( \frac{\Lambda }{\mu }\beta _0-\mu -\gamma \right) -\beta _0m_1\frac{\Lambda }{\mu }}{2\beta _0(m_2-m_1)}\\&\pm \frac{1}{2(m_2-m_1)\beta _0}\bigg \{\left[ (m_2-m_1)\left( \frac{\Lambda }{\mu }\beta _0-\mu -\gamma \right) -\beta _0m_1\frac{\Lambda }{\mu }\right] ^2\\&-4(m_2-m_1)\beta _0\frac{\Lambda }{\mu }\left[ \alpha p(\mu +\gamma )-m_1(\beta _0\frac{\Lambda }{\mu }-\mu -\gamma )\right] \bigg \}^{\frac{1}{2}}. \end{aligned} \end{aligned}$$
  3. (3)

    Since the symmetry axis of the quadratic function g(I) is given by

    $$\begin{aligned} I_{ep}=\frac{(m_2-m_1)\left( \frac{\Lambda }{\mu }\beta _0-\mu -\gamma \right) -\beta _0m_1\frac{\Lambda }{\mu }}{2\beta _0(m_2-m_1)}, \end{aligned}$$

    it follows that (i) If sign\([I_{ep}]=-1\) (see Fig. a), the quadratic function g(I) achieves the maximum

    $$\begin{aligned} g(0)=m_1\frac{\Lambda }{\mu }\left( \beta _0\frac{\Lambda }{\mu }-\mu -\gamma \right) :=g_0 \end{aligned}$$

    on the compact set \(C_2\). In this case, Model (4) has no interior equilibrium. (ii) If sign\([I_{ep}]=1\) (see Fig. 1b), the quadratic function g(I) takes the maximum

    $$\begin{aligned} g(I_{ep})=g_0+\frac{\left[ (m_2-m_1)\left( \frac{\Lambda }{\mu }\beta _0-\mu -\gamma \right) -\beta _0m_1\frac{\Lambda }{\mu }\right] ^2}{4\beta _0(m_2-m_1)}:=g_{\max }. \end{aligned}$$

Remark 2

The quadratic function g(I) links the resource consumption rate to the density of infected individuals. It reflects fluctuations in the rate of resource demand as the density of infected individuals and the resource consumption rate increase. Intuitively, \(I_{ep}\) can be regarded as the critical number of infected individuals. When the critical value is exceeded, the resource consumption rate is insufficient to increase the resource demand rate. Therefore, \(g_{\max }\) can be regarded as the maximum possible resource demand rate. The horizontal line \(\frac{\Lambda }{\mu }(\mu +\gamma )\alpha p\) is related to the supply rate of resources and the ability of resources to suppress the effective incidence rate of diseases. It can be considered as the alert resource threshold. From a biological point of view, disease outbreaks may occur when the resource demand rate is above the alert resource threshold.

Next, we present sufficient and necessary conditions for the existence and stability of the equilibria of Model (4). To proceed, we define the critical thresholds

$$\begin{aligned} \mathcal {R}_1=\frac{\Lambda \beta _0}{\mu (\mu +\gamma )}\frac{m_1}{\alpha p+m_1}~\text {and}~\mathcal {R}_2=\frac{g_{\max }}{\frac{\Lambda }{\mu }(\mu +\gamma )\alpha p}. \end{aligned}$$

Since \(\mathcal {R}_0=\frac{\Lambda \beta _0}{\mu (\mu +\gamma )}\) represents the expected number of cases arising directly from one case in a population in which all individuals are susceptible. Therefore, \(\mathcal {R}_1\) denotes the number of people infected by a patient during its average illness period with the intervention of medical resources. From a biological point of view, disease outbreaks occur when \(\mathcal {R}_1>1\). The value of \(\mathcal {R}_2\) determines the maximum number of interior equilibria. Note that \(g_{\max }\) represents the maximum possible resource demand rate, and the horizontal line \(\frac{\Lambda }{\mu }(\mu +\gamma )\alpha p\) denotes the alert resource threshold. Therefore, when \(\mathcal {R}_2>1\), there is a possibility of disease outbreaks. Mathematically, since \(\mathcal {R}_1>1\Leftrightarrow \frac{g_{0}}{\frac{\Lambda }{\mu }(\mu +\gamma )\alpha p}\), it follows that the relation \(\mathcal {R}_2>\mathcal {R}_1\) always holds.

Fig. 1
figure 1

Schematic diagram of the existence of equilibrium of Model (4). The biologically meaningful equilibrium occurs at the intersections of the quadratic function g(I) and the horizontal line \(\frac{\Lambda }{\mu }(\mu +\gamma )\alpha p\) in the first quadrant. a When sign\([I_{ep}]=-1\), Model (4) can have no interior equilibrium (on the line \(\rho _0\)), or one interior equilibrium \(E_2^*\) (on the line \(\rho _1\)). b When sign\([I_{ep}]=1\), Model (4) can have no interior equilibrium (on the line \(\rho _0\)), one interior equilibrium \(E_2^*\) (on the line \(\rho _1\)), or two interior equilibria \(E_1^*\) and \(E_2^*\)(on the line \(\rho _2\))

Full size image

Theorem 1

The deterministic model (4) always has a disease-free equilibrium \(E_0\), and can have up to two interior equilibria \(E_i^*,i=1.2,\) depending on the values of \(\mathcal {R}_1\), \(\mathcal {R}_2\), and the sign of \(I_{ep}\). The sufficient and necessary conditions for the existence and local stability of these equilibria are listed in Table .

Table 1 Existence and local stability of equilibria of Model (4)
Full size table

Proof

Define

$$\begin{aligned} \begin{aligned} f_1(I,R)=&\frac{\beta _0I}{1+pR}\left( \frac{\Lambda }{\mu }-I\right) -(\mu +\gamma ) I,\\ f_2(I,R)=&\frac{\alpha \Lambda }{\mu }-\frac{m_1\Lambda }{\mu }R-(m_2-m_1)IR. \end{aligned} \end{aligned}$$
(7)

An equilibrium \(E^\#=(I^\#,R^\#)\) of Model (4) should satisfy \(f_i(I^\#,R^\#)=0, i=1,2\). Simple calculation shows that Model (4) always has a unique disease-free equilibrium \(E_0=(0,\frac{\alpha }{m_1}).\) When \(I^\#\ne 0,\) solving \(f_1(I^\#,R^\#)=0\), we can obtain that

$$\begin{aligned} R^\#=\frac{\beta _0\frac{\Lambda }{\mu }-\mu -\gamma -\beta _0I^\#}{p(\mu +\gamma )}. \end{aligned}$$
(8)

Substituting (8) into \(f_2(I^\#,R^\#)=0\) gives

$$\begin{aligned} \begin{aligned} h(I^\#):=&\alpha \frac{\Lambda }{\mu }-\frac{1}{p(\mu +\gamma )}g(I^\#)=0,\\ \end{aligned} \end{aligned}$$
(9)

where

$$\begin{aligned} \begin{aligned} g(I)=&\left[ \frac{m_1\Lambda }{\mu }+(m_2-m_1)I\right] \left( \beta _0\frac{\Lambda }{\mu }-\mu -\gamma -\beta _0I\right) .\\ \end{aligned} \end{aligned}$$
(10)

Therefore, the number of equilibria depends on the intersections of the quadratic function \(g(I^\#)\) and the horizontal line \(\frac{\Lambda }{\mu }(\mu +\gamma )\alpha p\) in the first quadrant. By direct calculation, we know that the symmetry axis \(I=I_{ep}\) of the quadratic equation g(I) is given by

$$\begin{aligned} I_{ep}=\frac{(m_2-m_1)\left( \frac{\Lambda }{\mu }\beta _0-\mu -\gamma \right) -\beta _0m_1\frac{\Lambda }{\mu }}{2\beta _0(m_2-m_1)}. \end{aligned}$$

Now, we can divide the discussion into the following cases.

1. When the symmetry axis \(I_{ep}\) of the quadratic equation g(I) is less than 0, i.e., sign\([I_{ep}]=-1\), the quadratic equation g(I) takes the maximum

$$\begin{aligned} g(0)=\frac{m_1\Lambda }{\mu }\left( \beta _0\frac{\Lambda }{\mu }-\mu -\gamma \right) . \end{aligned}$$

Therefore, Model (4) can have zero or one interior equilibrium (see Fig. 1a), depending on the ratio of

$$\begin{aligned} \mathcal {R}_1=\frac{m_1\beta _0\frac{\Lambda }{\mu }}{(\mu +\gamma )(\alpha p+m_1)}. \end{aligned}$$

(1) If \(\mathcal {R}_1\le 1\), Model (4) has no interior equilibrium;

(2) If \(\mathcal {R}_1>1\), Model (4) has a unique interior equilibrium \(E_2^*\).

2. When sign\([I_{ep}]=1,\) the quadratic equation \(g(I^\#)\) takes the maximum

$$\begin{aligned} g_{\max }=g(I_{ep})=g(0)+\frac{\left[ (m_2-m_1)\left( \frac{\Lambda }{\mu }\beta _0-\mu -\gamma \right) -\beta _0m_1\frac{\Lambda }{\mu }\right] ^2}{4\beta _0(m_2-m_1)}. \end{aligned}$$

In this case, Model (4) can have up to two interior equilibria (see Fig. 1b), depending on the ratios of

$$\begin{aligned} \mathcal {R}_1=\frac{m_1\beta _0\frac{\Lambda }{\mu }}{(\mu +\gamma )(\alpha p+m_1)}~\text {and}~\mathcal {R}_2=\frac{g_{\max }}{\frac{\Lambda }{\mu }(\mu +\gamma )\alpha p}. \end{aligned}$$
  1. (1)

    If \(\mathcal {R}_1<1\) and \(\mathcal {R}_2>1\), Model (4) has two interior equilibria \(E_1^*\) and \(E_2^*\);

  2. (2)

    If \(\mathcal {R}_1>1\), Model (4) has a unique interior equilibrium;

  3. (3)

    If \(\mathcal {R}_2<1\), Model (4) has no interior equilibrium.

Next, we analyze the stability of the disease-free equilibrium \(E_0=(0,R_0)=(0,\frac{\alpha }{m_1})\). By direct calculation, the Jacobian matrix of Model (4) at the disease-free equilibrium \(E_0\) can be obtained as

$$\begin{aligned} \begin{aligned} J_{E_0}=\left[ \begin{array}{ll} \frac{\beta _0}{1+pR_0}\frac{\Lambda }{\mu }-\mu -\gamma &{}0\\ -(m_2-m_1)R_0&{}-\frac{m_1\Lambda }{\mu }\\ \end{array}\right] . \end{aligned} \end{aligned}$$
(11)

The two eigenroots of Model (4) at \(E_0\) are

$$\begin{aligned} \lambda _1=-\frac{m_1\Lambda }{\mu }<0 \end{aligned}$$

and

$$\begin{aligned} \lambda _2=\frac{\beta _0m_1}{m_1+p\alpha }\frac{\Lambda }{\mu }-\mu -\gamma <0. \end{aligned}$$

Therefore, the disease-free equilibrium \(E_0\) is locally asymptotically stable provided

$$\begin{aligned} \mathcal {R}_1=\frac{\beta _0\frac{\Lambda }{\mu }}{\mu +\gamma }\frac{m_1}{m_1+p\alpha }<1. \end{aligned}$$

In the following, we analyze the stability of the positive equilibria \(E_i^*,i=1,2\). Estimating the Jacobian matrix of Model (4) at \(E_i^*=(I_i^*,R_i^*)\) yields

$$\begin{aligned} \begin{aligned} J_{E_i^*}=&\left[ \begin{array}{ll} \frac{\beta _0}{1+pR_i^*}\frac{\Lambda }{\mu }-\frac{2\beta _0I_i^*}{1+pR_i^*}-\mu -\gamma &{}{-\frac{p\left( \frac{\Lambda }{\mu }-I_i^*\right) \beta _0I_i^*}{(1+pR_i^*)^2}}\\ -(m_2-m_1)R_i^*&{}-\frac{m_1\Lambda }{\mu }-(m_2-m_1)I_i^*\\ \end{array}\right] \\ =&\left[ \begin{array}{ll} -\frac{\beta _0I_i^*}{1+pR_i^*}&{}{-\frac{p\left( \frac{\Lambda }{\mu }-I_i^*\right) \beta _0I_i^*}{(1+pR_i^*)^2}}\\ -(m_2-m_1)R_i^*&{}-\frac{\alpha \Lambda }{\mu R_i^*}\\ \end{array}\right] .\\ \end{aligned} \end{aligned}$$
(12)

The corresponding characteristic equation is given by

$$\begin{aligned} \lambda ^2+\left( \frac{\beta _0I_i^*}{1+pR_i^*}+\frac{\alpha \Lambda }{\mu R_i^*}\right) \lambda +\det (J_{E_i^*})=0, \end{aligned}$$
(13)

where

$$\begin{aligned} \det (J_{E_i^*})=\frac{\beta _0I_i^*}{1+pR_i^*}\frac{\alpha \Lambda }{\mu R_i^*}-{p(m_2-m_1)R_i^*\frac{\left( \frac{\Lambda }{\mu }-I_i^*\right) \beta _0I_i^*}{(1+pR_i^*)^2}}. \end{aligned}$$

Since \(E_i^*=(I_i^*,R_i^*), i=1,2\) are the interior equilibria of Model (4), the implicit function theorem combined with \(f_1(I_i^*,R_i^*)=0\) implies that there is a continuous differentiable function

$$\begin{aligned} R(I)=\frac{\beta _0\frac{\Lambda }{\mu }-\mu -\gamma -\beta _0I}{p(\mu +\gamma )} \end{aligned}$$
(14)

such that \(R(I_i^*)=0\) and

$$\begin{aligned} \frac{dR(I)}{dI}\mid _{I=I_i^*}=-\frac{\frac{\partial f_1(I,R)}{\partial I}}{\frac{\partial f_1(I,R)}{\partial R}}\mid _{I=I_i^*}. \end{aligned}$$

Substituting Eq. (14) into \(f_2(I,R)\), we obtain that

$$\begin{aligned} f_2(I,R(I))=h(I). \end{aligned}$$
(15)

Take the derivative of Eq. (15) with respect to I, we get that

$$\begin{aligned} \left[ \frac{\partial f_2(I,R(I))}{\partial R}\frac{dR(I)}{dI}+\frac{\partial f_2(I,R(I))}{\partial I}\right] \mid _{I=I_i^*}=\frac{dh(I)}{dI}\mid _{I=I_i^*}. \end{aligned}$$
(16)

Therefore we have

$$\begin{aligned} \begin{aligned} \frac{dh(I)}{dI}\mid _{I=I_i^*}\frac{\partial f_1(I,R)}{\partial R}\mid _{I=I_i^*}=&-\frac{\partial f_2(I,R(I))}{\partial R}\frac{\partial f_1(I,R)}{\partial I}\mid _{I=I_i^*}\\&+\frac{\partial f_2(I,R(I))}{\partial I}\mid _{I=I_i^*}\frac{\partial f_1(I,R)}{\partial R}\mid _{I=I_i^*}\\ =&-\det (J_{E_i^*}). \end{aligned} \end{aligned}$$
(17)

It follows that

$$\begin{aligned} \begin{aligned} \det (J_{E_i^*})=&-\frac{dh(I)}{dI}\mid _{I=I_i^*}\frac{\partial f_1(I,R)}{\partial R}\mid _{I=I_i^*}\\ =&{-\frac{\left( \frac{\Lambda }{\mu }-I_i^*\right) \beta _0I_i^*}{(1+pR_i^*)^2(\mu +\gamma )}g'(I_i^*)}.\\ \end{aligned} \end{aligned}$$
(18)

By the characteristic Eq. (13) we know that the characteristic roots satisfy

$$\begin{aligned} \lambda _1(E_i^*)+\lambda _2(E_i^*)=-\left( \frac{\beta _0I_i^*}{1+pR_i^*}+\frac{\alpha \Lambda }{\mu R_i^*}\right) <0 \end{aligned}$$

and

$$\begin{aligned} \lambda _1(E_i^*)\lambda _2(E_i^*)=\det (J_{E_i^*})={-\frac{\left( \frac{\Lambda }{\mu }-I_i^*\right) \beta _0I_i^*}{(1+pR_i^*)^2(\mu +\gamma )}g'(I_i^*).} \end{aligned}$$

Therefore, we have \(\lambda _1(E_1^*)\lambda _2(E_1^*)<0\) and \(\lambda _1(E_2^*)\lambda _2(E_2^*)>0\). Based on the above discussion, we have the following results:

  1. (1)

    When Model (4) has a unique interior equilibrium \(E_2^*=(I_2^*,R_2^*)\), since \(g'(I_2^*)<0\), we know that the interior equilibrium \(E_2^*\) is locally asymptotically stable.

  2. (1)

    When Model (4) has two interior equilibria \(E_i^*=(I_i^*,R_i^*),i=1,2\), since \(g'(I_1^*)>0\) and \(g'(I_2^*)<0\), we know that the interior equilibrium \(E_1^*\) is unstable and the interior equilibrium \(E_2^*\) is locally asymptotically stable.

This completes the proof of Theorem 1. \(\square \)

Remark 3

Theorem 1 suggests that the local stability of disease-free equilibrium \(E_0\) is completely determined by \(\mathcal {R}_1\). In addition, the number of epidemic equilibria is determined by \(\mathcal {R}_1, \mathcal {R}_2\) and sign\([I_ep]\).

3.2 Global dynamics and bistability

To clarify the global dynamics of Model (4), we next study the global stability of the equilibria \(E_0,E_1^*\) and \(E_2^*\).

Theorem 2

The global dynamics of Model (4) can be summarized as:

  1. (1)

    Persistence. If \(\mathcal {R}_1>1\), the unique interior equilibrium \(E_2^*\) of Model (4) is globally asymptotically stable. In this scenario, the disease will persist.

  2. (1)

    Extinction. If either (i) sign\([I_{ep}]=-1,\mathcal {R}_1<1\) or (ii) \(sign[I_{ep}]=1,\mathcal {R}_2<1\) holds, Model (4) has a unique disease-free equilibrium which is globally asymptotically stable. In this scenario, the disease will become extinct.

  3. (1)

    Bistable. If \(\mathcal {R}_1<1<\mathcal {R}_2\) and sign\([I_{ep}]=1\), Model (4) has bistable between the disease-free equilibrium and the interior equilibrium \(E_2^*\), while \(E_1^*\) always unstable. In this scenario, the extinction of the disease depends on the initial population size and resource reserves.

Proof

Since Pioncare-Bendixson property holds for Model (4), we only need to verify the nonexistence of nontrivial periodic orbit and heteroclinic orbit in \(\text {Int} \mathbb R_+^2\). If this is not the case, define the Euclidean ball as \(U\subset \mathbb R^2\), where \(\bar{U}\) and \(\partial U\) are the closure and boundary of the Euclidean ball U. Let \(\mathcal V\) be the basin of attraction of \(E_2^*\) in \(\text {Int} \mathbb R_+^2\), \(\bar{\mathcal V}\) the closure of \(\mathcal V\) in \(\text {Int} \mathbb R_+^2\). Then it follows from Index Theory for 2-dimensional system [22] that there exists a simple closed rectifiable curve \(\varphi \in \text {Lip}(\partial U\rightarrow \bar{\mathcal V})\) in \(\bar{\mathcal V}\), which is invariant with respect to Model (4). Denote

$$\begin{aligned} \Upsilon (\varphi , \overline{\mathcal {V}})=\{\phi \in \text {Lip}({\overline{U}}\rightarrow \overline{\mathcal {V}}): \phi (\partial U)=\varphi (\partial U) \}. \end{aligned}$$

Then \(\Upsilon (\varphi , \overline{\mathcal {V}})\) is nonempty. Let P be a functional on \(\Upsilon (\varphi , \overline{\mathcal {V}})\) defined by

$$\begin{aligned} P\phi =\int _{{\overline{U}}}\mid \frac{\partial \phi }{\partial w_1}\wedge \frac{\partial \phi }{\partial w_2}\mid , \end{aligned}$$

where \((w_1,w_2)\in {\overline{U}}\), \(\wedge \) is Grassman product. Since \(E_{0}\notin \overline{\mathcal {V}}\) and any positive orbit from an initial point in \( \mathbb R_+^2 \) but not in the positive \(R-\)axis will enter \(\text {Int} \mathbb R_+^2\), it follows that there exists a constant \(\epsilon >0\) such that

$$\begin{aligned} \liminf \limits _{t\rightarrow +\infty }I(t)>\epsilon , \ \liminf \limits _{t\rightarrow +\infty }R(t)>\epsilon \end{aligned}$$

if the initial points lie in \(\overline{\mathcal {V}}\). Thus there exists a compact absorbing set \(\Psi \subset \overline{\mathcal {V}}\). For \(\Psi \), it follows from Li and Muldowney (Proposition 2.2 of [23]) that there exists \(\delta >0\) such that \(P\phi \ge \delta \) for all \(\Upsilon (\varphi , \overline{\mathcal {V}})\) such that \(\phi ({\overline{U}})\subset \Psi \). Let \(x=(I,R)\) and f(x) denote the vector field of Model (4), and let \(\phi _t=x(t,\phi )\). Then \(y_i(t)=\frac{\partial \phi _t}{\partial w_i},i=1,2,\) are solutions of the linear variational equation of Model (4)

$$\begin{aligned} \dot{y}(t)=Df(x(t,\phi ))y(t),\end{aligned}$$
(19)

where \(Df(x(t,\phi ))=J(x(t,\phi ))\) and

$$\begin{aligned} \begin{aligned} J(x(t,\phi ))=&\left( \begin{array}{ll} \frac{\beta _0}{1+pR}\frac{\Lambda }{\mu }-\frac{2\beta _0I}{1+pR}-\mu -\gamma &{}{-\frac{p\left( \frac{\Lambda }{\mu }-I\right) \beta _0I}{(1+pR)^2}}\\ -(m_2-m_1)R&{}-\frac{m_1\Lambda }{\mu }-(m_2-m_1)I\\ \end{array}\right) ,\\ \end{aligned} \end{aligned}$$

and \(z(t)=\frac{\partial \phi _t}{\partial w_1}\wedge \frac{\partial \phi _t}{\partial w_2}\) is a solution of the second compound equation of (19) (see [24, 25]),

$$\begin{aligned} \dot{z}(t)=Df^{[2]}(x(t,\phi ))z(t),\end{aligned}$$
(20)

where

$$\begin{aligned} Df^{[2]}(x(t,\phi ))= \frac{\beta _0}{1+pR}\frac{\Lambda }{\mu }-\frac{2\beta _0I}{1+pR}-\mu -\gamma -\frac{m_1\Lambda }{\mu }-(m_2-m_1)I. \end{aligned}$$
(21)

Rewriting Model (4), we find that

$$\begin{aligned} \frac{I'}{I}=\frac{\beta _0}{1+pR}\left( \frac{\Lambda }{\mu }-I\right) -(\mu +\gamma ).\end{aligned}$$

It then follows that

$$\begin{aligned} Df^{[2]}(x(t,\phi ))\le \frac{\dot{I}}{I}-\frac{m_1\Lambda }{\mu }. \end{aligned}$$

A solution (I(t), R(t)) to Model (4) with initial points in the absorbing set \(\Psi \) exists for all \(t>0\). Thus there exists \(T>0\) such that \(t>T\) implies that

$$\begin{aligned} \int _0^t Df^{[2]}(x(s,\phi ))ds\le \log \frac{I(t)}{I(0)}-\frac{m_1\Lambda }{\mu } t<-\frac{m_1\Lambda }{2\mu }t \end{aligned}$$

for all initial points which is in \(\Psi \). It then follows that

$$\begin{aligned} \begin{aligned} p\phi _t=&\int _{\overline{U}}\mid \frac{\partial \phi _t}{\partial w_1}\wedge \frac{\partial \phi _t}{\partial w_2}\mid \\ \le&\int _{\overline{U}}\mid \frac{\partial \phi }{\partial w_1}\wedge \frac{\partial \phi }{\partial w_2}\mid \exp \left( \int _0^tDf^{[2]}(x(s,\phi ))ds)\right) \\ \le&p\phi \exp \left( -\frac{m_1\Lambda }{2\mu }t\right) . \end{aligned} \end{aligned}$$

Therefore, \(P\phi _t \rightarrow 0\) as \(t \rightarrow \infty \). This contradicts the fact that \(P\phi \ge \delta \) for all \(\Upsilon (\varphi , \overline{\mathcal {V}})\) such that \(\phi ({\overline{U}})\subset \Psi \) since \(\varphi \) is invariant with respect to Model (4), and \(\phi _t(\overline{U})\subset \Psi \) for all sufficiently large t. This contradiction implies that no simple closed rectifiable curve in \(\overline{\mathcal {V}}\) is invariant with respect to Model (4). In particular, it rules out not only nontrivial periodic oribits but also homoclinic and heteroclinic loops since each case gives rise to a simple closed rectifiable curve in \(\overline{\mathcal {V}}\). This completes the proof of Theorem 2. \(\square \)

Remark 4

Theorem 2 shows that there are no nontrivial periodic orbit or heteroclinic orbit in Model (4). Therefore, the global dynamics of Model (4) is completely determined by \(\mathcal {R}_1, \mathcal {R}_2\) and sign\([I_ep]\): (i) If sign\([I_ep]=-1\), then Model (4) undergoes a forward bifurcation as \(\mathcal {R}_1\) passes through 1 from the left. During this process, the disease-free equilibrium \(E_0\) changes from stable to unstable, and a stable endemic equilibrium \(E_2\) appears (see Fig. a). (ii) If sign\([I_ep]=1\), then Model (4) undergoes a backward bifurcation as \(\mathcal {R}_1\) passes through 1 from the right, where Model (4) can have bistability. Moreover, Model (4) undergoes a saddle-node bifurcation at \(R_2^{-1}\) (see Fig. 2b).

Fig. 2
figure 2

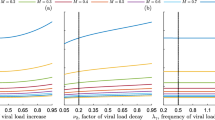
One-parameter bifurcation of Model (4) with \(\Lambda =20, \mu =0.2, \gamma =1.5, \beta _0=0.16, \alpha =1.1, m_1=0.1\), \(p\in (0,3)\), and: (1) a \(m_2=0.11\); (2) b \(m_2=1.1\), where the blue and green lines represent sink and saddle, respectively. (Color available online)

Full size image

4 Conclusion

We provide a mathematical model to describe disease transmission dynamics under resource constraints. The effect of resource constraints is described by the reduction in effective incidence rate, which is expressed as a nonlinear function \(\frac{\beta _0}{1+pR}\), where p represents the inhibitory strength of the unit resource on the effective incidence of the disease. We first verify the positive invariant set of the model, and then present the necessary and sufficient conditions for the existence and local stability of the equilibria. Finally, by excluding the nontrivial periodic orbit and heteroclinic orbit, we obtain the global stability of the equilibria. Specifically, the global dynamics of the deterministic model (4) can be summarized as follows

  1. (1)

    Under the intervention of medical resources, if a patient is able to infect more than one person during the average illness, i.e., \(\mathcal {R}_1>1\), the disease will persist.

  2. (1)

    If the critical number of infected individuals is large enough (i.e., sign\([I_{ep}]=1\)), the maximum possible resource demand rate is greater than the effective supply rate of the resource (i.e.,\(\mathcal {R}_2>1\)) and \(\mathcal {R}_1<1\), then the disease is either persistent at high the level or extinct, depending on the initial level of the infected individuals and the resource abundance.

  3. (1)

    If either sign\([I_{ep}]=-1,\mathcal {R}_1<1\) or sign\([I_{ep}]=1,\mathcal {R}_2<1\) holds, the disease will become extinct.

Along with the above insights, the theoretical framework has some limitations. It is well known that the spatial distribution of diseases can be non-uniform. Therefore incorporating spatial heterogeneity into the proposed framework would be an interesting topic. Furthermore, environmental stochasticity has been widely incorporated into various biological systems (e.g., epidemic and population systems [19, 26, 27]). While we provide a full picture of the dynamics of the SIS infectious disease model under resource constraints, we do not incorporate possible consequences of environmental stochasticity. Evaluating how environmental stochasticity, in conjunction with resource constraints, affects SIS infectious disease dynamics will be future work.