1 Introduction

Carbonate reservoirs are the important sources of hydrocarbons, accounting for half of world’s oil and gas reserves (Li and Chen 2013; Yousef et al. 2014). The Tahe Oilfield is the largest oilfield found in the Paleozoic marine carbonates in China (Li et al. 2014a). The successful exploitation of this oilfield can significantly reduce the crisis of the hydrocarbon shortage in China.

The Tahe Oilfield is located in the middle of the South Tarim Uplift in the Tarim Basin, China, with an area of 2400 km2 (Li et al. 2014b). The Ordovician reservoir in the Tahe Oilfield is an example of fractured-vuggy carbonate reservoirs (Li 2013). The reservoir space is complicated because of the co-existence of vugs, fractures, and large caves in these reservoirs (Xu et al. 2012). Large caves serve as the main storage space, while fractures act as the primary flow paths with only a little oil accumulated in them (Lv et al. 2011; Zhang and Wang 2004). On the other hand, the carbonate matrix exhibits ultra-low permeability and almost no storage ability. Therefore, a fractured-vuggy unit is considered as the basic production unit during the exploitation of these carbonate reservoirs (Yi et al. 2011; Rong et al. 2013). This type of reservoir is characterized by serious heterogeneity, random distribution, and complex co-location of fractures and vugs, and various filling types and filling percentages of storage space. Therefore, fractured-vuggy carbonate reservoirs are very complex with multiple oil–water systems and the existence of bottom water, which makes hydrocarbon production difficult (Popov et al. 2009; Lucia et al. 2003).

And so far, in most of the numerical simulations of fractured-vuggy carbonate reservoirs, this type of reservoir is taken as equivalent to sandstone reservoirs, e.g., CMG, Eclipse (Presho et al. 2011; Wu et al. 2011; Guo et al. 2012). A commercial numerical simulator specialized for fractured-vuggy carbonate reservoirs has not yet been developed. Consequently, fundamental experimental research is required to provide a theoretical foundation for numerical simulations.

Previous research has been conducted on fractured-vuggy reservoirs through physical simulations (Cruz et al. 2001; Zheng et al. 2010; Zhang et al. 2011; Jia et al. 2013; Xu et al. 2013). Cruz et al. (2001) performed water-displacing oil experiments using a two-dimensional vuggy fractured porous cell, took photographs of the water front, measured the flow area corresponding to oil and water, and finally developed a theoretical model based on the experimental results. Zheng et al. (2010) designed and constructed a cylindrical core model, according to actual conditions of a fractured-vuggy carbonate reservoir. Water-displacing oil experiments were conducted and it is found that oil recovery, water cut, and water breakthrough were significantly impacted by fractured-vuggy structures. Zhang et al. (2011) built a single-phase fluid flow pattern in fractured-vuggy media with different vug densities, and concluded that with an increase in vug density, the pressure gradient at the same velocity declined and the critical velocity increased. However, due to the limitations of dimensionality, similarity design, and other factors, three-dimensional fluid flow in porous media is difficult to simulate reliably in these models. In this paper, a three-dimensional physical model is designed and built based on a geological example unit in the Tahe Oilfield and similarity criteria. Bottom water drive is conducted to validate the 3D physical model according to well history and then the optimization of water injection modes is performed by means of continuous, intermittent, and pulsed injection of water.

The experimental results may provide an insight into the later production with water injection and numerical simulations of fractured-vuggy carbonate reservoirs.

2 Geological example and well history

2.1 Example reservoir

Five wells, S48, T401, TK411, TK426CH, and TK467, in the S48 unit in the Tahe Oilfield were chosen as examples to design a 3D physical model, as shown in Fig. 1. The red part in Fig. 1 indicates the area of influence of the chosen well groups. The longitudinal sections of the reservoir are presented in Fig. 2.

Fig. 1
figure 1

Geological conditions of the example reservoir

Full size image
Fig. 2
figure 2

Longitudinal sections of the reservoir

Full size image

2.2 Well history

A 3D physical model was constructed based on the example of the geology of the S48 unit. Bottom water drive was employed in the S48 unit in the early stage of production. The physical model was required to be similar to actual reservoir conditions so that experimental results are as reliable as possible. Hence, it is imperative to understand and analyze the practical production situations during bottom water drive. Tables 1 and 2 depict well history information of the S48 unit. According to well history and other information reported earlier (Zhu et al. 2009; Hu et al. 2013), an oil recovery of 20 %–23 % was obtained at the end of bottom water drive in this unit.

Table 1 Production histories of 5 wells with bottom water drive in the S48 unit
Full size table
Table 2 Annual data of the S48 unit with bottom water drive
Full size table

3 Physical model design and fabrication

3.1 Similarity design

According to previous studies of physical simulation (Elkaddifi et al. 2008; Zhang et al. 2008; Bünger and Herwig 2009; Zuta and Fjelde 2011; Wang et al. 2014), some similarity criteria, such as geometric similarity, kinematic similarity, dynamic similarity, and characteristic parameter similarity, were adopted to insure the similarity between the physical model and the geological example.

However, it was impossible to achieve similarity of all parameters. Thus, a dimensional analysis method was introduced to simplify the similarity criterions.

The characteristics of oil and water two-phase flow in a multi-well fractured-vuggy unit should be taken into account and relevant physical parameters were considered as illustrated in Table 3.

Table 3 Physical parameters and dimensions related to oil and water two-phase flow in a multi-well fractured-vuggy unit
Full size table

According to Buckingham’s pi-theorem (Haftkhani and Arabi 2013), ρ, u, and l were chosen as basic parameters, and the physical parameters with the same dimensions were classified as a group. The similarity criterion group is obtained as shown in Table 4.

Table 4 Similarity criterion group of the multi-well fractured-vuggy unit
Full size table

For a specific flow model, the flow field in the physical model is generally similar to that in the actual reservoir when some main similarity criteria are achieved (Kang and Tang. 2014; Nam et al. 2014). The ratio of the cave diameter to the diameter of the area of influence was chosen as a criterion for geometric similarity. Since the bottom water drive is required to be simulated, the liquid production rate and production duration should be similar to actual situations, so π6 and π7 in Table 4 were chosen as kinematic similarity criteria. The Reynolds number should be considered when dynamic similarity is discussed. Meanwhile, the ratio of pressure to gravity that influences the fluid distribution in displacement processes needed to be considered. In addition, the physical model should comply with the similarity theorem on some characteristic parameters, such as pseudo coordination number and filling percentage. Since it is difficult for a physical model to satisfy multiple similarity criteria simultaneously, the Reynolds number should always be given priority.

The index of the similarity criteria was calculated according to similarity coefficients. A similarity coefficient is the ratio of field parameters to model parameters. If a certain index of the similarity criterion is 1, this model parameter is fully compliant with the field parameter. Based on the discussion mentioned above, the similarity coefficients and similarity indices of the physical model are obtained as shown in Tables 5 and 6.

Table 5 Comparison of parameters of the example reservoir and the physical model
Full size table
Table 6 Similarity indices of the physical model
Full size table

3.2 Model fabrication

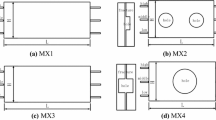
Longitudinal sections of the example reservoir were divided into six layers, as shown in Fig. 3. Caves and fractures were carved in each core based on the example reservoir. After that, these six cores were bonded together in a given order. The flow paths of the bottom water and well locations were designed, and a three-dimensional model was fabricated. Finally, the model was put into a cylindrical mold and it was encapsulated and fixated with epoxy resin, as presented in Fig. 4. More details of the physical model were described elsewhere (Hou et al. 2014).

Fig. 3
figure 3

Comparison of the fractured-vuggy structures between the physical model and the real core for each layer

Full size image
Fig. 4
figure 4

The real core after combination

Full size image

3.3 Fracture and cave structures and well locations

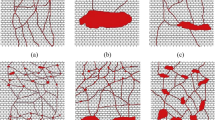
A fractured-vuggy unit with a complex structure was formed in a 3D space, as shown in Fig. 5. In order to make the model similar to the actual formation, caves and fractures were filled with gravel in a certain order of completely filled, half-filled, and unfilled from bottom to top.

Fig. 5
figure 5

Fractured-vuggy structure inside the three-dimensional physical model

Full size image

Five wells were drilled in the model according to the designed depths and locations. These wells were drilled in different reservoir bodies, i.e., cave and fracture. Wells were divided into two types: one is cave-well which is marked by “D” and the other is fracture-well marked by “L.” Figure 6 illustrates the well locations and Table 7 shows the well parameters.

Fig. 6
figure 6

Well locations in the three-dimensional physical model

Full size image
Table 7 Well parameters of the models
Full size table

4 Experimental

4.1 Experimental apparatus and materials

The experimental apparatus (Fig. 7) included a 3D physical model, three intermediate containers, two water injection pumps with a pressure range of 0–30 MPa and a flow rate range of 0.01–10.00 mL/min, several pressure transducers, some six-port valves, etc.

Fig. 7
figure 7

Schematic diagram of experimental setups for the bottom water drive (a) and the water injection mode optimization (b)

Full size image

The simulated oil used was a mixture of kerosene and dehydrated crude, with a viscosity of 65 mPa s at 25 °C. The simulated formation water used had a salinity of 2 × 105 mg/L.

4.2 Experimental procedures

The experimental procedures are as follows:

  1. (1)

    The physical model was evacuated and then saturated with the simulated formation water at 10 mL/min from pipelines 6 in Fig. 7. The total volume of water injected into the model was measured to calculate the pore volume (PV) of fractures and caves in the physical model.

  2. (2)

    The model was flooded with the simulated oil at 10 mL/min from pipelines 13 from the top of the model and the water was drained from pipelines 6. This was continued until no more water was drained. The total volume of water displaced from the model was measured, and the initial oil saturation and the water saturation of the model were then calculated.

  3. (3)

    As shown in Fig. 7a, the simulated formation water was continuously introduced into the bottom of the model; the water injection rate was varied to simulate the stage of depletion of a bottom water drive reservoir. The initial water injection rate was set at 10 mL/min and then decreased to 6 mL/min after 15 min, and to 4 mL/min after another 5 min. The injection rate was kept at 4 mL/min until a 98 % water cut was reached in one of these five production wells. The oil and water production rate was monitored to calculate oil recovery and periodic water cut. Five wells were put into production in the order D1, D2, L2, L3, and L1, as depicted in Table 8.

    Table 8 Well startup order in the bottom water drive model
    Full size table
  4. (4)

    During the bottom water drive, the water cut of Well L1 reached 98 % first. This well was then switched to be an injection well. After the bottom water drive, the experimental apparatus was set up as shown in Fig. 7b. Water was subsequently introduced into the model through Well L1; water injection rates at different waterflood projects are listed in Table 9. Each production well was shut in once its water cut reached 98 %. The experiment was stopped when the four production wells were all shut in. The oil and water production rates were monitored to calculate the oil recovery and periodic water cut.

    Table 9 Experimental schemes for optimizing water injection
    Full size table

5 Experimental results and discussion

5.1 Performance of the bottom water drive model

The production performance of the bottom water drive model constructed in this study is shown in Fig. 8. The oil recoveries of five production wells increased slowly at this stage, i.e., the oil production rate declined, and the water cut of fluids produced from Well L1 increased as the bottom water energy was depleted.

Fig. 8
figure 8

Production performance of the bottom water drive at the depletion stage

Full size image

Water breakthrough occurred immediately in Well L1 and its water cut rose rapidly after this well was put into production. This is because Well L1 was the deepest well (Table 7). Experimental results are consistent with actual production situation. The experiment was stopped when the water cut of fluids produced from Well L1 reached 98 %. The total oil recovery was about 22.1 %, which is in agreement with the actual oil recovery in the S48 unit. Thus, experimental results verified that the 3D physical model had similarity to the example reservoir (S48 unit).

5.2 Optimization of water injection schemes

Due to the viscosity difference between water and oil in the water/oil interface, the flow rate of water is higher than that of oil under the same differential pressure. When the differential pressure is high enough, water can probably flow vertically upward. Therefore, a conical water/oil interface was formed, which is known as bottom water coning (Xiao et al. 2010).

By injecting water into the reservoir through a drowned well to supply energy, bottom water coning could be mitigated and the intrusive water phase could be suppressed toward the opposite direction (Lu et al. 2009). However, different water injection modes exert different effects on mitigating water coning. Therefore, the objective of the following work is to optimize water injection modes, including continuous injection (constant rate), intermittent injection, and pulsed injection of water.

5.2.1 Overall effect of subsequent water injection

Figures 9 and 10 show the dynamic curves of oil recovery and differential pressure for three water injection schemes, respectively.

Fig. 9
figure 9

Dynamic oil recovery curve

Full size image
Fig. 10
figure 10

Injection pressure during water injection

Full size image

No matter which water injection scheme was performed, the oil recovery increased substantially at the beginning and then continued to rise smoothly until the oil recovery became relatively stable as no more oil was being produced. The highest oil recovery of 47.0 % was obtained after pulsed injection of water. Similar oil recoveries, 44.7 % and 44.3 %, respectively, were obtained after continuous and intermittent injection of water.

The differential pressure fluctuated significantly during intermittent and pulsed injection of water (Fig. 10). The amplitude of pressure fluctuations was relatively large when water was intermittently injected into Well L1 every 25 min, while the frequency of pressure fluctuations was relatively high during pulsed injection of water. This indicates that unsteady-state water injection, including intermittent injection and pulsed injection, might promote the instability of fluid flow rate, flow direction, and pressure distribution in the model. In this way, the water displacement efficiency was improved. However, the displacement efficiency of intermittent injection was not as good as expected. This is due to the serious heterogeneity and the complex structure of fractures and caves in the fractured-vuggy reservoir model.

5.2.2 Production performance at the subsequent water injection stage

Figures 11, 12, 13, and 14 present the oil recovery and water cut of four production wells at the subsequent water injection stage, respectively.

Fig. 11
figure 11

Dynamic curves of oil recovery and water cut of Well L2

Full size image
Fig. 12
figure 12

Dynamic curves of oil recovery and water cut of Well D1

Full size image
Fig. 13
figure 13

Dynamic curves of oil recovery and water cut of Well D2

Full size image
Fig. 14
figure 14

Dynamic curves of oil recovery and water cut of Well L3

Full size image

Well L2 was the nearest to the injection well L1, and its well depth was similar to Well L1. Therefore, water breakthrough occurred immediately in Well L2 when the water was injected into Well L1. Correspondingly, the water cut of Well L2 increased to 100 % rapidly. The incremental oil recovery was only about 0.1 %–0.2 %.

Because Well D1 was drilled deeply into a cave that was near to injection well L1, water breakthrough occurred easily during subsequent water injection. The final oil recovery of Well D1 after intermittent injection was the highest among these three water injection modes. During intermittent injection, the injection pressure of Well D1 was high enough to suppress bottom water coning. Therefore, the oil/water co-production duration of Well D1 was long and its oil recovery was relative high. However, the incremental oil recovery was still at a low level, less than 5.5 %. All these phenomena can be attributed to the well location, well depth, and the early water breakthrough.

Well D2 was comparatively far from Well L1 and the gravity effect in this well was relatively strong due to a bottom cave. The injection pressure was very low and only supplied bottom water energy during continuous water injection. So, the oil recovery of this well was not high after continuous water injection. On the other hand, the advantage of intermittent and pulsed injection of water was apparent. By changing the injection rate, pressure fluctuations were generated. The formation pressure distribution was changed and the oil–water flow was promoted between fractures and caves. In this way, the sweep efficiency and the displacement efficiency were improved.

Well L3 was also comparatively far away from injection well L1. Unlike Well D2, Well L3 was a fracture-well, and the well depth was the shallowest among those five wells. Therefore, the production performance of Well L3 was completely different from others. During intermittent injection, the injection pressure increased rapidly and water breakthrough occurred easily. However, after the water injection ended, water and oil were hard to redistribute due to the high viscosity resistance and slight gravity effect in fractures. This also led to a relative low oil recovery in Well L3 after immediate injection of water. During pulsed water injection, the high injection rate led to a high pressure increase and caused an early water breakthrough; however, the frequently fluctuated pressure induced a long duration of oil and water co-production, and led to a high final oil recovery.

Due to the complicated fractured-vuggy structure, well location, and well depth, not all the wells exhibited effective response to these three water injection modes. As a whole, the rate of increase of water cut during intermittent and pulsed injection of water was higher than that during continuous water injection. Unsteady-state injection of water indeed enhances water displacement efficiency to some extent compared with steady-state water injection.

6 Conclusions

  1. (1)

    Based on a multi-well fractured-vuggy geological example unit in the Tahe Oilfield, a large-scale three-dimensional physical model was designed and constructed to simulate the fluid flow according to similarity criteria. Several factors were considered in the design, including storage types, filling types, and filling percentages of storage space.

  2. (2)

    The depletion production was conducted by changing the bottom water injection rate. Oil recovery of the physical model was similar to that of the field cases, which verified the reliability of the physical model.

  3. (3)

    During pulsed injection of water, unbalanced formation pressure was caused, and the swept volume was expanded, and consequently the highest oil recovery increment was achieved. Intermittent injection presented the same effect as pulsed injection. However, similar to continuous injection, intermittent injection was influenced by factors including fractured-vuggy connected manner, well depth, and injection–production relationship. Continuous injection and intermittent injection finally get a comparatively low oil recovery.

  4. (4)

    If a well is deep and close to the injection well, water breakthrough may occur earlier and water cut rises more rapidly. Besides, production performances of the fracture-well and the cave-well are completely different due to the difference in gravity effect and viscosity resistance.