Experimental study and a proposed new approach for thermodynamic modeling of wax precipitation in crude oil using a PC-SAFT model

Abstract

A powerful method is necessary for thermodynamic modeling of wax phase behavior in crude oils, such as the perturbed-chain statistical associating fluid theory (PC-SAFT). In this work, a new approach based on the wax appearance temperature of crude oil was proposed to estimate PC-SAFT parameters in thermodynamic modeling of wax precipitation from crude oil. The proposed approach was verified using experimental data obtained in this work and also with those reported in the literature. In order to compare the performance of the PC-SAFT model with previous models, the wax precipitation experimental data were correlated using previous models such as the solid solution model and multi-solid phase model. The results showed that the PC-SAFT model can correlate more accurately the wax precipitation experimental data of crude oil than the previous models, with an absolute average deviation less than 0.4 %. Also, a series of dynamic experiments were carried out to determine the rheological behavior of waxy crude oil in the absence and presence of a flow improver such as ethylene–vinyl acetate copolymer. It was found that the apparent viscosity of waxy crude oil decreased with increasing shear rate. Also, the results showed that the performance of flow improver was dependent on its molecular weight.

1 Introduction

Crude oil is a complex mixture of hydrocarbons, consisting of waxes, asphaltenes, resins, aromatics, and naphthenics. Wax precipitation has a substantial effect on oil production and transportation. Wax precipitation can result many problems, such as decreased production rates of crude oil, increased power requirements, and failure of facilities. Wax is the high molecular weight paraffin fraction of crude oil and can be separated by reduction in oil temperature below the pour point of crude oil. The solubility of high molecular weight waxes in crude oil decreases with decreasing temperature. In the transportation of waxy crude oil in a cold environment at temperatures below the oil pour point, the temperature gradient of the oil creates a concentration gradient of the dissolved waxes due to their difference in solubility. The driving force, created by the concentration gradient, transfers the waxes from the oil toward the pipe wall where they precipitate and form a solid phase. The solid phase reduces the available area for oil flow, and in turn causes a drop in the pipe flow capacity. In order to predict the wax precipitation conditions, a reliable thermodynamic model is necessary. Several thermodynamic models for estimation of wax precipitation have been reported in the literature (Barker and Henderson 1969; Chen et al. 2009). A literature review (Dalirsefat and Feyzi 2007) indicates that the models for wax precipitation have been developed by two different approaches. The first important approach for modeling of wax precipitation uses a cubic equation of state (EOS) for vapor–liquid equilibrium and an activity coefficient model for solid–liquid equilibrium. These models are based on solid solution (SS) theory which assumes that all the components in the solid phase are miscible in all proportions (Won 1968, 1989; Hansen et al. 1988; Pedersen et al. 1991; Zuo et al. 2001; Ji et al. 2004). Chen et al. (2009) proposed new correlations for the melting points and solid–solid transition temperatures of treated paraffin based on the experimental results from differential scanning calorimetry (DSC). They first estimated the required thermodynamic properties of pure n-paraffin and then a new approach based on the UNIQUAC equation was described. Finally, the impact of pressure on wax phase equilibrium was studied. The second approach based on a multi-solid (MS) phase model uses only an EOS for all phases in equilibrium. In fact, an EOS is used directly for vapor–liquid equilibrium, and solid phase is described indirectly from the EOS by fugacity ratio. The multi-solid (MS) phase model assumes that each pure or pseudo-component precipitate constitutes a separate solid phase which is not miscible with other solid phases (Lira-Galeana et al. 1996; Pan and Firoozabadi 1997; Nichita et al. 2001; Escobar-Remolina 2006; Dalirsefat and Feyzi 2007). The thermodynamic models are developed based on complex properties, such as interaction coefficient, critical properties, acentric factor, solubility parameter, and molecular weight. They are not specified for long chain waxes in crude oil. In order to develop a thermodynamic model for modeling wax phase behavior in crude oils, a powerful method is necessary. The perturbed-chain statistical associating fluid theoretical (PC-SAFT) equation of state is especially useful for modeling phase behavior of complex structure, such as wax in crude oil. Recently, the asphaltene precipitation in Iranian crude oils was investigated by using the PC-SAFT equation of state (Sedghi and Goual 2014; Punnapala and Vargas 2013; María 2014; Panuganti et al. 2012; Leekumjorn and Krejbjerg 2013; Jafari Behbahani et al. 2011a, b, c, 2012, 2013a, b, c, 2014a, b, c, 2015). The effect of wax inhibitors on pour point and rheological properties of Iranian waxy crude oils were investigated (Jafari Ansaroudi et al. 2013; Jafari Behbahani 2008, 2014a, b). In this work, a PC-SAFT model has been proposed to predict the wax appearance temperature and the amount of precipitated wax. A new approach for estimation of PC-SAFT parameters of wax precipitation in crude oil has been proposed in this work. In order to compare the performance of the PC-SAFT model, the wax precipitation experimental data obtained in this work and reported in the literature were correlated using previous models such as solid solution and multi-solid phase models. Also, the pour points and viscosity of the studied crude oil were measured at different concentrations of flow improvers.

2 Materials and methods

2.1 Material

A waxy crude oil was used for investigation of rheological behavior in the absence/presence of flow improver such as ethylene–vinyl acetate copolymer. The physical characteristic of crude oil is shown in Tables 1 and 2.

Table 1 The characterization of studied waxy crude oil

Table 2 The composition and molecular weight of the studied crude oil

Two types of polymers with different properties were selected as flow improver (denoted as EVA#1 and EVA#2). The characteristics of the flow improvers are provided in Table 3.

Table 3 Characteristics of used polymers

2.2 Experimental apparatus

Apparent viscosity as a function of temperature was measured with a Haake RV12 concentric cylinder viscometer equipped with double gap geometry. Molecular weights of polymers were determined by Waters gel permeation chromatography (GPC) in a Shimadzu LC10AD system equipped with a refractive index detector and ultrastyragel columns of 106, 105, 104, and 500 A connected in series. Tetrahydrofuran was used as the mobile phase, at a flow rate of 1 mL/min. Composition of the polymer was measured by an elemental analyzer (PerkinElmer 2400). This elemental analyzer is a proven instrument for rapid determination of the carbon, hydrogen, nitrogen, sulfur, or oxygen content in organic and other types of materials. It has the capability of handling a wide variety of sample types in the fields of pharmaceuticals, polymers, chemicals, environment, and energy, including solids, liquids, volatile, and viscous samples.

Based on the classical Pregl-Dumas method, samples are combusted in a pure oxygen environment, with the resultant combustion gases measured in an automated fashion. Wax and asphaltene contents were determined according to BP-327, IP-143, respectively. Pour points were measured by ASTM D-97 method.

2.3 Experimental procedure

An appropriate quantity of flow improvers were dissolved in cyclohexane (improver to cyclohexane molar ratio of 1:2), and added to crude oil and then heated in a thermostatic bath maintained at 50 °C. The viscosity and shear stress of the studied crude oil was measured at different shear rates in the range of 10–100 s⁻¹. The rheological data cover the temperature range of 0–27 °C. Also, the pour points and viscosity of the studied crude oil were measured at different concentrations of flow improvers.

3 Theoretical section

The existing thermodynamic models (solid solution (SS) theory and multi-solid (MS) phase model) are based on complex properties, such as interaction coefficient, critical properties, acentric factor, solubility parameter, and molecular weight which are not specified for long chain waxes. A reliable model is necessary to predict the wax precipitation condition in crude oil. In this work, in order to model wax precipitation, the PC-SAFT EOS was used for prediction of the wax appearance temperature and the mass of precipitated wax. Also, a new approach for investigating the PC-SAFT EOS parameters of wax in the crude oil was proposed in this work. In order to examine the performance of the PC-SAFT model, the wax precipitation experimental data reported in the literature were correlated using the above-mentioned models such as the Ji model (Ji et al. 2004) from the solid solution (SS) category and the Lira-Galeana model (Lira-Galeana et al. 1996) from the multi-solid (MS) phase category.

3.1 PC-SAFT model

To calculate the equilibrium between oil and wax phases, it is obviously necessary to use an accurate thermodynamic model. The PC-SAFT equation of state properly predicts the phase behavior of mixtures containing long chain fluids similar to the large wax molecules. The thermodynamic phase behavior of fluid mixtures can be described by perturbation theory. In this approach, the properties of a fluid are obtained by expanding about the same properties of a reference fluid. The statistical associating fluid theory (SAFT) equation of state was developed by Chapman et al. (1989) by applying and extending Wertheim’s first-order perturbation theory (Wertheim 1984, 1986) to chain molecules, and Gonzalez et al. (2007) used the PC-SAFT EOS for asphaltene phase behavior modeling. In this theory, molecules are modeled as chains of bonded spherical segments and the properties of a fluid are obtained by expanding about the same properties of a reference fluid. Gross and Sadowski (2001) proposed the perturbed-chain modification (PC-SAFT) to account for the effects of chain length on the segment dispersion energy, by extending the perturbation theory of Barker and Henderson (1969) to a hard chain reference (Koyuncu et al. 2002). This version of SAFT properly predicts the phase behavior of mixtures containing high molecular weight fluids such as the large wax molecules.

The PC-SAFT model describes the residual Helmholtz free energy (A ^res) of a mixture of nonassociating fluid as follows:

$$\frac{{A^{\text{res}} }}{\text{RT}} = \frac{{A^{\text{seg}} }}{\text{RT}} + \frac{{A^{\text{chain}} }}{\text{RT}} = m \times \left( {\frac{{A_{0}^{\text{hs}} }}{\text{RT}} + \frac{{A_{0}^{\text{disp}} }}{\text{RT}}} \right) + \frac{{A^{\text{chain}} }}{\text{RT}},$$

(1)

where A ^seg is segment contribution to the mixture Helmholtz free energy, A ^chain is the chain contribution to the mixture Helmholtz free Energy, A ^hs₀ is the hard-sphere contribution to the mixture Helmholtz free energy, and A ^disp₀ is the dispersion contribution to the mixture Helmholtz free energy.

The PC-SAFT equations are described in Appendix 1.

3.1.1 Proposed approach for estimation of the PC-SAFT parameters in modeling of wax precipitation

When describing a component using an equation of state, values of critical temperature, critical pressure, and acentric factor are required. However, it is almost impossible to measure directly critical properties for longer-chain wax due to thermal decomposition at high temperatures. As a result, different correlations have been suggested in the literature for estimation of critical properties and acentric factors for these components. However, estimated values using these correlations can differ considerably, potentially having a negative effect on the reliability of wax precipitation prediction. In this work, a new approach based on the wax appearance temperature of crude oil was proposed to estimate PC-SAFT parameters in thermodynamic modeling of wax precipitation from crude oil as follows:

• (1) Three pseudo-components describe the liquid phase: wax, aromatics/resins, and asphaltenes. The characterization of this phase is conducted based on the liquid fluid compositional information and SARA (waxes, aromatics/resins, and asphaltene) analysis.

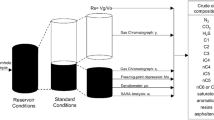
• (2) The wax PC-SAFT EOS parameters in the crude oil are tuned to meet the wax appearance temperature of the crude oil. In order to characterize wax cut, as shown in Fig. 1, saturates were divided into two sections: one precipitated and another not precipitated, and the perturbed-chain form of the statistical associating fluid theory (PC-SAFT) parameters were tuned to match the wax appearance temperature of crude oil.

  Fig. 1

  

  The proposed characterization of wax cut in crude oil (A is asphaltenes and R is resins)

• (3) The PC-SAFT EOS parameters for asphaltene are fitted to precipitation onset measurements based on ambient titrations and/or depressurization measurements.

• (4) The PC-SAFT parameters for aromatics/resins pseudo-components are calculated from their average molecular weight. The aromatics/resins pseudo-component is linearly weighted by the aromaticity parameter between poly-nuclear-aromatic (PNA) and benzene-derivative components, characterized by following equations:

  $$m = 0.0139{\text{MW}} + 1.2988$$

  (2)
  $$\frac{\varepsilon }{k} = 119.4\ln ({\text{MW}}) - 230.21$$

  (3)
  $$\sigma = (0.0597{\text{MW}} + 4.2015) \times 10^{ - 10} /m.$$

  (4)

• (5) The wax phase behavior modeling procedure for an oil starts with the definition of four pseudo-components that represent the gas phase: nitrogen (N₂), carbon dioxide (CO₂), methane (CH₄), and light pseudo-components (hydrocarbons C₂ and heavier). The average molecular weight of the light pseudo-component is used to estimate the PC-SAFT EOS parameters. Gross and Sadowski (2001) identified the three pure component parameters required for nonassociating molecules of n-alkanes by correlating their vapor pressures and liquid volumes.

  $$m = 0.0253{\text{MW}} + 0.9263$$

  (5)
  $$\sigma = (0.1037{\text{MW}} + 2.7985) \times 10^{ - 10} /m$$

  (6)
  $$\frac{\varepsilon }{k} = 32.8\ln ({\text{MW}}) + 80.398,$$

  (7)

  where MW is the molecular weight, m is the average of pure species segment number, σ is the segment diameter, and ε is the depth of the pair potential.

One advantage of the SAFT-based equations of state is their ability to predict chain length of pure component parameters. In this model, the parameters for the pseudo-components in oil can be determined on the basis of their average molar mass correlations for aromatic and n-alkane fractions.

3.2 Multi-solid phase model

In multi-solid (MS) wax models developed by Lira-Galeana et al. (1996), each solid phase is considered as a pure component which does not mix with other solid phases and can exist as a pure solid (solid assumption). The number and the identity of precipitating components are obtained from Michelsen’s phase stability analysis (Michelsen 1982) which states that component i may exist as a pure solid:

$$f_{i} (P,T,z)\, - \,f_{{{\text{pure}},i}}^{s} (P,T)\, \ge \,0.0\quad i\, = \,1,2, \ldots ,n,$$

(8)

where f _i (P,T, z) is the fugacity of component i with feed composition z and SSS is the fugacity of pure component i in solid phase. This model is based on the precipitation of certain heavy components of crude with average properties and performs calculations for the liquid/multi-solid phase. The criterion of vapor–liquid–solid equilibrium is that the fugacities for every component i, must satisfy the following equations:

$$f_{i}^{V} = f_{i}^{L} = f_{{{\text{pure}},i}}^{s} (P,T)\quad i = 1,2, \ldots ,n$$

(9)

$$f_{i}^{V} = f_{i}^{L} \quad i = 1,2, \ldots ,n,$$

(10)

where f is the fugacity, N is the total number of components, and $f_{{{\text{pure}},i}}^{s}$ is the fugacity of the pure solid phase. The fugacities of each component in the vapor and liquid phases are calculated by the equation of state. This model is described in Appendix 2.

3.3 Solid solution (SS) theory

These models are based on solid solution (SS) theory which assumes that all the components in the solid phase are miscible in all proportions. In solid solution theory, the solid phase is a solid solution, stable or not, of all the components that crystallize. To solve the equilibrium problems, an equation of state (EOS) plus activity coefficient are used. Produced reservoir hydrocarbon fluids under pipeline conditions commonly consist of liquid and vapor phases. This model uses a cubic EOS for vapor–liquid equilibrium and an activity coefficient model for solid–liquid equilibrium. In the solid solution model, the selection of suitable activity coefficient models for description of solid and liquid phase behavior is the main part of the modeling. This model is described in Appendix 3.

3.4 Model validation

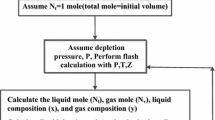
To verify the performance of the proposed model for calculating wax precipitation from crude oil, numerical simulation runs were conducted for experiments performed in this work and given in the literature (Pauly et al. 2004; Pedersen et al. 1991; Chen et al. 2009). In this work, solutions (Tables 6, 10) (Chen et al. 2009) and mixtures 1–5 (Fig. 5) (Pauly et al. 2004) were used to verify the performance of the proposed model for calculating wax precipitation from crude oil. Wax precipitation experimental data in crude oil were correlated by adjusting the parameters of the PC-SAFT model to achieve the best match with the experimental data using MATLAB software. For optimization and determination of the model parameters [i.e., the segment diameter (σ), depth of pair potential (ε/k), and the average of the pure species segment number (m)], history matching was used. In this study, the square root of the sum of differences between measured and calculated wax appearance temperature data was defined as the objective function:

$${\text{Objective}}\,\,{\text{Function}} = \sqrt {\sum\nolimits_{i = 1}^{n} {\left( {(T)_{\text{measured}} - (T)_{\text{calculated}} } \right)}^{2} }.$$

(11)

As a result, the model parameters obtained by optimization are σ, ε/k, and m. A genetic optimization algorithm was used in combination with the numerical scheme to obtain parameters of the PC-SAFT model (σ, ε/k, and m) by fitting the experimental data. The performance of the proposed model for correlating the wax precipitation of the experimental data reported in the literature was compared to those obtained using the Ji model (Ji et al. 2004) from solid solution (SS) category and Lira-Galeana model (Lira-Galeana et al. 1996) from multi-solid (MS) phase category. The absolute deviation of the correlated WAT values obtained for the studied models from their experimental values was calculated by the following relation:

$$AD (\% ) = \frac{{\left| {T_{\text{EXP}} - T_{\text{Cal}} } \right|}}{{T_{\text{EXP}} }} \times 100.$$

(12)

The amount of the precipitated wax for one mole of oil feed is calculated as follows:

$$\begin{aligned}&{\text{Precipitated}}\,{\text{wax}}\,{\text{weight}}\,\% \\ &\quad = \frac{{{\text{Weight}}\,{\text{of}}\,{\text{precipitated}}\,{\text{wax}}}}{{{\text{Weight}}\,{\text{of}}\,{\text{oil}}\,{\text{feed}}}} \times 100.\end{aligned}$$

(13)

Also, the aromaticity parameter (γ) determines the aromatics/resins trend to behave as PNA or benzene derivatives. To quantify the degree of aromaticity, γ will take a value between one, for PNA, and zero, for benzene derivatives. The aromaticity parameter is tuned for the fluid to meet the experimental values of stock-tank-oil (STO) density, STO refractive index, and bubble point for crude oil (Jafari Behbahani et al. 2011a, 2012, 2013a). The aromaticity value for this crude oil was determined to be 0.98 which indicates a close behavior to PNA components.

4 Results and discussion

The main objective of this section is to investigate the performance of the PC-SAFT model for calculating WAT and the weight percent of wax precipitation using a proposed approach to estimation the PC-SAFT parameters based on the wax appearance temperature of crude oil. Also, the performance of the PC-SAFT model for calculating WAT and the weight percent of wax precipitation has been compared with those obtained using the Ji model from the solid solution (SS) category and the Lira-Galeana model from the multi-solid (MS) phase category for the experimental data given in this work and given in the literature. A series of experiments was carried out to investigate the rheological behavior of crude oil using the waxy crude oil sample in the absence/presence of flow improver such as ethylene–vinyl acetate copolymer. The rheological data of the studied crude oil are shown in Fig. 2 at temperature range of 0–27 °C and shear rate range of 10–100 s⁻¹.

Fig. 2

The rheological behavior of the studied crude oil at different temperatures and shear rates, a at −1 °C, b 5 °C, c 10 °C, d 15 °C

Figure 2 shows that with increasing shear rate, the apparent viscosity decreases dramatically. Results show that the shear rate has a considerable effect on viscosity particularly at temperatures below the pour point. At high temperatures above the pour point, the waxy crude oil behaves like a typical homogeneous isotropic liquid with Newtonian characteristics. At temperatures below the pour point, the amount of dissolved wax starts to reach its saturation limit, forming a solid solution in the crude, which leads to a sharp increase of viscosity. Under these circumstances, the viscosity is influenced by two parameters: the effect of temperature reduction that causes viscosity increase against the shear rate that tends to lower it. Further cooling causes formation of a gel network, leading to a progressive rise in viscosity at relatively small dynamic gel strength. On the other hand, the energy exerted by shearing and dissipated in the crude leads to disruption of these bonds and accumulated deformation of the crude gel structure occurs.

Figure 3 shows the influence of the flow improver on the pour points. Results demonstrate a significant reduction in the pour point of the studied crude oil for different concentrations of flow improver, in particular for EVA#1.

Fig. 3

The pour point behavior of the studied crude oil at different concentrations of flow improvers

It can be found that the higher molecular weight flow improver displays better efficiency on pour point of the studied crude oil. The experimental data for the amount and composition of wax precipitated from treated and untreated oil at different temperatures are shown in Tables 4, 5.

Table 4 The weight percent of wax precipitated from pure crude oil and crude oil treated with EVA#1

Table 5 The weight percent of wax precipitated from crude oil treated with EVA#2

Table 6 shows the values of correlation parameters in the PC-SAFT model for crude oil used in this work and for crude oil taken from the literature (Pedersen et al. 1991) (oil 10, 12, 15). It should be noted that the parameters of saturates, aromatics, and asphaltenes were calculated from crude oil in this work and other parameters taken from the literature (Pedersen et al. 1991) (oil 10, 12, 15).

Table 6 The values of approach parameters for PC-SAFT model

The data points which are used in the tuning procedure were taken from the literature (Pedersen et al. 1991) (oil 10, 12, 15) and the data points which are predicted by the PC-SAFT model and new approach in this work were taken from the literature (Pauly et al. 2004) (oil 1–5).

Figure 4 shows the performance of the PC-SAFT model and other thermodynamic models in correlating the wax precipitation weight percent in crude oil used in this work.

Fig. 4

Comparison of the performance of the PC-SAFT model with other thermodynamic models in correlating the wax precipitation weight percent in crude oil used in this work at 0 °C (a) and 12 °C (b)

Tables 7, 8, and 9 show the average absolute deviations (AADs) of wax precipitation from the experimental data of crude oil in this work and given in the literature (Pauly et al. 2004) using the PC-SAFT model and other thermodynamic models.

Table 7 Deviation (%) of the correlated wax precipitation weight percent from the experimental results by the PC-SAFT model and the studied thermodynamic models (for crude oil used in this work)

Table 8 Deviation (%) of the correlated wax precipitation weight percent from the experimental results by the PC-SAFT model and the studied thermodynamic models (for crude oil treated with EVA#1)

Table 9 Deviation (%) of the correlated wax precipitation weight percent from experimental results by the PC-SAFT model and the studied thermodynamic models (crude oil treated with EVA#2)

Figure 5 shows the deviation of the predicted wax precipitation weight percent from their experimental results by using studied models.

Fig. 5

Deviation of the correlated wax precipitation weight percent from the experimental results of crude oil in this work by the studied thermodynamic models—a solution 1, b solution 2, c mixture 5

It should be noted that the solution 1, solution 2, and mixture 5 are waxy solutions.

Also, Table 10 shows the values of parameters for the MS model.

Table 10 The values of parameters for MS model

The results show that PC-SAFT model can predict more accurately than the Ji model from the solid solution (SS) category and the Lira-Galeana model from the multi-solid (MS) phase category, with deviation between 2.3 % and 5.5 %.

Wax molecules contain highly nonspherical and associating molecules. Also, waxes containing long chains are mixtures with large-size asymmetry. In such cases, a more appropriate model is the one that incorporates both the chain length (molecular shape) and molecular association. The PC-SAFT model provides a method for describing the thermodynamics of the complex molecules such as wax, because the PC-SAFT model is based on statistical mechanics and can accurately predict the phase behavior of long chain of wax in crude oil.

The chain term in SAFT is successful in reproducing the equilibrium properties of wax with long chains. Also, the obtained results confirm that the Lira-Galeana model from the multi-solid (MS) phase category is capable of correlating the wax precipitation experimental data with the AADs of 11.5 %–16.8 %, whereas the Ji model from the solid solution (SS) category predicts the wax precipitation experimental data with the AADs of 19.2 %–25.3 %. It should be noted that the Ji model based on solid solution (SS) theory used two types of thermodynamic models to describe the nonideality of liquid phase, which makes this model thermodynamically inconsistent. It is observed from the curves that the Lira-Galeana model and Ji model overestimate the amount of precipitated wax. It should be noted that the amount of flow improvers in wax solution is so little that its contribution to the molar composition of the original paraffin solution can be neglected. In other words, the molar composition of solution with and without flow improvers is the same. The effect of flow improvers on the thermodynamic behavior of waxy oil is modeled as a reduction in the WAT and wax precipitation. In this case, the approaches which are used to describe wax precipitation in waxy oil are suitable for the wax-flow improvers system. Also, it can be observed from sensitivity analysis that the model is also sensitive to the techniques for estimation of critical properties (T _c, P _c) and acentric factor pseudo-components.

5 Conclusions

In this work, the PC-SAFT model was used to estimate precipitated wax weight percent in crude oil and the model was verified using the experimental data obtained in this work and also given in the literature. The performance of the PC-SAFT model in prediction of precipitated wax weight percent was compared with those obtained using the Ji model based on solid solution (SS) theory and Lira-Galeana model from the multi-solid (MS) phase category as follows:

• (1) In this work, a new approach based on the wax appearance temperature of crude oil has been proposed to estimate the PC-SAFT parameters in thermodynamic modeling of wax precipitation from crude oil.

• (2) It can be concluded that the PC-SAFT model can predict more accurately the experimental data when compared with the Ji model from the solid solution (SS) category and the Lira-Galeana model from the multi-solid (MS) phase category with a deviation of between 2.3 % and 5.5 %. One advantage of the SAFT-based equations of state is their ability to predict the chain length dependence of the pure component parameters. In this model, the parameters for the pseudo-components in the oil can be determined on the basis of their average molar mass correlations for aromatic and n-alkane.

• (3) The obtained results indicate that the Lira-Galeana model from the multi-solid (MS) phase category can predict more accurately the experimental data than the Ji model from the solid solution (SS) category.

• (4) It is obvious that by increasing the shear rate, the apparent viscosity decreases dramatically. Results show that the shear rate has a considerable effect on decreasing viscosity particularly at temperatures below the pour point.

• (5) Results demonstrate a significant reduction in the pour point of the studied crude oil for different concentrations of flow improver, in particular for EVA#1. It was found that the higher molecular weight flow improver displays a greater effect on the pour point of the studied crude oil.

• (6) It is obvious that increasing the shear rate decreases the apparent viscosity dramatically. Results show that the shear rate has a considerable effect on decreasing viscosity particularly at temperatures below the pour point.

Appendices

Appendix 1

The average segment number of the mixture, m, is an average of the pure species’ segment number, m_i, weighted by the species’ compositions:

$$m = \sum\nolimits_{i} {x_{i} \cdot m_{i} }.$$

(14)

The Mansoori–Carnahan–Starling–Leland (1971) equation of state provides the free energy contribution of the hard-sphere mixtures:

$$\frac{{A_{0}^{{{\text{hs}}}} }}{{{\text{RT}}}} = 6\left[ {\frac{{(\xi _{2}^{3} + 3\xi _{1} \xi _{2} \xi _{3} - 3\xi _{1} \xi _{2} \xi _{3}^{2} )}}{{\xi _{3} (1 - \xi _{3} )^{2} }} - (\xi _{0} - \xi _{2}^{3} /\xi _{3}^{2} )ln(1 - \xi _{3} )} \right]/\pi \rho$$

(15)

$$\xi_{k} = \left( {\frac{\pi \rho }{6}} \right)\sum\nolimits_{i} {x_{i} \cdot m_{i} \cdot d_{ii}^{k} }$$

(16)

$$d_{ii} = \sigma_{i} \left\{ {1 - 0.12\exp \left( {\frac{\varepsilon }{k}} \right)} \right\}.$$

(17)

The contribution to A ^res due to chain formation is given by

$$\frac{{A^{{{\text{chain}}}} }}{{{\text{RT}}}} = \sum\nolimits_{i} {x_{i} (1 - m_{i} )\ln g_{{{\text{hs}}}} (d_{{ii}} )},$$

(18)

where g _hs(d _ii) is the hard-sphere pair correlation function at contact given by

$$g_{hs} (d_{ii} ) = \frac{1}{{1 - \xi_{3} }} + 3d_{ii} /2\left( {\frac{{\xi_{2} }}{{1 - \xi_{3}^{2} }}} \right) + 2\left( {\frac{{d_{ii} }}{2}} \right)^{2} \left( {\xi_{2}^{2} /(1 - \xi_{3} )^3} \right).$$

(19)

The PC-SAFT model incorporates the effects of chain length on the segment dispersion energy. The perturbed-chain dispersion contribution is given by

$$\frac{{A_{0}^{{{\text{disp}}}} }}{{{\text{RT}}}} = \frac{{A_{1} }}{{{\text{RT}}}} + \frac{{A_{2} }}{{{\text{RT}}}}$$

(20)

$$\frac{{A_{1} }}{\text{RT}} = - 2\pi \rho I_{1} (\eta ,m)\sum\nolimits_{i} {\sum\nolimits_{j} {x_{i} \cdot x_{j} \cdot } } m_{i} \cdot m_{j} \cdot \sigma_{ij}^{3} \left( {\frac{{\varepsilon_{ij} }}{kT}} \right)$$

(21)

$$\frac{{A_{2} }}{\text{RT}} = - \pi \rho I_{2} (\eta ,m) \cdot 1/\sum\nolimits_{i} {\sum\nolimits_{j} {x_{i} \cdot x_{j} \cdot } } m_{i} \cdot m_{j} \cdot \sigma_{ij}^{3} \left( {\frac{{\varepsilon_{ij} }}{kT}} \right)$$

(22)

$$\sigma_{ij} = 0.5(\sigma_{i} + \sigma_{j} )$$

(23)

$$\varepsilon_{ij} = (1 - k_{ij} )\sqrt {\varepsilon_{ij} } \varepsilon_{jj}.$$

(24)

I ₁ and I ₂ are functions of the system packing fraction and average segment number.

Appendix 2

The solid phase fugacities of the pure components, f ^s_pure,i , can be calculated from the fugacity ratio expressed as follows:

$$\ln \left( {\frac{{f^{s} }}{{f^{L} }}} \right){\text{Pure}},i = \frac{{\Delta h_{i}^{t} }}{RT}\left( {\frac{T}{{T_{i}^{f} }} - 1} \right)\frac{{\Delta C_{Pi} }}{R}\left[ {1 - \frac{T}{{T_{i}^{f} }} + \ln \left( {\frac{{T_{i}^{f} }}{T}} \right)} \right],$$

(25)

where T ^f _i is the fusion (melting) temperature.

$$\Delta C_{Pi} = C_{pi}^{L} - C_{pi}^{s},$$

(26)

where C ^L _pi and C ^S _pi are the heat capacity of pure component i at constant pressure corresponding to liquid and solid phases, respectively.

$$\Delta h_{i}^{t} = \Delta h_{i}^{f} - \Delta h_{i}^{tr},$$

(27)

where ∆h ^f _i and ∆h ^tr _i are the enthalpy of fusion and the enthalpy of first solid-state transition, respectively. By using the above equation and an EOS, fugacity in solid and liquid phases, and the numbers of the precipitated solid phases can be calculated. Solid–liquid equilibrium calculations have been performed by using equilibrium and material balance equations. The fugacity coefficient of component i is calculated by an EOS model. Among the EOS models available, the modified PR equation of state is used.

$$P = \frac{\text{RT}}{V - b} - \frac{a}{V(V + b) + b(V - b)}.$$

(28)

The parameters a and b of a pure component are described by the conventional critical parameters approach. The critical properties and acentric factor required in the evaluation of equation of state parameters are obtained from the Gasem’s correlations (Ghanaei et al. 2007). For mixtures, the conventional linear mixing rule is kept for the parameter b:

$$b = \sum\nolimits_{i} {x_{i} b_{i} },$$

(29)

whereas for the parameter a, the LCV mixing rule is used.

$$\frac{a}{{b{\text{RT}}}} = \left( {\frac{\lambda }{{A_{v} }} + \frac{1 - \lambda }{{A_{m} }}} \right)\left( {\frac{{G^{E} }}{\text{RT}}} \right) + \frac{1 - \lambda }{{A_{m} }}\sum\nolimits_{i} {\ln \left( {\frac{b}{{b_{i} }}} \right)} + \sum\nolimits_{i} {x_{i} \frac{{a_{i} }}{{b_{i} {\text{RT}}}}},$$

(30)

where A _m , A _v are constant, then the fugacity coefficient of component i in a mixture, for the PR EOS, is given by the following equation:

$$\ln \varphi_{i}^{L} = \frac{{b_{i} }}{b}\left( {\frac{\text{PV}}{\text{RT}} - 1} \right) - \ln \frac{P(V - b)}{\text{RT}} - \frac{{\alpha_{i} }}{2\sqrt 2 }\ln \left[ {\frac{V + (1 + \sqrt 2 )b}{V + (1 - \sqrt 2 )b}} \right]$$

(31)

$$\alpha_{i} = \left( {\frac{\lambda }{{A_{v} }} + \frac{1 - \lambda }{{A_{m} }}} \right)\ln \gamma_{i} + \frac{1 - \lambda }{{A_{m} }}\ln \left( {\left( {\frac{b}{{b_{i} }}} \right) + \frac{b}{{b_{i} }} - 1} \right) + \frac{{a_{i} }}{{b_{i} {\text{RT}}}}.$$

(32)

Appendix 3

The criterion of vapor–liquid–solid equilibrium is that the fugacities for every component i must satisfy the following equations:

$$f_{i}^{V} = f_{i}^{L} = f_{{{\text{pure}},i}}^{s} (P,T)\quad i = 1,2, \ldots ,n$$

(33)

$$f_{i}^{V} = f_{i}^{L} \quad i = 1,2, \ldots ,n,$$

(34)

where f is the fugacity, n is the total number of components, and N _s is the number of solid phases determined. The fugacity of each component in the vapor and liquid phases is calculated by the equation of state. The fugacity coefficient of component i in the liquid phase is calculated by an EOS/G ^E model. The modified PR equation of state is used. The activity coefficient of component i is calculated using the UNIFAC method. It is assumed that for mixtures containing alkanes only, the residual term in the UNIFAC model is zero. Thus, mixtures containing different alkanes are described by the combinatorial term. The Staverman–Guggenheim combinatorial term, which is used in UNIFAC, is (Gao et al. 2001)

$$\ln \gamma_{i} = \ln \frac{{\phi_{i} }}{{x_{i} }} + 1 - \frac{{\phi_{i} }}{{x_{i} }} - \frac{Z}{2}q_{I} \left( {\ln \left( {\frac{{\phi_{i} }}{{\theta_{i} }}} \right) + 1 - \frac{{\phi_{i} }}{{\theta_{i} }}} \right),$$

(35)

where Z is the coordination number. In this work, ri and qi have been obtained from the following relations by data fitting presented in the literature (Ji et al. 2004):

$$r_{i} = 0.6744C_{ni} + 0.4534$$

(36)

$$q_{i} = 0.54C_{ni} + 0.616.$$

(37)