Introduction

Assumption of parallelism in geological modelling

Knowledge about angular relationships between geological interfaces plays a significant role in subsurface geological modelling. The assumption of geologic interfaces parallelism is used in many modelling environments and related geological software (Lajaunie et al. 1997; Calcagno et al. 2008; Caumon et al. 2013; de la Varga et al. 2018; Grose et al. 2021). For example, (Calcagno et al. 2008) assume in the GeoModeller software (http://www.geomodeller.com) that all geological interfaces belong to a series of sub-parallel surfaces. However, terms such as “sub-conformable” (Carmichael and Ailleres 2016; Carena et al. 2019), “sub-parallel” (Wellmann and Regenauer-Lieb 2012) or “layer-cake” (Thiele et al. 2016) are qualitative and do not have the capacity of answering the question, to which extent two geologic interfaces are parallel?

We acknowledge that the modelling assumption of parallelism may be of great practical utility (Caumon et al. 2013; Grose et al. 2021) allowing geological models comprising conformable interfaces to be constructed using a reasonable geometric constraint. Although several interpolation constraints can be applied to alleviate the rigidity of the parallelism assumption, the limitation of using them is that they can sometimes be subjective which affects uncertainty of the resulting geological model (Grose et al. 2021). Moreover, the number of genetically related strata comprising a conformable succession may not always be known in advance. A next problem is that an angular unconformity with a low angle of discordance may appear conformable at a local scale (Groshong 2006) and in such a case this assumption may be a source of the cognitive bias (see Liang et al. 2021 for exaplanation). In geological mapping, distinguishing conformable contacts from low-angle unconformities is difficult but extremely important to the correct map interpretation (Groshong 2006).

Angular unconformities

Deviations from the assumed parallelism between contacts of layers may be attributed to angular unconformities. For example, angular unconformities develop where tectonically tilted older strata have been eroded and have subsequently been overlain by younger strata (Shanmugam 1988). Thus, knowledge about angular unconformities is important for determining the timing of tectonic activity (Shanmugam 1988).

The criteria to detect angular unconformity usually employ the relational approach, i.e. discordance of dip (Shanmugam 1988) between geologic layers. If seismic data is processed, the seismic expression of angular unconformities is assumed to be a function of the difference in dip of the strata separated by the unconformity surface (Shanmugam 1988). There are also methods of detecting angular unconformities which do not employ the relational approach. For example, (Carena and Friedrich 2018) infer the existence of unconformities by observing dips of individual layers and comparing them with the assumed original depositional angles. If the dip angles are considered exceptionally high, the corresponding layer may indicate the existence of an unconformity.

Study introduction

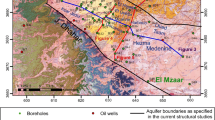
We propose a workflow to investigate spatial distribution of angular distance between geologic interfaces. This workflow is relational in that it requires \(n\) input surfaces to generate all possible pairs for angular distance measurements. It allows the detection of geometric anomalies—observations that deviate from the assumed parallelism between contacts. The proposed method is demonstrated within Kraków-Silesian Homocline (KSH), a natural slope of a country-scale synclinorium with preferred dip direction of layers and accompanying geologic contacts to NE (Fig. 1B). We discuss the results by comparing the resulting distributions within sub-conformable and unconformable horizons. From a methodological perspective, our method can be conceptualised as generalization of slope maps for which the angular distance is measured between a considered interface and a horizontal surface.

Fig. 1
figure 1

A Simplified geological map of Poland without Cenozoic formations (after Osika et al. 1972; Karnkowski 2008) modified) and the location of area studied. CZ—Częstochowa, FSH—Fore-Sudetic Homocline, HCS—Holy Cross Mountains, KA—Kujavian Anticlinorium, KSH—Kraków-Silesian Homocline, MS—Miechów Synclinorium, PA—Pomeranian Anticlinorium, SM—Sudety Mountains. B Geological map of the studied part of the Kraków-Silesian Homocline (after (Dadlez et al. 2000), simplified) and the location of boreholes studied. C Lithostratigraphy and chronostratigraphy of the Middle and Upper Jurassic deposits from the Kraków-Silesian region (after Kopik 1998; Matyja and Wierzbowski 2000, 2006a, b; Matyja and Głowniak 2003; Barski et al. 2004; Pieńkowski 2004; Matyja et al. 2006; Wierzbowski 2017) with an idealized lithological log from the Częstochowa-Kłobuck area

Full size image

Geological setting

Regional setting

The study area located in the northern part of the KSH (Fig. 1A, B) was selected because it was well recognized by drilling for its proven Fe ore deposits whose exploitation is now abandoned.

The KSH, together with Fore-Sudetic Homocline (FSH) (Fig. 1A), occupies the south-east edge of thick sedimentary cover of Permian to Mesozoic age (Stupnicka and Stempień-Sałek 2016; Narkiewicz 2020) formed over older microplates added to the western margin of the East European Craton and assembled into Pangea during Variscan phases (Pharaoh et al. 2006) on the territory of present-day Poland. Thus, the older rocks, which underlie the KSH, were folded and faulted ultimately during Carboniferous-to-Permian tectonic episodes. Elevations of that times were subsequently flattened out and the plain was covered consecutively by Permian, Triassic, Jurassic and Cretaceous deposits, predominantly clastic and carbonate series with common hiatuses, lying unconformably on the Paleozoic or Precambrian basement (Buła et al. 2015). This formation was folded during Late Cretaceous-early Paleocene inversion (Dadlez et al. 1995; Słonka and Krzywiec 2019). As a result, layered plate forming both the FSH and KSH was tilted and inclined towards the northeast, and can be treated as south-western slope of adjacent Szczecin-Łódź-Miechów Synclinorium (Fig. 1A).

Since the early Alpine orogenic movements the KSH has been existing as northern foreland of the Western Carpathians (WC) (Fig. 1A) which resulted from oblique northward push of ALCAPA microplate (Márton et al. 1999). This oblique convergence accompanied by large-scale counter clockwise strike–slip deformation was experienced by the KSH in several ways.

First, southern part of the homocline, being overthrusted by the WC and partially incorporated into the vast tectonic depression of the Carpathian Foredeep (Fig. 1A), has started subsiding in a step-like manner (Krokowski 1984) and layers in this part of the KSH locally dip to the S.

Second, a new fault system appeared in the transpressional and transtensional stress field and older faults of various generations were reactivated when their position favored faulting in this field. Examples of the former include a number of latitudinal horsts and grabens resulted from large scale northwards overthrusts of the WC orogenic units (Krokowski 1984). In turn, the rejuvenated dislocations formed sets of tensile, oblique-slip and strike-slip faults that constituted migration paths for hydrothermal solutions that have contributed to giant accumulation of Zn-Pb ores in the KSH (Teper 2007). The timing of metals emplacement that has been determined for the period between 138.5 and 200 Ma (Jacher-Śliwczyńska 2008; Sutkowska 2009) indicates the approximate age of those faults reactivation.

In situ measured stresses (Jarosiński 2005) and fault displacement (Briestenský et al. 2021) together with determined focal mechanisms of recent seismic events (Teper 1998; Mendecki et al. 2020) support the claim that the convergence accompanied by rotation of the ALCAPA persists to this day, which results episodically in movements on the faults in the WC foreland (Teper and Sagan 1995; Lewandowski 2007). Since the WC foreland consists of the Carpathian Foredeep, the KSH and the Upper Silesian Coal Basin, the oblique northward shift of the ALCAPA microplate also affects the neotectonics of the KSH. Neotectonic movements could cause, among others, local and sporadic exceptions from the general NE dip of the KSH due to fault-related bending of strata (Krokowski 1984; Bednarek et al. 1992; Matyszkiewicz and Krajewski 1996) accompanying mainly latitudinal dislocations in the southern part of the homocline.

Stratigraphy

The interval of strata studied in this paper includes Middle and Upper Jurassic rocks, covered with distinct angular unconformity by Quaternary sediments (Fig. 1C). The Middle Jurassic succession starts with sandy deposits referred to as the Kościeliska Beds, consisting of sands, sandstones and heteroliths. Their age was determined as Early Bajocian and possibly the earliest Late Bajocian (Kopik 1998). They commonly lie on the Lower Jurassic (Toarcian) deposits with a stratigraphic hiatus, although it is possible that in some locations the succession is complete and it may comprise also Aalenian deposits (Kopik 1998). The position of the upper boundary of the Kościeliska Beds is disputable. Formally, it is situated within sandy interval, on the hiatus horizon separating Lower and Upper Bajocian (Kopik 1998). However, in practice, this horizon is often hard to identify and the boundary is conventionally put on the top of sandstone complex. In this paper, the latter approach is applied.

The Kościeliska Beds are overlain by thick mudstone complex referred to as the Częstochowa Ore-Bearing Clay Formation. It consists of dark-grey, organic-rich mudstones with several horizons of siderite and calcareous concretions. The age of these deposits was determined as Late Bajocian—Late Bathonian (Kopik 1998; Matyja and Wierzbowski 2000, 2006a, b; Barski et al. 2004).

Upwards, the Częstochowa Ore-Bearing Clay Formation passes into condensed siliciclastic and carbonate deposits, including limestones, marlstones and sandstones, with a nodular limestone bed and stromatolite layer at the top (Kopik 1979). Their age was determined as Callovian (Kopik 1998; Matyja et al. 2006). For a long time, the lower boundary of Callovian succession was considered to be erosional (Kopik 1998). However, some new stratigraphic data have shown that the Bathonian-Callovian transition could be, at least in places, continuous (Barski et al. 2004). The upper boundary of Callovian lies within extremely condensed interval and in some locations is accompanied by stratigraphic hiatus (Kopik 1997; Matyja et al. 2006).

Callovian is overlain by carbonate deposits referred to as the Częstochowa Sponge Limestone Formation, consisting of bedded and massive sponge-cyanobacteria limestones of Early Oxfordian to Early Kimmeridgian age (Matyja and Głowniak 2003; Matyja and Wierzbowski 2006a; Wierzbowski 2017). In the upper part, deposits of the Częstochowa Sponge Limestone Formation pass laterally into micritic limestones, marly limestones, and marls referred to as the Pilica Formation of Early Kimmeridgian age (Wierzbowski 2017).

In the area studied, Upper Jurassic deposits are truncated by erosional surface and the Pleistocene glacial and fluvioglacial sediments lie discordantly on various members of the Oxfordian—Kimmeridgian succession. Paleogene-Holocene erosion was controlled by the presence of fault zones (paleovalleys, modern rivers and karst valleys direction) and carbonate buildups within the Oxfordian sediments (Alexandrowicz and Alexandrowicz 2003). Lateral and vertical variations of lithologies within the durable carbonate buildups and surrounding weak deposits resulted in the formation of a number of erosive inliers (Matyszkiewicz and Krajewski 1996). The examples on the seismic data from the neighboring Miechów Trough show that the formation of biohermal structures can be driven by tectonics (Słonka and Krzywiec 2019). The carbonate buildups can also generate compactional system of discontinuous structures in their surroundings and overburden. Due to the positive relief of the terrain within the erosion-resistant carbonate structures, the large thickness of the Oxfordian formation can be observed not only within tectonic grabens but also within the uplifts (Matyszkiewicz et al. 2006).

Materials and methods

Materials

We used 121 boreholes that document three interfaces in the Kłobuck-Krzepice area (Fig. 1B): 1) the boundary between Quaternary and Upper Jurassic sediments (Fig. 2B), 2) the boundary between Oxfordian and Callovian sediments (Fig. 2C) and 3) the boundary between Częstochowa Ore-Bearing Clay Fm and Kościeliska Beds (Figs. 1C, 2D). The motivation behind selecting these interfaces is that they are inclined to NE at small angles, thus corresponding to the “layer-cake” assumption (Thiele et al. 2016). It was straightforward to calculate thicknesses representing: 1) Quaternary sediments, 2) Upper Jurassic sediments, and 3) Częstochowa Ore-Bearing Clay Fm + Callovian sediments (Fig. 3). The data set has been obtained from the Geological Company in Częstochowa. The majority of the geological documentation was completed during rapid exploitation of ore-bearing clays in the Wieluń-Częstochowa region in the 1950-1970s. The tectonic interpretation was performed after generating structural and thickness map and before the calculation of structural attributes (grid maps and angular distances). The faults striking parallel to the dip direction of the homocline were hypothesized on the basis of the curvature of the isolines on the structural maps (Fig. 2) and the accompanying rapid changes in the thickness on the isopach maps (Fig. 3). The faults striking perpendicular to the dip direction of the homocline were determined in most cases only on the basis of isopach maps.

Fig. 2
figure 2

Topography of the analyzed contacts with tectonic interpretation (elevation above sea level (m)): (A) The terrain surface, (B) A contact separating Quaternary sediments from Oxfordian sediments, note a closed form in southeastern part of the area, (C) A contact separating Oxfordian sediments from Callovian sediments, (D) A contact separating Częstochowa Ore-Bearing Clay Fm from Kościeliska Beds. Note that surfaces presented on C and D show a consistent subhorizontal dip to NE. The outcrops and quarries on the basis detailed geological map of the Polish – sheet Kłobuck (808) (after (Bednarek et al. 1992, modified) and Ostrowy (809) (after (Kaziuk and Nowak 2014, modified)

Full size image
Fig. 3
figure 3

Isopach maps of geological units separated by the considered surfaces with tectonic interpretation: (A) thickness of Quaternary sediments, (B) thickness of Oxfordian sediments, (C) thickness of Częstochowa Ore-Bearing Clay Fm and Callovian sediments. The outcrops and quarries on the basis detailed geological map of the Polish – sheet Kłobuck (808) (after (Bednarek et al. 1992, modified) and Ostrowy (809) (after (Kaziuk and Nowak 2014, modified)

Full size image

Triangulation

2D Delaunay Triangulation algorithm (De Berg et al. 2008) available in the CGAL (Yvinec 2021) library was used for the construction of triangulation based on the borehole data set (surface points). We note that the method can also be used for geophysical data sets (e.g., interpreted seismic horizons) for which usually much more data is available. We note that the 2D Delaunay triangulation is not unique if the input data set contains four points lying on a circle (De Berg et al. 2008). In such cases (common for geophysical data), if the data set contains many surfaces for angular distance measurements, then the generated triangulations may not be unique hindering the possibility of conducting relational measurements. In such cases, we propose to solve the non-uniqueness problem by producing only one triangulation for the entire data set (see Computer Code availability section)

Angular distance

We use the standard formula for calculating angular distance between planes (2-simplices) \(V\) and \(W\). If \(v\) and \(w\) denote the normal vectors of the planes \(V\) and \(W\), respectively, then the angle between \(V\) and \(W\) is calculated as follows.

$$arccos\frac{|v\cdot w|}{\Vert v\Vert \Vert w\Vert }$$
(1)

where \(|v\cdot w|\) is the absolute value of the dot product between vectors \(v\) and \(w\), and \(\Vert v\Vert \Vert w\Vert\) is the product of lengths of vectors \(v\) and \(w\).

We note that the analogous vertices of 2-simplices will share the same \(x\) and \(y\) coordinates and differ only respective to the \(z\) (elevation) coordinate. We illustrate the computational approach by the following example (also illustrated on Fig. 4).

Fig. 4
figure 4

Illustration of measuring angular distance between representative triangles of two geological surfaces. A single measurement involves two triangles: 1) representing the upper surface (red) and 2) representing the lower surface (blue). The angle is measured between normal vectors (yellow) of the respective triangles and the resulting value is then attached to the geometric centre of a “flat” (white) triangle determined by X and Y coordinates which are shared by two observational triangles (red and blue). To ensure comparability of the interfaces, we produce only one triangulation based on X and Y coordinates of all surfaces

Full size image

Example. Let \(P\) and \(R\) be planes documented by two triplets of points:\({p}_{1}\),\({p}_{2}\), \({p}_{3}\) and\({r}_{1}\),\({r}_{2}\), \({r}_{3}\):\({p}_{1}=\left[{x}_{p1},{y}_{p1},{z}_{p1}\right]=\left[\mathrm{1,0},1\right]\),\({p}_{2}=\left[{x}_{p2},{y}_{p2},{z}_{p2}\right]=\left[\mathrm{0,1},1\right]\), and \({p}_{3}=\left[{x}_{p3},{y}_{p3},{z}_{p3}\right]=\left[\mathrm{0,0},0.5\right]\) and\({r}_{1}=\left[{x}_{r1},{y}_{r1},{z}_{r1}\right]=\left[\mathrm{1,0},-0.5\right]\),\({r}_{2}=\left[{x}_{r2},{y}_{r2},{z}_{r2}\right]=\left[\mathrm{0,1},0\right]\),\({r}_{3}=\left[{x}_{r3},{y}_{r3},{z}_{r3}\right]=\left[\mathrm{0,0},0\right]\). Then, normal vectors of planes \(P\) and \(R\) as follows: \({n}_{p}=\left[-0.5,-\mathrm{0.5,1}\right]\) and\({n}_{r}=\left[\mathrm{0.5,0},1\right]\). The angle between planes \(P\) and \(R\) can be calculated as follows:

$$arccos\frac{|{n}_{p}\cdot {n}_{r}|}{\Vert {n}_{p}\Vert \Vert {n}_{r}\Vert }=arccos\frac{0.75}{\frac{\sqrt{6}}{2}\frac{\sqrt{5}}{2}}=56.79^\circ .$$

The resulting value can be attributed to the interior of a 2-simplex, and for convenience we attribute it to the geometric centre (Michalak et al. 2019, 2021). We note that in case of having \(n\) surfaces (interfaces), it is possible to create \(c\left(n\right)=\left(\begin{array}{c}n\\ 2\end{array}\right)=\frac{n\left(n-1\right)}{2}\) plausible comparisons, and \(n\ge 2\). For example, having 5 surfaces it is possible to create \(c\left(5\right)=\frac{5\left(5-1\right)}{2}=10\) comparisons (angular distance distributions). Likewise, it is possible to consider relationships between angular distance distributions, for example arithmetic differences between them (the motivation given in the Sect. "General description of measurements").

Log Transformation of angular distance

Given commonly observed near-log distribution of angular distance with many values close to zero and a positively skewed distribution, it is advisable to perform the log-transformation to check whether the transformation reduces the skewness and can better enhance variability in the data set (Limpert et al. 2001). However, we argue that it is beneficial to analyze the distribution of \({log}_{e}\left(x+1\right)\), where \(x\) is the original angular distance measures in degrees. Such a transformed distance will be referred to as log-distance. This proposition can be supported by at least three arguments: 1) the function \({log}_{e}\left(x\right)\) escapes quickly to minus infinity close to zero, and is in fact undefined for \(x=0\) (parallel planes – Fig. 5), 2) the function \({log}_{e}\left(x+1\right)=0\leftrightarrow {e}^{0}=x+1\leftrightarrow x=0\) (zero log distance implies zero distance of the original function), 3) the function \({log}_{e}\left(x+1\right)\) has always positive values for \(x\ge 0\), thus better resembles a distance which should be a positive value. We can also check the condition about the difference between log distances + 1 between surfaces (log distances + 1 are equal when the original distances are equal): \({log}_{e}\left(x+1\right)-{log}_{e}\left(y+1\right)=0\leftrightarrow {log}_{e}\left(x+1\right)={\mathrm{log}}_{e}(y+1)\leftrightarrow {e}^{log\left(y+1\right)}=x+1\leftrightarrow y+1=x+1\leftrightarrow y=x.\)

Fig. 5
figure 5

Comparison of ln(x) versus ln(x + 1) as candidates for a distance function. The values of the first function are negative for x < 1 and approach minus infinity when x approaches zero. The latter function takes zero at x = 0 and has always positive values. Note that x denotes the original value of the angular distance in degrees

Full size image

Statistical analysis

When performing the statistical analysis of the angular distances and log transformed angular distances, we have noticed that the normality assumption (which is necessary for a wide range of certain tests) is not satisfied. The bootstrap resampling method (Efron 1979) is helpful in this situation, as it does not have any strong distribution assumptions. The bootstrap method is based on resampling—n observations are drawn with replacement from the original sample. The result is a realization of the data set from which we can calculate realizations of any statistic of interest. For example, we can estimate the variance (measure of uncertainty in an estimate) of a parameter (e.g., mean) directly calculated from the sample. At the same time, the expected value of the drawn bootstrap estimations is the original sample mean. We then prepare a distribution using the set of the available samples and then resample \(B=5000\) realizations. We note that in general increases in \(B\) leads to increases in both the accuracy and computation time. For each realization of the data, we calculate a realization of the mean (in general, estimated parameter) from the realizations of the dataset. Then, we obtain the collection of \(B\) estimations of mean. This new “sample of mean estimators” behaves in a highly regular manner from the statistical viewpoint and enables us to draw more detailed conclusions than drawing them directly from the original sample (Davison and Hinkley 1997). In particular, it allows us to capture the uncertainty of estimation which is due to the limited size of the sample. To introduce the bootstrap 95% confidence interval for mean, we sort our \(B\) estimations of mean in ascending order, then consider the 2.5th and 97.5th percentiles of our data. These values are the lower and upper bound of our confidence interval, respectively.

Results

General description of measurements

We selected three geological interfaces to conduct measurements of angular distance between them: 1) interface between Quaternary and Oxfordian sediments (denoted as 0), interface between Oxfordian and Callovian sediments (denoted as 1), interface between Częstochowa Ore-Bearing Clay Fm and Kościeliska Beds (denoted as 2).

Table 1 shows the calculated basic statistics (e.g., sample mean, sample variance, bootstrap means and bootstrap 95% confidence interval for the means). These statistics refer to two groups of measurements:

  1. 1)

    Angular distances and log distances between the following pairs of interfaces: 0 and 1 (denoted as 01), 0 and 2 (denoted as 02) and 1 and 2 (denoted as 12).

  2. 2)

    Arithmetic differences for angular and log distances between the following pairs of relations: 02 values were subtracted from 01 (denoted as 01–02), 12 values were subtracted from 01 (denoted as 01–12), 12 values were subtracted from 02 (denoted as 02–12).

Table 1 Statistical results from measuring angular distances between interfaces (0 – interface between Quaternary and Oxfordian sediments, 1 – interface between Oxfordian and Callovian sediments, 2 – interface between Częstochowa Ore-Bearing Clay Fm and Kościeliska Beds, 01 – distribution between 0 and 1 interfaces, 02 – distribution between 0 and 2 interfaces, 12 – distribution between 1 and 2 interfaces) and comparing angular relationships (01–02 – arithmetic difference between 01 and 02 distributions, 01–12 – arithmetic difference between 01 and 12 distributions, 02–12 – arithmetic difference between 02 and 12 distributions)
Full size table

The motivation behind the second group of results is to compare conformability between two angular distance distributions if the data were collected from a common borehole network (Fig. 4). For example, one can calculate the angular distance between surfaces A and B to obtain the distribution AB. Then, one can calculate the angular distance between surfaces C and D to obtain the distribution CD. Then, it is possible to assess which relationship is more conformable by subtracting AB from CD. For example, if most of the AB minus CD values are positive, then one can interpret this result as follows: the relationship between A and B is less conformable than that of between C and D.

Angular distances and arithmetic differences

The calculated bootstrap 95% confidence intervals for means were greatest for the pairs of genetically unrelated relations: 01 and 02 ([1.482, 1.891] and [1.842, 2.488], respectively).Interestingly, for the genetically related horizons (separating only homocline-related Jurassic contacts) the calculated 95% confidence interval for the mean [0.951, 1.383] is smaller and does not overlap with any of the intervals calculated for the unconformable relationships (Fig. 6). This testifies to the expected result that the pairs of genetically related horizons indicate smaller within angular dissimilarities than the pairs of genetically unrelated horizons.

Fig. 6
figure 6

Angular distance distributions between compared surfaces. We calculated the 95% confidence interval (blue) for the mean (red). Note that the smallest values can be observed for the conformable relationship between contacts separating only Jurassic sediments (E and F)

Full size image

It can also be observed that for all cases the variances of the log(x + 1) distances were smaller (values were reduced from 2.376 to 0.214, from 6.094 to 0.309 and from 2.738 to 0.228, for 01, 02, and 12 distances, respectively – Table 1). This result, reflecting in fact the less dispersed data along with a smaller degree of skewness (Fig. 6B, D and F), suggests that the use of log(x + 1) distance can better enhance the relative variability of the originally skewed and more dispersed angular distance measurements (Fig. 6A, C and E).

Regarding the arithmetic differences (Fig. 7), we can see that for the genetically unrelated relationships the calculated 95% confidence interval for the mean is close to zero [-0.337, 0.094]. This result can be interpreted that the angular distance distributions 01 and 02 are very similar. However, this is not the case when the values of angular distance between genetically related horizons (12) are subtracted from the unconformable relationships (from 01 and 02). In this case, the 95% confidence intervals for the mean are positive and close to 1: [0.675, 1.381], [0.707, 1.308] for the arithmetic differences (01–12 and 02–12, respectively). This suggests that angular relationships between genetically unrelated interfaces are more unconformable than angular relationships between homocline-related interfaces. Likewise, for all cases the variances of the arithmetic log differences were smaller (values were reduced from 2.645 to 0.094, from 6.986 to 0.311 and from 5.119 to 0.242, for 01–02, 01–12, and 02–12 differences, respectively – Table 1).

Fig. 7
figure 7

Calculated difference of angular distance distributions. The mean value is in red while the median is in blue. Note that the mean and median values for the difference between: 1) relationship between surfaces of mixed origin and 2) relationship between surfaces belonging to the homocline (separating only Jurassic contacts) is positive (B and D). This suggests that the interfaces belonging to the homocline show in general a greater degree of angular similarity

Full size image

In some parts of the study area, we observe singular relationships between the spatial distribution of the angular distance and thickness. For example, west of the Biała Oksza river the following relationship is observed: 1) increasing (to NE) thickness of Oxfordian sediments (Fig. 3B) and 2) increasing values of angular distance (Figs. 8A, 9A). To interpret this result, we first note that a positive constant of angular distance between two surfaces is a sufficient condition to imply increasing thickness. However, because the angular distance is also increasing, this effect can be explained as the non-linear growth of thickness to NE (Figs. 8A, 9A).

Fig. 8
figure 8

A non-geostatistical modelling of angular distance using akima package: (A) between Quaternary-Oxfordian and Oxfordian-Callovian sediments, (B) between Quaternary-Oxfordian and Częstochowa Ore-Bearing Clay Fm-Kościeliska Beds, (C) between Oxfordian-Callovian and Częstochowa Ore-Bearing Clay Fm-Kościeliska Beds. Note that on the maps involving the Quaternary-Oxfordian interface there is an area of higher angular distance that corresponds to the closed form visible also in Fig. 2B

Full size image
Fig. 9
figure 9

Geostatistical modelling of angular distance: (A) between Quaternary-Oxfordian and Oxfordian-Callovian sediments, (B) between Quaternary-Oxfordian and Częstochowa Ore-Bearing Clay Fm-Kościeliska Beds, (C) between Oxfordian-Callovian and Częstochowa Ore-Bearing Clay Fm-Kościeliska Beds. Note that on the maps involving the Quaternary-Oxfordian interface there is an area of higher angular distance that corresponds to the closed form visible also in Fig. 2B

Full size image

Interpolation and Geostatistical Modeling

The results show (Figs. 8, 9, 10, 11 and 12) an elongated zone of increased angular distance common for all cases (latitude between 942000 and 948000 and longitude between 230000 and 235000). Interestingly, when considering the angular distance between genetically related interfaces, this zone is sub-divided into three parts. This internal repartition can be better observed on Fig. 12B (interface between Częstochowa Ore-Bearing Clay Fm and Kościeliska Beds) where a small-scale convex form can be observed which however cannot be observed on Fig. 12A (Oxfordian-Callovian interface). The effect of the more wavy geometry of the triangulated surface (Częstochowa Ore-Bearing Clay Fm/Kościeliska Beds) can be also observed on Fig. 13 where the trends of the red and green contour lines (Oxfordian-Callovian and Częstochowa Ore-Bearing Clay Fm-Kościeliska Beds interfaces, respectively) diverge in the central part of the analyzed zone. A second place of the increased angular distance can be observed in the south-eastern part of the analyzed area. There is a convex form developed in the Częstochowa Ore-Bearing Clay Fm-Kościeliska Beds interface (Fig. 12B) and a closed form in the Quaternary-Oxfordian interface which produces higher angular distance when the distance between these interfaces is analyzed (Figs. 8 and 9 AB). The higher values of angular distance could be also conceptualized as resulting from crossing blue and red contour lines representing Quaternary-Oxfordian and Częstochowa Ore-Bearing Clay Fm-Kościeliska Beds interfaces, respectively (Fig. 13).

Fig. 10
figure 10

Using akima package to calculate arithmetic difference between angular distances distributions. Note that the values for the relationship between surfaces belonging to the homocline (separating only Jurassic contacts) may be sometimes greater than the relationship between surfaces of mixed origin. This effect can be observed on Fig. 10B: blue places representing negative values

Full size image
Fig. 11
figure 11

Using geostatistical approach to calculate arithmetic difference between angular distances distributions. Note that the geostatistical modelling produced very smooth (high nugget value – see Figs.S2-S7 for comparison) models which makes it more difficult to conduct a spatial analysis

Full size image
Fig. 12
figure 12

A clustering orientation map (a grid map) with four manually created clusters for two interfaces with tectonic interpretation copied from Fig. 2. The partition has been created as follows: green – dip direction between 20 and 70 degrees with dip angle below 1.2 degree, black—dip direction between 20 and 70 degrees with dip angle more than 1.2 degrees, blue – dip direction between 70 and 225 degrees, red – dip direction between 225 and 20 degrees. Note that in the older interface (Fig. 12B) the area marked with a yellow ellipse lying to the West shows a greater number of alternating dip directions. The methodology of generating grid maps was described by Michalak et al. (2022) and in Supplementary Materials.

Full size image
Fig. 13
figure 13

A contour map with three contours representing three surfaces: blue – Quaternary/Oxfordian contact, green – Oxfordian/Callovian contact, red – Częstochowa Ore-Bearing Clay Fm-Kościeliska Beds contact. Two orange polygons show places where contour lines are crossing which produces higher values of angular distance. The orange polygon lying to the West shows an elongated form with differences in development for the three analyzed surfaces. The orange polygon lying to the East shows a closed form in the Quaternary/Oxfordian contact which is not developed in other contact surfaces

Full size image

Structural interpretation

We identified three sets of faults. The first set comprises faults that intersect only the Oxfordian and the top of the Callovian. It probably consists of syn-sedimentary faults, related to the presence of carbonate build-ups and varied compaction process. Due to the erosive nature of the Oxfordian top, these faults are highly hypothetical. The second set comprises faults that intersect the Oxfordian, Częstochowa Ore-Bearing Clay Formation and the top of the Kościeliska Beds. It consists of faults that were active or reactivated during Alpine orogeny movements in transpressional and transtensional stress field (narrow horst and grabens, oblique faults, horsetail-like elements). Due to the fact that they are also blind faults, the date of their latest activity remains unknown. It can be argued that some of them were active during the Middle Jurassic (Fig. 3C) or the Oxfordian (Fig. 3B). The third set comprises faults of Middle Jurassic age that intersect only the top of Kościeliska Beds and these faults were not reactivated (Figs. 2D, 3C).

Discussion

General discussion and limitations

Our method offers possibility to investigate the degree of parallelism between top and bottom of a geological unit. While potentially useful for detecting unconformities, it is not specifically designed for data sets with missing interfaces in boreholes. In fact, such an effect can likely be explained by an erosion or unconformity and our method is designed for data sets for which no preferential information of this kind is available.

In our method, it is key to distinguish the location of boundaries between units of strata from the location of strata comprising these units. These locations are not necessarily equal and this informs the type of unconformity (angular, erosional, paraconformity or onlap). Without additional measurements of strata it is impossible to identify the unconformity type.

Our method holds promise for identification of small structures that are reflected in geometry of only one of the two compared horizons (see a small-scale convex form on Fig. 12B). We urge caution about interpreting increased values of angular distance near faults as always resulting from bending of strata in the vicinity of faults. In fact, increased values of angular distance can also be observed for parallel surfaces with a specific spatial configuration of boreholes (Fig. 14).

Fig. 14
figure 14

A non-zero value of angular distance between triangles representing two parallel interfaces. This effect is due to a non-vertical fault and spatial configuration of boreholes. One of the boreholes passes through a fault plane causing also reduced thickness. We note that a symmetric effect would be possible on the right side of the setting with reverse orientations of the triangles: the upper triangle would be parallel to the horizon and the lower triangle would have a greater dip than that of the horizon

Full size image

Combinatorial complexity

As mentioned in the Introduction, the number of genetically related strata comprising a conformable succession may not always be known in advance and a user might want to conduct angular distance measurements within a greater (\(n>2\)) set of interfaces. We note that with increasing number of interfaces in the data set, obtaining the results may be more and more challenging due to combinatorial complexity. Let \(c\left(n\right)\) be the number of plausible comparisons (angular distance distributions) based on \(n\) surfaces, then it is possible to investigate \(c\circ c=c\left(c\left(n\right)\right)=\frac{c\left(n\right)\left(c\left(n\right)-1\right)}{2}=\frac{\frac{n\left(n-1\right)}{2}\left(\frac{n\left(n-1\right)}{2}-1\right)}{2}=\frac{1}{8}\left(\left(n-1\right)n-2\right)\left(n-1\right)n\) relationships between these distributions (e.g., differences between two distributions), where \(n\ge 2\) and \(c\left(c\left(2\right)\right)=0\) (having only two surfaces it is possible to create only one distance map which cannot be compared with any other distance map). Having 3, 5 and 10 surfaces it is possible to create 3, 10 and 45 angular distance distributions, as well as 3, 45, and 990 relationships between these distributions, respectively.

Triangle inequality—remarks

In this paragraph, we would like to stress the importance of triangle inequality for legitimacy of angular distance measurements. Suppose that the angular distance between two simplices \(V\) and \(W\) is equal to 20, and the angular distance between the simplex \(W\) and a simplex \(U\) is 20, but the angular distance between \(V\) and \(U\) is equal to 50: in other words, the direct angular distance between \(V\) and \(U\) is greater than the sum of indirect angular distances between \(V\) and \(W\) and between \(W\) and \(U\). That would mean, however, that the direct angular distance measured between \(V\) and \(U\) is not optimal, and should be replaced with the abovementioned sum of two indirect angular distances. But, of course, such a behaviour would jeopardize the sense of considering angular distances greater than 0. In order to rule out such an undesirable possibility, we need to verify that the angular distance is, in fact, a metric, that is a function \(d:X\times X\to \left[0,\infty \right]\) such that

$$\left(1\right) d\left(V,W\right)=0\leftrightarrow V=W$$
$$\left(2\right) d\left(V,W\right)=d\left(W,V\right)$$
$$\left(3\right) d\left(V,W\right)\le d\left(V,U\right)+d\left(U,W\right)$$

for all \(V\),\(U\) and \(W\) in \(X\). Here \(X\) denotes the set of all 2-simplices, and the condition (3), whose importance we discussed, is called the triangle inequality, a problem posed by (Michalak and Bytomski 2018) but still unsolved using a numerical justification. The positive answer to the triangle inequality problem is, however, given for more general context, i.e. for Hilbert spaces in the paper of Rao (Rao 1976).

Conclusions

  • We demonstrated a method to calculate angular distance distributions from among hundreds of borehole data documenting three contact surfaces. A major significance of the study follows from the fact that the parallelism assumption plays a significant role in subsurface 3D geological modelling.

  • The simultaneous presence of increasing thickness and angular distance in a specified direction can be explained by non-linear growth of thickness in this direction (the part of the study area west of the Biała Oksza river in Figs. 8A and 9A). This effect would not be straightforward to observe if only thickness variation was analyzed.

  • The workflow can reveal differences in geometry of analogous forms reflected in different surfaces. In particular, it can be sensitive to the detection of small-scale structures (Figs. 8C and 12B), thus potentially useful in reflecting geometric complexity in sparse environments (Caumon et al. 2009)

  • In our experiment, one surface separated Quaternary from Jurassic sediments, while the other two surfaces were members of the homocline in that they were gently inclined to NE and separated only Jurassic sediments (Oxfordian from Callovian and Częstochowa Ore-Bearing Clay Fm from Kościeliska Beds). In our case, the summary statistics of angular distances (mean) turned out to be smaller for the pair separating only Jurassic sediments. However, we identified also places for which the opposite is the case (Figs. 10 and 11).

  • Because triangulations are not unique if the data set considered contains four co-circular points (a potential issue for seismic data stored in regular grids), it is of vital importance to ensure that the triangulation is common for all surfaces. Otherwise, it can be argued that different triangulations pose the risk of any comparisons being illegitimate (incomparable unit observations). The comparability feature is ensured in our software which produces only one triangulation that is common for all \(n\) surfaces considered. Having these \(n\) surfaces it is then possible to create \(n(n-1)/2\) pairs of angular distance distributions.

  • The method is applicable as long as the definition of a terrain is satisfied. For example, if a borehole contains repetition of strata (two values of elevation for a considered interface), then the definition of a terrain does not hold and the method is not applicable.

  • The combinatorial complexity is a challenge especially when there is a further need to perform arithmetic operations (e.g., calculating difference) on the angular distance distributions. The parallelization of the computations may be a candidate solution to this problem.