Introduction

The mechanisms underlying biogeographic patterns of species diversity and community structure are among the most studied and debated questions in ecology (Lomolino et al. 2017). One prominent example is the area effect, where an increasing habitat size leads to an increasing number of coexisting species (MacArthur and Wilson 1967; Holt 1993). Spatial diversity patterns are also related to geographic constraints. According to the so-called mid-domain effect (MDE) in a spatial domain restricted by “hard boundaries,” species richness tends to peak at the center of the domain and declines towards the boundaries (Colwell and Hurtt 1994). “Hard boundaries” could be realized, for example, by continental edges or mountaintops for terrestrial species, shorelines for aquatic species, or any other large-scale dispersal barriers. The MDE occurs even in the absence of other environmental gradients, and is thus solely caused by spatial constraints.

The MDE is expected to occur by simple theoretic reasoning: Assuming a random distribution of species ranges within a bounded domain, in general, more ranges should overlap near the middle of the domain than at the edges, producing a peak or plateau of species richness towards the center. In a large number of empirical and theoretical investigations, the effect has been firmly validated and established as a null model for gradients in species richness (Willig and Lyons 1998; Colwell and Lees 2000; Bokma et al. 2001; Jetz and Rahbek 2001; Grytnes 2003; Connolly 2005). While the MDE was traditionally formulated for one-dimensional habitats, like latitudinal (Colwell and Hurtt 1994), elevational (Kessler 2001; Grytnes and Vetaas 2002), and bathymetric (Pineda and Caswell 1998) gradients or river courses (Dunn et al. 2006), two-dimensional extensions have been developed as well (Jetz and Rahbek 2001; Bokma et al. 2001). Despite its seminal role of describing species richness gradients, not much is known about how the MDE scales across trophic layers, raising the question for theoretical approaches to study spatially structured trophic communities.

One prominent classic approach to theoretically capture the dynamics and patterns of spatial communities is provided by the metapopulation framework (Levins 1969; Hanski and Gilpin 1991). The underlying principle is that an ensemble of local populations can be described by the dynamic balance between colonization of empty patches from occupied ones and local extinction of occupied patches, allowing a species to persist regionally despite the possibility of local extinctions. By augmenting this approach to metacommunities, Tilman (1994) showed that a potentially infinite number of competitors can regionally coexist, even if locally one superior competitor drives all other species to extinction. The precise spatial structure can affect species diversity in a metacommunity, as was shown in microcosm experiments on river-like spatial networks and lattice structures (Carrara et al. 2012, 2013). Thereby, the network structure affects patterns of population densities (Altermatt and Fronhofer 2018).

In a pioneering series of studies, Holt 1993, 1996, 2002 demonstrated that space can have similar effects in trophically interacting communities. In particular, he could show that in meta-food-webs species richness and food chain length should increase with increasing habitat size. Subsequently, metapopulation models based on colonization–extinction dynamics were developed to study the consequences of habitat destruction at different trophic levels (Bascompte and Solé 1998; Melián and Jordi Bascompte 2002). In another series of studies, Liao et al. 2017a, b, c) showed that habitat loss and fragmentation can have different effects on meta-food-webs and that, in particular, an intermediate level of fragmentation, compared to a strongly connected remaining habitat, can promote food web persistence. While these models treated only simple few-species food web motifs, recently, this approach was extended to include a larger number of species (Pillai et al. 2010, 2011; Calcagno et al. 2011; Gravel et al. 2011a, b). These studies showed that complex food webs can emerge at the regional scale even if locally only simple food chains are allowed. Based on these models, Barter and Gross 2016, 2017 highlighted the importance of the specific spatial structure of the habitat, for example, by explicitly embedding meta-food-webs in space in the form of random geometric graphs.

Many of these metacommunity studies that incorporate both trophic interactions and spatial structures are interested only in regional results, such as overall persistence or constraints on food web structure (Amarasekare 2008; Calcagno et al. 2011). In contrast, explicit spatial patterns of food web properties, such as spatial profiles of food chain length, and the contribution of spatial effects to their emergence, have rarely been considered or even quantified. This is astonishing, as food chain length is a central character of ecological communities and quantifies the number of feeding links between resources and top predators (Post 2002). Food chain length has classically been related to either dynamic constraints, where longer food chains become unstable and are particularly more vulnerable to perturbation, or to energetic constraints, where due to imperfect transfer of energy and resources a diminishing amount of energy is available to support higher trophic levels. Besides these two factors, the role of spatial constraints is increasingly recognized as a major determinant of food chain length (Post 2002). The main reasoning is that a larger area or ecosystem size should be able to support higher trophic levels and top predators. Nevertheless, model studies that predict spatial patterns of food chain length are still missing. In particular, to our knowledge, the MDE has never been formulated for food chain length.

In this paper, we study the role of geometric constraints for the formation of spatial gradients in trophically structured metacommunities. To this end, we develop a stochastic patch occupancy model including both trophic and explicit spatial structures. The model describes the colonization–extinction dynamics of a simple food chain on a network of habitat patches embedded in a one- or two-dimensional domain. By resolving results to individual patches, this setup allows us to investigate spatial patterns of food chain length, and to assess the role of the spatial constraints for the formation of these patterns. We intentionally choose a very simple model to ensure that we do not confound spatial effects with effects caused by more complicated food web dynamics. By combining direct stochastic simulations and analytic treatment in an ODE model, we calculate patch occupancies, persistence thresholds, and food chain length. Thereby, we consider different spatial scenarios: First, we study a spatially homogeneous or well-mixed system (representing high colonization rates or spatially implicit dynamics) and are able to show that food chain length increases with the square root of the ratio of colonization and extinction rates. Next, we study the influence of hard boundaries in one- and two-dimensional domains. We find that the patch occupancy decreases towards the edge of the domain for all species of the food web, even though this spatial decrease varies with the trophic level. As a consequence, we find that the average food chain length peaks in the center and declines towards the boundaries of a spatial domain, demonstrating a clear mid-domain effect of food chain length. This trophic mid-domain effect already arises in a one-dimensional domain, but it is most pronounced at the headlands in a two-dimensional domain. Our findings exemplify the role of geometric constraints for the formation of spatial gradients in trophically structured communities.

Methods

Model setup

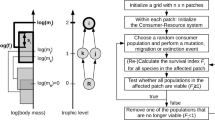
We develop a stochastic patch occupancy model to describe the colonization–extinction dynamics of a trophically structured community on an explicit spatial network of habitat patches (Fig. 1). Thereby, we follow Pillai et al. (2010, 2011); Gravel et al. (2011a), and Barter and Gross (2016, 2017) but restrict the trophic structure to a simple food chain. We assume that the network is embedded in a one- or two-dimensional domain. For any given patch, i = 1, ... , N, all patches within spatial distance up to the colonization range r are considered its neighbors, allowing colonizations between the patches. In the one-dimensional case, a patch that is not too close to any boundary has r neighbors to the left and r neighbors to the right. In the two-dimensional case, r is the radius of a circle. The colonization range influences the spatial structure as experienced by the species. The species in the food chain are labeled according to their trophic level by k = 1, ... , S, and we refer to the species at trophic level k simply by “species k.” In each patch, we track the presence and absence of all species. We call patches where species k is present k-occupied and where it is absent k-empty.

Fig. 1
figure 1

Conceptual diagram of the colonization–extinction model of a food chain on a network of habitat patches. Species (shown as orange circles) are aligned vertically according to their trophic level k = 1..S. Habitat patches (shown as rectangles) at spatial positions i = 1..N are aligned horizontally. All species that are present in a patch at this time point are indicated vertically above the corresponding rectangle. These species must form a contiguous chain starting at the lowest trophic level k = 1 (trophic interactions indicated as black vertical lines connecting the circles). Species can colonize neighboring patches within a colonization range r (black horizontal arrows). The green arrow indicates an exemplary colonization event of species 4 from patch 4 to patch 2. The dark-red cross indicates a possible extinction event of species 3 in patch 5 and the subsequent bottom-up extinctions of species 4 and 5 (light orange shading). Parameter values: S = 5 and r = 2

Full size image

We consider the case of “donor-controlled” stacked specialist food chains (Holt 1993, 1996). This means that a k-empty patch can be colonized by species k with a colonization rate c per k-occupied neighbor, but only if its prey species k − 1 is present on the target patch. If a patch is k-occupied, species k can go extinct with extinction rate e. In this case, all species higher up the chain go extinct as well at the same time instance. The basal species 1 suffers no such bottom-up extinction and has access to the full network. Furthermore, we neglect top-down extinction effects. Ecologically, this means that we assume that a predator does not over-exploit its prey and thereby increases its extinction risk.

For simplicity, we assume that the colonization rate c, the extinction rate e, and the colonization range r are the same for all species (i.e., being independent of the trophic level). This is not only a convenient simplification but also prevents confounding effects caused by differences between the species that go beyond their trophic positions. In all cases, we set the extinction rate to e = 1. This implies no loss of generality but simply fixes the time scale. Note that for a single species (S = 1), the model is equivalent to a susceptible–infected–susceptible (SIS) model from epidemics on networks (Pastor-Satorras and Vespignani 2001; Newman 2010).

Stochastic approach

We use two different approaches to analyse the model. First, applying a stochastic approach, we run the model based on direct stochastic simulations. Thereby, we use the Gillespie algorithm (Gillespie 1977) which simulates the dynamics step by step, one colonization, or extinction event at a time. Bottom-up extinctions are executed simultaneously with the primary extinction. The algorithm also provides the time that passes between any two processes, and thus produces a proper trajectory of the whole system. Quantities like food chain length or occupation probability of any species on any patch are calculated as time averages. When we are interested in these quantities resolved to single patches, we let the algorithm run for 100000 ⋅ S ⋅ N steps and calculate the time average over the last 90% of steps. When we are interested in spatial averages, which converge much faster, we let the system run for 100000 ⋅ S steps and, in addition to the spatial average, calculate the time average over the last 10% of steps. As initial conditions, we usually start with each patch having a probability of 0.5 to be occupied by the whole food chain. Using intensive numerical simulations, we have verified that our results on the equilibrium state are independent to variations of initial conditions, simulation and transient times, and averaging procedures.

Differential equation approach

Second, we employ a differential equation (ODE) approach to solve our model. Thereby, we model the occupation probability, \(u_{i}^{\left (k\right )}\), of species k on patch i in form of the following set of ordinary differential equations:

$$ \frac{\mathrm{d}u_{i}^{\left( k\right)}}{\mathrm{d}t}=c\left( u_{i}^{\left( k-1\right)}-u_{i}^{\left( k\right)}\right)\sum\limits_{j}A_{{ij}}u_{j}^{\left( k\right)}-{keu}_{i}^{\left( k\right)}. $$
(1)

Here, A is the adjacency matrix of the spatial network with Aij = 1 if patches i and j are connected and Aij = 0 otherwise. The second summand on the right-hand side of Eq. (1) describes the extinction of occupied patches (the factor k is necessary to include bottom-up extinctions). The first summand describes the colonization of empty patches and is given as the product of two terms. The first term \((u_{i}^{\left (k-1\right )}-u_{i}^{\left (k\right )})\) is the probability that species k is currently not present on patch i, but its required prey species k − 1 is present. In the equation for the basal species (k = 1), we set \(u_{i}^{\left (0\right )}=1\) meaning that the basal species has access to any patch of the network. The second term \({\sum }_{j}A_{{ij}}u_{j}^{\left (k\right )}\) is the expected number of k-occupied neighbors of patch i, taking into account that colonizers can only come from these patches. Equation (1) uses the approximation that these two quantities are independent. In reality, the probability that one patch is currently empty and that a given neighbor of this patch is currently occupied can be correlated (Newman 2010). Thus, we should expect the ODE model Eq. (1) to give only an approximation of the full dynamics, and we therefore always compare the solution to Eq. (1) with direct simulations of the stochastic model to verify the accuracy of this approximation.

Calculation of food chain length

Given our model, the food chain length Li on patch i can be obtained by simply counting the number of trophic levels. In the stochastic implementation of the model, we calculate this quantity directly for every patch and time instance, which then needs to be sufficiently averaged over time. In terms of the ODE model (1) and occupation probabilities \(u_{i}^{\left (k\right )}\), we calculate food chain length as the weighted sum of all possible food chain lengths (Holt 1993, 1996) as follows:

$$ \begin{array}{@{}rcl@{}} L_{i} & = & \sum\limits_{k=1}^{S} k \left( u_{i}^{\left( k\right)}-u_{i}^{\left( k+1\right)}\right) \\ & = & \sum\limits_{k=1}^{S}u_{i}^{\left( k\right)}. \end{array} $$
(2)

On the right-hand side of the first line in Eq. (2), \(u_{i}^{\left (k\right )}-u_{i}^{\left (k+1\right )}\) is the probability to find exactly the first k species, which follows from the hierarchical structure of the species. The food chain length is thus simply the sum of the occupation probabilities of all species in the food chain (Holt 1993; 1996).

Results

Patch occupancy and food chain length in a spatially homogeneous system

As a benchmark for the subsequent sections, we start by investigating a one-dimensional system with periodic boundary conditions. In this case, all patches of the lattice have the same number of neighbors, so that, after an initial transient, all patches will be equivalent for all times and the system becomes spatially homogeneous. In this case, the index i in Eq. (1) can be dropped and \({\sum }_{j}A_{{ij}}\) simply becomes a factor corresponding to the number of neighbors per patch, n(r). For the one-dimensional lattice, we have n(r) = 2r. With these changes, Eq. (1) becomes as follows:

$$ \frac{\mathrm{d}u^{\left( k\right)}}{\mathrm{d}t} = C \left( u^{\left( k-1\right)}-u^{\left( k\right)}\right)u^{\left( k\right)}-{keu}^{\left( k\right)}, $$
(3)

where we have defined the total colonization rate C = n(r)c. The probability \(u^{\left (k\right )}\) is now not only the probability that any given patch is k-occupied but simultaneously it is the expected fraction of k-occupied patches. For the basal species, Eq. (3) is essentially the same as the metapopulation equation introduced by Levins (1969). Note that due to neglecting spatial correlations, the equations for a closed lattice are the same as those for well-mixed space (Pillai et al. 2010; Calcagno et al. 2011; Gravel et al. 2011a).

Setting the right-hand side of Eq. (3) to zero, we find that the k th species has an equilibrium occupation probability of \( u^{\left (k\right )^{*}} = u^{\left (k-1\right )^{*}} - k (e/C) \) (Pillai et al. 2011). This can be solved to the following:

$$ u^{\left( k\right)^{*}}=1-\frac{e}{2C} k(k+1), $$
(4)

where negative values can be considered as equivalent to zero. As expected, species at lower trophic levels have higher occupation probabilities. This is shown in Fig. 2a, b for a food chain with S = 3 species, where we plot the expected fraction of occupied patches, \(u^{\left (k\right )^{*}}\), for each species as function of the total colonization rate C. Since for fixed C = 2rc, the occupation probability \(u^{\left (k\right )^{*}}\) does not depend on r, we obtain the same analytical results for r = 1 and r = 100. This is in striking contrast to direct simulations of the stochastic processes (marked symbols in Fig. 2a and b). While for r = 100, the analytical results from Eq. (4) coincide well with the stochastic simulation, for r = 1, the analytical results strongly overestimate the occupation probabilities. For a given species, this discrepancy between analytical and stochastic calculations decreases with increasing colonization rate and both approaches practically coincide for r ≥ 100.

Fig. 2
figure 2

Patch occupancy and food chain length in a one-dimensional lattice with periodic boundaries. a, b Equilibrium occupancies \(u^{\left (k\right )^{*}}\) of a three-species food chain as a function of the total colonization rate C = 2rc for r = 1 (a) and r = 100 (b). Solid lines: analytical results obtained by Eq. (4); discrete marker: stochastic simulation results, averaged over 50 repetitions for each value of r and C. c Stationary solution to the ODE model Eq. (3) for larger food chains. Black line: equilibrium occupancy u∗ as function of the trophic level k for C = 20, following the quadratic decrease from Eq. (4). Blue line: persistence threshold Ct as function of the trophic level k, following the quadratic increase from Eq. (5). d Dependence of food chain length on the total colonization rate C. Maximal possible trophic level \(k_{ {\max \limits } }\): exact result from Eq. (6) (black) and approximation \(k_{ {\max \limits } }\approx \sqrt {2C/e}-1\) (yellow). Average food chain length L: exact result from Eqs. (2) and (4) (blue) and approximation by Eq. (7) (red). The inset shows the dependency of L on C on a double logarithmic plot. To guide the eye, the black dotted line shows a power law \(L\sim C^{0.5}\). Parameter values: e = 1 and N = 1000 patches

Full size image

For both colonization ranges, for the stochastic as well as the ODE approach, and for all species, we observe a transition from a regime in which the species is extinct, \(u^{\left (k\right )^{*}}=0\), to a regime in which \(u^{\left (k\right )^{*}}>0\). The critical value \(C_{t}^{\left (k\right )}\) at which this transition occurs, the persistence threshold of species k increases with the trophic level. As seen from the stochastic simulation results in Fig. 2a, b, the persistence thresholds are larger for r = 1 than for r = 100. For example, \(C_{t,r=1}^{\left (1\right )}=3.2\), \(C_{t,r=1}^{\left (2\right )}=8.1\), and \(C_{t,r=1}^{\left (3\right )}=14.9\) compared to \(C_{t,r=100}^{\left (1\right )}=1.2\), \(C_{t,r=100}^{\left (2\right )}=3.2\), and \(C_{t,r=100}^{\left (3\right )}=6.4\). Again, for sufficiently large colonization range, the persistence thresholds obtained by direct simulation coincide with that from the ODE model.

By setting Eq. (4) to zero, we can calculate the persistence thresholds in analytic form, showing that the \(C_{t}^{\left (k\right )}\) increase quadratically with the trophic level as follows:

$$ C_{t}^{\left( k\right)}=\frac{{ek}\left( k+1\right)}{2}. $$
(5)

This is shown in Fig. 2c. For example, the sixth species in the food chain would be able to persist for a colonization rate of C/e > 21. Thus, with further increase of C an arbitrarily long food chain theoretically becomes possible. As further shown in Fig. 2c, the quadratic increase of the persistence threshold with k goes together with a quadratic decrease of the equilibrium occupancy. Thus, for C = 20, five species would be able to persist, while the occupation probability of the sixth species would be negative and thus zero. For a given value of the colonization rate, only a finite number of species can survive, even when potentially allowing an infinite number of species.

Finally, in Fig. 2d, we investigate the dependence of the food chain length on the colonization rate C. By setting Eq. (4) to zero and solving for k instead of C, we obtain the maximal trophic level, \(k_{ {\max \limits } }\), found in the system as follows:

$$ k_{ \max } = \text{floor} \left( -\frac{1}{2} + \sqrt{ \frac{1}{4} + 2 \frac{C}{e}} \right) , $$
(6)

which increases as \(k_{ {\max \limits } } \approx \sqrt {2C/e}-1\) for large C. This maximal possible length of a food chain in the system is larger than the average food chain length, L, because locally species continuously go extinct, yielding a reduction of the average food chain (blue line in Fig. 2d).

Using Eq. (2) and summing up the terms in Eq. (4) from k = 1 to the upper bound \(k_{ {\max \limits } }\approx \sqrt {2C/e}-1\), we can approximate the average food chain length as follows:

$$ L\approx \frac{2}{3} \sqrt{\frac{2C}{e}} -1 . $$
(7)

Thus, the average food chain length roughly scales with the square root of the ratio of colonization and extinction rates. This power law increase with C is superposed by slight irregularities at the persistence thresholds (see Fig. 2d). Note that this result, the quadratic decay of patch occupancy with C in Eq. (4) is in contrast to a previous estimation of the food chain length L ≤ C/e + 1 (Gravel et al. 2011a). These authors, however, did not consider bottom-up extinctions.

Trophic mid-domain effect in a one-dimensional domain

Next, we investigate the influence of hard boundaries in a one-dimensional lattice. For this, we simulate the dynamics of a food chain (with an in principle arbitrary number of species) on a one-dimensional lattice with N = 1000 patches and hard boundaries. We are interested in the spatial profile of occupation probabilities of all surviving species, and the resulting food chain length, resolved to individual patches. As before, we parametrize our model by the total colonization rate C = n(r)c, but for a lattice with hard boundaries, we define n(r) as the number of neighbors of a non-boundary patch. In the simulations, we pay specific attention to the total colonization rate C = 20, but repeated the simulations for a large range of C values. Our simulation runs, shown exemplary in Fig. 3, confirm that for sufficiently large colonization range (r = 100), we obtain an excellent agreement between the ODE approach and stochastic simulations also in the spatially explicit non-homogeneous system, similar to the case of a spatially homogeneous system (Fig. 2) where we used spatial averages.

Fig. 3
figure 3

Trophic mid-domain effect and spatial profile of food chain characteristics in a one-dimensional lattice with hard boundaries. a Equilibrium occupancy u∗ as a function of patch number for different trophic levels, from k = 1 (blue) to k = 5 (green), obtained from numeric simulation of the ODE model, Eq. (1). Since the solution is spatially symmetric, only the left part (patches 1 to 400) is shown. b Corresponding food chain length L, obtained from the ODE model (blue line) and from temporally averaged stochastic simulations (red dots). The horizontal black solid line marks the 95% value between \(L_{ {\min \limits } }\) and \(L_{ {\max \limits } }\) (see Eq. 9) and the solid vertical line marks the corresponding edge length E. The dashed vertical line marks the colonization range r. Note that the figure shows time-averaged quantities; a snapshot of a corresponding stochastic simulation is shown in Appendix A, Fig. 6. Parameter values: number of patches N = 1000, colonization range r = 100, total colonization rate C = 20, extinction rate e = 1

Full size image

In a homogeneous system, we found that for a total colonization rate of C = 20, a number of S = 5 species are able to persist (Fig. 2d). As shown in Fig. 3, this result holds true also in a one-dimensional lattice with hard boundaries (see also Appendix A, Fig. 6, showing a characteristic spatial profile from the stochastic model). Additionally, we observe a clear MDE: All species show a clear plateau in the inner parts (mid-domain) of the lattice and decay in occupation probability towards the boundary. The transition from the plateau to the boundary occurs roughly at patch r, though the transition is less sharp for higher trophic levels. On the other hand, the MDE is more pronounced for species at higher trophic levels that have overall smaller occupation probabilities. Since according to Eq. (2), food chain length is the sum of the occupation probabilities of all species, the food chain length must inherit the MDE pattern from the single species. Figure 3b confirms that this is indeed the case. Both ODE and stochastic simulations reveal a clear MDE for food chain length, meaning that food chain length also reaches a plateau value in the middle of the domain and decreases towards the boundary.

To characterize the trophic MDE, we first measure the maximal average food chain length \(L_{ {\max \limits } }\) within the plateau in the interior of the lattice and the minimal average food chain length \(L_{ {\min \limits } }\) at the boundary of the lattice. Based on these values, we define the relative strength of the trophic MDE as follows:

$$ R_{L}=\left( L_{ \max }-L_{ \min }\right)/L_{ \max } . $$
(8)

In general, this index measures the relative magnitude of the decay of the food chain length towards the boundaries. It is bounded by 0 ≤ RL ≤ 1 and larger values indicate a stronger spatial decay. For the example, shown in Fig. 3, we obtain the values \(L_{ {\min \limits } }=2.38\) and \(L_{ {\max \limits } }=3.25\), yielding a trophic MDE strength of RL = 0.27. Note that \(L_{ {\max \limits } }\) does not give the maximum number of species or trophic levels that can persist in the middle of the lattice (that would be S = 5 in this example), but instead gives the maximal value of the expected food chain length (see previous subsection).

While the index RL measures the “vertical” aspect of the trophic MDE in Fig. 3, we next define a measure for the “horizontal” aspect, that is, the characteristic spatial scale of the trophic MDE. For this, we define the edge length E as the distance to the boundary at which the food chain length reaches the level as follows:

$$ \begin{array}{@{}rcl@{}} L_{E} & = & \ L_{ \min }+0.95 (\ L_{ \max }-\ L_{ \min }) \\ & = & 0.05 \ L_{ \min }+0.95 \ L_{ \max } , \end{array} $$
(9)

that is, the level at which the food chain length has increased from its boundary value \(L_{ {\min \limits } }\) by 95% of its range between \(L_{ {\max \limits } }\) and \(L_{ {\min \limits } }\). For the example shown in Fig. 3, we find E ≈ 150 which is in the same order as the used value of the colonization range r = 100. Thus, the colonization range defines a characteristic spatial scale of the trophic MDE and approximately separates the plateau from the boundary regime over which the food chain length declines.

Next, we explore the dependence of the trophic MDE indices on the total colonization rate C. This is shown in Fig. 4 for maximal and minimal food chain length, \(L_{ {\max \limits } }\) and \(L_{ {\min \limits } }\), the relative trophic MDE strength RL, and the normalized edge length E/r. As expected from Fig. 2, \(L_{ {\max \limits } }\) and \(L_{ {\min \limits } }\) increase with increasing C (Fig. 4a). Since \(L_{ {\max \limits } }\) increases faster, the absolute strength of the trophic MDE, \(L_{ {\max \limits } }-L_{ {\min \limits } }\), is an increasing function of C as well. The relative strength, RL, on the other hand, on average is a decaying function of C (Fig. 4b). The trophic MDE is thus stronger for longer food chains in absolute numbers, but weaker on a relative scale.

Fig. 4
figure 4

Several trophic MDE quantifiers as functions of the total colonization rate C on a one-dimensional lattice (N = 1000 patches, hard boundaries, colonization range r = 100). Dashed vertical lines mark the persistence thresholds \(C_{t}^{\left (k\right )}\) of species 1 ≤ k ≤ 7 (see Eq. (5)). For \(C<C_{1}^{\left (k\right )}\), no food chain exists. Most quantities show an irregular behavior at the persistence thresholds. a Plateau chain length \(L_{ {\max \limits } }\) (black) and boundary chain length \(L_{ {\min \limits } }\) (blue). b Relative trophic MDE strength RL (black) and edge length normalized by colonization range E/r (blue)

Full size image

As shown in Fig. 4b, the relative edge length is largest at the persistence threshold of the first species at which the food chain starts to exist. For increasing C, the edge length has a decreasing tendency, though this tendency is superposed by an oscillating pattern, where typically minima of E/r arise at the persistence thresholds of additional species. The magnitude of these irregularities decreases with increasing C since the effect of a newly persistent species is weaker the more species are already present in the community. The relative edge length roughly converges to E/r ≈ 1.5 which is also the value that we found in Fig. 3. In Appendix B, Fig. 7, we elaborate on the dependence of the edge length E on the colonization range r. We find that for increasing r, food chain length \(L_{ {\max \limits } }\) and \(L_{ {\min \limits } }\) quickly converge to the values already observed in Fig. 3 (\(L_{ {\max \limits } }\to 3.25\) and \(L_{ {\min \limits } }\to 2.38\)) (Appendix B, Fig. 7a). For sufficiently large r (≳ 30), the edge length becomes a linear function of the colonization range, E ≈ 7.2 + 1.5r (Appendix B, Fig. 7b). From a theoretical point of view, these results imply that r (if not too small) primary serves as a spatial scale while relevant results (\(L_{ {\max \limits } }\), \(L_{ {\min \limits } }\) and E/r) are independent of r. This underlines the role of C being essentially the only free parameter in the system and justifies why we usually consider the ratio E/r.

Similar to the irregularities observed in Fig. 4, also in Fig. 7 in Appendix B, we can observe irregularities in the behavior of \(L_{ {\max \limits } }\), \(L_{ {\min \limits } }\) and E, in the regime of small r. These irregularities occur exactly at the “persistence thresholds” of the fourth and fifth species. The term “persistence threshold” is here not meant with respect to the total colonization rate C but with respect to the colonization range r. For r < 11, only four of the five species are able to persist. For r < 3, the fourth species goes regionally extinct as well. Even though the total colonization rate is constant, a large colonization range has a stabilizing effect on the food chain. This can be understood by acknowledging that for larger r, the effective distance between patches becomes smaller and that there are more alternative paths from one patch to another. For small r, the dynamics are less robust and local extinctions do more often lead to regional extinctions. Note that we have already seen this effect in Fig. 2a and b, where for r = 1, the persistence of any species required a significantly larger colonization rate than for r = 100.

We can calculate \(L_{ {\max \limits } }\) and \(L_{ {\min \limits } }\) analytically, by directly solving the set of equations (1) with an approximate ansatz. To this end, we use a continuous limit of Eq. (1) as follows:

$$ \frac{\mathrm{d}u^{\left( k\right)}\left( x\right)}{\mathrm{d}t} = c\left( u^{\left( k-1\right)}\left( x\right)-u^{\left( k\right)}\left( x\right)\right) {\int}_{\max\left\{ 0,x-r^{\prime}\right\} }^{\min\left\{ 1,x+r^{\prime}\right\} }u^{\left( k\right)}\left( y\right)\mathrm{d}y-keu^{\left( k\right)}\left( x\right). $$
(10)

Here, the discrete patches are replaced by continuous space (i → x, j → y) and the sum over i’s neighbors is now an integral over x’s colonization range, which is \(x\pm r^{\prime }\) if we are not too close to the boundary. The total habitat is normalized to be of unity length. In order to use the same range-to-habitat-size ratio as before (r = 100, N = 1000), we set the normalized colonization range to \(r^{\prime }=0.1\). To find the equilibrium occupation probabilities \(u^{\left (k\right )^{*}}\left (x\right )\), we set the left-hand side of Eq. (10) to zero. The resulting set of equations for different trophic levels k has to be solved iteratively, since the equation for species k depends on the solution for species k − 1. Only the basal species depends on no other species. To solve the integral in Eq. (10), we assume for each single \(u^{\left (k\right )}\left (x\right )\) a linear growth from the boundary value \(u_{ {\min \limits } }^{\left (k\right )}\) to the plateau value \(u_{ {\max \limits } }^{\left (k\right )}\) over an edge of length \(r^{\prime }\). In Fig. 3b, we have seen that this approximation is not entirely correct. But incorporating more details into the calculation (e.g., replacing the range r by our previous definition of the edge length E) does not improve the result. We therefore prefer to employ the simpler approach that only depends on qualitative observations instead of quantitative results. Within our approximation, it is straightforward to solve the integral in Eq. (10). By further using Eq. (2), we obtain for C = 20 the analytical food chain length results \(L_{ {\min \limits } }^{\text {ana}}=2.38\) and \(L_{ {\max \limits } }^{\text {ana}}=3.25\) which coincide with the values extracted from Fig. 3b.

Trophic mid-domain effect in a two-dimensional domain

Finally, we explore whether the results from the previous sections hold also in a two-dimensional domain. For this, we repeated the ODE simulations for the case C = 20 on a two-dimensional square lattice (N = 32 × 32 = 1024 patches) and on a two-dimensional lattice placed on the mainland of Australia (N = 2801 patches). For the colonization range, that is now a radius, we used r = 8. This amounts to n(r) = 196 neighbors (roughly πr2 ≈ 201) for any central patch that is not too close to any boundary. The connectivity of the networks is thus comparable to our choice in the one-dimensional case with n(r) = 200 for a colonization range of r = 100. We considered again hard boundaries and were interested in the food chain length resolved to individual patches.

Our numerical simulation (Fig. 5) demonstrates that the trophic MDE emerges also on spatial networks embedded in two-dimensional space. In fact, the effect in two dimensions is even more pronounced than in the one-dimensional case. For the relative strength of the trophic MDE, we find RL = 0.45 for the square lattice and RL = 0.64 for the lattice placed on the mainland of Australia (for the one-dimensional lattice it was RL = 0.27). We used a total colonization rate of C = 20 in all cases so that the results can be properly compared, and differences are caused only by the different spatial structures.

Fig. 5
figure 5

Trophic mid-domain effect in a two-dimensional domain. The figure shows the patterns of food chain length on a two-dimensional square lattice (aN = 32 × 32 patches) and an analogous lattice placed on the mainland of Australia (b N = 2801 patches). In both cases, we used hard boundaries, colonization range r = 8 as depicted by the circles, and total colonization rate C = 20. On both networks, food chain length shows a clear trophic MDE, with the largest value attained at the center. The respective minima are attained at the corners (square lattice), and at the north-eastern land tongue marked by the arrow (Australia)

Full size image

Using the same total colonization rate implies that we should find the same maximal chain length in all cases. For the example shown in Fig. 5, we find that this is true at least approximately (\(L_{ {\max \limits } }=3.22\) for the square lattice and \(L_{ {\max \limits } }=3.24\) for Australia compared to \(L_{ {\max \limits } }=3.25\) for the one-dimensional lattice). The reason for the small differences is related to the total extension of the domains, used in the simulation. In our finite two-dimensional networks, a larger fraction of patches belongs to the boundary and a smaller fraction belongs to the mid-domain. As a result, the lattice size is too small to support a true mid-domain plateau. We repeated the simulations for larger networks with a larger mid-domain to boundary ratio (i.e., having more patches but the same value of r) and found that the maximal food chain length indeed increased to \(L_{ {\max \limits } }=3.25\) for both two-dimensional structures.

The differences in the relative strength RL, observed in different network topologies, are caused by differences in the minimal chain length \(L_{ {\min \limits } }\). For the square lattice, we observe \(L_{ {\min \limits } }=1.77\) at the outmost corners, and for Australia, we find \(L_{\mathrm { {\min \limits } }}=1.17\) at the north-eastern land tongue marked by the arrow in Fig. 5. Note that in the one-dimensional case, we had \(L_{ {\min \limits } }=2.38\).

Discussion

In this study, we calculated the colonization–extinction dynamics of a food chain in spatial networks of different topologies. Our most notable finding is the mid-domain effect for food chain length, stating that food chain length is maximal in the center of a habitat and declines towards the boundaries, even in the absence of other environmental gradients. The effect can instead be explained as a direct consequence of the underlying spatial structure. Habitat patches close to the boundary have a smaller number of neighbors, and thus receive fewer incoming colonizations. Since outgoing colonizations do not take away anything from the source patch, and since extinctions are purely local events, having fewer neighbors has no other counteracting positive effects. A fewer number of neighbors thus leads to smaller species occupation probabilities and consequently to shorter food chains.

Food chain dynamics in a spatially homogeneous system

Our findings corroborate the theory that purely spatial dynamics can provide a constraint on maximal food chain length (Holt 1993, 1996). More generally, we found that even on spatially homogeneous habitats (that have periodic boundaries), the persistence and occupation probabilities of all species in the chain (and consequently also the food chain length) strongly depend on the colonization range r. A larger colonization range makes spread and persistence easier for all species. This happens even when the per-neighbor colonization rate is simultaneously decreased in such a way that the total colonization rate C remains constant. This can be understood by the following two arguments: (1) For all species, a larger colonization range (i.e., shorter path lengths between patches) means that empty patches can typically be (re)colonized faster (see also Barter and Gross (2017)). This increases robustness against local extinctions. (2) For species at higher trophic levels, we can further interpret the colonization range as the species’ ability to traverse through unsuitable habitat patches, where the required prey species is absent. For small ranges, the remaining suitable patches are more likely to be disconnected, which strongly diminishes the species’ colonization ability.

It was also for small colonization ranges (r = 1) that results of the stochastic and the ODE approach differed significantly, which can be understood as follows: For small ranges, the slow step-wise propagation of a species through the habitat network implies that occupied patches tend to form clusters, i.e., lie next to each other. This leads to strong correlations between the occupation status of adjacent patches; see also Newman (2010). For larger values of the colonization range, these correlations are much weaker, first since there exist much more alternative paths through the network and second because the average distance between patches is much shorter. For this reason, the agreement between the ODE approach, that neglects these correlations, and the stochastic approach, that contains these correlations, improves with larger colonization ranges (Fig. 2a and b). Note that it is possible to augment the ODE approach to partially include the correlations. This would require, however, additional and more complex equations, at the same time still being only an approximation (Newman 2010).

In the ODE approach used here, a lattice with periodic boundaries is formally equivalent to a well-mixed space. To actually obtain a well-mixed space from our one-dimensional lattice with periodic boundaries, we could use a colonization range r ≥ N/2. In Eq. (3), the colonization range does, however, enter only implicitly via the number of neighbors per patch, n(r), which is absorbed into the total colonization rate C. Accordingly, Eq. (4) shows that in equilibrium the fraction of occupied patches depends only on C, and not explicitly on the range r. The structure of the spatial network does also not enter the equation in any other way. This means that in our ODE approach, we obtain the same results for r = 1, an actual lattice with only next-neighbor interactions, and for r ≥ N/2, i.e., a well-mixed space.

We found that the fraction of occupied patches decreases with trophic level (see Eq. (4) and Fig. 2a, b, and c). This result is not surprising and has already been observed, e.g., by Pillai et al. (2011). It is simply a consequence of the fact that species at higher trophic levels can make fewer colonizations, as they are restricted to patches where their prey is present, and go extinct more frequently due to bottom-up extinctions. Both effects inhibit the spread of the species. The increase of the persistence threshold with trophic level (see Eq. (5) and Fig. 2d) is then simply a consequence of the decrease of the occupation probabilities. As another remarkable result, we found that the average food chain length roughly increases with the square root of the ratio of colonization and extinction rates. This result deviates from previous estimation of the food chain length (Gravel et al. 2011a) which, however, did not consider bottom-up extinctions.

The mid-domain effect for food chain length

We want to stress again that the MDE for food chain length, as explained above, emerges in the absence of any environmental gradients, except for the existence of the boundaries; it is solely caused by spatial constraints and can thus be considered a null expectation for spatial patterns of food chain length. Thereby, the MDE is not supposed to fully explain an actually observed pattern, such as food chain length or (traditionally) species richness. The MDE should rather be part of a multivariate explanation (Colwell and Lees 2000; Jetz and Rahbek 2002; Colwell et al. 2004). Other factors potentially contributing to observed spatial patterns are heterogeneities in temperature, productivity, annual precipitation, habitat diversity, or even “historical gradients” like time since the last glaciation; see, for example, Colwell et al. (2004) and Jetz and Rahbek (2002) and references therein. This is in particular true for our illustrative example using the mainland of Australia (Fig. 5b), where food chain length pattern are likely to be strongly influenced by the existing environmental gradients. We also want to point out that, while there is no environmental gradient (other than the boundary) as input to our model, the model generates its own gradients for species at higher trophic levels (see Fig. 3a). The mid-domain pattern of the occupation probability of the basal species is solely caused by the spatial constraints. Due to the dependence of higher trophic levels on lower ones, the patch occupancy of a higher level is additionally influenced by the occupation pattern of the next lower one. In this way, the MDE cascades up the food chain, being stronger for species at higher trophic levels and finally leading to a significant MDE for food chain length.

The mechanistic explanation of the MDE for food chain length, as presented here, slightly deviates from the classic explanation of the MDE for species richness. The MDE is classically explained by randomly placing species ranges into a large region (Colwell and Hurtt 1994; Colwell and Lees 2000; Jetz and Rahbek 2001). The mid-domain peak or plateau of species richness then emerges since the centers of these ranges must not lie too close to the boundary in order to not overlap with the inhabitable zone. This theory, even though being very compelling, is not sufficient to explain a trophic MDE. In this framework, it is not sufficient that the richness at all trophic levels decline towards the boundary. An MDE for food chain length, i.e., a decline in the number of trophic levels towards the boundary, can only arise if the richness at higher trophic levels decline more rapidly than that at lower trophic levels. To obtain this, we would need to require that species ranges increase with the trophic level, which however seems not to be supported by empirical evidence. While a scaling with body mass, and thus with trophic level, has been well established for the home range of a species, i.e., the area or territory in which an individual animal lives and moves on a periodic basis (Jetz et al. 2004), there is no evidence that the same holds true for the species range, i.e., the full geographic area where all individuals of a particular species can be observed (Gaston 1996).

In addition, there are several noteworthy differences between the MDE for food chain length and the classical MDE for species richness as described by Colwell and Hurtt (1994): (i) Classically, species ranges span only over a fraction of the totally available habitat. In contrast, in our case, species span over the full habitat, but in the absence of any additional factors that shape occupation patterns, this result is only natural. (ii) Classically, MDE models describe cohesive species ranges (but for exceptions, see for example (Grytnes and Vetaas 2002; Dunn et al. 2006)), whereas in our case, at a given point in time, species ranges are highly fragmented (see Appendix A, Fig. 6). Only at the level of expected values, i.e., time averages, do species ranges appear to be continuous. Note that in real data, the fragmentation might be caused by various factors, such as undersampling, environmental heterogeneity (unsuitability of certain regions), but also by actual breaks in species ranges (Dunn et al. 2006). (iii) Classically, species richness declines to zero at the boundary (but for exceptions, see for example, (Jetz and Rahbek 2001; Grytnes and Vetaas 2002)), whereas in our case, food chain length declines to non-zero values at the boundary.

Even though the MDE for species richness has been subject to criticism (Bokma et al. 2000; Laurie and Silander 2002; Colwell et al. 2004), there is a large consensus that boundary constraints affect spatial patterns of species richness at least to some degree. The same should be true also for patterns of food chain length. Thus, we expect that an MDE for food chain length will also be observed when changing details of the model, or when using an entirely different one, as long as spatial constraints are included. Spatial constraints should thus always be considered as one possible explanatory factor for spatial patterns of food chain length (or any other ecologically interesting quantity).

Some diversity gradients that have classically been explained by the MDE for species richness span large spatial scales (e.g, ranging over thousands of kilometers) which can easily exceed the spatial scale of metacommunities and dispersal. Not surprisingly, patterns of species richness were found to be less effected by geometric constraints for species with smaller spatial ranges (Jetz and Rahbek 2001; Dunn et al. 2006; Dunn et al. 2007). Similarly, the trophic MDE might only weakly contribute to patterns of food chain length for species with a small colonization range relative to the domain size, since in this case the plateau of the food chain length reaches much closer towards the habitat boundaries (Fig. 7b). Conversely, the trophic MDE might best explain patterns of food chain length observed along elevational or bathymetric gradients or river courses that span shorter geographic distance. Thus, the relative effect of food chain dynamics for describing MDEs should strongly depend on taxa, because a distance that is exceptional for plants and mammals, could play a lesser role for birds and marine fauna (Kinlan and Gaines 2003).

We observed that the trophic MDE characterized by its relative strength RL is stronger for two-dimensional habitats (e.g., \(R_{L}^{\left (2d,\text {Australia}\right )}=0.64\) and \(R_{L}^{\left (2d,\text {square}\right )}=0.45\)) than for the one-dimensional lattice (e.g., \(R_{L}^{\left (1d\right )}=0.27\)). This observation is in agreement with our general explanation of the MDE for food chain length in our model, i.e., that the trophic MDE is caused by the fewer number of neighbors of boundary patches compared to central patches. The larger this difference becomes, the stronger the trophic MDE should be. The ratios of the number of neighbors of the outmost boundary patches to central patches, nbound, were \(n_{\text {bound}}^{\left (1d\right )}=0.5\), \(n_{\text {bound}}^{\left (2d,\text {square}\right )}=0.29\), and \(n_{\text {bound}}^{\left (2d,\text {Australia}\right )}=0.16\). As expected, the decreasing tendency of nbound matches the increasing tendency of RL. More generally, this suggests the perimeter-to-area ratio as a key feature of habitat configuration determining the strength of trophic MDE in two-dimensional domains.

Empirical support and further considerations

In this study, we were mainly concerned with a theoretic exploration of the MDE for food chain length, and we leave it as a challenge for future work to test our theoretic predictions in field data. One simple reason for this focus of our study is that empirical data on spatial food web structure are hard to come by. While topological aspects for food webs at single patches have been characterized in depth (Thompson et al. 2012), data on spatial food web structure are scarce. Nevertheless, there are empirical observations that suggest an MDE for food chain length. For example, it has been well established in fisheries that large top predatory fish are dominantly observed in mid ocean, but are rarely observed in coastal areas (Worm et al. 2003). In another study, Komonen et al. (2000) observed that a food chain consisting of the bracket fungus Fomitopsis rosea, the tineid moth Agnathosia mendicella, and the parasitic tachinid fly Elfia cingulata reduced to the first one or two trophic levels in isolated forest fragments. For more complex spatial structures, it becomes more difficult to classify patches into boundary and central or isolated and non-isolated patches. In fact, a continuous “degree of connectedness,” in network theory known as centrality measures (Newman 2010) is needed to properly characterize patches. For our lattices, we simply used the distance to the boundary as such a measure, but for more complex networks, the choice of centrality measure is less straightforward. Properly quantifying and predicting spatial patterns of food chain length on arbitrary habitat networks could thus prove challenging.

In general, not only the spatial structure but also the food web structure will be more complex than studied here. One interesting avenue for further explorations would be to extend this analysis to the spatial patterns of other food web properties beyond food chain length, such as connectance or food web branching (Martinez 1991; Thompson et al. 2012). In our spatial setting, the mechanism causing the trophic MDE, i.e., the smaller number of neighbors in boundary patches, is rather generic and does not depend on the food web structure or the nature of the trophic interactions. More complex food webs and top-down effects could, however, have additional effects that might alter the mid-domain pattern. For example, the decrease of the occupation probability of one species towards the boundary could open a niche for other species better adapted to this range, but that are out-competed in the mid-domain. Such community effects might well lead to more complex spatial profiles, possibly yielding even an inverted mid-domain pattern. Another top-down effect with the potential to feed back on the spatial structure is the predator-mediated coexistence of multiple prey species (Holt 1984), meaning that each new trophic level potentially allows more species in lower trophic levels to coexist. Thereby, the larger number of trophic levels in the mid-domain could locally increase the number of species per trophic level, and thus amplify the absolute gradient in species richness, essentially propagating the MDE in food chain length to an enhanced MDE in species richness.