An eco-evolutionary system with naturally bounded traits

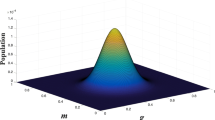
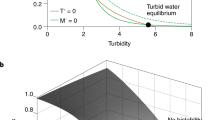
Abstract

We consider eco-evolutionary processes that include natural bounds on adaptive trait distributions. We implement ecological axioms, that a population grows if it is replete with resources, and doesn’t grow if it has none. These axioms produce natural bounds on the trait means that suggest that the assumption of gamma-distributed traits, where the trait variance is a function of the trait mean, is more appropriate than the usual assumption of normally distributed traits, where the trait variance is independent of the trait mean. We use a Lotka-Volterra model to simulate two plant populations, whose trait means evolve according to an evolutionary model, to simulate populations adapting during invasions. The results of our model simulations using gamma-distributed traits suggest that adapting populations may endure bottlenecks by increasing their fitness and recovering from near extinction to stably coexist. The inclusion of eco-evolutionary processes into ecosystem models generates K^∗ theory which predicts the long-term states of populations that make it through evolutionary bottlenecks. Otherwise, the final states of populations that do not make it through bottlenecks may be predicted by the non-evolutionary R^∗ theory.

Appendix: Traits with bounded distributions

The bounds upon the values that some traits may take, that naturally arise from the ecological axiom that all viable populations require resources to grow (i.e. that $f_{i}|_{R_{i}= 1}>0>f_{i}|_{R_{i}= 0}$), suggest that some phenotypes have gamma distributions as they are constrained to be positive, negative, or greater or lesser than other parameters. Such constraints arise naturally in LVCN systems, and are fundamental to the system being ecologically valid. Here, where Eq. 1 represents competition between two populations, one incumbent and one potential invader, the parameter relations (2) are fundamental.

We follow the derivation of Lande (1976) and consider the evolution of phenotypes based on an equation provided by Falconer (1960) that describes the deterministic change in the average value of a phenotypic character $\bar {z}$ in response to selection:

$$\begin{array}{@{}rcl@{}} {\Delta} \bar{z}(t) &=&\bar{z}(t + 1)-\bar{z}(t), \\ &=& [ \bar{z}_{w}(t)-\bar{z}(t)]h^{2}, \end{array} $$

(10)

where $\bar {z}(t)$ is the mean value of the character in generation t before selection, $\bar {z}_{w}(t)$ is the mean value of the character after selection, but before reproduction, and h² is the realised heritability of the character. We denote the distribution of phenotypes z in the generation t before selection as p(z, t), and then the average phenotype before selection is:

$$ \bar{z}(t)=\int zp(z,t)dz, $$

(11)

the mean fitness of individuals in the population is:

$$ \bar{W}=\int p(z,t)W(z)dz, $$

(12)

and the average phenotype after selection is:

$$ \bar{z}_{w}(t)=\frac{1}{\bar{W}} \int z p(z,t) W(z) dz. $$

(13)

Then assuming that the phenotype has a γ-distribution:

$$\begin{array}{@{}rcl@{}} p(z,t) &=& \frac{\beta^{\alpha}}{{\Gamma}(\alpha)} z^{\alpha-1} e^{-\beta z}, \\ &=& \frac{\alpha^{\alpha} z^{\alpha-1}} {{\Gamma}(\alpha)} \bar{z}(t)^{-\alpha} e^{-\frac{\alpha z}{\bar{z}(t)}}, \end{array} $$

(14)

where we have used $\bar {z}(t)=\alpha / \beta$ to eliminate β. This gives the change in mean fitness of the population ($\bar {W}$) with respect to a change in the average phenotype ($\bar {z}(t)$) as:

$$\begin{array}{@{}rcl@{}} \frac{\partial \bar{W}}{\partial \bar{z}(t)} &=& \int \frac{\partial p(z,t)}{\partial \bar{z}(t)} W(z) dz, \\ &=& \int \frac{\alpha[z-\bar{z}(t)]}{\bar{z}(t)} p(z,t) W(z) dz, \\ &=& \frac{\alpha \bar{W}}{\bar{z}(t)^{2}} [\bar{z}_{w}(t)-\bar{z}(t)]. \end{array} $$

(15)

Then combining (15) with (10) gives:

$$\begin{array}{@{}rcl@{}} {\Delta} \bar{z}(t) &=& \frac{h^{2} \bar{z}(t)^{2}}{\alpha \bar{W}} \frac{\partial \bar{W}}{\partial \bar{z}(t)}, \\ &=& \frac{h^{2}\bar{z}(t)}{\beta} \frac{\partial \ln \bar{W}}{\partial \bar{z}(t)}. \end{array} $$

(16)

Note that $\bar {z}(t)/\beta$ is equivalent to the variance of the distribution, and represents the change in variance of the distribution as the mean approaches the lower bound (zero in the general case). As parameters in LVCN models may have lower bounds other than zero, for example a_ij in Eq. 1, we allow for a non-zero lower bound z_L in Eq. 16 and assume continuous trait variation:

$$ \frac{d \bar{z}}{dt} = h^{2} \left( \frac{\bar{z}(t)-z_{L}}{\beta} \right) \frac{\partial \ln \bar{W}}{\partial \bar{z}(t)}. $$

(17)

Equation 17 ensures that phenotypes with bounded distributions are not able to exceed their bounds during simulations.

The key attribute of traits that have gamma distributions for eco-evolutionary modelling is that the mean value of the trait is bounded and the variance is related to the mean trait value, so that as the mean of the trait approaches its bound the variance of the distribution of the trait reduces.