Skip to main content
SpringerLink
Log in

MRAC based intelligent PID controller design technique for a class of dynamical systems

  • Published:
Sādhanā Aims and scope Submit manuscript

Abstract

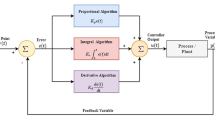
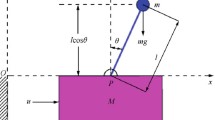
Model-Free Control (MFC) is used to control a complex system by designing a simple representation of the system, known as ultralocal model. This MFC continuously updates the input-output behavior with the help of ultralocal model. The combination of MFC with standard Proportional Integral Derivative (PID) controller develops Intelligent Proportional Integral Derivative (i-PID) controller. The i-PID controller is basically a class of robust control technique in the field of PID controller. In this methodology, the tuning is quite straightforward for extremely nonlinear and/or time varying plants, without consideration of any modeling procedure. In Model Reference Adaptive Controller (MRAC)-PID controller principle, PID parameters are updated/tuned in accordance with control technique based on MRAC-Massachusetts Institute of Technology (MIT) rule, such that the plant is efficient to follow the reference model. The main objective of this paper is to implement MRAC based Intelligent PID controller for a class of dynamical systems using Model-Free Control technique, where the prior knowledge about the system dynamic is not essential and moreover complex parameter tuning is not necessary.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Figure 1
Figure 2
Figure 3
Figure 4

Similar content being viewed by others

Abbreviations

i-P:

Intelligent Proportional

i-PD:

Intelligent Proportional Derivative

i-PI:

Intelligent Proportional Integral

i-PID:

Intelligent Proportional Integral Derivative

MFC:

Model-Free Control

MIT:

Massachusetts Institute of Technology

MRAC:

Model Reference Adaptive Controller

PID:

Proportional Integral Derivative

References

  1. Fliess M and Join C 2009 Model-free control and intelligent PID controllers: Towards a possible trivialization of nonlinear control. In: Proc.15th IFAC Symp. Syst. Identificat. (SYSID). 1531–1550

  2. Fliess M and Join C 2013 Model-free control. Int. J. Control. 1–25

  3. Fliess M and Join C 2021 An alternative to proportional-integral and proportional-integral-derivative regulators: Intelligent proportional-derivative regulators. Int. J. Robust Nonlinear Control. 1–13

  4. Fliess M and Join C 2008 Intelligent PID Controllers. Mediterranean Conference on Control and Automation. 326–331

  5. Fliess M and Join C 2009 Model-Free Control and Intelligent PID Controllers: towards a Possible Trivialization of Nonlinear Control. Proceedings of the 15th IFAC Symposium on System Identification. 1531-1550

  6. Åström K and Hägglund T 2001 The future of PID control. Control Eng. Pract. 9(11): 1163–1175.

    Article  Google Scholar 

  7. Astrom K, Hagglund T, Hang C C and Ho K W 1993 Automatic tuning and adaptation for PID controllers-A survey. Control Eng. Pract. 1(4): 699–714.

    Article  Google Scholar 

  8. Fliess M and Join C 2014 Stability margins and model-free control: A first look. European Control Conference. 454–459

  9. Doye N I, Asiri S, Aloufi A, Al-Awan A and Laleg-Kirati M T 2019 Intelligent proportional–integral–derivative control-based modulating functions for laser beam pointing and stabilization. IEEE Trans. Control Syst. Technol. 1–8

  10. Michel L, Join C, Fliess M, Sicard P and Chériti A 2010 Model-free control of DC/DC converters. IEEE 12th Workshop on Control and Modeling for Power Electronics (COMPEL). 1–8

  11. Miras D J, Join C, Fliess M, Riachy S and Bonnet S 2013 Active magnetic bearing: A new step for model-free control. In: Proc. IEEE Conf. Decision Control. 7449–7454

  12. Lafont F, Balmat F J, Pessel N and Fliess M 2015 A model-free control strategy for an experimental greenhouse with an application to fault accommodation. Comput. Electron. Agric. 110: 139–149.

    Article  Google Scholar 

  13. Menhour L, D’Andréa-Novel B, Fliess M and Mounier H 2013 Multivariable decoupled longitudinal and lateral vehicle control: A model free design. In Proc. IEEE Conf. Decision Control. 2834–2839

  14. Choi S, D’Andréa-Novel B, Fliess M, Mounier H and Villagra J 2009 Model-free control of automotive engine and brake for stop-and-go scenarios. In: Proc. Eur. Control Conf. 3622–3627

  15. Astrom J K and Wittenmark B 2001 Adaptive Control. Pearson Education Asia. 185–225

  16. Jain P and Nigam J M 2013 Design of a model reference adaptive controller using modified MIT rule for a second order system. Adv. Electron. Electric Eng. 3(4): 477–484.

    Google Scholar 

  17. Singh B and Kumar V 2015 A Real Time Application of Model Reference Adaptive PID Controller for Magnetic Levitation System IEEE Power, Communication and Information Technology Conference (PCITC).583–588

  18. Swathi M and Ramesh P 2017 Modeling and Analysis of Model Reference Adaptive Control by Using MIT and Modified MIT Rule for Speed Control of DC Motor. IEEE 7th International Advance Computing Conference. 482–486

  19. Swarnkar P, Jain K S and Nema K R 2011 Comparative analysis of MIT rule and lyapunov rule in model reference adaptive control scheme. Innov. Syst. Design Eng. 2(4): 154–162.

    Google Scholar 

  20. Pirabakaran K and Becerra M V 2001 Automatic tuning of PID Controllers using Model Reference Adaptive Control Techniques Proceedings of the 27th Annual Conference of the IEEE Industrial Electronics Society. 1: 736–740

  21. Xiong A and Fan Y 2007 Application of a PID Controller using MRAC Techniques for Control of the DC Electromotor Drive IEEE International Conference on Mechatronics and Automation.2616–2621

  22. Younes A Y, Drak A, Noura H, Rabhi A and Hajjaji E A 2016 Robust model-free control applied to a quadrotor UAV. J. Intell. Robotic Syst. 84: 37–52.

    Article  Google Scholar 

  23. Madonski R and Herman P 2013 Model-free control of a two dimensional system based on uncertainty reconstruction and attenuation. Conference on Control and Fault-Tolerant Systems (SysTol). 542–547

  24. Andary S, Chemori A, Benoit M and Sallantin J 2012 A Dual Model-Free Control of Underactuated Mechanical Systems, Application to The Inertia Wheel Inverted Pendulum. Proc. American Control Conference, 1029–1034

  25. Novel A D B, Fliess M, Join C, Mounier H and Steux B 2010 A mathematical explanation via "intelligent" PID controllers of the strange ubiquity of PIDs. 18th Mediterranean Conference on Control and Automation. 395–400

  26. Krishnaswamy K 2009 Process Control. New Age International Publishers, pp 14–15.

    Google Scholar 

  27. Nagrath I J and Gopal M 2009 Control Systems Engineering. New Age International Publishers, pp 52–57.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Applied Electronics and Instrumentation Engineering, Bankura Unnayani Institute of Engineering, Bankura, 722146, India

    Santanu Mallick

  2. Instrumentation Engineering, Department of Applied Physics, University of Calcutta, Kolkata, 700009, India

    Ujjwal Mondal

Authors
  1. Santanu Mallick
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ujjwal Mondal
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Santanu Mallick.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mallick, S., Mondal, U. MRAC based intelligent PID controller design technique for a class of dynamical systems. Sādhanā 49, 166 (2024). https://doi.org/10.1007/s12046-024-02457-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12046-024-02457-4

Keywords

Search

Navigation