Stability analysis of homogeneous unsaturated soil slopes by using the variational method

Abstract

The present study aims at addressing the stability of homogenous soil slopes by duly considering the unsaturated properties of the soil above the water table. The variational technique which is developed on the framework of the limit equilibrium method is employed to determine the critical factor of safety and the corresponding critical slip surfaces. The unsaturated soil above the water table is modelled by incorporating the suitable soil water characteristics curve and hydraulic conductivity function and on the basis of the suction-stress-based effective stress approach. An extensive parametric study is carried out to understand the combined effect of slope geometry, strength properties, hydromechanical parameters, location of the water table, and the impact of climatic conditions. The flows within the soil are considered unidirectional and are of three types, namely, evaporation (positive), precipitation (negative), and no-flow type (zero flow). Stability charts and slip surfaces are produced to show the effect of fluctuations in the water table and climatic conditions. The computed solutions match quite well with the existing solutions available in the literature.

Appendices

Appendix A

$$ {\text{GD}}\;{\text{SWCC}}\left[ {\displaystyle \frac{{\partial^{2} h_{m} }}{{\partial z^{2} }} + \alpha \left( {\displaystyle \frac{{\partial h_{m} }}{\partial z}} \right)^{2} } \right] + \alpha \displaystyle \frac{{\partial h_{m} }}{\partial z} = \displaystyle \frac{{\alpha \left( {\theta_{s} - \theta_{r} } \right)}}{{k_{s} }}\displaystyle \frac{{\partial h_{m} }}{\partial t} $$

(20)

$$ {\text{vG}}\;{\text{SWCC}}\left[ {\displaystyle \frac{1}{{\gamma_{w} }}\displaystyle \frac{{\partial^{2} h_{m} }}{{\partial z^{2} }} + \alpha \left( {\displaystyle \frac{{\partial h_{m} }}{\partial z}} \right)^{2} + \alpha \displaystyle \frac{{\partial h_{m} }}{\partial z}} \right] = - \displaystyle \frac{{mn\alpha \left( {\theta_{s} - \theta_{r} } \right)\left( {\alpha \gamma_{w} h_{m} } \right)^{n - 1} }}{{k_{s} \exp \left( {\alpha \gamma_{w} h_{m} } \right)\left\{ {1 + \left[ {\alpha \gamma_{w} h_{m} } \right]^{n} } \right\}^{m + 1} }}\frac{{\partial h_{m} }}{\partial t} $$

(21)

In terms of finite difference terms, the generalized equations for ith node can be written as:

$$ \left[ {\frac{{h_{m,i - 1}^{t + \Delta t} - 2h_{m,i}^{t + \Delta t} + h_{m,i + 1}^{t + \Delta t} }}{{\Delta z^{2} }} + \alpha \left[ {\frac{{h_{m,i + 1}^{t} - h_{m,i}^{t} }}{\Delta z}} \right]^{2} } \right] + \alpha \left[ {\frac{{h_{m,i + 1}^{t + \Delta t} - h_{m,i}^{t + \Delta t} }}{\Delta z}} \right] = \frac{1}{{L_{1} }}\frac{{h_{m,i}^{t + \Delta t} - h_{m,i}^{t} }}{\Delta t} $$

(22a)

$$ \Rightarrow - m_{1} h_{m,i - 1}^{t + \Delta t} + \left( {1 + 2m_{1} + m_{3} } \right)h_{m,i}^{t + \Delta t} - \left( {m_{1} + m_{3} } \right)h_{m,i + 1}^{t + \Delta t} = h_{m,i}^{t} + m_{2} \left( {h_{m,i + 1}^{t} - h_{m,i}^{t} } \right)^{2} $$

(22b)

$$ \begin{gathered} m_{1} = \frac{{L_{1} \Delta t}}{{\Delta z^{2} }},m_{2} = \frac{{L_{1} \alpha \Delta t}}{{\Delta z^{2} }},m_{3} = \frac{{L_{1} \alpha \Delta t}}{\Delta z};L_{1}^{GD} = \frac{{k_{s} }}{{\alpha \left( {\theta_{s} - \theta_{r} } \right)}};L_{1}^{vG} = \frac{{ - k_{s} e^{{\alpha \gamma_{w} h_{m,i}^{t} }} \left\{ {1 + \left[ {\alpha \gamma_{w} h_{m,i}^{t} } \right]^{n} } \right\}^{m + 1} }}{{mn\alpha^{n} \left( {\theta_{s} - \theta_{r} } \right)\left( {\gamma_{w} h_{m,i}^{t} } \right)^{n - 1} }} \hfill \\ h_{m,n + 2}^{t + \Delta t} = h_{m,n}^{t + \Delta t} + 2\Delta zQ\exp \left( { - \alpha \gamma_{w} h_{m,n + 1}^{t} } \right) - 2\Delta z \hfill \\ \end{gathered} $$

(22c)

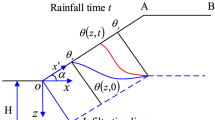
Here,$h_{m,i + 1}^{t} ,h_{m,i}^{t}$, and $h_{m,i - 1}^{t}$ are the matric suction head at node i+1, i, and i−1 (as shown in Figure 2) at time t.

The simultaneous set of linear equation can be rewritten as:

$$ {\varvec{AH}}_{m}^{t + \Delta t} = {\varvec{B}} $$

(23)

$$ A = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ { - m_{1} } & {\left( {1 + 2m_{1} + m_{3} } \right)} & { - \left( {m_{1} + m_{3} } \right)} & 0 & 0 & 0 & 0 \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0 & 0 & { - m_{1} } & {\left( {1 + 2m_{1} + m_{3} } \right)} & { - \left( {m_{1} + m_{3} } \right)} & \cdots & 0 \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0 & 0 & 0 & 0 & { - m_{1} } & {\left( {1 + 2m_{1} + m_{3} } \right)} & { - \left( {m_{1} + m_{3} } \right)} \\ 0 & 0 & 0 & 0 & 0 & { - \left( {2m_{1} + m_{3} } \right)} & {\left( {1 + 2m_{1} + m_{3} } \right)} \\ \end{array} } \right]_{{\left( \begin{subarray}{l} n + 1 \\ \times n + 1 \end{subarray} \right)}} $$

$$ {\varvec{H}}_{m}^{t + \Delta t} = \left[ {\begin{array}{*{20}c} {h_{m,1}^{t + \Delta t} } & {h_{m,2}^{t + \Delta t} } & \ldots & \ldots & {h_{m,i - 1}^{t + \Delta t} } & {h_{m,i}^{t + \Delta t} } & {h_{m,i + 1}^{t + \Delta t} } & \ldots & \ldots & {\begin{array}{*{20}c} {h_{m,n}^{t + \Delta t} } & {h_{m,n + 1}^{t + \Delta t} } \\ \end{array} } \\ \end{array} } \right]_{1 \times (n + 1)}^{T} $$

$$ {\varvec{B}}^{{\varvec{t}}} = \left[ {\begin{array}{*{20}c} {B_{1} } & {B_{2} } & \ldots & \ldots & {B_{i - 1} } & {B_{i} } & {B_{i + 1} } & \ldots & \ldots & {B_{n} } & {B_{n + 1} } \\ \end{array} } \right]_{1 \times (n + 1)}^{T} $$

$$ B_{1} = 0;B_{i} = h_{m,i}^{t} + m_{2} \left( {h_{m,i + 1}^{t} - h_{m,i}^{t} } \right)^{2} ;B_{n} = h_{m,n}^{t} + m_{2} \left( {h_{m,n + 1}^{t} - h_{m,n}^{t} } \right)^{2} $$

Equation (23) is further solved by employing Gauss Elimination scheme.

Appendix B

(i) Two transversality conditions (applied at x₀ and x_n):

$$ [Q_{{y^{\prime } }} - F_{s} R_{{y^{\prime } }} ][f^{\prime } (x) - y^{\prime } (x)] + P - F_{s} R|_{{x = x_{0} }} = 0 \, $$

(24a)

$$ [Q_{{y^{\prime } }} - F_{s} R_{{y^{\prime } }} ][f^{\prime } (x) - y^{\prime } (x)] + P - F_{s} R|_{{x = x_{n} }} = 0 \, $$

(24b)

(ii) Two boundary conditions (applied at x₀ and x_n):

$$ y_{1} \left( {x_{0} } \right) = f_{1} (x_{0} ) $$

(25a)

$$ y_{n} \left( {x_{n} } \right) = f_{3} \left( {x_{n} } \right) $$

(25b)

(iii) (n−1) zeroth order continuity conditions applied at intermediate points:

$$ y_{i} (x_{i} ) = y_{i + 1} (x_{i} )\quad (i = 1,2,3,4, \ldots ,n - 1) $$

(26)

(iv) (n -1) first order continuity conditions applied at intermediate points:

$$ y_{i}^{\prime } (x_{i} ) = y_{i + 1}^{\prime } (x_{i} )\quad (i = 1,2,3,4, \ldots ,n - 1) $$

(27)

(v) The equation for Factor of Safety expressed as:

$$ F = \frac{{\int\limits_{{x_{0} }}^{{x_{1} }} {Q_{1} \left( {x,y,y^{\prime } } \right)dx + \int\limits_{{x_{1} }}^{{x_{2} }} {Q_{2} (x,y,y^{\prime } )dx + \int\limits_{{x_{2} }}^{{x_{3} }} {Q_{3} (x,y,y^{\prime } )dx} } } }}{{\int\limits_{{x_{0} }}^{{x_{1} }} {R_{1} \left( {x,y,y^{\prime } } \right)dx + \int\limits_{{x_{1} }}^{{x_{2} }} {R_{2} (x,y,y^{\prime } )dx + \int\limits_{{x_{2} }}^{{x_{3} }} {R_{3} (x,y,y^{\prime } )dx} } } }} $$

(28)