Skip to main content
SpringerLink
Log in

Optimization based synthesis of pelvic structure for loads in running gait cycle

  • Published:
Sādhanā Aims and scope Submit manuscript

Abstract

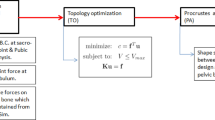
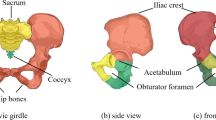
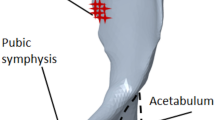
Pelvic bone is a complex and robust load-bearing skeletal structure in the human body, the evolution of which might have been influenced by mechanical loads of daily activities like walking, upright standing, and running. Since the main function of skeletal bones is to provide rigidity to the body and provide hard surfaces for muscle attachment as well, in this work we propose a compliance minimization problem to determine whether material distribution guided by topology optimization yields a skeletal structure similar to the pelvic bone under same boundary conditions and volumetric constraints. As bone growth occurs in response to the mechanical loads acting on it, we consider the maximal loads that the pelvic bone may experience for a continued period of time, namely during running. The running gait cycle is divided into seven phases, and the objective function is a weighted combination of these seven phases. The optimal geometries are compared with the natural hemi-pelvis by measuring shape similarity using Procrustes analysis. Results show that the optimal geometries have good shape similarity in stance phases. We also explore the design space by considering a combination of sequence of phases which is an alternative to the weighted multiple load-case objective function. In all cases, the optimal geometries are stiffer than the hip bone. To validate this result, we conducted compression test experiments on selected optimal geometries and natural hemi-pelvis model of same material and found that the experimental results prove that topology optimization based optimal geometries are indeed more stiff than the natural hemi-pelvis geometry.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Figure 1
Figure 2
Figure 3
Figure 4
Figure 5
Figure 6
Figure 7
Figure 8
Figure 9
Figure 10
Figure 11

Similar content being viewed by others

References

  1. Mellon S J and Tanner K E 2012 Bone and its adaptation to mechanical loading: A review. Int. Mater. Rev. 57(5): 235–255

    Article  Google Scholar 

  2. Turner C H 1998 Three rules for bone adaptation to mechanical stimuli. Bone 23(5): 399–407

    Article  Google Scholar 

  3. Wolff J 1892 The Law of Bone Remodelling. Translated version, 1986, Springer

  4. Cowin S C, Moss-Salentijn L and Moss M L 1991 Candidates for the mechanosensory system in bone. J. Biomech. Eng. 113(2): 191–197

    Article  Google Scholar 

  5. Weinans H, Huiskes R and Grootenboer H J 1992 The behavior of adaptive bone-remodeling simulation models. J. Biomech. 25(12): 1425–1441

    Article  Google Scholar 

  6. Harrigan T P and Hamilton J J 1993 Finite element simulation of adaptive bone remodelling: A stability criterion and a time stepping method. Int. J. Numer. Methods Eng. 36(5): 837–854

    Article  Google Scholar 

  7. Fyhrie D and Schaffler M B 1995 The adaptation of bone apparant density to applied load. J. Biomech. 28(2): 135–146

    Article  Google Scholar 

  8. Levenston M E and Carter D R 1998 An energy dissipation-based model for damage stimulated bone adaptation. J. Biomech. 31(7): 579–586

    Article  Google Scholar 

  9. Ruimerman R, Hilbers P, Van Rietbergen B and Huiskes R 2005 A theoretical framework for strain-related trabecular bone maintenance and adaptation. J. Biomech. 38(4): 931–941

    Article  Google Scholar 

  10. Hollister S J, Kikuchi N and Goldstein S A 1993 Do bone ingrowth processes produce a globally optimized structure? J. Biomech. 26(4–5): 391–407

    Article  Google Scholar 

  11. Fernandes P, Rodrigues H and Jacobs C 1999 A model of bone adaptation using a global optimisation criterion based on the trajectorial theory of Wolff. Comput. Methods Biomech. Biomed. Eng. 2(2): 125–138

    Article  Google Scholar 

  12. Bagge M 2000 A model of bone adaptation as an optimization process. J. Biomech. 33(11): 1349–1357

    Article  Google Scholar 

  13. Fernandes P R, Folgado J, Jacobs C and Pellegrini V 2002 A contact model with ingrowth control for bone remodelling around cementless stems. J. Biomech. 35(2): 167–176

    Article  Google Scholar 

  14. Nowak M 2006 Structural optimization system based on trabecular bone surface adaptation. Struct. Multidiscipl. Optim. 32(3): 241–249

    Article  Google Scholar 

  15. Sutradhar A, Paulino G H, Miller M J and Nguyen T H 2010 Topological optimization for designing patient-specific large craniofacial segmental bone replacements. PNAS 107(30): 13222–13227

    Article  Google Scholar 

  16. Lekszycki T 1999 Optimality conditions in modeling of bone adaptation phenomenon. J. Theor. Appl. Mech. 37(3): 607–624

    MATH  Google Scholar 

  17. Lekszycki T 2002 Modelling of bone adaptation based on an optimal response hypothesis. Meccanica 37(4–5): 343–354

    Article  MathSciNet  MATH  Google Scholar 

  18. Rodrigues H, Jacobs C, Guedes J M and Bendsoe M P 2002 Global and local material optimization models applied to anisotropic bone adaptation. In: Pedersen P, Bendsoe MP (eds) IUTAM Symposium on Synthesis in Bio Solid Mechanics, Springer, Dordrecht, pp. 209–220

    Chapter  Google Scholar 

  19. Goel V K and Svensson N L 1977 Forces on the pelvis. J. Biomech. 10(3): 195–200

    Article  Google Scholar 

  20. Dostal W F and Andrews J G 1981 A three dimensional Biomechanical model of Hip Musculature. J. Biomech. 14(11): 803–812

    Article  Google Scholar 

  21. Dalstra M, Huiskes R and van Erning L 1995 Development and validation of a three-dimensional finite element model of the pelvic bone. J. Biomech. Eng. 117(3): 272–278

    Article  Google Scholar 

  22. Ghosh R, Pal B, Ghosh D and Gupta S 2015 Finite element analysis of a hemi-pelvis: the effect of inclusion of cartilage layer on acetabular stresses and strain. Comput. Methods Biomech. Biomed. Eng. 18(7): 697–710

    Article  Google Scholar 

  23. Ricci P L, Maas S, Kelm J and Gerich T 2018 Finite element analysis of the pelvis including gait muscle forces: an investigation into the effect of rami fractures on load transmission. J. Exp. Orthop. 5(1): 1–9

    Article  Google Scholar 

  24. Goel V K, Valliappan S and Svensson N L 1978 Stresses in the normal pelvis. Comput. Biol. Med. 8(2): 91–104

    Article  Google Scholar 

  25. Hu P, Wu T, Wang H Z, Qi X Z, Yao J, Cheng X D, Chen W and Zhang Y Z 2017 Influence of different boundary conditions in finite element analysis on pelvic biomechanical load transmission. J. Orthop. Surg. 9(1): 115–122

    Article  Google Scholar 

  26. Kumar K E S and Rakshit S 2020a Topology optimization of the hip bone for gait cycle. Struct. Multidiscipl. Optim. 62(4): 2035–2049

    Article  MathSciNet  Google Scholar 

  27. Sutradhar A, Park J, Carrau D, Nguyen T H, Miller M J and Paulino G H 2016 Designing patient-specific 3D printed craniofacial implants using a novel topology optimization method. Med. Biol. Eng. Comput. 54(7): 1123–1135

    Article  Google Scholar 

  28. Mei J, Ni M, Gao Y S and Wang Z Y 2014 Femur performed better than tibia in autologous transplantation during hemipelvis reconstruction. World J. Surg. Oncol. 12(1): 2–7

    Article  Google Scholar 

  29. Wang B, Xie X, Yin J, Zou C, Wang J, Huang G, Wang Y and Shen J 2015 Reconstruction with modular hemipelvic endoprosthesis after pelvic tumor resection: A report of 50 consecutive cases. PLoS ONE 10(5): 1–11

    Google Scholar 

  30. Simonsen E B, Thomsen L and Klausen K 1985 Activity of mono- and biarticular leg muscles during sprint running. Eur. J. Appl. Physiol. 54(5): 524–532

    Article  Google Scholar 

  31. Nilsson J and Thorstensson A 1989 Ground reaction forces at different speeds of human walking and running. Acta Physiol. Scand. 136: 217–227

    Article  Google Scholar 

  32. Schache A G, Blanch P, Rath D, Wrigley T and Bennell K 2002 Three-dimensional angular kinematics of the lumbar spine and pelvis during running. Hum. Mov. Sci. 21: 273–293

    Article  Google Scholar 

  33. Bendsoe M P and Sigmund O 2004 Topology Optimization: Theory, Methods and Applications, 2nd ed. Springer

  34. Sigmund O 2001 A 99 line topology optimization code written in matlab. Struct. Multidiscipl. Optim. 21: 120–127

    Article  Google Scholar 

  35. Park J, Lee D and Sutradhar A 2019 Topology optimization of fixed complete denture framework. Int. J. Numer. Methods Biomed. Eng. 35(6): 1–11

    Article  Google Scholar 

  36. TheMotionMechanic 2019 Wordpress. http://www.themotionmechanic.com/2019/02/20/thebiomechanics-of-running-3-common-technique-faults/

  37. Hamner S R, Seth A and Delp S L 2010 Muscle contributions to propulsion and support during running. J. Biomech. 43(14): 2709–2716

    Article  Google Scholar 

  38. Phillips A T, Villette C C and Modenese L 2015 Femoral bone mesoscale structural architecture prediction using musculoskeletal and finite element modelling. Int. Biomech. 2(1): 43–61

    Article  Google Scholar 

  39. Van Arkel R J, Modenese L, Phillips A T and Jeffers J R 2013 Hip abduction can prevent posterior edge loading of hip replacements. J. Orthop. Res. 31(8): 1172–1179

    Article  Google Scholar 

  40. Cavanagh P R and Lafortune M A 1980 Ground reaction forces in distance running. J. Biomech. 13: 397–406

    Article  Google Scholar 

  41. Novacheck T F 1998 The biomechanics of running. Gait Posture 7(1): 77–95

    Article  Google Scholar 

  42. Geraldes D M, Modenese L and Phillips A T 2016 Consideration of multiple load cases is critical in modelling orthotropic bone adaptation in the femur. Biomech. Model. Mechanobiol. 15(5): 1029–1042

    Article  Google Scholar 

  43. Bendsoe M P and Sigmund O 1999 Material interpolation schemes in topology optimization. Arch. Appl. Mech. 69(9): 635–654

    MATH  Google Scholar 

  44. Uri K 1994 Efficient sensitivity analysis for structural optimization. Comput. Methods Appl. Mech. Eng. 117: 143–156

    Article  MATH  Google Scholar 

  45. Sigmund O and Petersson J 1998 Numerical instabilities in topology optimization: A survey on procedures dealing with checkerboards, mesh-dependencies and local minima. Struct. Multidiscipl. Optim. 16: 68–75

    Article  Google Scholar 

  46. Bourdin B 2001 Filters in topology optimization. Int. J. Numer. Methods Eng. 50(9): 2143–2158

    Article  MathSciNet  MATH  Google Scholar 

  47. Anderson A E, Peters C L, Tuttle B D, Weiss J A 2005 Subject-specific finite element model of the pelvis: development, validation and sensitivity studies. J. Biomech. Eng. 127(3): 364–373

    Article  Google Scholar 

  48. Kumar K E S and Rakshit S 2021 Topology optimization of the hip bone for a few activities of daily living. Int. J. Adv. Eng. Sci. Appl. Math. 12(3): 193–210

    MathSciNet  Google Scholar 

  49. Kumar K E S and Rakshit S 2020b Topology Optimization of the Pelvic Bone Prosthesis Under Single Leg Stance. In: Volume 11B: ASME-IDETC&CIE, v11BT11A030

  50. Kumar K E S and Rakshit S 2021 Design of pelvic prosthesis using topology optimization for loads in running gait cycle. J. Inst. Eng. (India) C 102(96): 1119–1128

    Article  Google Scholar 

  51. Zhao X, Liu Y, Hua L and Mao H 2016 Finite element analysis and topology optimization of a 12000KN fine blanking press frame. Struct. Multidiscipl. Optim. 54(2): 375–389

    Article  Google Scholar 

  52. Gower J C 1975 Generalized procrustes analysis. Psychometrika 40(1): 33–51

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors thank Prof. C. Sujatha, Department of Mechanical Engineering, IIT Madras, for providing the geometric model of the pelvic bone. Prof. Ratna Kumar Annabattula, Department of Mechanical Engineering, IIT Madras, is gratefully acknowledged for allowing us to conduct experiments on the UTM in Mechanics of Materials lab in Machine Design Section, IIT Madras.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Indian Institute of Science, Bengaluru, India

    Kandula Eswara Sai Kumar

  2. Department of Mechanical Engineering, Indian Institute of Technology, Madras, India

    Sourav Rakshit

Authors
  1. Kandula Eswara Sai Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sourav Rakshit
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sourav Rakshit.

Ethics declarations

Conflict of interest

The authors declare that they have no conflicts of interest.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kumar, K.E.S., Rakshit, S. Optimization based synthesis of pelvic structure for loads in running gait cycle. Sādhanā 47, 118 (2022). https://doi.org/10.1007/s12046-022-01881-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12046-022-01881-8

Keywords

Search

Navigation