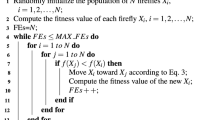Skip to main content
SpringerLink
Log in

A partition cum unification based genetic- firefly algorithm for single objective optimization

  • Published:
Sādhanā Aims and scope Submit manuscript

Abstract

Firefly algorithm is one of the most promising population-based meta-heuristic algorithms. It has been successfully applied in many optimization problems. Several modifications have been proposed to the original algorithm to boost the performance in terms of accuracy and speed of convergence. This work proposes a partition cum unification based genetic firefly algorithm to explore the benefits of both the algorithms in a novel way. With this, the initial population is partitioned into two compartments based on a weight factor. An improved firefly algorithm runs in the first compartment, whereas, the genetic operators like selection, crossover, and mutation are applied on the relatively inferior fireflies in the second compartment giving added exploration abilities to the weaker solutions. Finally, unification is applied on the subsets of fireflies of the two compartments before going to the next iterative cycle. The new algorithm in three variants of weightage factor have been compared with the two constituents i.e. standard firefly algorithm and genetic algorithm, additionally with some state-of-the-art meta-heuristics namely particle swarm optimization, cuckoo search, flower pollination algorithm, pathfinder algorithm and bio-geography based optimization on 19 benchmark objective functions covering different dimensionality of the problems viz. 2-D, 16-D, and 32-D. The new algorithm is also tested on two classical engineering optimization problems namely tension-compression spring and three bar truss problem and the results are compared with all the other algorithms. Non-parametric statistical tests, namely Wilcoxon rank-sum tests are conducted to check any significant deviations in the repeated independent trials with each algorithm. Multi criteria decision making tool is applied to statistically determine the best performing algorithm given the different test scenarios. The results show that the new algorithm produces the best objective function value for almost all the functions including the engineering problems and it is way much faster than the standard firefly algorithm.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Figure 1
Figure 2
Figure 3
Figure 4
Figure 5
Figure 6
Figure 7
Figure 8
Figure 9
Figure 10
Figure 11
Figure 12
Figure 13
Figure 14
Figure 15
Figure 16
Figure 17
Figure 18
Figure 19
Figure 20
Figure 21
Figure 22
Figure 23
Figure 24
Figure 25
Figure 26
Figure 27
Figure 28
Figure 29
Figure 30
Figure 31
Figure 32
Figure 33
Figure 34

Similar content being viewed by others

References

  1. Xin-She Yang. Nature-inspired metaheuristic algorithms. Luniver press, 2010

  2. Ilhem Boussaïd, Julien Lepagnot, and Patrick Siarry. A survey on optimization metaheuristics. Information sciences, 237:82, 2013

    Article  MathSciNet  Google Scholar 

  3. John H Holland. Genetic algorithms and adaptation. In Adaptive Control of Ill-Defined Systems, pp 317. Springer, 1984

  4. Kalyanmoy Deb. An introduction to genetic algorithms. Sādhanā, 24(4-5):293, 1999

    Article  MathSciNet  Google Scholar 

  5. Tansel Dokeroglu, Ender Sevinc, Tayfun Kucukyilmaz, and Ahmet Cosar. A survey on new generation metaheuristic algorithms. Computers & Industrial Engineering, 137:106040, 2019

    Article  Google Scholar 

  6. Kashif Hussain, Mohd Najib Mohd Salleh, Shi Cheng, and Yuhui Shi. Metaheuristic research: a comprehensive survey. Artificial Intelligence Review, 52(4):2191, 2019

    Article  Google Scholar 

  7. Xin-She Yang. Firefly algorithms for multimodal optimization. In International symposium on stochastic algorithms, p 169. Springer, 2009

  8. Waqar A Khan, Nawaf N Hamadneh, Surafel L Tilahun, and Ngnotchouye J M. A review and comparative study of firefly algorithm and its modified versions. Optimization Algorithms-Methods and Applications, p 281, 2016

  9. Iztok Fister, Iztok Fister Jr, Xin-She Yang, and Janez Brest 2013. A comprehensive review of firefly algorithms. Swarm and Evolutionary Computation, 13:34, 2013

  10. Nilanjan Dey. Applications of firefly algorithm and its variants. Springer, Berlin, 2020

    Book  Google Scholar 

  11. Mahmood Reza Shakarami and Reza Sedaghati. A new approach for network reconfiguration problem in order to deviation bus voltage minimization with regard to probabilistic load model and dgs. Int. J. Electr. Comput. Energ. Electr. Commun. Eng., 8(2):430, 2014

  12. Abdollah Kavousi-Fard, Haidar Samet, and Fatemeh Marzbani. A new hybrid modified firefly algorithm and support vector regression model for accurate short term load forecasting. Expert systems with applications, 41(13):6047, 2014

    Article  Google Scholar 

  13. Xiaoyu Lin, Yiwen Zhong, and Hui Zhang. An enhanced firefly algorithm for function optimisation problems. International Journal of Modelling, Identification and Control, 18(2):166, 2013

    Article  Google Scholar 

  14. Amir Hossein Gandomi, X-S Yang, S Talatahari, and Amir Hossein Alavi. Firefly algorithm with chaos. Communications in Nonlinear Science and Numerical Simulation, 18(1):89, 2013

  15. Mohd Herwan Sulaiman, Hamdan Daniyal, and Mohd Wazir Mustafa. Modified firefly algorithm in solving economic dispatch problems with practical constraints. In 2012 IEEE International Conference on Power and Energy (PECon), pp 157. IEEE, 2012

  16. Bin Wang, Dong-Xu Li, Jian-Ping Jiang, and Yi-Huan Liao. A modified firefly algorithm based on light intensity difference. Journal of Combinatorial Optimization, 31(3):1045, 2016

    Article  MathSciNet  Google Scholar 

  17. Shuhao Yu, Shoubao Su, Qingping Lu, and Li Huang. A novel wise step strategy for firefly algorithm. International Journal of Computer Mathematics, 91(12):2507, 2014

    Article  MathSciNet  Google Scholar 

  18. Amit Kumar Ball, Shibendu Shekhar Roy, Dakshina Ranjan Kisku, Naresh Chandra Murmu, and Leandro dos Santos Coelho. Optimization of drop ejection frequency in ehd inkjet printing system using an improved firefly algorithm. Applied Soft Computing, 94:106438, 2020

  19. Abhishek Ghosh Roy, Pratyusha Rakshit, Amit Konar, Samar Bhattacharya, Eunjin Kim, and Atulya K Nagar. Adaptive firefly algorithm for nonholonomic motion planning of car-like system. In 2013 IEEE Congress on Evolutionary Computation, pp 2162. IEEE, 2013

  20. Shuhao Yu, Shenglong Zhu, Yan Ma, and Demei Mao. Enhancing firefly algorithm using generalized opposition- based learning. Computing, 97(7):741, 2015

    Article  MathSciNet  Google Scholar 

  21. MJ Kazemzadeh-Parsi. A modified firefly algorithm for engineering design optimization problems. Iranian Journal of Science and Technology. Transactions of Mechanical Engineering, 38(M2):403, 2014

  22. Mohammad Javad Kazemzadeh-Parsi, Farhang Daneshmand, Mohammad Amin Ahmadfard, and Jan Adamowski. Optimal remediation design of unconfined contaminated aquifers based on the finite element method and a modified firefly algorithm. Water Resources Management, 29(8):2895, 2015

  23. Sirus Mohammadi, Babak Mozafari, Soodabeh Solimani, and Taher Niknam. An adaptive modified firefly optimisation algorithm based on hong’s point estimate method to optimal operation management in a microgrid with consideration of uncertainties. Energy, 51:339, 2013

    Article  Google Scholar 

  24. Tahereh Hassanzadeh and Hamidreza Rashidy Kanan. Fuzzy fa: a modified firefly algorithm. Applied Artificial Intelligence, 28(1):47, 2014

  25. Sankalap Arora, Sarbjeet Singh, Satvir Singh, and Bhanu Sharma. Mutated firefly algorithm. In 2014 International Conference on Parallel, Distributed and Grid Computing, p 33. IEEE, 2014

  26. Sankalap Arora and Satvir Singh. Performance research on firefly optimization algorithm with mutation. In International conference, computing & systems, 2014

  27. Wen-chuan Wang, Lei Xu, Kwok-wing Chau, and Dong-mei Xu. Yin-yang firefly algorithm based on dimensionally cauchy mutation. Expert Systems with Applications, 150:113216, 2020

    Article  Google Scholar 

  28. Hu Peng, Wenhua Zhu, Changshou Deng, and Zhijian Wu. Enhancing firefly algorithm with courtship learning. Information Sciences, 543:18, 2021

    Article  MathSciNet  Google Scholar 

  29. Nan Tong, Qiang Fu, Caiming Zhong, and Pengjun Wang. A multi-group firefly algorithm for numerical optimization. In Journal of Physics: Conference Series, vol 887, p 012060. IOP Publishing, 2017

  30. Lingyun Zhou, Lixin Ding, Maode Ma, and Wan Tang. An accurate partially attracted firefly algorithm. Computing, 101(5):477, 2019

    Article  MathSciNet  Google Scholar 

  31. Adil Baykasoğlu and Fehmi Burcin Ozsoydan. An improved firefly algorithm for solving dynamic multidimensional knapsack problems. Expert Systems with Applications, 41(8):3712, 2014

  32. Jingsen Liu, Yinan Mao, Xiaozhen Liu, and Yu Li. A dynamic adaptive firefly algorithm with globally orientation. Mathematics and Computers in Simulation, 2020

  33. Iztok Fister, Xin-She Yang, Janez Brest, and Iztok Fister Jr. Modified firefly algorithm using quaternion representation. Expert Systems with Applications, 40(18):7220, 2013

  34. Hui Wang, Wenjun Wang, Xinyu Zhou, Hui Sun, Jia Zhao, Xiang Yu, and Zhihua Cui. Firefly algorithm with neighborhood attraction. Information Sciences, 382:374, 2017

    Article  Google Scholar 

  35. Sh M Farahani, AA Abshouri, B Nasiri, and MR2011 Meybodi. A gaussian firefly algorithm. International Journal of Machine Learning and Computing, 1(5):448, 2011

  36. Xin-She Yang. Firefly algorithm, levy flights and global optimization. In Research and development in intelligent systems XXVI, p 209. Springer, 2010

  37. Lyes Tighzert, Cyril Fonlupt, and Boubekeur Mendil. A set of new compact firefly algorithms. Swarm and Evolutionary Computation, 40:92, 2018

    Article  Google Scholar 

  38. Jinran Wu, You-Gan Wang, Kevin Burrage, Yu-Chu Tian, Brodie Lawson, and Zhe Ding. An improved firefly algorithm for global continuous optimization problems. Expert Systems with Applications, 149:113340, 2020

    Article  Google Scholar 

  39. Jitin Luthra and Saibal K Pal. A hybrid firefly algorithm using genetic operators for the cryptanalysis of a monoalphabetic substitution cipher. In 2011 World congress on information and communication technologies, p 202. IEEE, 2011

  40. A Rahmani and SA MirHassani. A hybrid firefly-genetic algorithm for the capacitated facility location problem. Information Sciences, 283:70, 2014

    Article  MathSciNet  Google Scholar 

  41. Shubhendu Kumar Sarangi, Rutuparna Panda, Sabnam Priyadarshini, and Archana Sarangi. A new modified firefly algorithm for function optimization. In 2016 International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT), p 2944. IEEE, 2016

  42. İbrahim Berkan Aydilek, İzzettin Hakan Karaçizmeli, Mehmet Emin Tenekeci, Serkan Kaya, and Abdülkadir Gümüşçü. Using chaos enhanced hybrid firefly particle swarm optimization algorithm for solving continuous optimization problems. Sādhanā, 46(2):1, 2021

  43. Aref Yelghi and Cemal Köse. A modified firefly algorithm for global minimum optimization. Applied Soft Computing, 62:29, 2018

    Article  Google Scholar 

  44. Kadavy Tomas, Pluhacek Michal, Viktorin Adam, and Senkerik Roman. Firefly algorithm enhanced by orthogonal learning. In Computer Science On-line Conference, p 477. Springer, 2018

  45. Yu-Pei Huang, Xiang Chen, and Cheng-En Ye. A hybrid maximum power point tracking approach for photovoltaic systems under partial shading conditions using a modified genetic algorithm and the firefly algorithm. International Journal of Photoenergy, 2018, 2018

  46. Russell Eberhart and James Kennedy. Particle swarm optimization. In Proceedings of the IEEE international conference on neural networks, volume 4, pages 1942–1948. Citeseer, 1995

  47. Xin-She Yang and Suash Deb. Cuckoo search via lévy flights. In 2009 World congress on nature & biologically inspired computing (NaBIC), p 210. IEEE, 2009

  48. R Indumathy, S Uma Maheswari, and G Subashini. Nature-inspired novel cuckoo search algorithm for genome sequence assembly. Sādhanā, 40(1):1, 2015

  49. Xin-She Yang. Flower pollination algorithm for global optimization. In International conference on unconventional computing and natural computation, p 240. Springer, 2012

  50. Hamza Yapici and Nurettin Cetinkaya. A new meta-heuristic optimizer: pathfinder algorithm. Applied soft computing, 78:545, 2019

    Article  Google Scholar 

  51. Dan Simon. Biogeography-based optimization. IEEE transactions on evolutionary computation, 12(6):702, 2008

    Article  Google Scholar 

  52. Singiresu S Rao. Engineering optimization: theory and practice. John Wiley & Sons, 2019

  53. Amir Parnianifard, Ratchatin Chancharoen, Gridsada Phanomchoeng, and Lunchakorn Wuttisittikulkij. A new approach for low-dimensional constrained engineering design optimization using design and analysis of simulation experiments. International Journal of Computational Intelligence Systems, 13(1):1663, 2020

    Article  Google Scholar 

  54. Jasbir Singh Arora. Introduction to optimum design. Elsevier, 2004

  55. Young-Jou Lai, Ting-Yun Liu, and Ching-Lai Hwang. Topsis for modm. European journal of operational research, 76(3):486, 1994

    Article  Google Scholar 

  56. Momin Jamil and Xin-She Yang. A literature survey of benchmark functions for global optimization problems. arXiv preprintarXiv:1308.4008, 2013

  57. Sudhanshu K Mishra. Some new test functions for global optimization and performance of repulsive particle swarm method. Available at SSRN 926132, 2006

  58. Carlos A Coello Coello. Use of a self-adaptive penalty approach for engineering optimization problems. Computers in Industry, 41(2):113, 2000

  59. Joaquín Derrac, Salvador García, Daniel Molina, and Francisco Herrera. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm and Evolutionary Computation, 1(1):3, 2011

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, National Institute of Technology Durgapur, West Bengal, India

    Dhrubajyoti Gupta, Ananda Rabi Dhar & Shibendu Shekhar Roy

Authors
  1. Dhrubajyoti Gupta
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ananda Rabi Dhar
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Shibendu Shekhar Roy
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shibendu Shekhar Roy.

Supplementary Information

Below is the link to the electronic supplementary material.

Supplementary material 1 (jpg 1624 KB)

Supplementary material 2 (jpg 1581 KB)

Supplementary material 3 (jpg 1649 KB)

Supplementary material 4 (jpg 1587 KB)

Supplementary material 5 (jpg 1525 KB)

Supplementary material 6 (jpg 1646 KB)

Supplementary material 7 (jpg 1618 KB)

Supplementary material 8 (jpg 1552 KB)

Supplementary material 9 (jpg 1606 KB)

Supplementary material 10 (jpg 1493 KB)

Supplementary material 11 (jpg 1285 KB)

Supplementary material 12 (jpg 1408 KB)

Supplementary material 13 (jpg 1284 KB)

Supplementary material 14 (jpg 1245 KB)

Supplementary material 15 (jpg 1280 KB)

Supplementary material 16 (jpg 1363 KB)

Supplementary material 17 (jpg 1342 KB)

Supplementary material 18 (jpg 1409 KB)

Supplementary material 19 (jpg 1269 KB)

Supplementary material 20 (jpg 1330 KB)

Supplementary material 21 (jpg 1432 KB)

Supplementary material 22 (jpg 1382 KB)

Supplementary material 23 (jpg 1356 KB)

Supplementary material 24 (jpg 1350 KB)

Supplementary material 25 (jpg 1487 KB)

Supplementary material 26 (jpg 1445 KB)

Supplementary material 27 (jpg 1359 KB)

Supplementary material 28 (jpg 1220 KB)

Supplementary material 29 (jpg 1690 KB)

Supplementary material 30 (jpg 1624 KB)

Abbreviations

Abbreviations

GA:

Genetic algorithm

FA:

Firefly algorithm

PUBG-FA:

Partition cum unification based genetic - FA

PSO:

Particle swarm optimization

CS:

Cuckoo search

FPA:

Flower pollination algorithm

PFA:

Pathfinder algorithm

BBO:

Bio-geography based optimization

MCDM:

Multi-criteria decision making

TOPSIS:

Technique for order of preference by similarity to ideal solution

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gupta, D., Dhar, A.R. & Roy, S.S. A partition cum unification based genetic- firefly algorithm for single objective optimization. Sādhanā 46, 121 (2021). https://doi.org/10.1007/s12046-021-01641-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12046-021-01641-0

Keywords

Search

Navigation