Skip to main content
SpringerLink
Log in

Lie symmetries and invariant solutions of \((2+1)\)-dimensional breaking soliton equation

  • Published:
Pramana Aims and scope Submit manuscript

Abstract

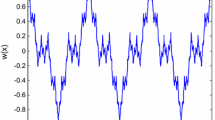
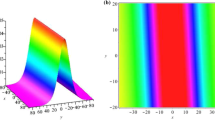
The present article deals with the symmetry reductions and invariant solutions of breaking soliton equation by virtue of similarity transformation method. The equation represents the collision of a Riemann wave propagating along the y-axis with a long wave along the x-axis. The infinitesimal transformations under one parameter for the governing system have been derived by exploiting the invariance property of Lie group theory. Consequently, the number of independent variables is reduced by one and the system remains invariant. A repeated application transforms the governing system into systems of ordinary differential equations. These systems degenerate well-known soliton solutions under some limiting conditions. The obtained solutions are extended with numerical simulation resulting in dark solitons, lumps, compactons, multisolitons, stationary and parabolic profiles and are shown graphically.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. F Calogero and A Degasperis, Nuovo Cimento B Ser. 11. 32, 201 (1976)

    Article  Google Scholar 

  2. G Q Xu, Appl. Math. Lett. 50, 16 (2015)

    Article  MathSciNet  Google Scholar 

  3. Y S Li and Y J Zhang, J Phys. A: Math. Gen. 26, 7487 (1993)

    Article  ADS  Google Scholar 

  4. H Y Ruan, J. Phys. Soc. Jpn. 71(2), 453 (2002)

    Article  ADS  Google Scholar 

  5. S H Ma, J Y Qiang and J P Fang, Commun. Theor. Phys. 48, 662 (2007)

    Article  ADS  Google Scholar 

  6. Y Chen, B Li and H Q Zhang, Commun. Theor. Phys. (Beijing, China) 40, 137 (2003)

    ADS  Google Scholar 

  7. Y Z Peng and E V Krishnan, Commun. Theor. Phys. (Beijing, China) 44, 807 (2005)

    Article  ADS  Google Scholar 

  8. Z Xie and H Q Zhang, Commun. Theor. Phys. (Beijing, China) 43, 401 (2005)

    ADS  Google Scholar 

  9. L N Cao, D S Wang and L X Chen, Commun. Theor. Phys. (Beijing, China) 47, 270 (2007)

    ADS  Google Scholar 

  10. S Zhang, Appl. Math. Comput. 190(1), 510 (2007)

    MathSciNet  Google Scholar 

  11. Z Zhao, Z Dai and G Mu, Comput. Math. Appl. 61(8), 2048 (2011)

    Article  MathSciNet  Google Scholar 

  12. F Taşcan and A Bekir, Appl. Math. Comput. 215(8), 3134 (2009)

    MathSciNet  Google Scholar 

  13. M Kumar, D V Tanwar and R Kumar, Comput. Math. Appl. 75(1), 218 (2018)

    Article  MathSciNet  Google Scholar 

  14. G W Bluman and J D Cole, Similarity methods for differential equations (Springer-Verlag, New York, 1974)

    Book  MATH  Google Scholar 

  15. P J Olver, Applications of Lie groups to differential equations (Springer-Verlag, New York, 1993)

    Book  MATH  Google Scholar 

  16. M Kumar and Y K Gupta, Pramana – J. Phys. 74(6), 883 (2010)

    Article  ADS  Google Scholar 

  17. M Kumar, D V Tanwar and R Kumar, Nonlinear Dyn. 94(4), 2547 (2018)

    Article  Google Scholar 

  18. M Kumar and D V Tanwar, Commun. Nonlinear Sci. Numer. Simul. 69, 45 (2019)

    Article  ADS  MathSciNet  Google Scholar 

  19. T Özer, Comput. Math. Appl. 55(9), 1923 (2008)

    Article  MathSciNet  Google Scholar 

  20. Y Yıldırım and E Yaşar, Chaos Solitons Fractals 107, 146 (2018)

    Article  ADS  MathSciNet  Google Scholar 

  21. T Raja Sekhar and P Satapathy, Comput. Math. Appl. 72(5), 1436 (2016)

    Article  MathSciNet  Google Scholar 

  22. A Bansal, A Biswas, Q Zhou and M M Babatin, Optik 169, 12 (2018)

    Article  ADS  Google Scholar 

  23. M Kumar and D V Tanwar, Comput. Math. Appl.76(11–12), 2535 (2018)

    Article  MathSciNet  Google Scholar 

  24. S S Ray, Comput. Math. Appl. 74(6), 1158 (2017)

    Article  MathSciNet  Google Scholar 

  25. M Singh and R K Gupta, Pramana – J. Phys. 92: 1 (2019)

    Article  ADS  Google Scholar 

  26. Abdullah, A R Seadawy and J Wang, Pramana – J. Phys. 91: 26 (2018)

  27. Z Du, B Tian, X Y Xie, J Chai and X Y Wu, Pramana – J. Phys. 90: 45 (2018)

    Article  ADS  Google Scholar 

  28. J Manafian and M Lakestani, Pramana – J. Phys. 92: 41 (2019)

    Article  ADS  Google Scholar 

  29. M Shahriari and J Manafian, Pramana – J. Phys. 93: 3 (2019)

    Article  ADS  Google Scholar 

  30. J Manafian, B M Ivatloo and M Abapour, Appl. Math. Comput. 356, 13 (2019)

    MathSciNet  Google Scholar 

  31. J Manafian, Comput. Math. Appl. 76(5), 1246 (2018)

    Article  MathSciNet  Google Scholar 

  32. J Manafian, M Lakestani and A Bekir, Pramana – J. Phys. 87: 95 (2016)

    Article  ADS  Google Scholar 

  33. M Cinefra, Int. J. Hydromechatronics 1(4), 415 (2019)

    Article  Google Scholar 

  34. T Ak, T Aydemir, A Saha and A H Kara, Pramana – J. Phys. 90: 78 (2018)

    Article  ADS  Google Scholar 

  35. A R Adem, Y Yıldırım and E Yaşar, Pramana – J. Phys. 92: 36 (2019)

    Article  ADS  Google Scholar 

  36. O I Bogoyavlenskii, Math. USSR Izvestiya 34(2), 245 (1989)

    Article  ADS  Google Scholar 

  37. N J Zabusky and M D Kruskal, Phys. Rev. Lett. 15, 240 (1965)

    Article  ADS  Google Scholar 

  38. A S Davydov, Phys. Scr. 20, 387 (1979)

    Article  ADS  Google Scholar 

  39. E Demler and A Maltsev, Ann. Phys. 326(7), 1775 (2011)

    Article  ADS  Google Scholar 

  40. D Daghan and O Donmez, Braz. J. Phys. 46(3), 321 (2016)

    Article  ADS  Google Scholar 

  41. M M Scott, M P Kostylev, B A Kalinikos and C E Patton, Phys. Rev. B 71, 174440(1–4) (2005)

    Article  ADS  Google Scholar 

  42. P Rosenau and J M Hyman, Phys. Rev. Lett. 70, 564 (1993)

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Motilal Nehru National Institute of Technology Allahabad, Prayagraj, 211 004, India

    Mukesh Kumar & Dig Vijay Tanwar

Authors
  1. Mukesh Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Dig Vijay Tanwar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Dig Vijay Tanwar.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kumar, M., Tanwar, D.V. Lie symmetries and invariant solutions of \((2+1)\)-dimensional breaking soliton equation. Pramana - J Phys 94, 23 (2020). https://doi.org/10.1007/s12043-019-1885-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12043-019-1885-1

Keywords

PACS

Search

Navigation