Skip to main content
SpringerLink
Log in

Lumps and rouge waves for a \((3+1)\)-dimensional variable-coefficient Kadomtsev–Petviashvili equation in fluid mechanics

  • Published:
Pramana Aims and scope Submit manuscript

Abstract

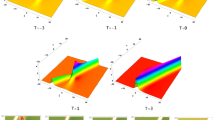
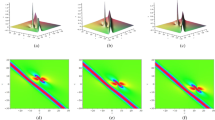
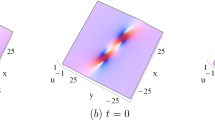
In this paper, a \((3+1)\)-dimensional variable-coefficient Kadomtsev–Petviashvili equation, which describes the long water waves and small-amplitude surface waves with the weak nonlinearity, weak dispersion and weak perturbation in fluid mechanics, is investigated. Lump, lump–soliton and rouge–soliton solutions are obtained with the aid of symbolic computation. For the lump and soliton, amplitudes are related to the nonlinearity coefficient and dispersion coefficient, while velocities are related to the perturbation coefficients. Fusion and fission phenomena between the lump and soliton are observed, respectively. Graphic analysis shows that: (i) soliton’s amplitude becomes larger after the fusion interaction, and becomes smaller after the fission interaction; (ii) after the interaction, the soliton propagates along the opposite direction to before when any one of the perturbation coefficients is a time-dependent function. For the interactions between the rogue wave and two solitons, the rogue wave splits from one soliton and merges into the other one, and the two solitons exchange the amplitudes through the energy transfer by the rogue wave.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. M J Ablowitz, D J Kaup, A C Newell and H Segur, Phys. Rev. Lett. 30, 1262 (2015)

    Article  ADS  Google Scholar 

  2. L Salasnich, Phys. Rev. Lett. 118, 130402 (2017) J J Su and Y T Gao, Superlattice. Microstruct. 120, 697 (2018)

  3. W Q Hu, Y T Gao, Z Z Lan, C Q Su and Y J Feng, Appl. Math. Model. 46, 126 (2017)

    Article  MathSciNet  Google Scholar 

  4. T Xu, C J Liu, F H Qi, C X Li and D X Meng, J. Nonlinear Math. Phys. 24, 116 (2017) Y J Feng, Y T Gao and X Yu, Nonlinear Dyn. 91, 29 (2018).

  5. M V Sorokin, V I Dubinko and V A Borodin, Phys. Rev. E 95, 012801 (2017)

    Article  ADS  MathSciNet  Google Scholar 

  6. X Y Xie and G Q Meng, Chaos Solitons Fractals 107, 143 (2018); T T Jia, Y Z Chai and H Q Hao, Superlattice. Microstruct. 105, 172 (2017)

  7. N J Zabusky and M D Kruskal, Phys. Rev. Lett. 15, 240 (1965)

    Article  ADS  Google Scholar 

  8. M J Ablowitz and P A Claarkson, Solitons, nonlinear evolution equations and inverse scattering (Cambridge University Press, New York, 1991)

    Book  Google Scholar 

  9. W M Moslem, S Ali, P K Shukla, X Y Tang and G Rowlands, Phys. Plasmas 14, 082308 (2007)

    Article  ADS  Google Scholar 

  10. B M Herbst and M J Ablowitz, Phys. Rev. Lett. 62, 2065 (1989)

    Article  ADS  MathSciNet  Google Scholar 

  11. D Nath and P Roy, Phys. Rev. Lett. 14, 347 (2017)

    Google Scholar 

  12. A Lekomtsev and V Pimenov, Appl. Math. Comput. 256, 83 (2015) X Y Gao, Appl. Math. Lett. 73, 143 (2017)

  13. Z Z Lan, Y T Gao, J W Yang, C Q Su and B Q Mao, Commun. Nonlinear Sci. Numer. Simul. 44, 360 (2017)

    Article  ADS  MathSciNet  Google Scholar 

  14. R Grimshaw, Stud. Appl. Math. 134, 363 (2015) J J Su and Y T Gao, Eur. Phys. J. Plus 133, 96 (2018)

  15. X Y Xie and Z H Yan, Appl. Math. Lett. 80, 48 (2018) G F Deng and Y T Gao, Superlattice. Microstruct. 109, 345 (2017)

  16. M Li, T Xu, L Wang and F H Qi, Appl. Math. Lett. 60, 8 (2016) Q M Huang, Y T Gao, S L Jia, Y L Wang and G F Deng, Nonlinear Dyn. 87, 2529 (2017)

  17. P A Clarkson, IMA J. Appl. Math. 44, 27 (1990) X Y Gao, Ocean Engineering 96, 245 (2015)

  18. R M Elshiekh, Z. Naturf. A 70, 445 (2015)

  19. K Porsezian and R V J Raja, Pramana – J. Phys. 85, 993 (2015)

    Google Scholar 

  20. D H Peregrine, J. Aust. Math. Soc. Ser. B 25, 16 (1983)

  21. J Villarroel, J Prada and P G Estevez, Stud. Appl. Math. 122, 395 (2009)

    Article  MathSciNet  Google Scholar 

  22. Y K Liu and L I Biao, Pramana – J. Phys. 88: 57 (2017)

    Google Scholar 

  23. X Lü and W X Ma, Nonlinear Dyn. 85, 1217 (2016)

    Article  Google Scholar 

  24. J B Zhang and W X Ma, Comput. Math. Appl. 74, 591 (2017) P Jin, C A Bouman and K D Sauer, IEEE Trans. Comput. Imaging 1, 200 (2015)

  25. B Simon, B Carsten and V Ivan, Sci. Rep. 6, 35207 (2016) G F Deng and Y T Gao, Eur. Phys. J. Plus 132, 255 (2017)

  26. H Q Zhao and W X Ma, Comput. Math. Appl. 74, 1399 (2017) Q M Huang and Y T Gao, Nonlinear Dyn. 89, 2855 (2017)

  27. M S Khatun, M F Hoque and M A Rahman, Pramana – J. Phys. 88: 86 (2017)

    Google Scholar 

  28. J Y Yang, W X Ma and Z Qin, Anal. Math. Phys. 1, 1 (2017)

    Google Scholar 

  29. W X Ma, X Yong and H Q Zhang, Comput. Math. Appl. (2017) (in press) Q M Huang and Y T Gao, Nonlinear Dyn. 89, 2855 (2017)

  30. J Chai, B Tian, W R Sun and X Y Xie, Comput. Math. Appl. 71, 2060 (2016)

    Article  MathSciNet  Google Scholar 

  31. H M Jaradt, S Al-Shara, F Awawdeh and M Alquran, Phys. Scr. 85, 035001 (2012)

    Article  ADS  Google Scholar 

  32. J Chai, B Tian, X Y Wu and L Liu, Eur. Phys. J. Plus 132, 60 (2017)

    Article  Google Scholar 

  33. R Hirota, The direct method in soliton theory (Cambridge University Press, Cambridge, 2004)

    Book  MATH  Google Scholar 

  34. X Zhang and Y Chen, Commun. Nonlinear Sci. Numer. Simul. 52, 24 (2017)

    Article  ADS  MathSciNet  Google Scholar 

  35. J Y Yang and W X Ma, Nonlinear Dyn. 1, 6 (2017)

    Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China under Grant Nos 11772017, 11272023 and 11471050, by the Fund of State Key Laboratory of Information Photonics and Optical Communications (Beijing University of Posts and Telecommunications), China (IPOC: 2017ZZ05), and by the Fundamental Research Funds for the Central Universities of China under Grant No. 2011BUPTYB02.

Author information

Authors and Affiliations

  1. State Key Laboratory of Information Photonics and Optical Communications, and School of Science, Beijing University of Posts and Telecommunications, Beijing, 100876, China

    Ying Yin, Bo Tian, Han-Peng Chai, Yu-Qiang Yuan & Zhong Du

Authors
  1. Ying Yin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Bo Tian
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Han-Peng Chai
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yu-Qiang Yuan
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Zhong Du
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Bo Tian.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yin, Y., Tian, B., Chai, HP. et al. Lumps and rouge waves for a \((3+1)\)-dimensional variable-coefficient Kadomtsev–Petviashvili equation in fluid mechanics. Pramana - J Phys 91, 43 (2018). https://doi.org/10.1007/s12043-018-1609-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12043-018-1609-y

Keywords

Search

Navigation