Abstract
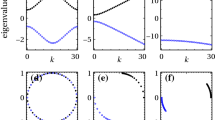
In this article we present an effective Hamiltonian approach for discrete time quantum random walk. A form of the Hamiltonian for one-dimensional quantum walk has been prescribed, utilizing the fact that Hamiltonians are generators of time translations. Then an attempt has been made to generalize the techniques to higher dimensions. We find that the Hamiltonian can be written as the sum of a Weyl Hamiltonian and a Dirac comb potential. The time evolution operator obtained from this prescribed Hamiltonian is in complete agreement with that of the standard approach. But in higher dimension we find that the time evolution operator is additive, instead of being multiplicative (see Chandrashekar, Sci. Rep. 3, 2829 (18)). We showed that in the case of two-step walk, the time evolution operator effectively can have multiplicative form. In the case of a square lattice, quantum walk has been studied computationally for different coins and the results for both the additive and the multiplicative approaches have been compared. Using the graphene Hamiltonian, the walk has been studied on a graphene lattice and we conclude the preference of additive approach over the multiplicative one.














Similar content being viewed by others
References
Y Aharonov, L Davidovich and N Zagury, Phys. Rev. A 48, 1687 (1993)
Patrici Molinàs-Mata, M A Muñoz, Daniel O Martínez and Albert-László Barabási, Phys. Rev. E 54, 968 (1996)
A Nayak and A Vishwanath, eprint arXiv:quant-ph/ 0010117 (2000)
Andris Ambainis, Eric Bach, Ashwin Nayak, Ashvin Vishwanath and John Watrous, One-dimensional quantum walks, in: Proceedings of the Thirty-third Annual ACM Symposium on Theory of Computing, STOC ’01, pp. 37–49, New York, NY, USA, ACM, ISBN: 1-58113-349-9 (2001)
J Kempe, Contemp. Phys. 44(4), 307 (2003)
Dorit Aharonov, Andris Ambainis, Julia Kempe and Umesh Vazirani, Quantum walks on graphs, in: Proceedings of the Thirty-third Annual ACM Symposium on Theory of Computing, STOC ’01, pp. 50–59, ACM (2001)
Julia Kempe, Prob. Theory Rel. Fields 133(2), 215 (2005), ISSN: 0178-8051
Ben Tregenna, Will Flanagan, Rik Maile and Viv Kendon, New J. Phys. 5(1), 83 (2003)
Edward Farhi and Sam Gutmann, Phys. Rev. A 58, 915 (1998)
Fugao Wang and D P Landau, Phys. Rev. Lett. 86, 2050 (2001)
Neil Shenvi, Julia Kempe and K Birgitta Whaley, Phys. Rev. A 67, 052307 (2003)
Andris Ambainis, Int. J. Quantum Inform. 1(4), 507 (2003)
Andrew M Childs, Richard Cleve, Enrico Deotto, Edward Farhi, Sam Gutmann and Daniel A Spielman, Exponential algorithmic speedup by a quantum walk, in: Proceedings of the Thirty-fifth Annual ACM Symposium on Theory of Computing, STOC ’03, pp. 59–68, ACM (2003)
Andrew M Childs, Phys. Rev. Lett. 102, 180501 (2009)
Meltem Gönülol, Ekrem Aydıner, Yutaka Shikano, and Özgür E Müstecaplıog͂lu, New J. Phys. 13(3), 033037 (2011)
M Štefaňák, T Kiss, and I Jex, Phys. Rev. A 78, 032306 (2008)
M Štefaňák, B Kollár, T Kiss, and I Jex, Phys. Scr. 2010(T140), 014035 (2010)
C M Chandrashekar, Sci. Rep. 3, 2829 (2013)
C A Ryan, M Laforest, J C Boileau, and R Laflamme, Phys. Rev. A 72, 062317 (2005)
Jiangfeng Du, Hui Li, Xiaodong Xu, Mingjun Shi, Jihui Wu, Xianyi Zhou, and Rongdian Han, Phys. Rev. A 67, 042316 (2003)
Michał Karski, Leonid Förster, Jai-Min Choi, Andreas Steffen, Wolfgang Alt, Dieter Meschede, and Artur Widera, Science 325(5937), 174 (2009)
H Schmitz, R Matjeschk, Ch Schneider, J Glueckert, M Enderlein, T Huber, and T Schaetz, Phys. Rev. Lett. 103, 090504 (2009)
F Zähringer, G Kirchmair, R Gerritsma, E Solano, R Blatt, and C F Roos, Phys. Rev. Lett. 104, 100503 (2010)
A Schreiber, K N Cassemiro, V Potoček, A Gábris, P J Mosley, E Andersson, I Jex, and Ch Silberhorn, Phys. Rev. Lett. 104, 050502 (2010)
Alberto Peruzzo, Mirko Lobino, Jonathan C F Matthews, Nobuyuki Matsuda, Alberto Politi, Konstantinos Poulios, Xiao-Qi Zhou, Yoav Lahini, Nur Ismail, Kerstin Wörhoff, Yaron Bromberg, Yaron Silberberg, Mark G Thompson, and Jeremy L OBrien, Science 329, 5998, 1500 (2010)
Iwo Bialynicki-Birula, Phys. Rev. D 49, 6920 (1994)
A T Schmitz and W A Schwalm, Phys. Lett. A 380, 1125 (2016)
D ben-Avraham, E Bollt, and C Tamon, eprint arXiv:cond-mat/0409514(2004)
A M Childs, Commun. Math. Phys. 294, 581 (2010)
A H Castro Neto, F Guinea, N M R Peres, K S Novoselov, and A K Geim, Rev. Mod. Phys. 81, 109 (2009)
In our convention, \(\mathbb {1}_n\) (where n∈N, the set of natural numbers) denotes n×n identity operator in finite-dimensional space, \(\mathbb {1}\) denotes infinite-dimensional identity operator acting on the space spanned by the coordinates of all the points in space and \(\mathcal {I}\) denotes infinite-dimensional identity operator such that \(\mathcal {I}=\mathbb {1}_n \otimes \mathbb {1}\).
At a first glance, eq. (12) may look like dimensionally inconsistent but it is not, because while converting a functional from its discrete to continuous form we must divide the discrete form with a weight factor of dimension the same as that of the continuous variable. In this expression we have used a weight factor of unit length.
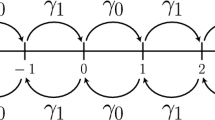
In the two-step approach if the particle moves along x-axis at one step, the next step must be along y-axis. So we can interpret the method as follows: first, W x operates on the particle and displaces it along x-direction. When it reaches the next lattice point, W y operates. So, in this case the time evolution operator is different at different lattice points. The total time evolution operator for the lattice is the sum of the time evolution operator at all the lattice points. If the particle starts to move along X direction from the point (0,0), at all the even points (points for which x + y is even) the operator W x will act while at all the odd points (points for which x + y is odd) the operator W y will act. Although the operator is not actually multiplicative, the net effect in two-step can be described by W y W x because after evolution by W x the particle would reach the next lattice point where the evolution is governed by W y . This can happen if at the points where W x is operating, k y v y =0 and at the points where W y is operating, k x v x =0. In this way, we can reproduce the two-step approach of ref. [18] starting from our Hamiltonian formulation of single-step walk.
Acknowledgements
NP acknowledges the financial support from the Council of Scientific and Industrial Research (CSIR), India as a SPM JRF. Thanks are also due to the Department of Physics, Indian Institute of Technology, Kanpur, as a significant amount of work was done when the authors were there.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Derivation of Hamiltonian from evolution operators in 1D
1.1 A.1 Derivation of H T
If the Hamiltonian corresponding to T is defined as \(H_{T} \otimes \mathbb {1}\), then it can be derived as follows:
Thus, we see that the derived Hamiltonian \(H_{T} \otimes \mathbb {1}\) is Hermitian.
Let us find the expression for H T now. Taking projection onto x-space we get
1.2 A.2 Derivation of H S
If we denote the Hamiltonian governing the chirality flip as \({\sum }_{m} H_{S} \otimes \vert m \rangle \langle m \vert \), we can write
Now H S is Hermitian by construction, because every unitary operator on a Hilbert space can be written as U=eiA for some Hermitian A.
1.3 A.3 Derivation of H(x)
The total Hamiltonian H is given by
Therefore, by taking projection over x-space we get
Here in the second step we have used a proper unit weighting factor.
Appendix B: Derivation of evolution operator from Hamiltonian in 2D square lattice
We have
Now following the logic as described in §3.1.1, we can say that [H S ,H T ] Δt=0. Now,
Again,
Therefore,
Therefore, we have
Rights and permissions
About this article
Cite this article
SARKAR, D., PAUL, N., BHATTACHARYA, K. et al. An effective Hamiltonian approach to quantum random walk. Pramana - J Phys 88, 45 (2017). https://doi.org/10.1007/s12043-016-1340-5
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12043-016-1340-5