Skip to main content
SpringerLink
Log in

Finite element modeling of two-directional FGM beams under hygrothermal effect

  • Original Paper
  • Published:
International Journal on Interactive Design and Manufacturing (IJIDeM) Aims and scope Submit manuscript

Abstract

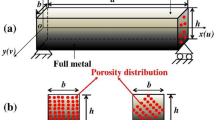
This investigation describes the computational characteristics of two-directional functionally graded beams under the hygrothermal effect. A prismatic two-directional functionally graded beam (FGM) is used in this work. Temperature and moisture are applied to this FGM beam. Stainless steel (SUS304) and silicon nitride (Si3N4) are the materials used in their construction. Finite element method (FEM) software calculates the eigenfrequencies of two-directional FGM (COMSOL Multiphysics). The power law governs the material properties. The Euler–Bernoulli beam theory (EBT) is used in this study. The mechanical parameters are varied in longitudinal and transverse directions. The eigenfrequencies of two-directional FGM beams are affected by the material gradient parameter, the boundary condition, and the aspect ratio under the influence of the hygrothermal effect. The results obtained for reduced cases are used to validate the results computed with the FEM. The natural frequencies decrease with increased moisture concentration and temperature variation under clamped–clamped (C–C) boundary conditions and increase under clamped-free (C–F) boundary conditions. It is also observed that natural frequencies increase with the increase in material gradient parameters in the z-direction (nz) and decrease with the increase in material gradient parameters in the x-direction (nx) under C–C and C–F end conditions. With the increase in aspect ratio, the natural frequency increases under C–C and C–F boundary conditions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Aria, A.I., Friswell, M.I.: A nonlocal finite element model for buckling and vibration of functionally graded nanobeams. Compos. B Eng. 1(166), 233–246 (2019)

    Article  Google Scholar 

  2. Wang, Y., Ren, H., Fu, T., Shi, C.: Hygrothermal mechanical behaviors of axially functionally graded microbeams using a refined first order shear deformation theory. Acta Astronaut. 1(166), 306–316 (2020)

    Article  Google Scholar 

  3. Nguyen, T.K., Nguyen, B.D., Vo, T.P., et al.: Hygro-thermal effects on vibration and thermal buckling behaviors of functionally graded beams. Compos. Struct. 176, 1050–1060 (2017)

    Article  Google Scholar 

  4. Rajasekaran, S., Tochaei, E.N.: Free vibration analysis of axially functionally graded tapered Timoshenko beams using differential transformation element method and differential quadrature element method of lowest-order. Meccanica 49(4), 995–1009 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  5. Sharma, P., Singh, R., Hussain, M.: On modal analysis of axially functionally graded material beam under hygrothermal effect. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 234(5), 1085–1101 (2020)

    Article  Google Scholar 

  6. Chen, W.R., Chang, H.: Vibration analysis of bidirectional functionally graded Timoshenko beams using Chebyshev collocation method. Int. J. Struct. Stab. Dyn. 21(01), 2150009 (2021)

    Article  MathSciNet  Google Scholar 

  7. Karamanl, A.: Free vibration analysis of two directional functionally graded beams using a third order shear deformation theory. Compos. Struct. 1(189), 127–136 (2018)

    Article  Google Scholar 

  8. Trinh, L.C., Vo, T.P., Thai, H.T., Nguyen, T.K.: Size-dependent vibration of bi-directional functionally graded microbeams with arbitrary boundary conditions. Compos. B Eng. 1(134), 225–245 (2018)

    Article  Google Scholar 

  9. Gupta, B., Sharma, P., Rathore, S.K.: A new numerical modeling of an axially functionally graded piezoelectric beam. J. Vib. Eng. Technol. 13, 1–6 (2022)

    Google Scholar 

  10. Sharma, P., Gupta, B., Rathore, S.K., Khinchi, A., Gautam, M.: Computational characteristics of an exponentially functionally graded piezoelectric beam. Int. J. Interact. Des. Manuf. (IJIDeM) 31, 1–7 (2022)

    Google Scholar 

  11. Parashar, S.K., Sharma, P.: Modal analysis of shear-induced flexural vibration of FGPM beam using Generalized Differential Quadrature method. Compos. Struct. 139, 222–232 (2016)

    Article  Google Scholar 

  12. Sharma, P., Parashar, S.K.: Free vibration analysis of shear-induced flexural vibration of FGPM annular plate using generalized differential quadrature method. Compos. Struct. 1(155), 213–222 (2016)

    Article  Google Scholar 

  13. Sharma, P.: Efficacy of Harmonic Differential Quadrature method to vibration analysis of FGPM beam. Compos. Struct. 1(189), 107–116 (2018)

    Article  Google Scholar 

  14. Sharma, P.: Vibration Analysis of Functionally Graded Piezoelectric Actuators. Springer, New York (2019)

    Book  Google Scholar 

  15. Singh, R., Sharma, P.: Vibration analysis of an axially functionally graded material non prismatic beam under axial thermal variation in humid environment. J. Vib. Control 28(23–24), 3608–3621 (2021)

    Article  MathSciNet  Google Scholar 

  16. Sharma, P., Gautam, M., Chaturvedi, M.: Vibration analysis of EFGM beam using GDQ method. Int. J. Interact. Des. Manuf. (IJIDeM) 26, 1–9 (2022)

    Google Scholar 

  17. Mohammadnejad, M.: Free vibration analysis of axially functionally graded beams using Fredholm integral equations. Arch. Appl. Mech. 5, 1–6 (2022)

    Google Scholar 

  18. Zghal, S., Ataoui, D., Dammak, F.: Free vibration analysis of porous beams with gradually varying mechanical properties. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 236(3), 800–812 (2022)

    Google Scholar 

  19. Balireddy, S.N., Pitchaimani, J.: Stability and dynamic behaviour of bi-directional functionally graded beam subjected to variable axial load. Mater. Today Commun. 1(32), 104043 (2022)

    Article  Google Scholar 

  20. Nejad, M.Z., Hadi, A.: Non-local analysis of free vibration of bi-directional functionally graded Euler–Bernoulli nano-beams. Int. J. Eng. Sci. 1(105), 1–1 (2016)

    MathSciNet  MATH  Google Scholar 

  21. Sharma, P., Kataria, S.D., Khinchi, A.: On modal analysis of bi-direction FGM beam under general end conditions. Mater. Today Proc. 1(44), 1853–1856 (2021)

    Article  Google Scholar 

  22. Sharma, P., Khinchi, A.: On frequency investigation of bi-directional FGM beam under thermal effect. Mater. Today Proc. 1(47), 6089–6092 (2021)

    Article  Google Scholar 

  23. Khinchi, A., Sharma, P.: A convergence behavior of HDQ and GDQ methods to analyze vibration characteristics of different configurations of FGM beams. Mater. Today: Proc. 62, 2670–3674 (2022)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Rajasthan Technical University Kota, Kota, India

    Pankaj Sharma & Ashish Khinchi

Authors
  1. Pankaj Sharma
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ashish Khinchi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Pankaj Sharma.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sharma, P., Khinchi, A. Finite element modeling of two-directional FGM beams under hygrothermal effect. Int J Interact Des Manuf (2023). https://doi.org/10.1007/s12008-022-01190-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12008-022-01190-8

Keywords

Search

Navigation