Skip to main content
SpringerLink
Log in

Periodic representations in Salem bases

  • Published:
Israel Journal of Mathematics Aims and scope Submit manuscript

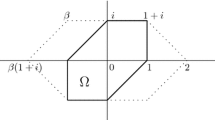
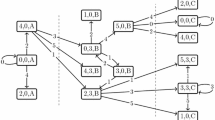
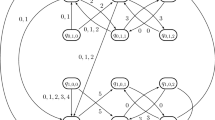
Abstract

We prove that all algebraic bases β allow an eventually periodic representation of the elements of ℚ(β) with a finite alphabet of digits \({\cal A}\). Moreover, the classification of bases allowing that those representations have the socalled weak greedy property is given.

The decision problem whether a given pair (β, \({\cal A}\)) allows eventually periodic representations proves to be rather hard, for it is equivalent to a topological property of the attractor of an iterated function system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. S. Akiyama, T. Borbély, H. Brunotte, A. Pethő and J. M. Thuswaldner, Generalized radix representations and dynamical systems. I, Acta Mathematica Hungarica 108 (2005), 207–238.

    Article  MathSciNet  Google Scholar 

  2. S. Akiyama, J. M. Thuswaldner and T. Zaïmi, Characterisation of the numbers which satisfy the height reducing property, Koninklijke Nederlandse Akademie van Wetenschappen. Indagationes Mathematicae 26 (2015), 24–27.

    MathSciNet  MATH  Google Scholar 

  3. S. Baker, Z. Masáková, E. Pelantová and T. Vávra, On periodic representations in non-Pisot bases, Monatshefte für Mathematik 184 (2017), 1–19.

    Article  MathSciNet  Google Scholar 

  4. D. W. Boyd, Salem numbers of degree four have periodic expansions, in Théorie des nombres (Quebec, PQ, 1987), de Gruyter, Berlin, 1989, pp. 57–64.

    Google Scholar 

  5. D. W. Boyd, On the beta expansion for Salem numbers of degree 6, Mathematics of Computation 65 (1996), 861–875.

    Article  MathSciNet  Google Scholar 

  6. M. Brzicová, C. Frougny, E. Pelantová and M. Svobodová, On-line multiplication and division in real and complex bases, in 2016 IEEE 23rd Symposium on Computer Arithmetic (ARITH), IEEE, Los Alamitos, CA, 2015, pp. 134–141.

    Google Scholar 

  7. Y. Bugeaud, On a property of Pisot numbers and related questions, Acta Mathematica Hungarica 73 (1996), 33–39.

    Article  MathSciNet  Google Scholar 

  8. P. Erdös, I. Joó and V. Komornik, Characterization of the unique expansions \(1 = \sum\nolimits_{i = 1}^\infty {{q^{-{n_i}}}} \) and related problems, Bulletin de la Société Mathématique de France 118 (1990), 377–390.

    Article  MathSciNet  Google Scholar 

  9. D.-J. Feng, On the topology of polynomials with bounded integer coefficients, Journal of the European Mathematical Society 18 (2016), 181–193.

    Article  MathSciNet  Google Scholar 

  10. K. G. Hare, The structure of the spectra of Pisot numbers, Journal of Number Theory 105 (2004), 262–274.

    Article  MathSciNet  Google Scholar 

  11. K. G. Hare, Z. Masáková and T. Vávra, On the spectra of Pisot-cyclotomic numbers, Letters in Mathematical Physics 108 (2018), 1729–1756.

    Article  MathSciNet  Google Scholar 

  12. T. Hejda and E. Pelantová, Spectral properties of cubic complex Pisot units, Mathematics of Computation 85 (2016), 401–421.

    Article  MathSciNet  Google Scholar 

  13. J. E. Hutchinson, Fractals and self-similarity, Indiana University Mathematics Journal 30 (1981), 713–747.

    Article  MathSciNet  Google Scholar 

  14. V. Kala and T. Vávra, Periodic representations in algebraic bases, Monatshefte für Mathematik 188 (2019), 109–119.

    Article  MathSciNet  Google Scholar 

  15. Z. Masáková, K. Pastirčáková and E. Pelantová, Description of spectra of quadratic Pisot units, Journal of Number Theory 150 (2015), 168–190.

    Article  MathSciNet  Google Scholar 

  16. M. Minervino and J. Thuswaldner, The geometry of non-unit Pisot substitutions, Université de Grenoble. Annales de l’Institut Fourier 64 (2014), 1373–1417.

    Article  MathSciNet  Google Scholar 

  17. J. Neukirch, Algebraic Number Theory, Grundlehren der Mathematischen Wissenschaften, Vol. 322, Springer, Berlin, 1999.

    Google Scholar 

  18. A. Rényi, Representations for real numbers and their ergodic properties, Acta Mathematica. Academiae Scientiarum Hungaricae 8 (1957), 477–493.

    Article  MathSciNet  Google Scholar 

  19. K. Schmidt, On periodic expansions of Pisot numbers and Salem numbers, Bulletin of the London Mathematical Society 12 (1980), 269–278.

    Article  MathSciNet  Google Scholar 

  20. J. Šíma and P. Savický, Quasi-periodic β-expansions and cut languages, Theoretical Computer Science 720 (2018), 1–23.

    Article  MathSciNet  Google Scholar 

  21. W. Steiner and J. M. Thuswaldner, Rational self-affine tiles, Transactions of the American Mathematical Society 367 (2015), 7863–7894.

    Article  MathSciNet  Google Scholar 

  22. W. P. Thurston, Groups, tilings and finite state automata Research report, Geometry Computing Group, AMS colloquium lectures, Minneapolis, MN, 1989.

    Google Scholar 

  23. T. Zaïmi, On an approximation property of Pisot numbers. II, Journal de Théorie des Nombres de Bordeaux 16 (2004), 239–249.

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The author thanks the anonymous reviewer for many useful comments.

This work has been supported by Czech Science Foundation GAČR, grant 17-04703Y, and by Charles University Research Centre program No. UNCE/SCI/022.

Author information

Authors and Affiliations

  1. Department of Algebra, Charles University, Sokolovská 83, 186 75, Praha 8, Czech Republic

    Tomáš Vávra

Authors
  1. Tomáš Vávra
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tomáš Vávra.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Vávra, T. Periodic representations in Salem bases. Isr. J. Math. 242, 83–95 (2021). https://doi.org/10.1007/s11856-021-2123-3

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11856-021-2123-3

Search

Navigation