Abstract
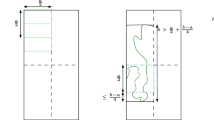
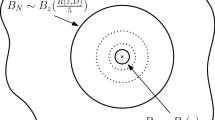
The Rohde–Schramm theorem states that Schramm–Loewner Evolution with parameter κ (or SLEκ for short) exists as a random curve, almost surely, if κ ≠ 8. Here we give a new and concise proof of the result, based on the Liouville quantum gravity coupling (or reverse coupling) with a Gaussian free field. This transforms the problem of estimating the derivative of the Loewner flow into estimating certain correlated Gaussian free fields. While the correlation between these fields is not easy to understand, a surprisingly simple argument allows us to recover a derivative exponent first obtained by Rohde and Schramm [14], subsequently shown to be optimal by Lawler and Viklund [17], which then implies the Rohde–Schramm theorem.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
L. V. Ahlfors, Complex Analysis. An Introduction to the Theory of Analytic Functions of One Complex Variable, McGraw-Hill, New York–Toronto–London, 1953.
N. Berestycki, Introduction to the Gaussian free field and Liouville quantum gravity, http://www.statslab.cam.ac.uk/~beresty/Articles/oxford4.pdf.
N. Berestycki and J. R. Norris, Lectures on Schramm–Loewner Evolution, (2011).
R. Courant and D. Hilbert, Methods of Mathematical Physics. Vol. I, Interscience, New York, 1953.
P. K. Friz and A. Shekhar, On the existence of SLE trace: finite energy drivers and non-constant κ, Probability Theory and Related Fields 169 (2017), 353–376.
E. Gwynne, J. Miller and X. Sun, Almost sure multifractal spectrum of Schramm–Loewner evolution, Duke Mathematical Journal 167 (2018), 1099–1237.
I. Karatzas and S. Shreve, Brownian Motion and Stochastic Calculus, Graduate Texts in Mathematics, Vol. 113, Springer, New York, 1991.
G. F. Lawler, Conformally Invariant Processes in the Plane, Mathematical Surveys and Monographs, Vol. 114, American Mathematical Society, Providence, RI, 2005.
G. F. Lawler, O. Schramm and W. Werner, Conformal invariance of planar loop-erased random walks and uniform spanning trees, Annals of Probability 32 (2004), 939–995.
J. R. Lind, A sharp condition for the Loewner equation to generate slits, Annales Academiae Scientiarum Fennicae. Series A1. Mathematica 30 (2005), 143–158.
D. E. Marshall and S. Rohde, The Loewner differential equation and slit mappings, Journal of the American Mathematical Society 18 (2005), 763–778.
J. Miller and S. Sheffield, Quantum Loewner evolution, Duke Mathematical Journal 165 (2016), 3241–3378.
J. Miller and S. Sheffield, Liouville quantum gravity and the Brownian map II: geodesics and continuity of the embedding, preprint, arXiv:1605.03563.
S. Rohde and O. Schramm, Basic properties of SLE, Annals of Mathematics 161 (2005), 883–924.
S. Rohde, H. Tran and M. Zinsmeister, The Loewner equation and Lipschitz graphs, Revista Matemática Iberoamericana 34 (2018), 937–948.
S. Sheffield, Conformal weldings of random surfaces: SLE and the quantum gravity zipper, Annals of Probability 44 (2016), 3474–3545.
F. Viklund and G. F. Lawler, Almost sure multifractal spectrum for the tip of an SLE curve, Acta Mathematica 209 (2012), 265–322.
T. Yamada, On a comparison theorem for solutions of stochastic differential equations and its applications, Journal of Mathematics of Kyoto University 13 (1973), 497–512.
Author information
Authors and Affiliations
Corresponding author
Additional information
The first author’s research was supported in part by EPSRC grants EP/L018896/1 and EP/I03372X/1.
The second author was a PhD student while this work was taking place, funded by EPSRC grant EP/H023348/1.
Rights and permissions
About this article
Cite this article
Berestycki, N., Jackson, H. The Rohde–Schramm theorem via the Gaussian free field. Isr. J. Math. 228, 973–999 (2018). https://doi.org/10.1007/s11856-018-1789-7
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11856-018-1789-7